Bilayer-Spanning DNA Nanopores with Voltage-Switching between Open and Closed State

Abstract

Membrane-spanning nanopores from folded DNA are a recent example of biomimetic man-made nanostructures that can open up applications in biosensing, drug delivery, and nanofluidics. In this report, we generate a DNA nanopore based on the archetypal six-helix-bundle architecture and systematically characterize it via single-channel current recordings to address several fundamental scientific questions in this emerging field. We establish that the DNA pores exhibit two voltage-dependent conductance states. Low transmembrane voltages favor a stable high-conductance level, which corresponds to an unobstructed DNA pore. The expected inner width of the open channel is confirmed by measuring the conductance change as a function of poly(ethylene glycol) (PEG) size, whereby smaller PEGs are assumed to enter the pore. PEG sizing also clarifies that the main ion-conducting path runs through the membrane-spanning channel lumen as opposed to any proposed gap between the outer pore wall and the lipid bilayer. At higher voltages, the channel shows a main low-conductance state probably caused by electric-field-induced changes of the DNA pore in its conformation or orientation. This voltage-dependent switching between the open and closed states is observed with planar lipid bilayers as well as bilayers mounted on glass nanopipettes. These findings settle a discrepancy between two previously published conductances. By systematically exploring a large space of parameters and answering key questions, our report supports the development of DNA nanopores for nanobiotechnology.

Building rationally designed nanoscale porous structures that mediate transport across membranes is of general interest in fundamental and applied science.^1,2 Biomimetic engineered nanopores³ that insert into lipid bilayers are of particular relevance for biorelated applications⁴ including biosensing. In nanopore analytics, single molecules passing or binding to a nanopore are detected by the associated modulations in ionic current.^5,2,6−10 The approach has gained popularity due to its simplicity, the wide range of accessible analytes,⁶ and the ability to sequence DNA in a label-free fashion.¹¹⁻¹⁴ The sensing of large analytes such as proteins has been achieved with dedicated approaches¹⁵⁻¹⁸ and also solid-state nanopores.^6,19−21 Membrane nanopores are also of interest as research tools in cell biology to regulate ionic flux²² or in synthetic biology to interconnect cells or proto-cells within artificial tissues.²³ All of these applications rely on engineered pores with tailored dimensions and defined conductance properties.

Engineered or synthetic nanopores can be made from peptides and proteins, but also with organic molecules or polymers²⁴⁻²⁹ aided by modeling and simulations.³⁰ The most recent invention is membrane-spanning channels composed of folded and structurally defined DNA. Predated by nanofunnels³¹ and nanoplates with an embedded hole,³² DNA origami channels carry hydrophobic lipid anchors to overcome the energetic cost of placing negatively charged DNA structures into the hydrophobic lipid bilayer.³³⁻³⁵ As lipid anchors, cholesterol,³³ charge-neutralized phosphate analogues in the DNA backbone,^34,36 and porphyrin³⁵ have been used. The latter is remarkable, as only two separate anchors were required to embed the negatively charged DNA nanopores into the bilayer.³⁵ The principle of DNA pores has been independently demonstrated with channels of 42 nm length by Langecker etal.³³ and 14 nm by Burns etal.³⁴ Irrespective of their size, the nominal width of both channels was 2 nm. Their nanoscale architecture also followed the same common honeycomb design based on DNA origami.^37,38 Accordingly, the central channel was surrounded by six hexagonally arranged DNA duplexes that were interconnected by DNA crossovers. However, the larger pore was formed from a long DNA scaffold and multiple staple oligonucleotides,³³ while the shorter version was assembled solely from oligonucleotides.^34,35 The latter approach previously used for other small nanostructures^39,40 benefits from the ease of fabrication, lower synthesis costs, and the production of larger amounts of pores at higher concentration.

DNA nanopores have been characterized in previous studies in terms of assembly, structure, and conductance,³³⁻³⁵ but several important questions related to the inner channel dimensions and conductance properties remain unresolved. Comprehensive single-channel current analysis is important as it can—in general terms—help distinguish the static and dynamic heterogeneity of samples and probe the channels’ internal structure and properties. In order to advance the field, this report aims to address and settle the following fundamental scientific points about DNA nanopores. At a basic level, (i) it has not been proven that the channels assume the theoretically predicted inner width of 2 nm once embedded inside the bilayer. Conventionally, dimensions of stable membrane-embedded pores are indirectly validated by comparing the experimental conductance values with the theoretical values calculated from the assumed dimensions. In the case of DNA nanopores, the calculations are not suitable because the simple model does not account for the ion permeable⁴¹ and structurally dynamic⁴² pore wall. Independent of any model, direct experimental proof such as size-dependent blocking with probe molecules is probably most suited to determine the pore dimensions.

We (ii) lack a fundamental understanding of whether ions indeed flow predominantly inside the section of the channel that spans the lipid bilayer. In a proposed alternative, ions might pass outside the DNA pore through the locally disrupted lipid bilayer membrane. A gap between the outer pore wall and an curved lipid bilayer has been proposed to account for the fact that hydrophobic lipid chains cannot be close to the negatively charged DNA nanopore.³³

Another important point to be clarified is (iii) the discrepancy between the measured conductance values of the known pores.^33,34 All published DNA nanochannels follow the six-duplex-bundle design with the same nominal channel diameter. Hence, their pore currents should depend—as a first approximation—solely on the channel height, given the inverse dependence of conductance on conductor length. Yet, contrary to the expectation that a shorter channel should yield a higher current, the conductance for the 14 nm pore of Burns etal. with a value of 0.25–0.4 nS^34,35 is smaller than the value of 0.89 ± 0.15 nS for the 42 nm origami pore of Langecker etal.³³

Finally, (iv) DNA pores have been analyzed with different lipid bilayer systems, which might influence the conductance values and could account for the discrepancy. In the case of Langecker etal.,³³ the nanostructures were examined with planar lipid bilayer recordings, while Burns etal.³⁵ inserted nanopores into vesicles, which then adhered to a glass nanopipette.⁴³ Usually, the bilayer system exerts minimal influence on the conductance of protein pores with some exceptions,⁴⁴ but DNA nanostructures could be more flexible⁴² or compressible than protein pores, leading to altered conductance.

With the aim to address, settle, and clarify the above questions, we characterize a DNA nanopore of the archetypal six-helix-bundle architecture (Figure 1A) via single-channel current recordings. To establish the (i) experimental width of the DNA channel, we used sizing with poly(ethylene glycol) (PEG). In this approach, the ionic conductance is measured in the presence of PEG of varying length to determine the threshold size under which the organic polymer permeates into the pore to block or affect the ionic current.^45,46 By probing the diameter of the DNA pore with PEG, it should (ii) be possible to establish that the main ion-conducting path runs through the membrane-spanning channel. Furthermore, we address (iii) the inconsistent conductance values by examining pore current as a function of transmembrane voltage, and (iv) by using planar lipid bilayers as well as vesicle recordings (Figure 1B and C) on a single pore, something that has not been done before. By exploring several tunable parameters we aim to identify conditions that can account for the different conductance values. In brief, our report settles and answers all four points and demonstrates that DNA nanopores are well-defined structures within the selected parameter space.

Figure 1.

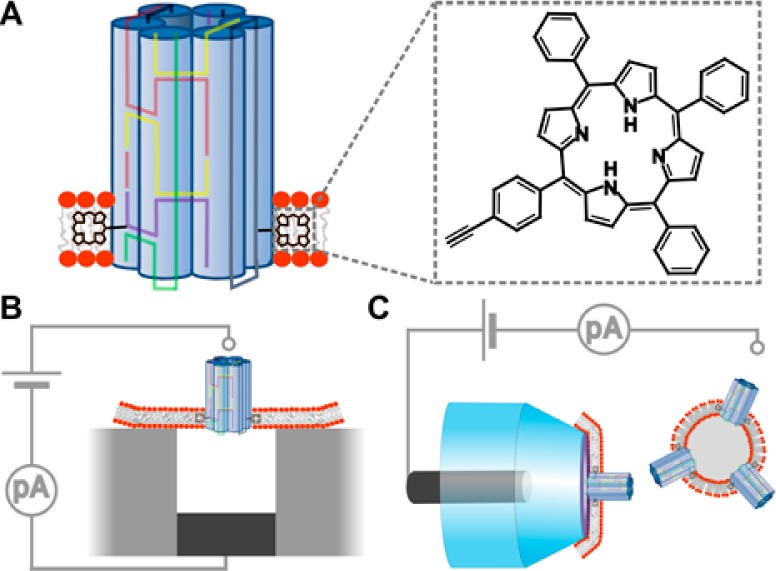
DNA-based membrane-spanning pore and the two recording setups used to measure the conductance properties of the nanopore. (A) Schematic drawing of a six-duplex-bundle nanopore composed of six DNA oligonucleotides (colored) carrying two tetraphenyl porphyrin tags (black, inset), which anchor the pore into the lipid bilayer. The porphyrin anchor is attached via the acetylene group (inset) to position 5 of a uridine base (not shown). (B) Schematic drawing of a microcavity unit with a suspended planar lipid bilayer. Only one of the 16 units of the recording chip is shown. The nanopores were incorporated into the preformed lipid bilayers. (C) In the second recording setup, the nanopores were initially incorporated into lipid vesicles, which were then spread over the orifice of a 200 nm diameter glass nanopipette (transparent blue). The grounded reference electrodes in B and C are drawn as small, light gray circles, while the other electrode is in dark gray.

Results

Design and Formation of DNA Nanopores

To facilitate the comparison to previous studies,³³⁻³⁵ we built a DNA nanopore with the archetypal six-helix-bundle architecture. In this design, six DNA duplexes are arranged in a hexagon to enclose an approximately 2 nm-wide channel (Figure 1A). In the channel described by Burns etal.³⁵ and replicated in this report, the nanobarrel is composed of six DNA oligonucleotides, which thread between the duplexes to form crossovers and add structural stability. The resulting six-helix bundle has a nominal width of 6 nm and a height of 14 nm. Two tetraphenyl porphyrin tags are coupled to one terminus of the nanobarrel to facilitate its insertion into the bilayer (Figure 1A, inset). The synthesis of the tetraphenyl porphyrin, its coupling to form a modified uridine nucleoside, and its incorporation into DNA strands via solid-phase oligonucleotide synthesis have been described.^47,48

The DNA nanopore was assembled by heating and cooling an equimolar mixture of four native and two porphyrin-modified DNA strands (for sequences see Supporting Information, Table S1, Figure S1). The assembly mixture was analyzed by native agarose gel electrophoresis to confirm the formation of the DNA nanopore. The band migrated to the same height as a control nanopore without the porphyrin tags (Figure 2A, lanes 1 and 2, respectively), suggesting assembly of the correct DNA pore and the absence of misfolded products.

Figure 2.

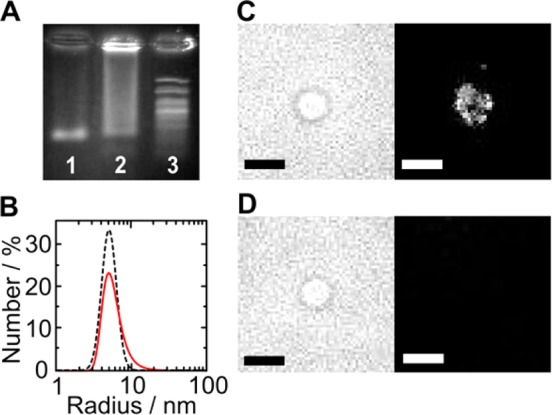
DNA nanopores are self-assembled and embedded into lipid bilayers. (A) Native agarose gel electrophoresis of DNA nanopores without (lane 1) and with the porphyrin lipid anchor (lane 2) 100 bp molecular weight marker (lane 3). (B) Dynamic light scattering trace of a DNA pore with lipid anchor (red line) and without lipid anchor (black dashed line). (C, D) Bright-field (left) and confocal fluorescence images (right) of DPhPC vesicles incubated (C) with DNA pores carrying the fluorescent porphyrin tag and (D) with Cy3-labeled nanopores lacking a lipid anchor. The bright spots in (C) may represent individual or clusters of pores. Excitation wavelength: 532 nm. Scale bar: 5 μm.

Band streaking has been observed before and is caused by interactions of the hydrophobic tag rather than unfolding.^33,47,48 Dynamic light scattering of the nanopore with the lipid anchors revealed a single major peak at a hydrodynamic radius of 5.5 ± 0.2 nm (Figure 2B, red line), which is in agreement with the calculated value of 4.9 nm.^49,50 The radius for the control pore without an anchor was slightly smaller, at 5.2 ± 0.2 nm (Figure 2B, black dashed line). Fluorescence microscopy established that the pore with the fluorescent porphyrin tag^51,52 attached to the lipid bilayer of giant unilamellar vesicles (Figure 2C). By contrast, the signal of nanopores carrying a Cy3 tag but no lipid anchor did not localize into the curved membrane (Figure 2D), in line with expectations.

Single-Channel Current Analysis and PEG Sizing Confirm that the DNA Nanopores Adopt, at Low Voltages, the Open-Channel Structure Corresponding to a High-Conductance State

With the aim to settle fundamental questions (i) and (ii) about the DNA channel’s diameter and the main ion-conducting path, respectively, we subjected the porphyrin DNA nanopores to single-channel current recordings. Planar bilayer recordings (Figure 1B) were conducted with the recently developed multicavity parallel analysis platform, Orbit 16, from Nanion⁵³ using standard electrolyte conditions (1 M KCl, 10 mM HEPES, pH 8.0). Ionic flow through the pore was triggered by applying a transmembrane potential. At +20 mV relative to the grounded cis side (Figure 1B), the trace of the DNA nanopore shown in Figure 3A had a stable current of 33 pA, corresponding to a conductance of 1.65 nS. Averaging the conductance values from over 50 single-channel current traces at +20 mV yielded a value of 1.62 ± 0.07 nS and a narrow distribution in the conductance histogram (Figure 3B). The experimental value is higher than the theoretical prediction of 1.32 nS calculated⁵⁴ using the nominal pore geometry. But this calculation assumes a pore with electrically nonpermeable walls, which is most likely not correct for DNA pores. A comparison also has to consider that the diameter of hydrated DNA duplexes may be bigger than 2 nm. Pores with a conductance of around 1.6 nS are referred to as being in the high-conductance state.

Figure 3.

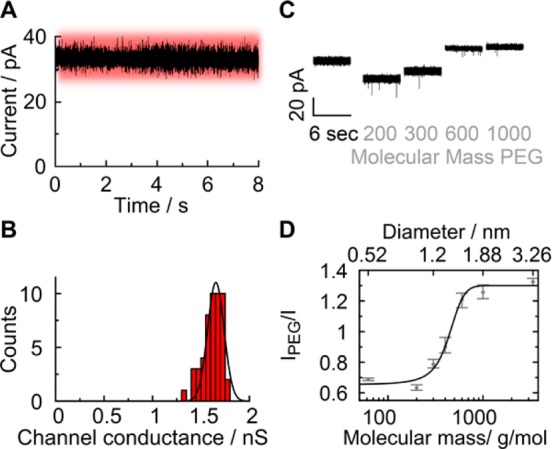
High-conductance state of membrane-embedded DNA nanopores at low voltages corresponds to an open pore as shown by PEG sizing. The traces were obtained with planar lipid bilayer recordings. The high conductance state is color-coded in red. (A) Representative ionic current trace at +20 mV. (B) Histogram of channel conductances obtained from measurements at +20 mV. (C) Current traces of individual pores in the absence and presence of PEG molecules of indicated mean molecular mass. (D) Pore blockade as a function of the hydrodynamic diameter of PEG. Between PEG 200 and PEG 600, there is a significant change in relative pore blockade. With PEG 1000 and above the effect is tapering off. This upper turning point indicates that PEG molecules are being excluded from the pore lumen. The hydrodynamic diameter of PEG 1000 (approximately 1.9 nm) is hence assumed to reflect the diameter of the DNA pore. The data present averages and the minima and maxima from five independent recordings (PEG 62 to PEG 400) and three independent recordings (PEG 600 to PEG 3350).

To address question (i) on channel diameter, the pores in the high-conductance state were subjected to PEG sizing to probe the channel’s diameter. The nominal inner width is 2 nm, but this has not been verified by experimental means. The sizing approach has been used previously to determine the inner width of protein channels.^45,46 It relies on measuring the pore conductance in the presence of PEG molecules of different hydrodynamic diameters. Molecules smaller than the channel width are expected to permeate into the lumen and reduce or change the pore conductance. By contrast, larger PEG probes unable to move into the pore should have no blocking effect on conductance. For the sizing experiments, PEGs with a mean molecular mass of 62, 200, 300, 400, 600, 1000, and 3350 Da covering a range of hydrodynamic diameters from 0.52 to 3.26 nm were used (see the Methods section for information on the mass dispersity).^45,46 PEG was added to the cis side of the DNA nanopore to a final concentration of 0.2 g/mL, and the conductance was measured after equilibrating for approximately 10 min. The polymeric probe led to a size-dependent reduction in the pore current, with PEG 200 (Figure 3C) and PEG 62 (Figure S2) marking the biggest drop. The current reduction implies that the polymers enter the pore and reduce ionic flow via steric effects. The blockade levels for PEG 62 and 200 are similar, as they represent the PEG effect on the bulk solution; that is, there is no size discrimination by the pore. By comparison, starting with PEG 300 (Figure 3C) the channel conductance increased (PEG 400, Figure S2) drastically at PEG 600 up to PEG 1000, where it leveled off (Figure 2C) with no major change at PEG 3350 (Figure S2). The saturation indicates that the largest PEG molecules were too big to enter the channel lumen. We note that the current levels for PEG 600 up to PEG 3350 were higher than the pore current in the absence of PEG. This reflects the higher effective concentration of electrolyte ions, or activity, within these PEG solutions, as observed previously.^55,56

Plotting the relative current change versus the hydrodynamic diameter of PEG revealed a sigmoidal dependence and an upper transition point with a cutoff at 1.9 nm hydrodynamic diameter (Figure 3D). The diameter reflects the size of PEG which does not enter the pore due to steric exclusion and is in excellent agreement with the expected nominal diameter of the DNA nanopore of 2.0 nm.³⁵ We are aware that the sizing of pores with PEG relies on the simplifying assumption that the behavior of PEG in the pore is similar to that of bulk PEG. While this is correct in several cases, deviations are known,⁵⁷ as also discussed in two reports which size PEG with a protein of known structure.^58,59 For example, PEG can bind cations,^60,61 and the threshold size of PEG for permeation into a protein pore was found to depend on the pH-dependent ionization of amino acids inside the channel lumen.⁶² Hence, we cannot rule out that our transition point of 1.9 nm might be biased by electrostatic interaction between PEG and the negatively charged DNA pore wall. The size-dependent change of the plot in Figure 3D argues, however, against any possible strong bias.

The constant-current trace for blocked pores suggests that multiple PEG molecules simultaneously reside inside the pore as opposed to individual polymers passing or lodging inside the lumen one at a time. Multiple PEG molecules do not lead to a 100% pore current reduction because the polymer’s loose structure carries electrolytes. Furthermore, ion permeable⁴¹ channel walls may bypass and effectively dilute out the blocking effect of PEG. The major outcome of the PEG sizing is the confirmation of the pore’s diameter once inserted within bilayers.

Sizing the channel width with PEG also settles question (ii) by demonstrating that the main conductance path—at least for the membrane-spanning section of the pore—is inside the channel. The threshold diameter of approximately 1.9 nm is not compatible with a competing model in which ions pass solely through a suggested gap between lipid bilayer and pore; a membrane hole this size would not be energetically stable for our minute-long measurement times used in our PEG sizing experiments. However, it cannot be ruled out that a small proportion of the current runs outside the DNA channel through temporarily occurring gaps between the outer pore wall and the lipid bilayer.

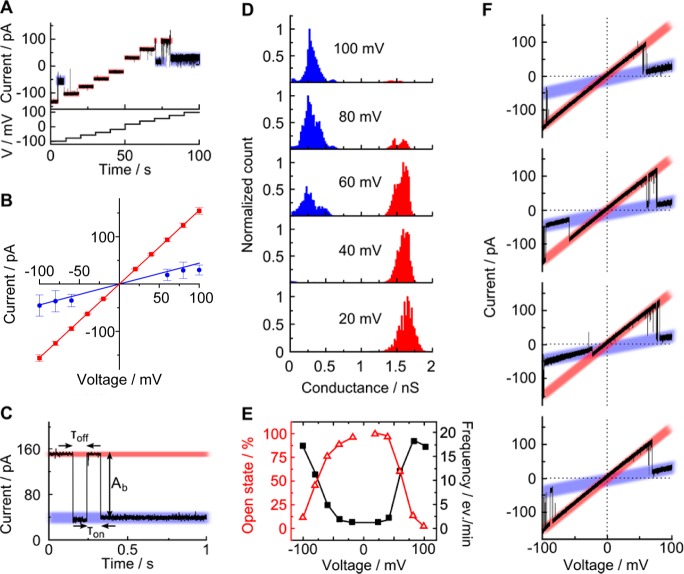
Higher Voltages Lead to a Lower Conductance State Representing a Partially Blocked Channel

In order to clarify point (iii) about the different conductance values reported in the literature, we examined the pore current as a function of transmembrane voltage, which is a key parameter for many membrane channels. As illustrated for a single-channel current trace, increasing the potential’s magnitude in 20 mV steps initially confirmed the presence of the established high-conductance state for the range from −60 to +40 mV (Figure 4A, red section). But applying voltages of <−80 mV or >+60 mV revealed a lower conductance state (Figure 4A, blue section). The voltage-dependent two-state behavior was confirmed in prolonged single-channel current traces for all voltages (Figure S3). When summarized in a current-voltage plot, the high-conductance state was ohmic (Figure 4B, red symbols), in line with the expected cylindrical shape of the DNA channel. By comparison, the low-conductance state was ohmic for a given pore, and slightly varying low-conductance levels were found for different pores (Figure 4B, blue symbols). Pores stayed temporarily or for a longer time in the low-conductance state, as illustrated for several single-channel current traces (Figure 4C, Figure S3). The durations of these blockades, τ_off (Figure 4C), were found to spread from 10 ms to several seconds (Figure S4). Possible molecular mechanisms causing the lower conductance state include electric-field-induced fraying of DNA duplexes, flipping of DNA loops at the pore entrances, conformational alterations in the overall duplex structure or the relative position between duplexes, or repositioning of the pore within the bilayer.

Figure 4.

Low-conductance state for DNA nanopores occurs at higher voltages. The high conductance state is color-coded in red; the low conductance state is coded in blue. The traces were obtained with planar lipid bilayer recordings. (A) Current traces for 20 mV voltage steps showing that potentials of <−80 mV and >+60 mV lead to a low-conductance state. (B) IV curve displaying the averages and standard deviation from 7 single-channel current traces. (C) Representative single-channel current trace at +100 mV. The amplitude of the blockade, A_b, the event dwell time, τ_off, and the inter-event interval, τ_on, are defined. (D) Cumulative all-point histogram of 38 single-channel current traces for +20 to +100 mV in 20 mV steps illustrating the voltage-dependent switching between the low-voltage open state and the high-voltage partially closed state. (E) Probability of observing the open state as a function of voltage. The probability (red line) is defined as the count for the high-conductance state divided by all counts in the all-point histogram. The black line represents the frequency of occurrence for the low-amplitude events as reported in Table S2. Error bars for the open probability are not given as the conventional way of obtaining averages from Poisson-fits for τ_on value distributions is not possible when the probabilities are obtained by Gaussian fitting of peaks in all-point histograms. For the frequency of occurrence, there were not enough closing events at small voltages to derive meaningful errors. (F) Traces of a single DNA pore recorded at multiple consecutive voltage ramps running from −100 to +100 mV. The occurrence of the low-conductance state at −20 mV in the third trace rather than at usual voltages of around −80 mV is explained by a memory effect of this particular DNA structure, which had experienced previous voltage ramps and pore closures.

To obtain statistically relevant values for the low- and high-conductance states and their voltage-dependent occurrence, we characterized multiple channels via all-point histogram analysis. Data from 38 independent single-channel traces recorded in 20 mV steps from +20 mV up to +100 mV were combined in a series of cumulative all-point histograms (Figure 4D; Figure S5 for −20 to −100 mV). The two-state behavior is clearly demonstrated in the plot by the big peaks for low- and high-conductance states at 0.25–0.5 and 1.6 nS, respectively. Slight variations of conductance within those two dominating states likely represent subconductance levels, which are, however, not discussed further to maintain our focus on the major changes in conductance and pore behavior. The conductance difference between the two levels was also established by independently calculating the blockade magnitude A_b (Figure 4C, Figure S4). The histogram analysis in Figure 4D furthermore confirmed that the low-conductance level first appeared at +60 and −80 mV and dominated at higher voltages (Figure S5), in agreement with a related voltage-dependence for the characteristic inter-event interval τ_on (Figure S6). To quantify the effect of voltage on pore conductance, we derived the counts for the high-conductance state from the all-point histograms and plotted these probabilities against voltage (Figure 4E, red line). The high-conductance state had a probability of 97% at the lowest recorded voltage of +20 mV. The threshold voltages for 50% probabilities were +64 and −77 mV, which are close to the threshold voltages attained when plotting the frequency of occurrence of blockade events (Figure 4E, black line; Table S2).

Our data on the voltage-switching of a DNA nanopore between a high- and a low-conductance state address in part point (iii) on the discrepancy between published conductance values. The high conductance for the 14 nm pore at 1.6 nS is now higher than the conductance of 0.89 nS of the 42 nm pore by Langecker etal.,³³ in line with expectations that a pore with a shorter conductance path yields a higher conductance than a pore with a longer channel. In further agreement, the low-conductance state at 0.25–0.4 nS from Burns etal.³⁵ was well reproduced with a value of 0.36 ± 0.1 nS obtained by our conductance histogram (Figure S7). In our present study, these two states are reversibly interconvertible (Figure 4D) as additionally confirmed by consecutive voltage ramp traces of a single pore (Figure 4F). But the previous report by Burns etal.³⁵ and another study with a related six-duplex-bundle pore³⁴ did not describe the interconversion and current values corresponding to the high-conductance state. Hence, question (iii) is not completely resolved. One possible explanation is that the conductance values may be attributed to the two different recording setups, as the data in Figures 3 and 4 were acquired with planar lipid bilayer recordings, while the previous report by Burns etal. used lipid bilayers mounted on a glass nanopipette.³⁵ This previous study focused on the chemical and structural characterization of the nanopores, and an in-depth conductance analysis with nanopipette membranes could reveal the low-conductance state. However, the related six-duplex-bundle pore was characterized by planar bilayer recordings, but other factors might have favored the preferential recording of the low-conductance state.³⁴ These include the analysis at a high voltage of 100 mV and the use of the different lipid anchor system composed of 72 ethyl phosphorohioate groups.³⁴ This may not be comparable to the structurally less intrusive anchoring strategy of the present pore with solely two hydrophobic porphyrin tags.

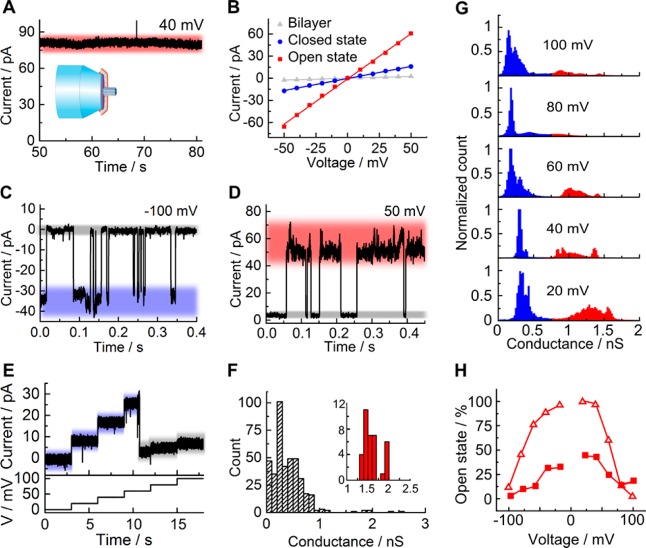
Nanopores Embedded into Nanopipette-Mounted Membranes Have a Greater Tendency to Show a Lower Conductance State

We examined the porphyrin-based DNA nanopores with a second recording technique to address point (iv) about the lack of comparability between previous studies that examined different pores with different recording techniques. For the current measurements, lipid vesicles with embedded nanopores were mounted onto glass nanopipettes typically under small negative pressure (−1 to −10 PSI) to spread the membrane over the orifice (Figure 1C).⁴³ Similar to the planar membranes, nanopore recordings with the nanopipette membranes gave rise to the known stable high-conductance state of around 1.5 nS for moderate voltages, as shown for a single-channel current trace at +40 mV (Figure 5A) and an IV curve (Figure 5B). We note that these traces were less frequent than on the planar setup. Furthermore, nanopipette-bilayer traces displayed current fluctuations (Figure 5C and D), which were, however, normally not between the high- and the low-conductance state as found for planar bilayers, but predominantly between either of these levels and a completely closed pore (Figure 5C and D). Indeed, pores in the nanopipette system also permanently closed (Figure 5E). A conductance histogram combining all nonzero current levels recorded at +100 mV (Figure 5F) displayed the major low-conductance state with a value of 0.24 nS, which is close to Burns etal. and the less frequent high-conductance state (Figure 5F, inset).

Figure 5.

Conductance analysis of DNA nanopores embedded in lipid bilayers mounted across a nanopipette orifice. (A) Single-channel current trace of a pore in the high-conductance state at +40 mV. (B) IV curves for single DNA nanopores in the high and the low-conductance state and a lipid bilayer without pores as reference. The data spread for the two pore conductances can be estimated from the peak width in the all-point histograms in panel D. (C, D) Single-channel current trace fluctuating from the (C) low- and (D) high-conductance state to a completely closed pore. (E) Voltage-stepped current trace of a low-conductance state switching to complete and permanent pore closure at +80 mV. (F) Conductance histogram derived from single-channel current recordings at +100 mV. (G) Cumulative all-point histogram of 21 current traces from +20 to +100 mV in 20 mV steps. (H) Probability of observing the open state as a function of voltage. The probabilities were derived from all-point histograms as described in Figure 4. Filled squares show data from the nanopipette-mounted membrane, while empty triangles are data from planar bilayer recordings.

To determine the influence of voltage, a series of cumulative all-point histograms were plotted to combine the conductance data recorded from +20 to +100 mV at 20 mV steps (Figure 5G). Similar to planar bilayer recordings, the two peaks for the high- and the low-conductance level were clearly visible, and higher voltages shifted the distribution from the former to the latter conductance state (Figure 5G; for a side-by-side comparison of planar and nanopipette bilayer data see Figure S8).

As a difference, the distribution of the high conductance level in the nanopipette system was broader, and lower voltage magnitudes were able to shift the conductance distribution to the low-level state (Figure 5G, Figure S8). To quantify and compare the effect of the membrane system on pore conductance, we plotted the voltage-dependent probabilities for the high-conductance state, which represent the corresponding counts in the all-point histograms. For the nanopipette bilayers, the probabilities were 35% and 45% at −20 and +20 mV, respectively (Figure 5H, filled squares). This compares to 88% and 97% for the planar bilayers (Figure 5G, empty triangles; data replotted from Figure 4 to facilitate comparison).

Conclusions

Our results establish that the DNA pore resides, at low voltages, in a high-conductance state, which is in excellent agreement with an open channel of diameter close to expectations. Directly experimentally validating the diameter of the bilayer-embedded nanopores by probing the lumen with polymers of known size has not been achieved before. Similarly, our report is the first to clarify that the membrane-spanning section of the channel is indeed the main ion-conducting path. Our finding of the voltage-dependent switching between the open and partially closed state is important. It helps reconcile previously reported, conflicting conductance values by showing that the newly discovered open state of the 14 nm long pore has, in line with predictions, a higher conductance than a longer pore with the same six-helix-bundle design. We also pioneer the conductance characterization of DNA nanopores with planar bilayer recordings as well as bilayers mounted on the tip of a nanopipette, thereby establishing a reference standard. The two analysis methods gave consistent and partly overlapping yet different results. Both systems reveal the open and partially closed states and the voltage-induced switching between them. However, the planar bilayer system leads to a higher probability of the open channel at lower voltages and a narrower conductance distribution in the open channel state. Possible reasons for the difference could include, in the case of the nanopipette, the presence of lateral membrane pressure, which might compresses the pore to change the ion-conducting path, or, in the case of the planar bilayers, the use of detergents to facilitate pore insertion. The exact reason for the differences will be examined in future studies, which will also decipher the molecular nature of the partial blockage of the DNA pore at high voltages.

Methods

Design and Synthesis of Nanopore Structure

The nanobarrel was designed following the honeycomb lattice of caDNAno software⁶³ including the modification³⁵ of linking termini of staple and scaffold strands to obtain an architecture with six DNA strands. The positions for attaching porphyrins were selected on two opposite duplexes using a molecular model generated with Macromodel. The tetraphenyl porphyrin-tagged deoxyuridine was synthesized and incorporated into DNA oligonucleotides,^47,64 the purity of the synthesized DNA strands was confirmed by PAGE, and the yield was determined by UV–vis spectroscopy.³⁵ Nanopores were assembled by heating at 95 °C for 5 min an equimolar mixture of the six strands at 1 μM each dissolved in buffer A (1 M KCl, 50 mM Tris, pH 8.0; total volume 1000 μL) followed by cooling to 16 °C at a rate of 0.25 °C per min in a Varian Cary 300 Bio UV–vis spectrophotometer equipped with a Peltier cooling element.

Nanopore Characterization with Native Gel Electrophoresis, Dynamic Light Scattering, and Fluorescence Microscopy

The DNA nanopores were analyzed using 1.2% agarose gel electrophoresis in standard TBE buffer supplemented with 11 mM MgCl₂.³⁵ Dynamic light scattering measurements were carried out on a Zetasizer Nano S from Malvern⁶⁵ using DNA samples with a concentration of 0.25 μM in buffer A. For fluorescence microscopic imaging of nanopores embedded into lipid bilayers, giant unilamellar vesicles (GUVs) in the range 1–30 μm were prepared using an electroformation unit (Vesicle Prep Pro, Nanion Technologies, Germany) as described.^66,67 The GUVs (0.5 μL) suspended in 1 M KCl and 50 mM Tris, pH 8.0, were incubated with DNA nanopores at a final concentration of 3 nM for 10 min at RT. The suspension (20 μL) was then imaged using a previously described microscopic setup⁶⁸ with a 532 nm laser operating at 2 mW and an EMCCD camera (acquisition time of 5 ms). Data acquisition and image processing were performed as described.⁶⁸

Nanopore Current Recordings

For planar lipid bilayer electrophysiological current measurements, an integrated chip-based, parallel bilayer recording setup (Orbit 16, Nanion Technologies, Munich, Germany) with multielectrode-cavity-array (MECA) chips (IONERA, Freiburg, Germany) was used. Bilayers were automatically formed by remotely actuated spreading 1,2-diphytanoyl-sn-glycero-3-phosphocholine (DPhPC, Avanti Polar Lipids, Alabaster, AL, USA) dissolved in octane (10 mg mL^–1). The standard electrolyte solution was 1 M KCl and 10 mM HEPES, pH 8, unless stated otherwise. For pore insertion, a 2:1 mixture of porphyin-anchored DNA nanopores and 0.5% OPOE (n-octyloligooxyethylene, in 150 mM KCl, 10 mM HEPES, pH 8) was added to the cis side of the bilayer to a final concentration of 10 nM nanopores. A positive voltage of +40 mV was applied to facilitate pore insertion. Successful incorporation was observed by detecting the current steps to distinct levels. To estimate the size of the pore diameter, currents were recorded in 1 M KCl and 10 mM HEPES, pH 7.5, containing 0.2 g mL^–1 poly(ethylene glycol) with an exact molecular mass of 62 and mean molecular masses of 200 (M_n ranging from 190 to 210), 300 (M_n 285–315), 400 (M_n 380–420), 600 (M_n 570–630), 1000 (M_n 950–1050), and 3350 (M_n 3015–3685) (Sigma-Aldrich, Munich, Germany). For equilibration, the solution in the cis chamber was mixed by careful and repeated pipet aspiration. Equilibration was achieved when there was no change in measured current. To measure the conductance of a given single channel with respect to PEG with molar masses of up to 400, polymer in the electrolyte solution in the cis chamber was removed by repeated washing to obtain the original nonblocked current, followed by adding the next PEG polymer and mixing. For PEG 600 and higher, the conductance of pores was measured only for a given polymer size, as washing out of the probe molecules would have taken more than an hour. The data points for PEG 600 to PEG 3350 were obtained using a DNA pore of the same hexagonal six-duplex-bundle scaffold but carrying cholesterol anchors at the outer pore wall. The cholesterol pores had the same conductance values from PEG 62 to PEG 400 as the DNA pores with the porphyrin anchors. The data were Bessel filtered at 2.873 kHz and acquired at 10 kHz with an EPC-10 patch-clamp amplifier (HEKA Elektronik, Lambrecht/Pfalz, Germany) with the PATCHMASTER software (HEKA Elektronik). Single-channel analysis was performed using Clampfit (Molecular Devices, Sunnyvale, CA, USA).

The recordings for nanopores inside lipid vesicles were performed using a nanobilayer setup as previously described.⁴³ Bilayers were formed reproducibly by bursting GUVs on the tip of a nanopipette (200 nm diameter). GUVs were incubated with 30 nM DNA nanopores for 10 min at RT in buffer A. Bilayers that held DNA nanopores were identified due to their lowered seal resistances. Nanopore incorporation was often triggered by applying a voltage pulse. Ionic current data were acquired using an Axopatch 200B amplifier and analyzed as described.^43,69

Author Contributions

^⊥ A. Seifert and K. Göpfrich contributed equally to this work.

Supporting Information Available

Experimental details on DNA sequences for assembling the DNA nanopores. Experimental results on the conductance properties of DNA nanopores. This material is available free of charge via the Internet at http://pubs.acs.org.

The authors declare no competing financial interest.