Abstract
For the applications of hard X-ray Propagation-based Phase-contrast Computed micro-Tomography (PPCT) in high-resolution biological research, both the high spatial resolution and high contrast-to-noise ratio are simultaneously required for tiny structural discrimination and characterization. Most existing micro-CT techniques to improve image quality are limited by high cost, physical limitations, and complexity of the experimental hardware and setup. In this work a novel PPCT technique, which combines a wavelet transform based modulation transform function compensation (MTFC) algorithm and a generalized phase retrieval algorithm, is proposed to optimize the reconstruction quality of tomographic slices. Our experimental results, which compared the spatial resolutions and contrast-to-noise ratios of reconstructed images, demonstrated the validity of the proposed generalized PPCT technique. The experimental results showed that the proposed generalized PPCT technique is superior to the direct PPCT technique and the linearized phase retrieval PPCT technique. This novel PPCT technique demonstrates great potential for biological imaging, especially for applications that require high spatial resolution and limit radiation exposure.
1. Introduction
X-ray micro-tomography has been widely utilized in nondestructive three-dimensional imaging of internal structures of objects in medicine, biology, and materials science [1,2]. Conventional X-ray micro-tomography is based on the differential X-ray attenuation by constituents of an object. This contrast mechanism is effective for distinguishing between elemental components with significant differences in atomic number or electron density. However, the technique can't provide significant attenuation contrast for low absorption objects such as soft tissues or low-Z materials. On the other hand, X-ray phase sensitive micro-tomography can be utilized to improve the contrast in transmission images of the weak-absorbing samples, because the phase factor is about 1000 times greater than the absorption factor for light elements in hard X-ray region [3–5]. Among all phase imaging techniques, the PPCT, shown schematically in Fig. (1), is the simplest to implement without the need of additional complex optical components [6,7]. For the direct PPCT technique, the phase-shifted X-ray diffracts and generates dark-bright interference fringes at boundaries and interfaces of samples, which also identify the effects of edge enhancement or refraction enhancement, particularly essential for the discrimination of micro-structure information. However the direct PPCT provides only the apparent linear attenuation coefficient (LAC) of an object, rather than the true LACs. This technique may present anomalously large or even negative apparent LAC values at interfaces and boundaries. These "artifacts" may cause faulty interpretation of sample structures, and impede even qualitative characterizations for tissues and materials [8,9]. In addition, the bulk-area contrasts, away from the regions of boundaries and interfaces, are rather weak due to the tiny differences in apparent LACs between bulk components. Therefore, the Phase Retrieval (PR) is required for overcoming the two defections of the direct PPCT. The PR-based PPCT technique usually can be performed as a two-stage process: first the projected phase map is retrieved from the raw projections, and then three-dimensional tomographic images are reconstructed with the standard Filtered Back-Projection (FBP) algorithm. There have been several single-distance phase retrieval algorithms, following the same mathematical pattern despite their different origins and approximations adopted [10–15]. They measure the intensity to calculate the phase distribution at the contact plane by multiplying its Fourier transform with a transfer function (a low-pass filter in frequency domain). In this way one achieves more pronounced phase contrast for weakly absorbing samples, reduces artifacts and enables quantitative tomography [16]. Meanwhile, inappropriate phase retrieval can partially causes a blurring phenomenon and lower spatial resolution, such as broadened blurring boundaries and interfaces in the sample's structural details.
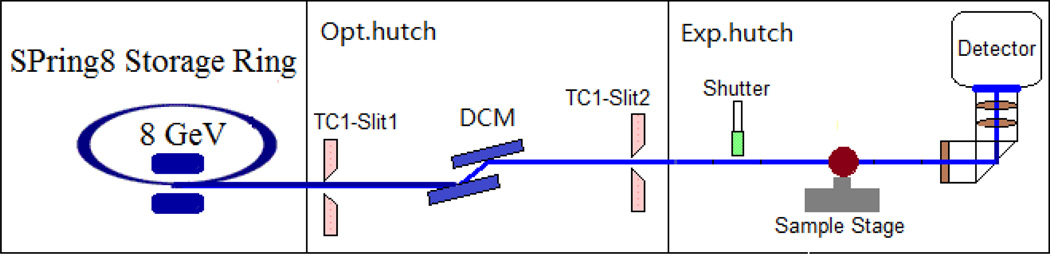
Fig. 1.
Schematic of experimental setup at the BL20B2 beamline.
Our central proposition for image quality improvement is to simultaneously optimize both the spatial resolution (sharpness) and the contrast-to-noise ratio of tomographic reconstruction images. We investigated the direct PPCT and PR-based PPCT technique with considering the overall factors causing the blurring phenomenon in two aspects: direct problem and inverse problem. The direct problem is about the degradation of imaging formation, such as the point spread function of optical system, caused by source density distribution, finite pixel size et al. The blurring in the inverse problem results from the inappropriate phase retrieval, which unduly suppresses high frequency counterparts in the high-resolution X-ray micro-tomography. In order to optimize the high-resolution image quality, combining good sharpness and high contrast-to-noise ratio, we utilize the MTFC with wavelet transformation to process the imaging formation to solve direct problem, then modify the linearized PR algorithm (LPR) to improve the inverse filtering in phase retrieval. The main procedures are summarized in the following sections: First, the measured MTF of the imaging system was implemented to the method of MTFC. Second, the single projection dataset were processed with using a generalized phase retrieval algorithm, as is described below in Section 2.3. Third, from the angular phase-retrieved projections, three-dimensional tomograms are reconstructed by using the standard FBP algorithm. Finally we compared the direct PPCT technique to several PR-based PPCT techniques, which include a linear PR algorithm and a generalized PR algorithm incorporating the MTFC de-blurring. The comparisons are conducted based the spatial resolution (sharpness) and contrast-to-noise ratio (CNR) of the reconstructed images.
2. Materials and Methods
2.1 Image acquisition
The experiment was carried out at experimental hutch 1 (45m from the light source) of the medical and imaging beamline (BL20B2) in SPring8 (Hyogo, Japan). The radiation from the bending magnet on a 8.0GeV storage ring is monochromatized with a SPring8 standard Double Crystal Monochromator (DCM) using Si (111) reflection. The flux density at the sample is 6.5×109 photons·mm−2·s−1 for 15keV X-rays. The experimental setup is depicted in Fig. 1. Fast shutter, sample stages and X-ray image detector were placed in the experimental hutch. The fast shutter and the high precision stages were made by Kohzu Precision. The shutter is driven by TTL signal. It takes 5 ms to open 4 mm aperture in vertical direction. The stages have a resolution of a few micrometers. The pulse motor controller (PM16C-02N, Tsujidenshi, Japan), the prescaler (homemade at SPring8) and the delay pulse generator (BNC 505, Berkeley Nucleonics Corp, USA) synchronized via TTL signal during the micro-tomographic scan. It means that the fast shutter and the X-ray image detector also follow the TTL signal, and the measurement timing of all of components is fixed by pulse motor controller. The X-ray image detector consists of a beam monitor with a 10-um-thick P43 (Gd2O2S:Tb+) phosphor screen equipped with a f=35mm camera lens (Ai AF Nikkor 35mm F1.4D, Nikon, Japan) and a CMOS camera (C11440-22C, Hamamatsu Photonics) coupled with a f=85mm camera lens (Ai AF Nikkor 85mm F1.8D, Nikon, Japan), which magnify the image by about 2.43 times on the CMOS chip for yielding effective pixel size of 2.7µm.
The measurements were investigated at 15keV with the sample-to-detector distance (SDD) 150mm. 900 raw images were acquired at every projection angle with 25ms of exposure time. Two different samples were employed as following: (i) the cylinder of standard PMMA (C5H8O2) with a diameter Φ=1mm, 1.19 g/cm3, made by Good Fellow Cambridge Limited, Huntingdon, UK, was tested to measure the accuracy of our presented method with phase distribution and (ii) a kind Chinese herb named cordyceps sinensis, containing rich microstructures of porous cluster, was used for verifying the validation of the modified PPCT technique for high resolution biological research.
2.2. Direct Problem: Imaging Formation
2.2.1 Degradation Model in Propagation-based Imaging
Considering the case of illumination an object with partially coherent X-rays of wavelength λ, and moving the detector a relatively short distance D downstream from the object, the intensity formed is called a Fresnel diffraction pattern. In terms of the exit wave, free space propagation can be considered a linear space invariant (LSI) system, e.g. the synchrotron-based PPCT. The recorded intensity is the squared modulus of the exit wave: ID(x,y) = |T(x,y)*PD(x,y)|2 where * denotes convolution, T (x, y) is an object transmitted function and PD (x, y) is the Fresnel propagator in the spatial coordinates [17]. The direct problem is then efficiently addressed by calculating the convolution in Fourier domain and the two-dimensional Fourier transforms can be rewritten as . For all practical LSI imaging system, e.g. source intensity distribution, finite pixel size et al, the degradation model of imaging formation is given as in the Fourier domain [18]:
| (1) |
Where k and the symbol * denote the normalization factor and the convolution operator respectively. The model represent the relationship among observed image , original image , the additive noise Na(u,v) and multiplicative noise Nm(u,v) mainly arising from the average of dark currents and the average of background respectively. On the basis of the degradation model, the lost information is recovered via the denoising and deblurring processes. Actually, the relevant noises can be greatly suppressed by the normalization background correction of every angular projections of PPCT, tremendously improving the signal-to-noise ratio (SNR). Using a logarithm, the multiplicative noise is converted to additive noise, which is erased with utilizing wavelet threshold denoise. The basic deblurring principle is to measure the descend degree of the MTF of the system, then calculate the ascend degree of the high frequency part of the target image. The restored image using MTF compensation in Fourier domain is given below:
| (2) |
2.2.2 MTF Compensation based on Wavelet Transform
The MTF Compensation is employed based on wavelet transform, which represents an image as sum of wavelet functions with different locations and scales [19]. Using a pair of analysis filters (low-pass filter L and high-pass filter H), the original image is exactly reconstructed from the coefficients of the basis. Let us assume that the qth level image has a size of ξ⃗, where q=1,2,3… is the level of the decomposition and η⃗ is the size of origin image [20]. The procedures of image wavelet decomposition based on FFT include the following:
- Considering a vector sequence
where a(n) and b(n) are real coefficient with same length, corresponding to L and H filters for n=1,2,3…K/2q. In Eq.(3), ξ⃗ and η⃗ denote the horizontal and vertical unit vectors, respectively. Note that L and H are orthogonal mirror filters and a vector. The Fourier transform (FT) of Eq.(3), x(N), and its transposed form, xT(N), are expressed as:(3) (4)
Let T0(u,v) = ID(u,v), where T0(u,v) denotes the FT of the finest scaling coefficients for u,v=1,2…, Yq (u,v) = Cq−1 (u,v)· W(u,v).(5) - Two dimensional filter coefficients W(u,v) are denoted as
where ⊗ represents matrix multiplication.(6) - The qth level decomposition for the image is written as
Taking inverse FT of Eq.(7), we obtain(7)
where fLH(m, n), fHL(m, n), fHH(m, n), and fLL(m, n) are the coefficients of horizontal, vertical, diagonal details, and approximation, respectively.(8) - Downsampling from yLH(m, n), yHL(m, n), and yHH(m, n), we get the horizontal, vertical, and diagonal detail subiamges, respectively. The approximation subimage is obtained via downsampling from yLL(m,n). Then let
Finally, the decomposition mentioned above can transform any single-channel linear space-invariant filtering problem into a multichannel one [21, 22]. Transforming Eq.(2) into wavelet yields(9)
where and (o, p ∈ L,H) are subimages of and in wavelet domain and MTFqLL(u, v) is obtained from the wavelet transform of the step response function (SRF) of the system. Here the decomposition level in our study is 2.(10)
2.3 Inverse Problem: Phase Retrieval
The phase retrieval is required to obtain pronounced phase contrast of tomographic image for weakly absorbing samples. The phase contrast formation is closely related to a Laplacian operator in the transverse plan. The inverse of the Laplacian operator amplifies the low frequency information and the image noise, and suppresses high frequency counterparts, which can definitely give rise to image blurring when an impropriate phase retrieval algorithm is used. So the factors causing the blurring reconstructed image should be considered during not only the process of imaging formation, but also during the phase retrieval. Here we considered the single distance phase retrieval based on Transport of Intensity Equation (TIE) to improve the accuracy of TIE-based algorithm in our high resolution experiments.
2.3.1 Linearized Algorithm of Phase Retrieval
In order to retrieve a phase map for a given angular view, one should decode the phase information from the projections in the view by using the x-ray intensity transport equation. As is shown in [23, 24]
| (11) |
where λ is X-ray wavelength, D is the sample-to-detector distance, ID (x,y) denotes the projection X-ray intensity, Iin the entrance X-ray intensity. In Eq. (11) A2 (x,y) and φ(x,y) are the attenuation map and phase-shift map of the sample respectively, and M the magnification factor employed in the projection. Note that in this equation sin(λD∇2/4πM) and cos(λD∇2/4πM) are the two-dimensional pseudodifferential operators, in which operator ∇2 is the two-dimensional transverse Laplacian operator ∇2 ≡ (∂2/∂x2 + ∂2/∂y2). In mathematics the action on a function g (r⃗o) of a two-dimensional pseudo-differential operator O(c∇2) is defined as:
| (12) |
This general transport equation is the basis for developing phase retrieval methods. The X-ray transport equation (Eq. (11)) can be simplified in many applications where the so-called the maximal Fresnel propagator phase FPPM ≡ πλ DM / 4p2 is much less than 1, where p denote the pixel size of a detector. If an imaging setup employs a detector pixel size of tens micrometers and a sample-detector distances of few meters or less, then this imaging setup’s maximal Fresnel propagator phase FPPM << 1. Under the condition FPPM << 1, the sin(FPPM) and cos(FPPM) can well be linearized in terms of the transverse Laplacian operator ∇2, hence the general X-ray transport equation Eq. (11) can be reduced to
| (13) |
This simplified transport equation is the so-called Transport of Intensity Equation (TIE) in literature [25, 26]. Hence the task of phase retrieval is to extract the phase map ϕ(x,y) from phase contrast projections by using Eq. (11) or Eq. (13) if FPPM << 1. For sake of simplification,, here we consider the cases of illuminating a homogeneous object with an incident monochromatic plane X-ray wave (M=1). Absorption and refraction of X-rays of a given wavelength λ in a given material can be described with the complex refractive index n=1−δ+iβ, where the refractive index decrement δ and the imaginary part β and are responsible for the X-ray phase shift and attenuation respectively. Under the assumption of a homogeneous sample, the TIE of Eq. (13) gets simplified, and the simplified TIE equation is called TIE-homo equation. The TIE-homo-based phase retrieval can be written as [26]:
| (14) |
Here, the F{•} and F−1{•} are the forward and backward Fourier transform operators respectively. (u, v) is the Fourier conjugate coordinates of (x, y). Therefore, under the assumption of a homogeneous sample, the sample’s phase map can be retrieved from a single projection by using Eq. (14).
2.3.2 Generalized Algorithm of Phase Retrieval
For the high-resolution imaging discussed in Section 2.2, the FPPM is 1.34, sin(FPPM) = 0.97, cos(FPPM) = 0.97 respectively. For such high-frequencies, Eq. (14) may filter out too much high-frequency information as it should be, thereby it causes blurs. The theoretical advantage of using Eq. (11) rather than Eq. (13) is that Eq. (11) is applicable as well to the cases with FPPM ~ 1 or FPPM > 1, as is the case in our experiment [9]. Although Eq. (11) is more sophisticated than Eq. (13), we found that the phase map of a given view angle can be retrieved as:
| (15) |
Comparing Eq. (15) to Eq. (13), the key difference is that the phase retrieval operator in Eq. (15) is changed to a more convolved pseudo-differential operator . Note that the large value of the ratio δ / β reflects the high sensitivity of the phase contrast imaging. Using the definition of a general pseudo-differential operator, we can rewrite Eq. (15) in a more convenient form for computation:
| (16) |
Note that this equation will reduce to your Eq. (14) for the cases with FPPM << 1, as cosine and sine terms get linearized, and δ/β>>1.
2.4 Three Different PPCT Techniques
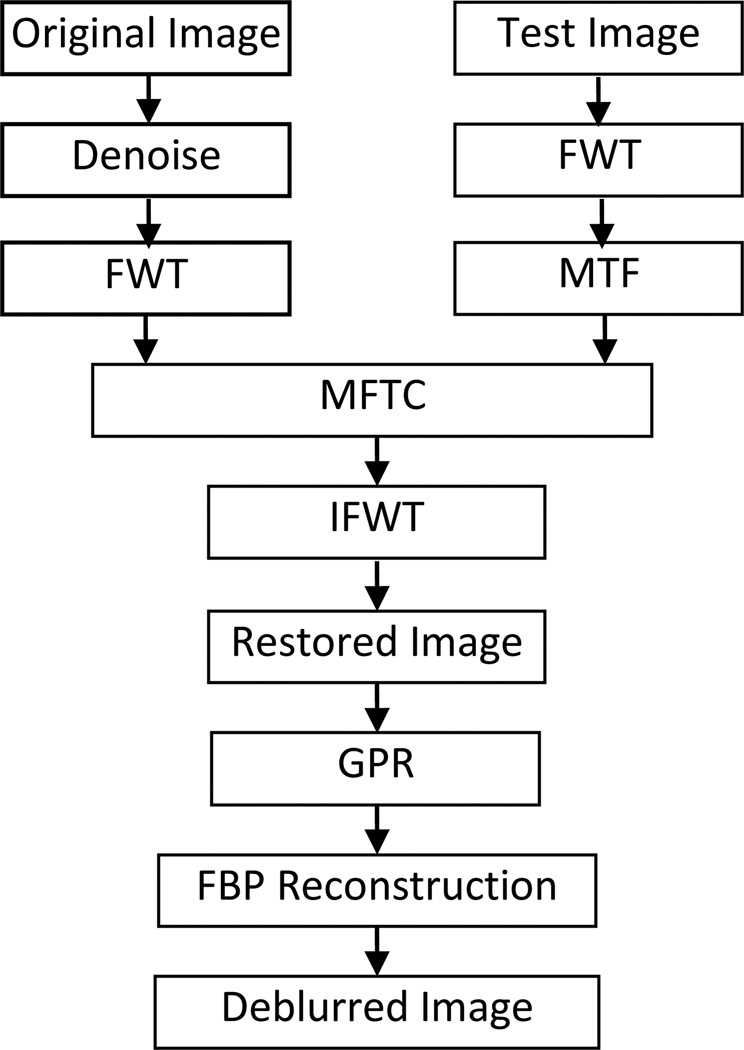
According to the above statement of our proposed principle, the procedures of the MTFC-GPR-based PPCT technique can be given in the Fig. 2.
Fig. 2.
Flowchart of the MFTC-GPR-based PPCT technique. FWT denotes the fast wavelet transform, IFWT denotes the inverse transform of FWT, MTFC represents the MTF compensation algorithm, and GPR represents the generalized phase retrieval algorithm.
For the sake of comparison, the projection data were conducted with three different reconstructed techniques, shown in Table. 1. Prior to FBP reconstruction, each raw image had been corrected by the dark current signal and flat-field-normalized. The direct PPCT tomograms are reconstructed directly from projection phase-contrast images, using the FBP algorithm. The reconstructed image is a map of the apparent linear attenuation coefficients (LACs). The image contrast mechanism of the direct PPCT is a mixture of the attenuation contrast and refraction contrast. The LPR-based PPCT with the phase retrieval based on Eq.(14) was applied to the phase contrast projection data and then reconstructed by FBP algorithm. The reconstructed image is a map of the sample’s δ values, or the map of electron densities. The image contrast can be enhanced greatly due to the high phase sensitivity ratio of δ/β for weakly absorbing materials. The MTFC-GPR-based PPCT based on the Eq.(10) and the Eq.(16), were employed to the phase contrast projections for solving the direct problem and inverse problem.
Table. 1.
Flowchart and comparison of Methods of PPCT
| Technique | Raw Image | Phase Retrieval | Reconstruction |
|---|---|---|---|
| Direct PPCT | ID/Iin | No | FBP |
| LPR-based PPCT | ID/Iin | Linearized PR | FBP |
| MTFC-GPR-based PPCT | MTFC {ID/Iin} | Generalized PR | FBP |
3. Results and Discussions
3.1 MTF measurement
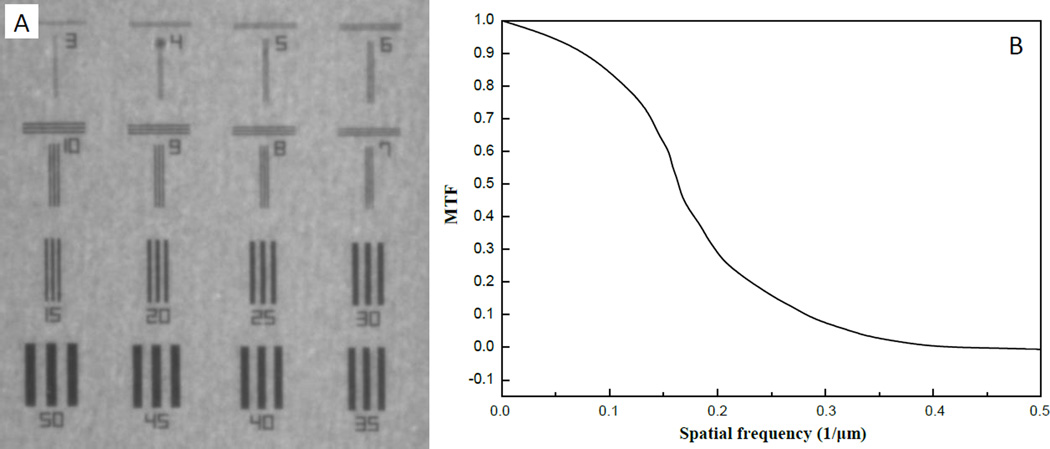
The modulation transfer function (MTF) was measured with a test-chart shown in Fig. 3(A), which is made of 1µm-thick of tantalum with electron lithography method by NTT-ATN, Japan. The conversion gain is about 4 Analogue-to-digital-converter (ADC) per an X-ray photon of 15keV. The MTF curve was estimated from the Fourier transform of the line spread function (LSF) of the knife edge response, fitted with an error function by means of a least-squares fit, as is shown in Fig. 3(B).
Fig. 3.
The measurement of MTF of the X-ray imaging system with the test chart at 15 keV. (A) Radiogram of test chart, and each number shows the pitch of line and space patterns which corresponding to spatial resolution. (B) the MTF from (A).
3.2 Standard PMMA Specimen
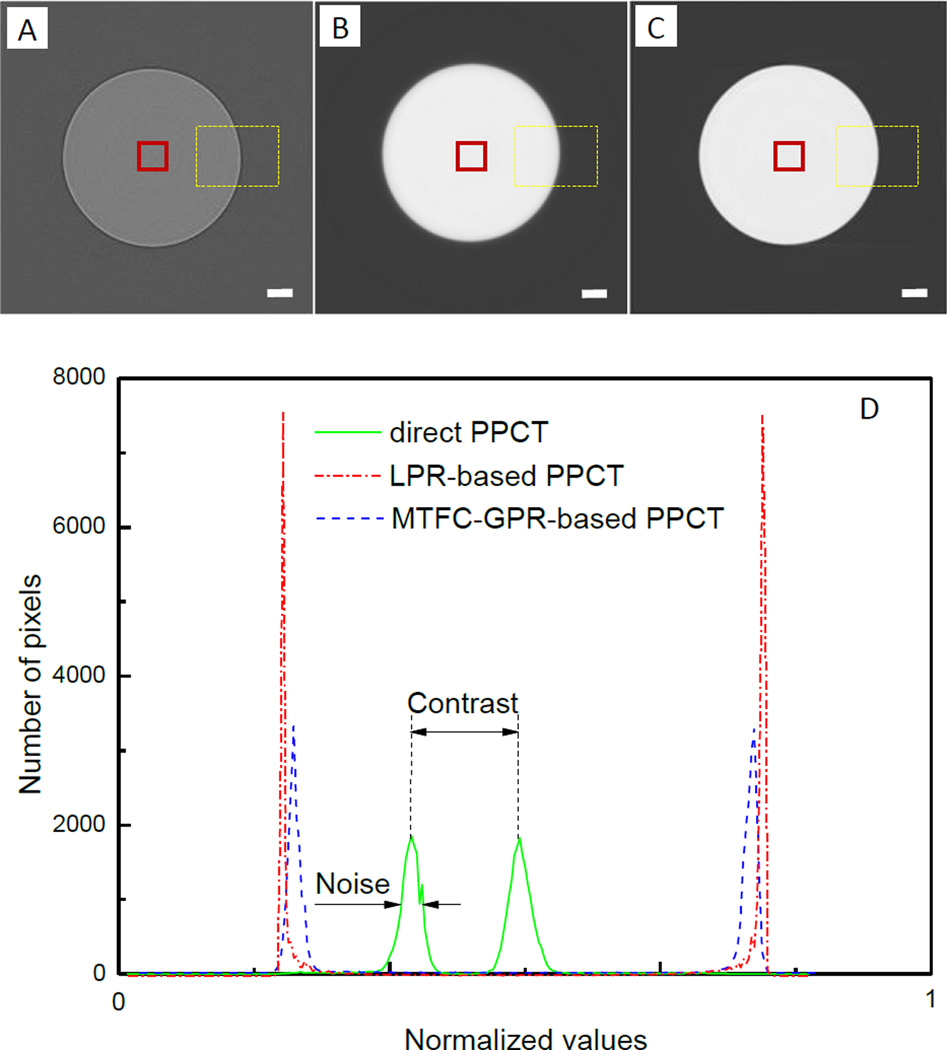
Fig. 4(A–C) are three images of the PMMA rod that were reconstructed from the same acquired projection dataset by using the three different PPCT techniques as described earlier. Fig. 4(A) shows the slice image reconstructed with the direct PPCT technique, featured with the edge enhancement at the boundary and weak contrast between the bulk areas of sample and background. Fig. 4(B) is the slice image reconstructed with the LPR-based PPCT technique, which displays the strong phase contrast without edge enhancement, but introduces significant blurring at boundaries. Fig. 4(C) is the slice image reconstructed with MTFC-GPR-based PPCT technique, which demonstrates the strong phase contrast and good sharpness simultaneously due to considering the direct and inverse problems. Fig. 4(D) shows the histograms of normalized reconstruction values using three different PPCT techniques, calculated from yellow dash-line regions in the Fig. 4(A–C) respectively. The full width of half maximum (FWHM) of the background peak denotes the noise level and the distance between the both peaks of PMMA and background reflects the contrast of image. It can be easily observed that the direct PPCT technique has relatively serious noise and weak contrast compared to the both phase-retrieval-based PPCT techniques. Although there are similar noises and contrasts in the both phase-retrieval-based PPCT techniques, the LPR-based PPCT seems to show a slightly better performance on contrast-to-noise ratio due to the inaccurate filtering function based on Eq.(14), which unduly suppress the high frequency components and mostly cause a blurring boundary as demonstrated in Fig. 4(B), partially including the spread function of imaging system. However, the MTFC-GPR-based PPCT technique accurately considers the negative factors affecting the both signal-to-noise ratio and sharpness of reconstructed results, especially being essential for the discrimination of tiny structures in biological samples. To evaluate the reconstructed accuracy quantitatively, the reconstructed values were examined in view of relative errors (RE), defined as the following formula [27]:
| (17) |
Fig. 4.
Tomographic Slices of the PMMA cylinder with direct PPCT (A), LPR-based PPCT (B), and MTFC-GPR-based PPCT (C); and (D) histograms of them in the corresponding ROIs marked with yellow dash-lines. The red solid-line ROIs used for calculating average reconstructed value. The length of scalar bar is 120µm.
For the standard PMMA, the ratio δ/β at 15keV is 1561. The average reconstructed values in the red squares indicated in the Fig. 3.(a–c) are that of the apparent LAC and refractive index decrements by using the three different PPCT. The average reconstructed values are 1.238 cm−1 for the direct PPCT, 1.348 × 10−6 for the LPR-based PPCT and 1.207 × 10−6for the MTFC-GPR-based PPCT, respectively. Compared with their theoretical values (μ=1.200 cm−1 and δ=1.190 × 10−6 at 15keV), the REs of the three PPCT techniques can be obtained respectively as following: 3.17%, 13.28% and 1.43%. The results shows the MTFC-GPR-based PPCT has the highest reconstruction accuracy due to the appropriate MTF compensation of imaging system and the accurate inverse filtering based on Eq.(16), while the LPR-PPCT has a relatively lower accuracy owing to the over-smoothing inverse filter based on Eq.(14) as in our experiment FPPM is as high as 1.34 and Eq. (14) is not applicable.
3.3. Biological Specimen
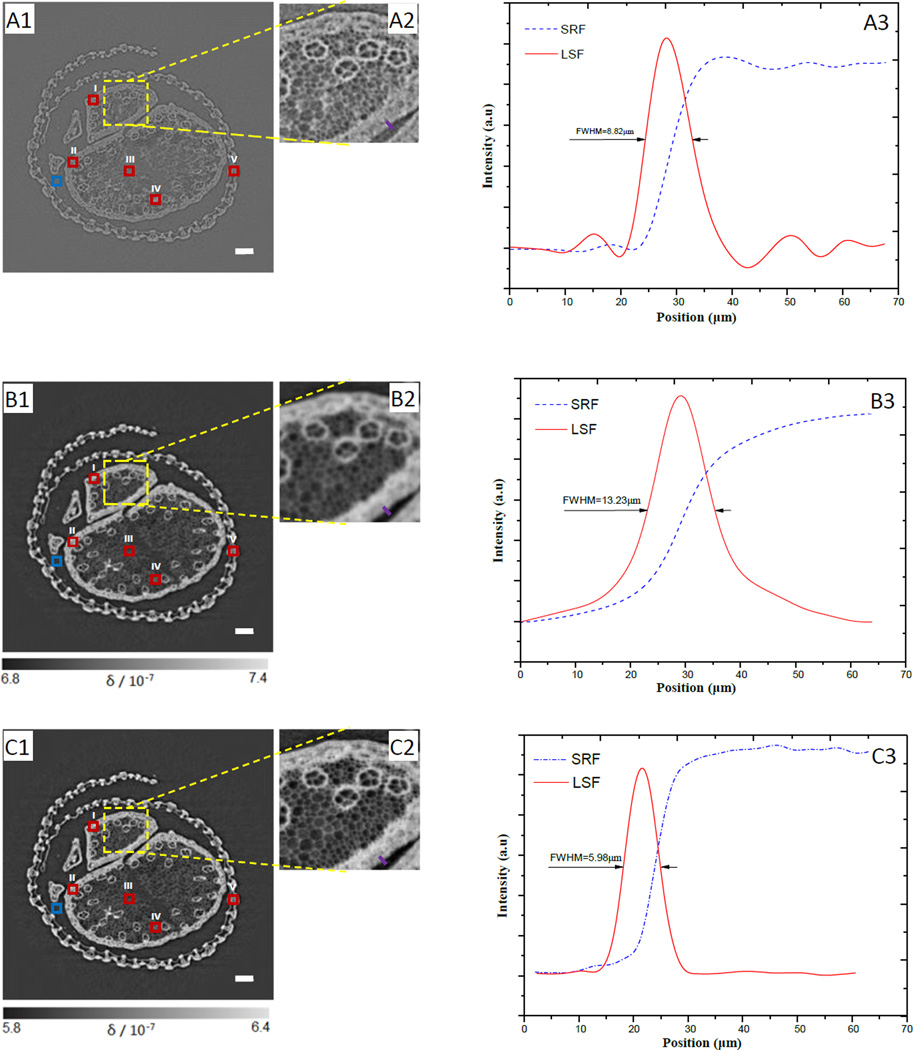
In order to evaluate the availability of the technique and compare image qualities of the three different techniques, the tomographic cross sections of the cordyceps sinensis specimens were reconstructed with the direct PPCT, the LPR-PPCT, and the MTFC-GPR-PPCT respectively. For phase reconstructions, the biological sample, mainly consisting of low-Z elements, has the density of about 0.9 g/cm3 via comparing with standard solutions. The sample's δ/β can be estimated as 1897 by referring to the method [28]. Viewing the experimental results, it can be obviously seen in the Fig. 5(A1–A2) that the sample's structural details are distinguished between different plant tissues due to the edge enhancement from the transmitted X-rays, and the contrasts between them are too weak to provide the useful means for the quantitative analysis and gray scale segmentation. The LPR-PPCT-based slices, shown in Fig. 5(B1–B2), appears the stronger bulk contrast attributed to the phase retrieval and an emerging undesirable problem, namely the various detailed features become blurred. This reveals ambiguities among plant tissues of tiny hyphae and void. This is mainly due to the removed edge enhancements by running a low-pass filter of inaccurate phase retrieval. Finally, the MTFC-GPR-based slices, seen in Fig. 5(C1–C2), clearly shows these various tissue details of subtle hyphaes and water ducts and meanwhile remains the pronounced phase contrast between the tissues and background ROIs, which demonstrate that the new PPCT technique has great potential for discrimination and characterization of biological structural information.
Fig. 5.
Tomographic slices of the biological sample with the direct PPCT (A1), PR-based PPCT (B1), and MTF-PR-based PPCT (C1) respectively, (A2), (B2) and (C2) are the partial enlarged views indicated with yellow solid-line squares correspondingly. The ROIs (I–V) defined with these red solid-line squares in sample's areas and a ROI defined with blue solid-line square in background are used for calculating CNR. The solid purple line plotted along an edge on the same position in (A2), (B2), and (C3) respectively, are used for measuring the step response function (SRF) and estimating their spatial resolution by calculating the FWHM of the line spread function (LSF), the corresponding results are shown in the (A3), (B3), and (C3), and the FWHMs are 8.82µm, 13.23µm, 5.98µm corresponding to direct PPCT, PR-based PPCT, and MTF-PR-based PPCT respectively. The length of the scale bar is 120µm.
Since the sharpness of an image is essential to observation of fine structures, the spatial resolution (SR) of the tomographic slices were estimated from a criterion based the full widths at half maximum (FWHM) of the LSF curves, which were derived from the SRF fitted with an error function by means of a least-squares fit [29]. In this way the image spatial resolution was determined by the FWHM of the LSF function. In order to quantitatively estimate the spatial resolutions for the three techniques, the LSF curves associated with the three techniques are measured as shown in Fig. 5 (A3), (B3), and (C3). From the LSF curves, we determined their FWHMs as 8.82µm, 13.23µm, and 5.98µm, corresponding to the direct PPCT, LPR-based PPCT, and MTFC-GPR-based PPCT techniques, respectively. For our experiment, compared in terms of these FWHM values, the MTFC-GPR-based techniques has more than twice sharper resolution than that of LPR-based technique, and more sharper than that of direct PPCT technique. This result explains the observation that among the three enlarged insets in Fig. 5, the Fig. 5 (C2) is sharpest to show the fine structures.
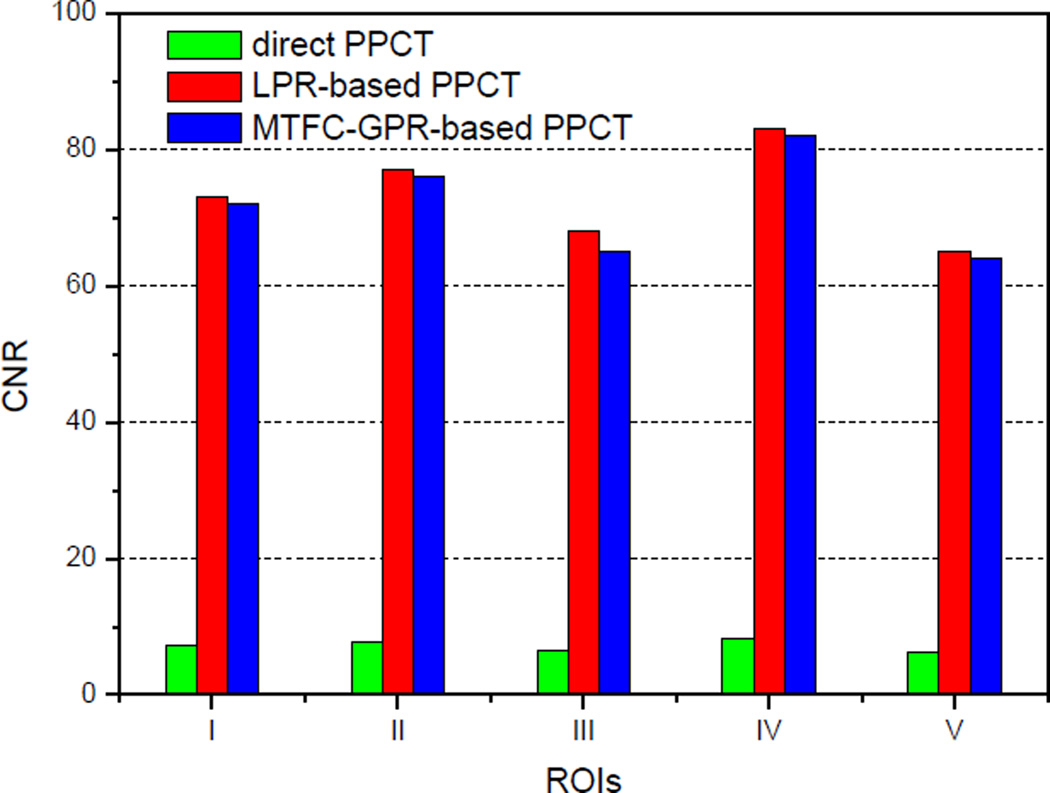
The reconstructed tomographic slices were examined in view of contrast-to-noise ratio (CNR), and the CNR formula was defined as the following [30]:
| (18) |
where Si and σi represents mean pixel values and standard deviations, and the subscribe i means the region of interest (ROI) of the object and background, depicted with the red and blue solid-line squares in Fig. 5(A1), (B1) and (C1) respectively. For reliable consideration, there are multiple ROIs (I–V), locating at various tissue areas, were employed to calculate the CNRs. The measured CNRs form the three tomograms in Fig. 5(A1), (B1) and (C1), reconstructed with the three different PPCT techniques, are shown in the Fig. 6. It can be clearly seen that both the phase-retrieval-PPCT techniques achieved almost 10 times higher CNRs than that with the direct-PPCT technique, which demonstrate the phase retrieval has great potential for both suppressing noise and enhancing the image contrast compared to the direct PPCT. The measured results also show that the LPR-based PPCT technique has slightly higher CNRs than that with the MTFC-GPR-based PPCT technique. However, the LPR-based PPCT would unduly suppress the high frequency components of the projection dataset and cause the serious losses in spatial resolution, when it is applied to high-resolution angular projections with FPPM ≥1, such as the case in our experiment. This is why the increase of the CNRs with the LPR-based PPCT is accompanied with serious blurring as is demonstrated in Fig. 5 (B2).
Fig. 6.
The comparisons of CNRs estimated form the multiple ROIs defined in Fig.5 (A1), (B1) and (C1).
Generally speaking, there always is a trade-off relationship between spatial resolution and CNR for improving the image quality. We have found that the MTFC-GPR-based PPCT technique has not only exhibited the higher spatial resolution, but also exhibited the high CNR in our comparison study. The experimental results indicate that our presented method has potential interest for the optimization of PPCT technique with phase retrieval for biomedical applications.
5. Conclusion
In summary, we investigated the validity and advantages of the MTFC-GPR-based PPCT technique by considering the problems of both imaging formation and phase retrieval. The MTF compensation algorithm based on the wavelet transform and the modified phase retrieval were effectively applied to the high-resolution imaging tasks such as those with FPPM ≥1. Our experimental results indicated that the novel technique is superior to the LPR-based PPCT technique in fine structure discrimination and characterization. In a comparison to the direct PPCT technique, our experiment demonstrated striking CNR-enhancement with this novel technique. Hence the MTFC-GPR-based PPCT will be useful to visualize the fine structures such as voids, fibers, lesions in soft material and biomedical specimens, particularly for those applications that require high spatial resolution but meanwhile are subject to stringent radiation dose constraints.
Acknowledgements
The authors acknowledge the Japan Synchrotron Radiation Research Institute (JASRI) for helpful assistance with operating SPring-8 facility. X.Z Wu was supported in part by the US NIH grant Nos. R01CA142587 and R01CA193378. T.Q Xiao was supported by the National Natural Science Foundation of China (Grant No. 11105213).
References
- 1.Sera T, Uesugi K, Yagi N. Refraction-enhanced tomography of mouse and rabbit lungs. Med. Phys. 2005;32(9):2787–2792. doi: 10.1118/1.2008429. [DOI] [PubMed] [Google Scholar]
- 2.Lewis RA, Hall CJ, Hufton AP, Evans S, Menk RH, Arfelli F, Rigon L, Tromba G, Dance DR, Ellis IO, Evans A, Jacobs E, Pinder SE, Rogers KD. X-ray refraction effects: application to the imaging of biological tissues. The British Institute of Radiology. 2003;76:301–308. doi: 10.1259/bjr/32889803. [DOI] [PubMed] [Google Scholar]
- 3.Zhang Da, Donovan Molly, Fajardo Laurie L, Archer Ann, Wu Xizeng, Liu Hong. Preliminary Feasibility Study of an In-line Phase Contrast X-Ray Imaging Prototype. IEEE TRANSACTIONS ON BIOMEDICAL ENGINEERING. 2008;55(9):2249–2257. doi: 10.1109/TBME.2008.919136. [DOI] [PubMed] [Google Scholar]
- 4.Cloetens P, Ludwig W, Baruchel J, Van Dyck D, Van Landuyt J, Guigay JP, Schlenker M. Holotomography: Quantitative phase tomography with micrometer resolution using hard synchrotron radiation X-rays. Appl. Phys. Lett. 1999;75:2912. [Google Scholar]
- 5.Kitchen MJ, Lewis RA, Yagi N, Uesugi K, Paganin D, Hooper SB, Adams G, Jureczek S, Singh J, Christensen CR, Hufton AP, Hall CJ, Cheung KC, Pavlov KM. Phase contrast X-ray imaging of mice and rabbit lungs: a comparative study. The British Institute of Radiology. 2005;78:1018–1027. doi: 10.1259/bjr/13024611. [DOI] [PubMed] [Google Scholar]
- 6.Gureyev TE, Mayo SC, Myers DE, Nesterets Ya, Paganin DM, Pogany A, Stevenson AW, Wilkins SW. Refracting Rontgen's rays: Propagation-based X-ray phase contrast for biomedical imaging. J. Appl. Phys. 2009;105 102005-(1–17) [Google Scholar]
- 7.Liu Y, Nelson J, Holzner C, Andrews JC, Pianetta P. Recent advances in synchrotron-based hard X-ray phase onctrast imaging. J. Phys. D: Appl. Phys. 2013;46:494001. [Google Scholar]
- 8.Wu Xizeng, Liu H, Yan A. Phase-contrast X-ray tomography: Contrast mechanism and roles of phase retrieval. EJR. 2008;68S:S8–S12. doi: 10.1016/j.ejrad.2008.04.027. [DOI] [PubMed] [Google Scholar]
- 9.W X, Y A. Phase retrieval from one single phase contrast x-ray image. Opt. Express. 2009;17:11187–11196. doi: 10.1364/oe.17.011187. [DOI] [PubMed] [Google Scholar]
- 10.Groso A, Abela R, Stampanoni M. Implementation of a fast method for high resolution phase contrast tomography. Opt. Express. 2006;14:8103–8110. doi: 10.1364/oe.14.008103. [DOI] [PubMed] [Google Scholar]
- 11.Gureyev TE, Paganin DM, Myers GR, Nesterets Ya I, Wilkins SW. Phase-and-amplitude computer tomography. Appl. Phys. Lett. 2006;89:034102. [Google Scholar]
- 12.Liu H, Ren Y, Guo H, Xue Y, Xie H, Xiao T, Wu X. Phase retrieval for hard X-ray computed tomography of samples with hybrid compositions. Chin. Opt. Lett. 2012;10:121101. doi: 10.3788/COL201210.121101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Weitkamp T, Haas D, Wegrzynek D, Rack A. ANKAphase: software for single-distance phase retrieval from inline X-ray phase-contrast radiographs. J. Synchrotron Rad. 2011;18:617–629. doi: 10.1107/S0909049511002895. [DOI] [PubMed] [Google Scholar]
- 14.Langer M, Cloetens P, Peyrin F. Regularization of phase retrieval with phase-attenuation duality prior for 3-D Holotomography. IEEE Trans. Image Process. 2010;19(9):2428–2436. doi: 10.1109/TIP.2010.2048608. [DOI] [PubMed] [Google Scholar]
- 15.Wu, Liu H, Yan A. X-ray phase-attenuation duality and phase retrieval. Opt. Lett. 2005;30:379–381. doi: 10.1364/ol.30.000379. [DOI] [PubMed] [Google Scholar]
- 16.Burvall Anna, Lundstrom Ulf, Takman Per AC, Larsson Daniel H, Hertz Hans M. Phase retrieval in X-ray phase-contrast imaging suitable for tomography. Opt. Express. 2011;19(11):10359–10376. doi: 10.1364/OE.19.010359. [DOI] [PubMed] [Google Scholar]
- 17.Guigay JP, Langer M, Boistel R, Cloetens P. Mixed transfer function and transport of intensity approach for phase retrieval in the Fresnel region. Opt. Lett. 2007;32:1617–1619. doi: 10.1364/ol.32.001617. [DOI] [PubMed] [Google Scholar]
- 18.Neelamani R, Choi H, Baraniuk R. Fourier-wavelet regularized de-convolution for ill-conditioned system. IEEE Trans. Image Process. 2004;52(2):418–433. [Google Scholar]
- 19.Wang Z, Geng Z, Zhang Y, Sui X. The MTF measurement of remote sensors and image restoration based on wavelet transform; Proceedings of International Conference on Wavelet Analysis and Pattern Recognition (IEEE, Beijing); 2007. pp. 1921–1924. [Google Scholar]
- 20.Mallat SC. A theory for multi-resolution signal decomposition: the wavelet representation. IEEE Trans. Pattern Anal. Mach. Intell. 1989;11(7):674–396. [Google Scholar]
- 21.Samei E, Flynn MJ, Reimann DA. A method for measuring the pre-sampled MTF of digital radiographic systems using an edge test device. Med. Phys. 1998;25(1):102–113. doi: 10.1118/1.598165. [DOI] [PubMed] [Google Scholar]
- 22.Banham MR, Galatsanos NP, Gonzalez HL, Katsaggelos AK. Multichannel restoration of single channel images using a wavelet-based sub-band decomposition. IEEE Trans. Image Process. 1994;3(6):821–833. doi: 10.1109/83.336250. [DOI] [PubMed] [Google Scholar]
- 23.Wu X, Liu H. A general formalism for X-ray phase contrast imaging. Journal of X-ray Science and Technology. 2003;11:33–42. [PubMed] [Google Scholar]
- 24.Wu X, Liu H. A recontruction formula for soft tissue X-ray phase tomography. J. X-ray Sci. Technol. 2004;12:273–279. [Google Scholar]
- 25.Gureyev TE, Mayo SC, Nesterets Ya I, Mohammadi S, Lockie D, Menk RH, Arfelli F, Pavlov KM, Kitchen MJ, Zanconati F, Dullin C, Tromba G. Investigation of the imaging quality of synchrotron-based phase-contrast mammographic tomography. J. Phys. D: Appl. Phys. 2014;47:365–401. [Google Scholar]
- 26.Paganin D, Mayo SC, Gureyev TE, Miller PR, Wilkins SW. Simultaneous phase and amplitude extraction from a single defocused image of a homogeneous object. J. Microscopy. 2002;206:33–40. doi: 10.1046/j.1365-2818.2002.01010.x. [DOI] [PubMed] [Google Scholar]
- 27.Gureyev TE, Nesterets Yakov I, de Hoog Frank, Schmalz Gerd, Mayo Sheridan C, Mohammadi Sara, Tromha Giuliana. Duality between noise and spatial resolution in liner systems. Opt. Express. 2014;22(8):9087–9094. doi: 10.1364/OE.22.009087. [DOI] [PubMed] [Google Scholar]
- 28.Chen RC, Xie HL, Rigon L, Castelli E, Xiao TQ. Phase retrieval in quantitative x-ray microtomography with a single sample-to-detector distance. Opt. Lett. 2011;36:1719–1721. doi: 10.1364/OL.36.001719. [DOI] [PubMed] [Google Scholar]
- 29.Lovric Goran, Barre Sebastien F, Schittny Johannes C, Kleiner Matthias R, Mokso Rajmund. Dose optimization approach to fast X-ray microtomography of the lung alveoli. J. Appl. Cryst. 2013;46 doi: 10.1107/S0021889813005591. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Kitchen MJ, Paganin D, Lewis RA, Yagi N, Uesugi K. On the origin of speckle in X-ray phase contrast images of lung tissue. Phys. Med. Biol. 2004;49:4335–4348. doi: 10.1088/0031-9155/49/18/010. [DOI] [PubMed] [Google Scholar]