Cell type- and activity-dependent extracellular correlates of intracellular spiking

Abstract

Despite decades of extracellular action potential (EAP) recordings monitoring brain activity, the biophysical origin and inherent variability of these signals remain enigmatic. We performed whole cell patch recordings of excitatory and inhibitory neurons in rat somatosensory cortex slice while positioning a silicon probe in their vicinity to concurrently record intra- and extracellular voltages for spike frequencies under 20 Hz. We characterize biophysical events and properties (intracellular spiking, extracellular resistivity, temporal jitter, etc.) related to EAP recordings at the single-neuron level in a layer-specific manner. Notably, EAP amplitude was found to decay as the inverse of distance between the soma and the recording electrode with similar (but not identical) resistivity across layers. Furthermore, we assessed a number of EAP features and their variability with spike activity: amplitude (but not temporal) features varied substantially (∼30–50% compared with mean) and nonmonotonically as a function of spike frequency and spike order. Such EAP variation only partly reflects intracellular somatic spike variability and points to the plethora of processes contributing to the EAP. Also, we show that the shape of the EAP waveform is qualitatively similar to the negative of the temporal derivative to the intracellular somatic voltage, as expected from theory. Finally, we tested to what extent EAPs can impact the lowpass-filtered part of extracellular recordings, the local field potential (LFP), typically associated with synaptic activity. We found that spiking of excitatory neurons can significantly impact the LFP at frequencies as low as 20 Hz. Our results question the common assertion that the LFP acts as proxy for synaptic activity.

monitoring activity in the living brain in vivo has traditionally been performed via extracellular voltage (V_e) recordings through single wires, wire bundles (for example, tetrodes; Gray et al. 1995), and, more recently, high-density silicon probes (Csicsvari et al. 2003; Buzsáki 2004; Patel et al. 2006; Du et al. 2009) used to detect action potential (spike) signals originating from transmembrane currents of neurons mediated through the conductive extracellular medium. While such V_e recordings have played a pivotal role in our understanding of circuit processing and computation, many questions still remain about events and processes related to these signals. For example, how do spatiotemporal features of the extracellular action potential (EAP) waveform change as a function of distance to the recording site, spike pattern, or cell type? What are the physical properties of the medium separating a neuron from an extracellular site? How do space- and time-dependent features of the EAP signature manifest themselves in the V_e recording? In the past, it has been difficult to address such questions mainly due to methodological challenges: voltage recording within, across, and outside neural compartments within a few tens of micrometers from multiple recording sites is a nontrivial task. The few pioneering studies that did so typically recorded V_e from a proximal wire (Amzica and Steriade 2000) or wire-bundle electrode (Henze et al. 2000), limitations that largely reduced analyses to temporal aspects of spiking and EAPs.

Understanding the spatial scale of events such as EAP initiation and propagation across the extracellular medium is crucial towards understanding V_e signals and what these represent. For example, what is the sampling volume of an extracellular electrode? In the past, various distances have been suggested ranging from a few tens to hundreds of micrometers (Henze et al. 2000; Gold et al. 2006; Pettersen and Einevoll 2008; Schomburg et al. 2012). Beyond spatial sampling, V_e recordings, and EAP waveforms in particular, are highly space- and time-dependent, posing significant challenges to physiologists attempting to attribute specific EAP shapes and features to individual neurons (so-called units), a process often referred to as spike sorting. One way to increase sorting reliability is through multiple, spatially proximal, recording sites recording from the same neuron with single-neuron recorded EAP waveforms being different (but temporally tightly coherent) across sites (Gray et al. 1995). Hitherto the origin and degree of EAP waveform variability from a single neuron as function of experiment-, cell type-, and spike history-specific parameters remain largely unknown (Hill et al. 2011). In summary, it has been hard to bridge single-neuron, single-compartment intracellular and transmembrane physiology with extracellular signals as these are typically measured in vivo.

Traditionally, biophysical studies of EAP generation and recording are separated in two groups: first, the ones characterizing the neural origin of EAPs in terms of intracellular and transmembrane conductances contributing to these signals, and second, those characterizing the physical properties of the extracellular medium that crucially impacts EAP features. To characterize the origin of EAPs, intracellular in vivo recordings have been performed (Buzsáki et al. 1996; Henze et al. 2000) (using intracellular sharp electrodes) while computational modeling has played a crucial role in bridging the gap between transmembrane events and extracellular signals (Gold et al. 2006; Pettersen and Einevoll 2008; Schomburg et al. 2012; Reimann et al. 2013; Anastassiou et al. 2013). Notably, the wide majority of computational models studying EAPs typically assume a homogeneous, purely resistive extracellular medium. Regarding characterization of the physical properties of the extracellular medium, hitherto, measurements of extracellular conductivity have been performed with various experimental setups such as metal wires (Ranck 1963), microstimulation electrodes (Logothetis et al. 2007; Goto et al. 2010), glass pipettes (Histed et al. 2009), parallel plates (Deans et al. 2007), etc. While these pioneering studies have provided insights into the conductivity of the extracellular space, very few studies have attempted to address this question using the main generator of electrogenesis in the brain, the neuron itself. The neuron as a current source for such measurements poses a unique challenge: physiologically, neural signals can vary substantially so that the current source is not as stereotyped as current injections from specialized hardware and, technically, because intracellular and extracellular stimulation and recordings need to be performed in close proximity as EAP signals rapidly decay within a few tens of micrometers from the soma (Henze et al. 2000; Buzsáki 2004). Yet, neurons give rise to inherently nonlinear, local, and transient subthreshold and spike responses, and EAP waveforms naturally follow that pattern casting EAP and extracellular medium characterization in the absence of actual neurons problematic.

MATERIALS AND METHODS

Slice preparation and cell identification.

Fourteen- to eighteen-day-old Wistar rats were quickly decapitated according to the Swiss Welfare Act and the Swiss National Institutional Guidelines on Animal Experimentation for the ethical use of animals. The project was approved by the Swiss Cantonal Veterinary office following its ethical review by the State Committee for Animal Experimentation. The brain was carefully removed and placed in iced artificial cerebrospinal fluid (ACSF). The 300-μm-thick parasagittal slices of the primary somatosensory cortex (hindlimb area) were cut on a HR2 vibratome (Sigmann Elektronik, Heidelberg, Germany). Experiments were performed at room temperature (to minimize electromagnetic interference). Cells were visualized by infrared differential interference contrast video microscopy utilizing a VX55 camera (Till Photonics, Gräfelfing, Germany) mounted on an upright BX51WI microscope (Olympus, Tokyo, Japan). Care was taken to use only “parallel” slices, i.e., slices that had a cutting plane parallel to the course of the apical dendrites and the primary axonal trunk. This ensured a sufficient preservation of both the neuron's axonal and dendritic arborizations.

Chemicals and solutions.

Slices were continuously superfused with ACSF containing the following (in mM): 125 NaCl, 25 NaHCO₃, 2.5 KCl, 1.25 NaH₂PO₄, 2 CaCl₂, 1 MgCl₂, and 25 d-glucose, bubbled with 95% O₂-5% CO₂. The intracellular pipette solution contained the following (in mM); 110 K-gluconate, 10 KCl, 4 ATP-Mg, 10 phosphocreatine, 0.3 GTP, 10 HEPES, and 13 biocytin, adjusted to a pH 7.3–7.4 with 5 M KOH. Osmolarity was adjusted to 290–300 mosM with d-mannitol (25–35 mM). The membrane potential values given were not corrected for the liquid junction potential, which was approximately −14 mV. Some experiments were performed under 20 μM SR 95531 hydrobromide (Gabazine; Tocris) to block inhibition and give rise to more spiking in the slice, yet we observed no impact in terms of EAP waveform features. Thus results presented herein are from experiments without any synaptic receptor blockers.

Intracellular whole cell patch-clamp stimulation and recordings.

Multiple somatic whole cell stimulation and recordings (1–4 cells simultaneously) were performed with Multiclamp 700B amplifiers (Molecular Devices, Union City, CA) in the current-clamp mode. The reference electrode in all experiments was positioned ∼1 cm from the slice in the ACSF bath in order not to be affected by the extracellular stimulus. Bridge balance compensation was continuously performed during all recordings. Data acquisition was performed via an ITC-1600 board (Instrutech, Port Washington, NY), connected to a personal computer running a custom written routine under IgorPro (Wavemetrics, Portland, OR). Sampling rate was 10 kHz. Patch pipettes were pulled with a Flamming/Brown micropipette puller (DMZ Universal Puller; Zeitz-Instrumente, Munich, Germany) and had an initial resistance of 4–8 M. Three-dimensional morphological reconstruction of biocytin-labeled cells was done under an Olympus BX 51W microscope fitted with a water-immersion ×60 [numerical aperture (NA) 0.9] or an oil-immersion ×100 (NA 1.35) objective using Neurolucida software (MicroBrightField, Magdeburg, Germany).

Extracellular recordings.

The 4-shank, 32-site (B32) NeuroNexus (Ann Arbor, MI) silicon probe was attached to one of the micromanipulators and moved slowly to the target. Each shank had eight recording sites (160 μm² each site, 1–3 MΩ impedance), and intershank distance was 200 μm. Recordings sites were staggered to provide a two-dimensional arrangement (20-μm vertical staggered separation). Before experiments, the silicon probe was inserted in a 5% tripsin solution for ∼60–120 min for cleaning purposes. Upon insertion of the silicon probe into the slice, a waiting period of ∼30–45 min allowed for the neurons closest to the shanks to settle in position. Whole cell patch-clamp recordings were then performed around the probe. Data were acquired using a 32-channel Plexon (Houston, TX) wideband amplifier with sampling frequency of 10 kHz and 1,000-fold amplification. Distance along the tissue depth axis between soma (intracellular site) and extracellular sites along the shank was determined via z-stacks (spacing: 1 μm). Euclidean distance between soma and each shank site was then calculated based on the distance from two landmarks, the silicon probe tip and the top edge. The soma location was taken as the center of the soma of the patched neuron in the x–y plane of the depth where the soma appeared largest.

Theory and modeling.

The compartment model used (see Fig. 3) was developed by Hay et al. (2011), and we adopted it from the NEURON database. Briefly, the authors used an automated feature-based parameter search to faithfully replicate elicitation of somatic Na⁺ spikes in response to a prolonged step current, the generation of a Ca²⁺ spike at the distal apical dendrites, as well as the interaction between the two spiking zones via the backpropagating firing. For a given modeled L5b pyramidal neuron morphology, the optimization-algorithm provided a set of acceptable models (and consequently a range of model parameters) that faithfully replicate the target experimental results, as well as exhibiting the experimental variability. Experimental studies have shown that numerous such combinations of ion channel densities can result in similar firing behavior. Our simulations were performed using the NEURON software package (version 7.3). To account for the extracellular recordings sites we assumed a purely resistive extracellular medium of 2.5-m resistivity with the location of the extracellular sites emulating that of an actual H32 shank (confirmed via visual inspection).

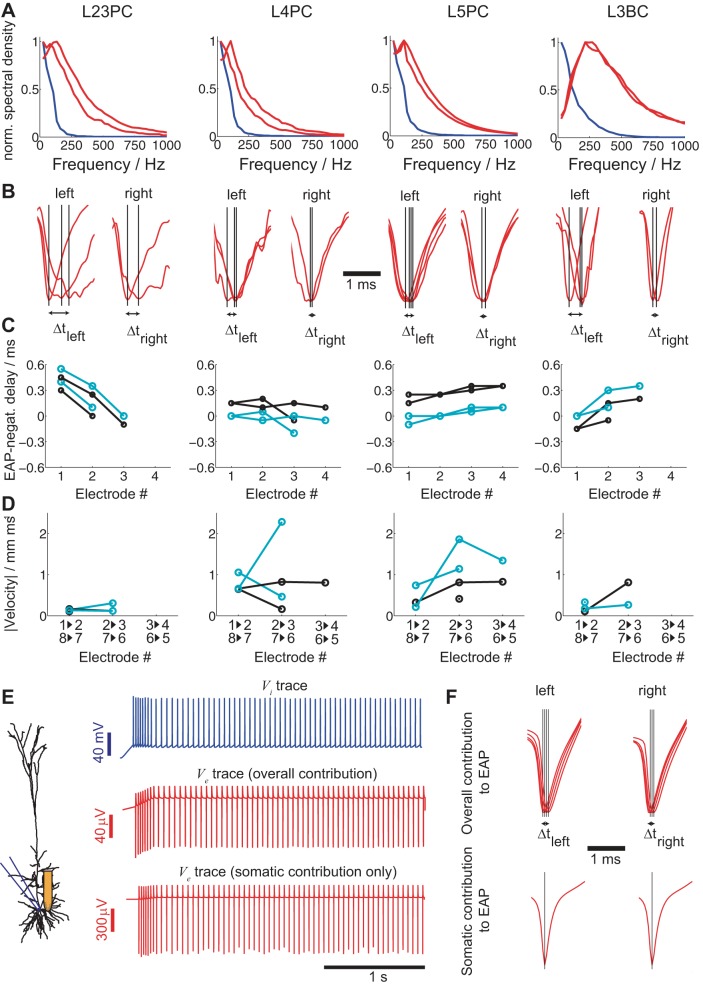
Fig. 3.

Temporal characteristics of EAP signals from identified single neurons. A: frequency spectra of intracellular spikes (blue lines) and the 2 largest EAPs (red lines) of the 4 neurons shown in the figure. B: alignment of the mean EAP signals from the 8 sites along the silicon shank closest to the cell body to the spike initiation time t_spike (determined intracellularly) reveals temporal differences between the EAP signals (left to right). C: time difference between the EAP minimum at different sites along the same shank and the intracellular spike onset (black) or the time of the EAP negativity of the electrode recording the strongest EAP (cyan). The 2 shank sides are considered separately (see Fig. 2, A–D, 2nd and 3rd columns), hence the multiple lines (x-axis: electrode number as defined in Fig. 2A). D: signal-propagation velocity v calculated from the interelectrode distances (x-axis: electrodes involved in calculation of v). AP minima delays are attributed to somatic APs traveling back along the apical dendrites (see text). E: same intracellular input as in Fig. 1 delivered to the soma of a L5 pyramidal neuron simulation (see materials and methods) with extracellular recording sites positioned at the same locations as for the silicon probe (left) and the resulting intra (top)- and extracellular responses (middle and bottom). V_e at a site 30 μm from the soma is either computed by taking into consideration the entire neuron (middle) or only the soma (bottom). F: if the same analysis as in B is carried out for the simulated data, the temporal differences between the EAP signals along the same shank can be attributed to membrane currents along the whole neural morphology (top). (Notably, the EAP delay and propagation speed are very similar to the ones measured experimentally for the L5 pyramidal neuron in B and C.) An identical simulation with only somatic compartments contributing to the EAP reveals no temporal differences (bottom).

Simulated extracellular activity (see Fig. 7, C–E) was generated using 37-ms-long EAP signatures around spike initiation time (determined intracellularly) from recorded cells summed with a lognormal spike-time distribution with a coefficient of variation (COV) of 0.5 and mean-firing frequencies of 1, 8, and 30 Hz for individual cells. Simulations involving eight cells simultaneously active (see Fig. 7, I–K) used mean-firing frequencies of 1, 4, and 12 Hz per cell to obtain multiunit activity (MUA) of 8, 32, and 96 Hz, respectively. Extracellular recordings from channels that did not record spiking [assessed by a flat spike-triggered average (STA) response] were used to test if extracellularly recorded action potentials produced significant changes to the extracellular signals. Two sample paired t-tests were performed for 30 different frequencies at 5-Hz intervals from 2 to 147 Hz, and Bonferroni correction for multiple comparisons was applied to 1% significance levels.

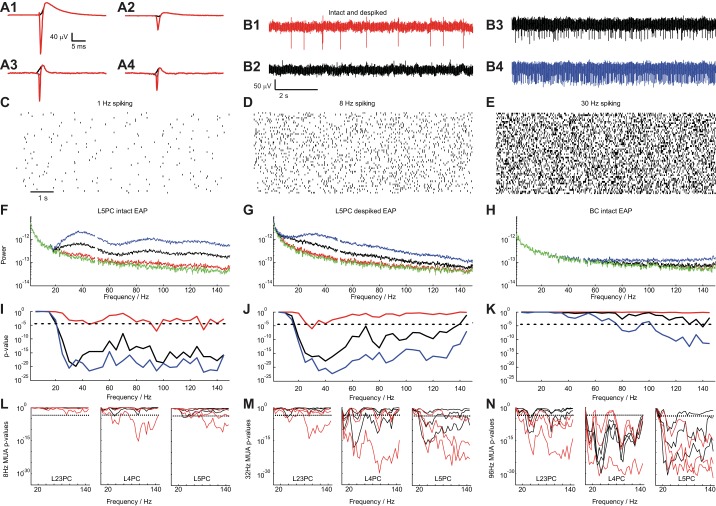
Fig. 7.

Impact of EAPs on the local field potential. A: spike-triggered EAP waveform of a L5PC (A1 and A2) and a L3BC (A3 and A4) (left: from site with largest EAP amplitude; right: from site recording the 2nd largest EAP waveform). The intact EAP waveform is shown (red) as well as the “de-spiked” one where the EAP negativity is missing (black; window of 0.6 ms around spike initiation time is substituted by a spline). B: extracellular traces composed using the L5PC EAP waveform: mean spike rate f₀ of 1 Hz with intact waveform (B1), 1 Hz with de-spiked waveform (B2; from A2), 8 Hz (B3), and 30 (B4) Hz with intact waveform. C–E: 50 realizations of a random process (log-normal PDF used to produce the ISI distributions) to create 9-s traces with f₀ = 1, 8, and 30 Hz, respectively. F: mean spectral density as a function of temporal frequency for the intact EAP waveform shown in A1 (green: no spiking; red: 1 Hz; black: 8 Hz; blue: 30 Hz). G: same as in F for the de-spiked EAP waveform of the L5PC shown in A1 (black). H: same analysis as in F for the intact EAP waveform of the basket cell shown in A3 (red). I–K: P value (t-test) for the pairwise comparison of spectral density at f₀ = 1 (red), 8 (black), and 30 Hz (blue) with no spiking (broken lines: P = 10⁻³, Bonferroni corrected) for the cases shown in F–H. L–N: same analyses introduced in I–K but instead of using the EAP waveform of a single neuron we use EAP waveforms from all neurons of a particular cell type (8 L23, 4 L4, and 12 L5 pyramidal neurons) to create extracellular voltage traces (as the ones shown in B) to emulate multiunit activity (MUA) with mean spike frequency f_MUA= 8, 32, and 96 Hz. Statistical significance (t-test, dashed line: P = 10⁻³, Bonferroni corrected) of the difference in spectral power between control (no spiking) and spiking traces at different frequencies for intact (red) and de-spiked (black) EAP waveforms. Lines of the same color show the result from different EAP waveforms as measured by different sites along the shank by considering the strongest and 2nd and 3rd strongest EAP signals both for the intact and de-spiked EAP waveforms with the lowest P value obtained for strongest EAP waveforms. For f_MUA equal or larger than 32 Hz, intact as well as de-spiked waveforms of all pyramidal cell types significantly impact spectral density as low as 20 Hz.

RESULTS

Intra- and extracellular action potentials.

To simultaneously monitor intracellular and extracellular voltages at multiple locations around identified neurons we modified a 12-pipette experimental setup (Anastassiou et al. 2011; Perin et al. 2011) by doing away with 1 of the pipettes and mounting a 4-shank/32-electrode silicon probe (8 electrodes per shank with staggered layout and interelectrode distance of 20 μm; see materials and methods) on one of the manipulators (Fig. 1). Such silicon probes have typically been used in hippocampal and neocortical recordings in vivo (Mizuseki et al. 2009, 2011; Mizuseki and Buzsáki 2013). In principle, this arrangement allowed us to position the silicon probe inside the slice at various orientations, i.e., horizontal or perpendicular to the somatodendritic axis of individual neurons (for example, compare Fig. 1, A with, B–D). Yet, for the majority of experiments we positioned the silicon probe parallel to the somatodendritic axis as typically done in vivo. Subsequently, using up to six pipettes, we approached neurons in close proximity to the silicon probe shanks and performed whole cell patch-clamp experiments. At the beginning of each experiment we applied a cell characterization protocol to determine cell properties such as input resistance and capacitance (Druckmann et al. 2011). Upon completing cell characterization, we injected 9-s intracellular DC current stimuli I_inj in steps of varying strength, from weak (“weak stimulation” in Fig. 1) to strong (“strong stimulation” in Fig. 1), to elicit spiking at different frequencies while simultaneously recording the intracellular voltage from the somatic patch-clamp pipette (blue traces in Fig. 1) and the extracellular voltage (red traces in Fig. 1) from different locations along the silicon probe (wideband signal was recorded, no filtering was performed). We did so for different neurons and layers of rat somatosensory cortex (hindlimb area): herein we present our findings for L23, L4, and L5 pyramidal neurons as well as basket cells. The cell type was established by combining cell-characterization findings and morphological reconstruction (Fig. 1; black lines: dendritic arbor; red lines: axon; location of the silicon probe shanks is also designated).

Fig. 1.

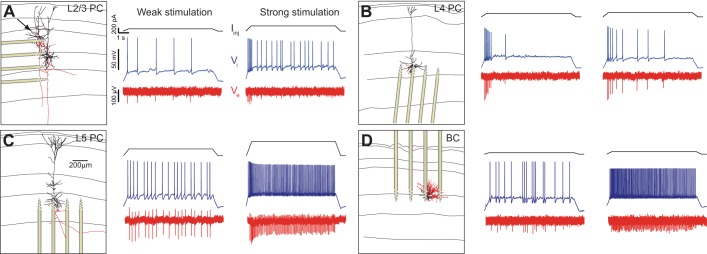
Intracellular somatic spiking and its extracellular reflection as measured by the 32-site silicon probe recordings in rat somatosensory slices from a L23 pyramidal neuron (L23PC; A), L4 pyramidal neuron (L4PC; B), L5 pyramidal neuron (L5PC; C), and L3 basket cell (L3BC; D). Left: images of the reconstructed neural morphology (dendrites: black; axon: red; horizontal lines indicate cortical layers) and location of silicon probe from individual experiments. (The arrow in A shows the patched L23 neuron.) Somatic spiking is induced via administration of a suprathreshold 9-s DC intracellular step of variable strength. Administration of small amplitude DC current (weak stimulation) resulted in slow spiking (middle) while an increase in the amplitude (strong stimulation) gives rise to faster spiking (right). Intracellular current stimulus is shown on top (black), intracellular somatic voltage response (blue) in the middle, extracellular voltage (as recorded from electrode of the silicon probe closest to the soma; red) at the bottom.

Spatial scaling of EAPs.

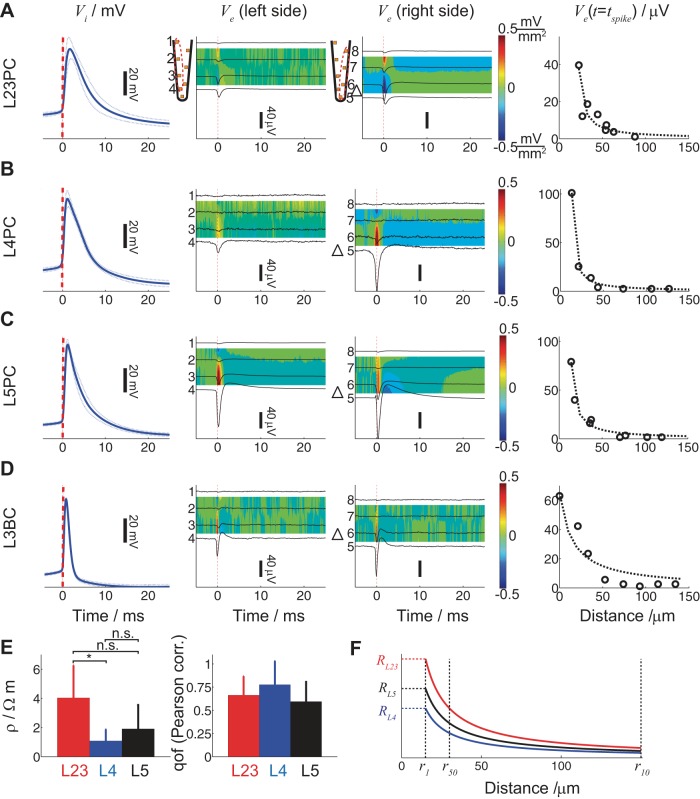
What are the physical properties of extracellular space and how are intracellular and transmembrane signals reflected and propagated in it? We calculated the STA from spikes as measured intracellularly by aligning the intracellular action potential waveform at the time of spike t_spike defined as the maximum of the second-order temporal derivative of V_i before the characteristic positivity (Fig. 2, A–D, 1st column; solid blue line: mean intracellular STA; dashed blue lines: SD; dashed red line: spike time). We show the results from four individual neurons, a L23 (Fig. 2A), a L4 (Fig. 2B), and a L5 (Fig. 2C) pyramidal neuron as well as a L3 (Fig. 2D) basket cell. Using the intracellular spike times, we temporally aligned the EAP waveforms recorded along the shank closest to the patch-clamped soma for the four electrodes along the left and right side of this one shank, respectively, for the four neurons (Fig. 2, A–D, left shank side: 2nd column; right shank side: 3rd column; black lines: mean V_e). The current source density (CSD), approximated by the negative second spatial derivative of V_e along the shank (Nicholson 1973), is plotted in color (location of the cell body along the depth axis is indicated by a triangle). The CSD represents the volume density of the net current entering or leaving the extracellular space and has been typically used to determine spatiotemporal patterns of synaptic activity (Buzsáki et al. 2012). Our measurements show the EAP and CSD contribution of spiking currents of individual neurons.

Fig. 2.

Intra- and extracellular action potentials (APs) for the cells shown in Fig. 1 as recorded from the whole cell patch electrode as well as by 8 electrodes along the shank located most proximal to the spiking neuron. A–D: spike-triggered intra- and extracellular responses for a L23 (A), L4 (B), and L5 (C) pyramidal neuron as well as a L3 (D) basket cell. 1st Column: spike-triggered average of V_i aligned at t_spike determined as the maximum of the second time derivative of V_i right before the maximum V_i (blue line: mean; broken line: SD). All spike-triggered average V_i traces are aligned at t_spike (dashed red line). 2nd and 3rd Columns: spike-triggered average of the recorded V_e (black lines) from the left (2nd column) and right 4 electrodes (3rd column) of the most proximal shank adjacent to the soma (schematized by the triangle). Colors indicate the mean spike-triggered current source density (red: source; blue: sink) attributed to spiking. 4th Column: extracellular action potential (EAP) amplitude at t_spike as a function of distance between the whole cell-patched soma and extracellular sites along the shank closest to the soma. E: extracellular resistivity ρ (left) and quality of fit (right; 0 no correlation and 1 perfect fit) for 9 L2/3 (red), 4 L4 (blue), and 12 L5 (black) pyramidal neurons for the extracellular voltage inferred by assuming a current point source in a purely resistive cytoplasm (see text). Comparison between layer-specific ρ yielded statistically significant difference between ρ_L23PC and ρ_L4PC (ANOVA, P < 0.05); qof, quality of fit. F: based on the layer-specific ρ (same color coding as in E), the ratio R = V_e/I = ρ/4πr is calculated as a function of distance with distances r₅₀ and r₁₀ designating the distance where the EAP amplitude becomes 50 and 10%, respectively, compared with the EAP amplitude 10 μm (r₁) from the cell body.

A frequently made assumption is that the extracellular milieu is described by a purely homogeneous and isotropic ohmic conductivity (Ranck 1963; Logothetis et al. 2007; Anastassiou et al. 2011 but see also Gabriel et al. 1996; Bédard et al. 2004), with V_e governed by Laplace's equation ∇²V_e = 0. The boundary condition along a cable-like source is given by (1/ρ)∇V_e·n = J with J being the transmembrane current density and ρ the extracellular resistivity (Holt 1998). In the special case for a single point source in an unbounded isotropic volume conductor, the solution becomes V_e = Iρ/4πr, in which I (unit, A) is the current amplitude of the point source and r (unit, m) is the distance from the current source to the measurement site, i.e., the spatial scaling of V_e is inversely proportional to the distance from the current source I. We tested the conductivity characteristics of the extracellular milieu at length scales relevant to neurons (i.e., tens of μm) and realistic current sinks and sources (i.e., membrane currents of identified neurons during spiking) by plotting the mean EAP amplitude measured from the eight electrodes along the closest shank at t_spike as a function of distance from the cell body (see materials and methods). As expected, EAP amplitude decreases for increasing distance (Fig. 2, A–D, 4th column; circles: mean EAP amplitude).

As observed, at t_spike, EAP amplitude decays as a monopole (Fig. 2, 4th column; broken line: least squares fit of 1/r function). To quantify ρ, we fit V_e(t_spike) = I(t_spike)ρ/4πr where I(t_spike) = −CdV_i(t_spike)/dt with C (unit, F) being the cell capacitance and V_i (unit, V) the intracellular somatic voltage as measured by the patching pipette. The cell capacitance C and resistance R were measured for each cell by injecting an intracellular subthreshold current and fitting the membrane response to an RC response. It has been shown that −CdV_i(t_spike)/dt satisfactorily approximates spike-related currents I(t_spike) (Harris et al. 2000) and we found this to hold for the first 0.5–1 ms after t_spike (data not shown). Based on the aforementioned, we determined the extracellular resistivity ρ (unit, Ωm) for 9 L23 pyramidal neurons (red), 4 L4 pyramidal neurons (blue), and 12 L5 pyramidal neurons (black) and found it to be ρ_L23PC = 2.9 ± 2.5 Ωm, ρ_L4PC = 1.4 ± 1.1 Ωm, and ρ_L5PC = 2.3 ± 4.2 Ωm (Fig. 2E, left; means ± SD). (The main reason for the large SD is the problematic estimation of C rather than poor EAP distance scaling.) A statistically significant difference in resistivity was measured between ρ_L23PC and ρ_L4PC (ANOVA, P < 0.05) with the rest of comparisons being statistically insignificant.

We also report the Pearson correlation as a measure for the quality of fit (0: no correlation; 1: perfect fit; mean ± SD) of the spatial scaling of the EAP amplitude to the point-source approximation. As observed, there is good agreement between the measured spatial scaling of EAP amplitude and point-source approximation (Fig. 2E, right). Based on the point-source approximation, ratio R = V_e/I = ρ/4πr can be calculated as well as distances r₅₀ and r₁₀ from the soma where the EAP amplitude is reduced to half and a tenth, respectively, the EAP amplitude at 10 μm (r₁) away from the cell body (Fig. 2F). (Notably, this depiction assumes identical current source I for all cell types.)

Temporal features of EAPs.

So far, our analysis relied on extracellular signals measured at one instant, t_spike. Yet, the EAP waveform does not only have spatial features, it also has temporal ones. What are the temporal EAP characteristics and, importantly, what is their variation? For example, while the most salient feature of the intracellular (extracellular) spike waveform is the transient, ∼0.5- to 1 ms-long, Na- and K-dependent positivity (negativity), analyzing the recorded waveforms reveals that spectral content of spikes is significantly stronger at lower frequencies than in the 500- to 2,000-Hz range of the spectrum. Furthermore, pyramidal neurons have consistently slower action potential and EAP waveforms than basket cell interneurons (Fig. 3A; blue: mean V_i; red: strongest EAP signals from the left and right part of the shank closest to the soma), an observation in agreement with previous studies (Pettersen and Einevoll 2008; Schomburg et al. 2012, although see also Vigneswaran et al. 2011).

To study temporal EAP features, we focus on the EAP signature as recorded along each side of the shank nearest to the patched neuron. Specifically, we normalize the EAP amplitude across sites and study the time differences in EAP minima along each shank side (Fig. 3B; black line designates EAP minimum for recorded signals). We have two definitions of time delay: the first uses t_spike as measured intracellularly as time reference (Fig. 3C, black) while the second uses the time t_EAP of the minimum of the largest EAP deflection (Fig. 3C, cyan). The temporal delay between EAPs along the shank is typically smaller than 0.4–0.5 ms. Since the location and interelectrode distances along a shank are known, we can calculate the velocity v of the EAP signal propagation by dividing the interelectrode distance Δx by the (absolute) time delay Δt of EAP negativities, v = Δx/Δt (Fig. 3D). Once more, we have two definitions of velocity: the first takes Δt to be the time difference between EAP negativities across successive electrodes (Fig. 3D, black) while the second takes Δt to be the time difference between the EAP negativity of each electrode and the one of the strongest EAP (Fig. 3D, cyan). Both velocity definitions result in similar outcomes, i.e., the EAP signal propagation velocity of spikes along the shank for all cells is ∼0.5–2 mm/ms.

How do such temporal EAP delays and propagation arise? One hypothesis is that the extracellular medium has both a resistive and a capacitive component with the latter giving rise to temporal delays in the propagation of the EAP signal from the soma to the extracellular site (Ranck 1963; Gabriel et al. 1996; Bédard et al. 2004; Bédard and Destexhe 2009). Given the measured extracellular resistivity, the extracellular medium would need to have a capacitance of ∼1,012 F/m to give rise to the time delays typically observed along a shank, which is orders of magnitude greater than estimates of extracellular capacitance (see discussion for details) (Koch 1999). Furthermore, such large capacitances would show up in a loss of high-frequency components in the EAP, which is not the case as seen in Fig. 3A. While we cannot exclude the possibility of some extracellular capacitive components, at least for spiking, our experiments suggest that such effects are small.

An alternative hypothesis is that action potentials elicited at the axon initial segment propagate back into the dendrites (Stuart et al. 1997; Shai et al. 2014, 2015; Koch 1999). In this case, extracellular sites closer to dendrites than the soma (especially sites closer to the thick main apical dendrite; Henze and Buzsáki 2001) record backpropagating action potentials rather than directly somatic ones. A first indication in support of this hypothesis is that the time delay definition with reference to the minimum of the strongest downward EAP deflection (Fig. 3C, cyan) is in the vast majority positive, suggesting the site closest to the cell body precedes the EAP deflection in other sites. Moreover, the same delay definition gives rise to fairly monotonic trends, which, given the sites of the shank typically closest to the cell body, are the ones on the edge (sites 4 and 5 in Fig. 2, B–D). This points to the traveling nature of the signal. An additional indication is that the point-source approximation quantitatively fits the EAP amplitude vs. distance relationship only for the spike initiation time. When the same relationship is plotted for the overall EAP amplitude, i.e., the EAP amplitude for all times (and not specifically the spike initiation time) along the shank, the quality of fit of the point-source approximation attenuates, suggesting EAP delays are predominantly attributed to spike backpropagation.

To further assess this hypothesis, we performed simulations using a biophysically and anatomically faithful model of rat somatosensory L5 pyramidal neurons that supports backpropagating action potentials (Hay et al. 2011) (see materials and methods). As in our experimental setup, we inject current steps into the somatic compartment of the model (Fig. 3E; blue: V_i response to current injection) and calculate V_e under the assumption of a purely resistive medium (Holt and Koch 1999; Gold et al. 2006; Pettersen and Einevoll 2008; Reimann et al. 2013, ρ = 2.5 Ωm) at locations very similar to the position of the silicon probe shank in an experiment with the L5 pyramidal neuron shown in Fig. 1C (Fig. 3E, middle red trace). In another approach, we compute V_e by only considering the contribution of the somatic compartments (Fig. 3E, bottom red trace). Following Fig. 3B, we calculate the mean EAP waveform for the eight recordings based on the intracellular spike time t_spike, four for each side of the shank, and normalize the EAP amplitude (Fig. 3F; red: mean; black line designates EAP minimum for all recorded signals). While for the EAP signal contributed from the whole neural morphology, time delays in the EAP minimum appear, this is not the case for the EAP signal contributed from the soma only. Moreover, the time delays observed in the simulation are very similar to the ones measured in our experiments (compare Fig. 3B, case L5PC with Fig. 3F, top).

Changes in the EAP waveform as a function of firing rate and spiking order.

Beyond temporal delays of EAP negativities along a single shank, extracellular spike waveforms show considerable variability even when recordings are performed from a single spiking cell and the same extracellular recording site (Hill et al. 2011), with such variability particularly enhanced during bursting, i.e., high-frequency (>200 Hz) spiking, of cortical neurons (Buzsáki et al. 1996; Henze et al. 2000; Harris et al. 2003). Yet, bursts are comparatively rare events. What is the inherent variability of the EAP waveform as a function of neural activity? This question has been difficult to address in vivo given there is no obvious way of discriminating “natural” EAP variability from other occurrences such as electrode displacement, motion artifacts and coupling to electric fields associated with muscular activity (Schomburg et al. 2014).

We investigated the extent to which the EAP waveform changes as a function of spike rate. That is, we ascribed an interspike interval (ISI) to every spike (ISI definition: time difference between the previous and the current spike) with spike times determined from the intracellular somatic recording. Stimulation of the whole cell patched neurons with DC intracellular stimuli of varying strength resulted in Gaussian-like spike frequency histograms with spike frequency defined as 1/ISI (Fig. 4A; blue: intracellular voltage; red: extracellular trace from the closest electrode to the soma; black: ISI histogram of a L5 pyramidal neuron).

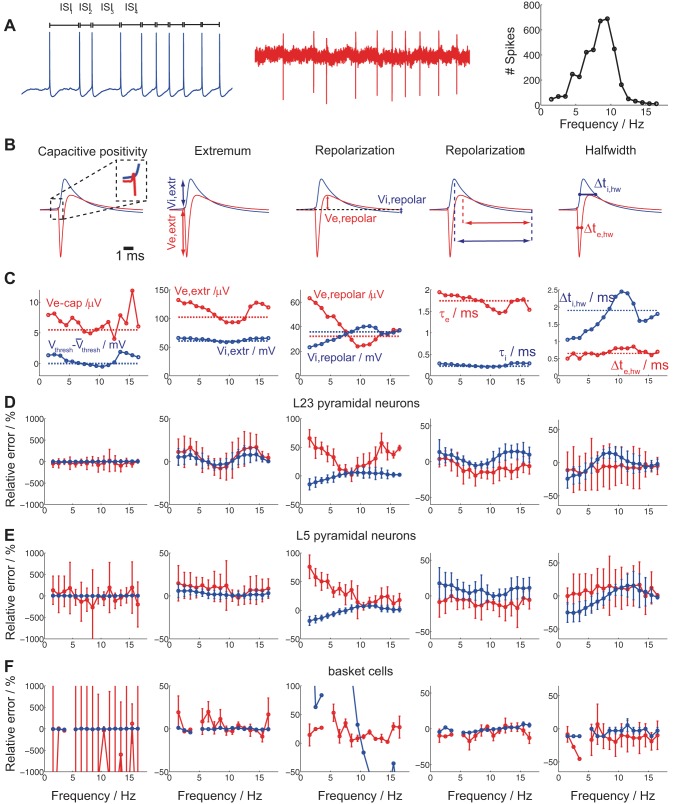
Fig. 4.

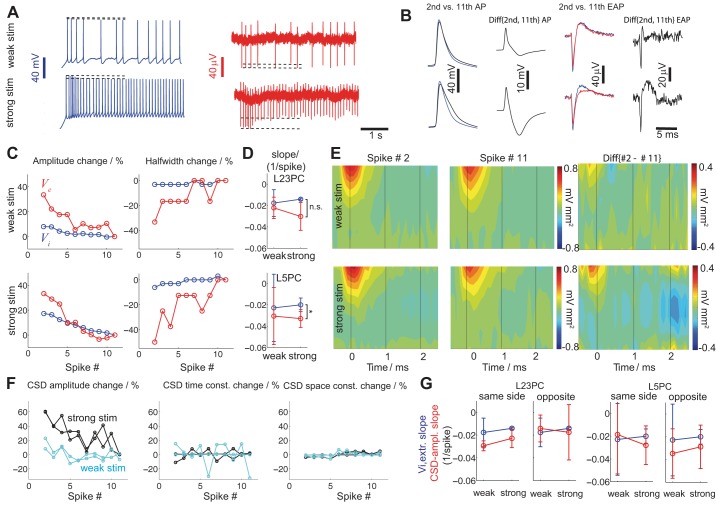
Cell type-specific intra- and extracellular spike-waveform characteristics as a function of spike frequency. A: intracellular somatic DC current injection of varying strength results in intracellularly (blue) and extracellularly (red) recorded spikes. Spike frequency is defined for each spike as the inverse of its ISI resulting in a Gaussian-like spike frequency histogram (right). B: 5 extracellular spike-waveform characteristics were studied (left to right): the initial capacitive positivity (V_e,cap) amplitude, the EAP negativity amplitude (V_e,extr), the EAP repolarization positive (V_e,repol) amplitude, the EAP repolarization time τ_e, and the EAP half-width Δt_e,hw (features designated in red). Likewise, 5 intracellular spike waveform characteristics were analyzed (left to right): change in voltage spike threshold compared with the mean, the intracellular spike-amplitude (V_i,extr), the intracellular postspike negativity (V_i,repol) amplitude (compared to baseline), the intracellular spike repolarization time τ_i, and the intracellular spike half-width Δt_i,hw (features designated in blue). C: intra- (solid blue)- and extracellular (solid red) spike-waveform characteristics as a function of spike frequency for the L5 pyramidal neuron in A. Broken lines indicate the mean of each intra- and extracellular spike-feature across spike frequencies. D–F: differences in intra- and extracellular spike waveform characteristics (C) as a function of spike frequency with reference to the mean waveform across all spikes irrespective of spike frequency for 8 L23 (D) and 12 L5 (E) pyramidal neuron recordings as well as 4 basket cell (F) recordings (red: extracellullar feature; blue: intracellular features; circles: mean; error bars: SD). Differences are expressed as the relative error (for more thorough explanation, see text). V_e,extr variability is consistently larger than V_i,extr variability for all cell types (2nd and 3rd columns; basket cell variability in the 3rd column, in blue, is attributed to repolarization being very close to baseline) while temporal feature variability much less so (4th and 5th column).

We assessed both intracellular and extracellular spike waveforms from the same cell for different spike frequencies. We focus on five EAP characteristics: 1) the initial capacitive positivity (V_e,cap) amplitude; 2) the EAP negativity amplitude (V_e,extr); 3) the EAP repolarization positivity (V_e,repol) amplitude; 4) the EAP repolarization time τ_e; and 5) the EAP half-width Δτ_e,hw at half height (Fig. 4B; all features designated in red). Concurrently, we report the correlates of intracellular spike waveforms of the aforementioned features: 1) the change in intracellular voltage spike threshold compared with the mean; 2) the intracellular spike amplitude (V_i,extr); 3) the intracellular postspike negativity (V_i,repol) amplitude (compared to baseline); 4) the intracellular spike repolarization time τ_i; and 5) the intracellular spike half-width Δτ_i,hw (Fig. 4B; all features designated in blue). In Fig. 4C we show how these spike-waveform characteristics change with spike frequency for a single L5 pyramidal neuron (spike frequency histogram shown in Fig. 4A). Note how EAP amplitude characteristics (in red) vary more with spike frequency than their intracellular correlates (in blue). For example, while V_e,extr = 102 ± 14 μV (mean ± SD), V_i,extr = 61 ± 3 mV with the COV (defined as the ratio between the SD and mean) being 0.14 vs. 0.05, i.e., almost three times larger for V_e,extr than for V_i,extr. On the other hand, variability in extracellular temporal characteristics is broadly similar to their intracellular correlates. For example, for Δτ_e,hw and Δτ_i,hw the COV is 0.16 vs. 0.24, revealing larger variability in the temporal characteristics of intracellular than extracellular spikes. Interestingly, it was recently shown that intrinsic biophysical mechanisms are activated along the dendrites of CA1 pyramidal neurons in theta and gamma bandwidths (Vaida and Johnston 2013). In our experiments we observed consistent changes in EAP features (most visible in V_e,extr and V_e,repol) in the theta-frequency bandwidth (4–12 Hz).

In Fig. 4, D–F, we report how spike waveform characteristics change as a function of spike frequency with reference to the mean waveform across all spikes from an individual neuron, irrespective of spike frequency for 8 L23 (D) and 12 L5 (E) pyramidal neuron recordings as well as 4 basket cell (F) recordings. We report the relative error for each feature. For example, for the EAP amplitude, we report ratio V_e,extr − < V_e,extr >/< V_e,ampl > with V_e,extr being the EAP amplitude in a particular spike frequency bin and < V_e,ampl > the mean EAP amplitude across all spikes. We express the ratio in form of percentual change (line: mean; error bar: SD; red: extracellular feature; blue: intracellular feature). As observed, there is substantial variation in the two most salient EAP features, the EAP amplitude V_e,extr (Fig. 4, D–F, 2nd column) and the EAP repolarization amplitude V_e,repol (Fig. 4, D–F, 3rd column) for all cell types. Importantly, the relative error in these features is consistently larger in the extracellular rather than the intracellular waveforms (compare red to blue) and nonmonotonic as a function of spike frequency. On the other hand, the relative error in repolarization time shows larger variability in intracellular than extracellular spike waveforms while being similar for the halfwidth time. We did not find any distinguishing differences in relative error between cell types.

Transient membrane conductances such as sodium inactivation and slower calcium-dependent currents can alter spike shape (Buzsáki et al. 1996; Henze et al. 2000). In Fig. 5A, intracellular stimulation of varying strength (top: weak; bottom: strong) yields spike trains of ∼3 (top) and 10 Hz (bottom) for a L5 pyramidal neuron. While for weak stimuli there is little variation in intra- and extracellular spike waveforms (dashed lines: amplitude-range), for strong stimulation the amplitude of the spike waveform (especially the extracellular) changes substantially between the first and subsequent spikes despite their similar ISIs. To quantify such intra- and extracellular spike waveform variability, we repeated the same somatic injection multiple times, calculated the mean waveforms of the first, second, third, etc. spike, and subtracted them. Using this procedure, we calculate the mean difference between intra- and extracellular spike waveforms as a function of spike occurrence for weak and strong stimulation (Fig. 5B). In Fig. 5C we report the change (relative error) in (left) intra (V_i,extr, blue) vs. extracellular amplitude (V_e,extr, red) and (right) halfwidth (Δτ_i,hw vs. Δτ_e,hw) as a function of spike order comparing the first 10 spikes to the 11th for weak (top) and strong (bottom) stimulation. For example, to calculate the relative error in V_e,extr amplitude for a particular stimulation strength, we calculate (V_e,extr − V_e,extr^11th/V_e,extr^11th) with V_e,extr being the EAP negativity (as defined per Fig. 4) for each of the spike order bins and V_e,extr^11th being the EAP negativity of the 11th spike bin. It is observed that for increasing spike order, EAP amplitude decreases and EAP width increases, that is, EAPs becomes smaller and wider. Moreover, compared with the intracellular waveform, the decrease in amplitude and increase in width are much enhanced. In Fig. 5D, we assess this observation for the spike amplitude by fitting the data shown in Fig. 5C, left, with a linear function (least-squares fit with y = ax + b where a is the slope and b the offset) and report the normalized slope a/b for L23 (top) and L5 (bottom) pyramids for intra (blue)- and extracellular (red) spike waveforms as a function of stimulus amplitude. For both cell types the rate of amplitude change is negative, i.e., intra- and extracellular spike amplitude decreases as a function of spike order. Moreover, for L23 pyramids, for weak and strong stimulation, the rate of decrease (slope) does not differ significantly between intra- and extracellular spikes. This is not the case for L5 pyramids where for strong stimulation, the intra- and extracellular spike amplitude decrease is significantly (ANOVA, P < 0.05) different, suggesting that the decrease in EAP amplitude does not proportionally reflect the intracellular one. Such observations are partly attributed to the fact that EAPs reflect both somatic and dendritic, i.e., distributed and inhomogeneous, electrogenesis (Koch 1999).

Fig. 5.

Spike waveform variability with stimulation intensity and spike order. A: for weak intracellular DC stimulation of a L5 pyramidal neuron (top) the features of the intracellular (blue) and extracellular (red) traces remain largely invariant (broken lines designate AP and EAP amplitude of spikes at the beginning and 2.5 s from stimulus onset). For strong stimulation (bottom), intracellular and extracellular traces contain spikes whose amplitude changes with spike order (broken lines; compare with top). B: comparison between 2nd (blue) and 11th intracellular spike (black) aligned at t_spike (left) reveals small differences for weak (top) stimulation that become more pronounced for strong stimulation (bottom). 2nd Column: difference between the 2nd and 11th intracellular AP waveform (mean of 5 experiments with identical input; blue minus black in leftmost panels). 3rd And 4th columns: same for EAP waveforms. C: intra- and extracellular features as function of spike order [left: V_i,extr (blue) vs. V_e,extr change (red); right: Δt_i,hw vs. Δt_e,hw change] for weak (top) and strong (bottom) stimulation (same L5 pyramidal neuron as in A and B). Relative error compared with the last (11th) spike considered (relative error for all features for the 11th spikes equal zero). D: slope of the amplitude change (as reported in C; see also text) for the intra (blue)- and extracellular (red) EAPs for L23 (top) and L5 pyramidal neurons (bottom) as a function of stimulation amplitude (circles: mean; error bars: SE). Statistical testing (ANOVA, P < 0.05) reveals significant difference between the amplitude gradient of intra- and extracellular L5 pyramids. E: mean current source density (CSD) (left shank) of the 2nd and 11th spike for a L5 pyramidal neuron (same as in A–C) for weak (top) and strong (bottom) stimulation (left and middle). The difference in mean CSD between the 2nd and 11th spike is shown in the right. F: relative error in amplitude, time, and spatial features of the CSD as a function of spike order for a L5 pyramidal neuron as expressed by (left to right) CSD amplitude (A_CSD)/Ā_CSD − 1, σ_t/σ̄_t − 1 and σ_x/σ̄_x − 1 with Ā_CSD, σ̄_t, and σ̄_x being the mean CSD amplitude, time, and space constant, respectively (cyan: weak stimulation; black: strong stimulation; 2 lines: CSD changes along 2 sides of the same shank). G: slope of the linear fit to the mean A_CSD as a function of spike order normalized by the A_CSD for each cell (blue: intracellular; red: extracellular; circles: mean; error bars: SD) for L23 (left) and L5 (right) pyramidal neurons for the 4 shank electrodes on the same vs. the opposite side of the soma. Statistical testing (ANOVA, P < 0.05) revealed no significant difference between intracellular and A_CSD slopes. Furthermore, no statistically significant difference was found for A_CSD slopes between weak and strong stimulation.

What is the spatial dependence of these observations? In Fig. 5E (left and middle) we show the mean CSD of the 2nd vs. 11th spike for weak (top) and strong (bottom) stimulation (same L5 pyramid as in Fig. 5, A and B; see right in Fig. 5B for EAP differences) and show their difference in Fig. 5E, right. By subtracting CSDs of the same neuron for different spike occurrences it becomes evident that, for the particular L5 pyramid, strong stimulation and fast spiking results in a different spatiotemporal CSD constellation compared with weak stimulation and slow spiking. To quantify these differences, we fit a two-dimensional Gaussian function G(x,t) = A_CSD exp $\left(-\frac{{\left(t-t_0\right)}^2}{2{\sigma }_t^2}-\frac{{\left(x-x_0\right)}^2}{2{\sigma }_x^2}\right)$ 1 ms around t_spike (Fig. 5E, time = 0) and plot the relative error (Fig. 5F, left to right) in CSD amplitude (A_CSD), space (σ_x), and time (σ_t) constant as a function of spike occurrence with reference to the 11th spike (Fig. 5F, black: strong stimulation; cyan: weak stimulation; same colored lines: results for both sides of the shank closest to soma; data from same cell as in Fig. 5A-C). While changes in spatial and temporal constant broadly existed, the most sensitive parameter to the spike order for weak vs. strong stimulation is the CSD amplitude that, in the case of strong stimulation, changed by ∼60% for that neuron. To assess this effect quantitatively, we follow the method introduced in Fig. 5, C and D, and fit the CSD amplitude vs. spike order data with a linear function for a set of L23 and L5 pyramidal neurons and report the normalized slope (Fig. 5G). We do so for the CSD amplitude change (red) as a function of cell type (L23 vs. L5 pyramids), shank side (CSD calculated from the 4 electrodes on the same vs. the opposite side the cell body), stimulation amplitude (weak vs. strong) and compare it with the V_i,extr change (blue; same data as in D). The negative value of the slopes illustrates that also CSD amplitude decreases with spike order. Yet, unlike in Fig. 5D, the comparison between V_i,extr-amplitude slope and CSD-amplitude slope is statistically insignificant, suggesting that (unlike for V_e,extr of L5 pyramids shown in Fig. 5D) CSD-amplitude decrease reflects the measured V_i,extr decrease. These observations remain broadly similar for L23 and L4 pyramids.

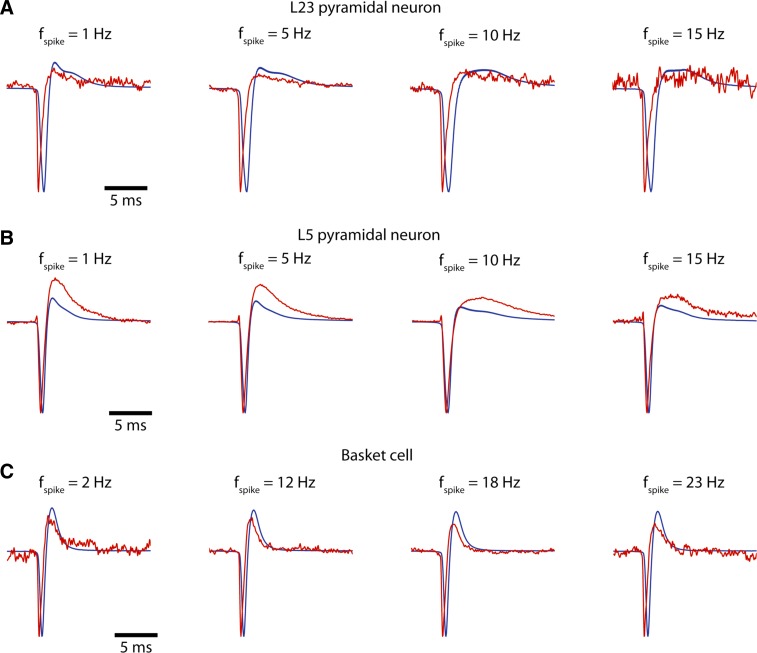
Figures 4 and 5 suggest that the relationship between the EAP waveform and V_i is complicated. In fact, biophysical considerations support that the negative derivative of the intracellular potential is proportional to the EAP waveform (Koch 1999). To assess this, in Fig. 6 we plotted the amplitude normalized −dV_i/dt and the EAP waveform for (A–C) a L23 and a L4 pyramid as well as for a basket cell (same cells as in Fig. 2). We show this relationship for increasing (left to right) spike rates (with the spike rate assessed the same as in Fig. 4). Indeed, the two waveforms are qualitatively similar in shape (importantly, not in absolute amplitude) during the initial Na and K component of the spike. The comparison becomes poorer after the EAP negativity when slower, repolarizing currents are activated that cannot be captured by simply differentiating V_i. Concurrently, during such later stages of spike initiation, charge transfer is no more confined perisomatically but has propagated along the morphology casting the entire neuron a spatially distributed sink/source contributing to the extracellular potential.

Fig. 6.

Comparison between EAP waveform with the negative 1st-order time-derivative of the intracellular AP waveform, −dV_i/dt, for different cell types (A–C: a L23 pyramid, a L5 pyramid, and a basket cell). Intracellular stimuli of varying strength are applied (see Fig. 1) resulting in spikes of varying interspike interval (ISI). Spike frequency is then defined as 1/ISI and spikes are grouped. The figure shows the mean extracellular (red) and the mean −dV_i/dt (blue) for difference spike frequencies. (Waveforms are scaled so as to have the same amplitude.) As observed, the EAP and −dV_i/dt waveforms are in close agreement (width, etc.) near the EAP negativity. Comparison between the EAP and −dV_i/dt waveform becomes poorer ∼1 ms after the EAP negativity when slower, repolarizing currents are activated.

Low-frequency contributions of EAPs.

Recent computational (Denker et al. 2011; Schomburg et al. 2012; Reimann et al. 2013) and experimental in vivo (Ray and Maunsell 2011; Belluscio et al. 2012) studies support the notion that extracellular spike waveforms not only contribute to the higher frequency portion of V_e recordings but also impact lower bandwidths. Addressing and quantifying such effects has proven difficult, especially since capturing the slower, mostly repolarizing, spike currents of smaller amplitude is challenging.

We used the STA EAP waveforms from identified cells (Fig. 7A, red) to construct fictitious extracellular traces and analyze their power with and without spikes. Nine-second-long V_e recordings from an extracellular site far from the patched neuron that did not detect any spiking (as assessed from the STA) was the baseline. To this, EAP waveforms at ISIs drawn from a log-normal distribution (Mizuseki and Buzsáki 2013; Buzsáki and Mizuseki 2014) with mean spike frequency f₀ were added at three spike rates, f₀ = 1, 8, and 30 Hz (Fig. 7B). In a next step, we calculated 50 realizations for each f₀, which resulted in 50 unique (Fig. 7, C–E) 9-s-long extracellular traces. We then calculated their spectral content (Fig. 7F; line: mean spectral power from 50 traces using the EAP of a L5 pyramidal neuron shown in Fig. 7A1; green: no spiking; red: f₀ = 1-Hz spiking; black: f₀ = 8 Hz; blue: f₀ = 30 Hz). As observed, there is substantial deviation in spectral power between the spiking and no- or low-spiking traces at frequencies as low as 20 Hz.

What part of the EAP waveform can impact power at such low frequencies? To address this question, we performed so-called “de-spiking,” i.e., we substituted a window of 0.6 ms before and after the spike initiation time t_spike with a spline fit (Belluscio et al. 2012). This resulted in EAP waveforms lacking the typical spike negativity but containing the repolarization (Fig. 7A; de-spiked EAP waveform in black). We calculated the spectral power for the same f₀ using the de-spiked waveforms (Fig. 7G) and confirmed our previous conclusion: reasonably high spiking impacts spectral power as low as 20 Hz compared with no or low spiking. Moreover, we attribute the difference in frequency scaling between intact and de-spiked waveforms beyond 50 Hz to the impact of the EAP negativity (compare Fig. 7, F and G). Importantly, when the same analyses using the EAP waveform from basket cells was performed (Fig. 7, A3 and A4), the outcome is very different: spiking minimally contributes to spectral power under ∼100 Hz and, even then, does so only for elevated spike frequencies (Fig. 7H). We attribute the lack of impact of basket cell spiking to local field potentials (LFPs) <100 Hz to their temporally narrow EAP waveform as well as the lack of long-lasting depolarizing currents (compare intracellular waveforms between Fig. 2, A–C, and D). The conclusions for Fig. 7, F–H, are supported by statistical tests (t-testing) we performed (Figs. 7, I–K) where spectral power between no spiking (control) and spiking cases (red: comparison between control and 1-Hz spiking; black: comparison between control and 8-Hz spiking; blue: comparison between control and 30-Hz spiking) was pairwise compared at various frequencies (steps of 5 Hz; null hypothesis: spectral power between spiking traces and controls are drawn from the same distribution; dashed lines: P = 10⁻³, Bonferroni corrected for multiple comparisons). As observed, for EAPs from a L5 pyramidal neuron, spiking significantly impacts spectral power of the extracellular recording as low as 20 Hz for f₀ greater than 1 Hz (Fig. 7I), an observation mainly attributed to repolarization currents as the difference remains when EAP negativities have been removed (Fig. 7J).

Of course, extracellular electrodes usually pick up EAPs from multiple neurons. Indeed, they typically record larger amplitude EAPs (larger than 50-μV amplitude) from only a few individual neurons located very closely and smaller-amplitude EAPs from many more located in the greater vicinity (Buzsáki 2004; Holt and Koch 1999; Gold et al. 2006; Schomburg et al. 2012) (see also Fig. 2). To account for this, in Fig. 7, L–N, we performed the same analyses as in Fig. 7, I and J, but instead of using the EAP waveform from a single neuron we used EAP waveforms from multiple cells. To do so, we define the overall spike frequency f_MUA attributed to spiking from all cells (equivalent to multiunit activity or MUA) and at each ISI (drawn from a log-normal distribution; Fig. 7, C–E) we sum the EAP waveform of a randomly chosen neuron (of the same cell type) from 8 L23 pyramidal neurons (Fig. 7, L–N, left), 4 L4 pyramidal neurons (Fig. 7, L–N, middle), and 12 L5 pyramidal neurons (Fig. 7, L–N, right) with a control trace (recorded from far away) for spike rate f_MUA = 8, 32, and 96 Hz (in each of Fig. 7, L–N, from left to right). The resulting V_e traces (similar to the ones shown in Fig. 7B) contain EAP waveforms from many neurons of a particular type. We show the statistical significance (t-test, dashed line: P < 10⁻³, Bonferroni corrected for multiple comparisons) of the difference in spectral power between control (no spiking) and spiking traces at different frequencies (steps of 5 Hz; null hypothesis: spectral power between control and spiking traces are drawn from the same distribution) for intact (red) and de-spiked (black) EAP waveforms. As observed, while for f_MUA = 8 Hz (equivalent to 8 neurons spiking at 1 Hz) spiking does not substantially impact spectral power below 100 Hz, for faster (but still very realistic) rates of f_MUA = 32 and 96 Hz, spiking profoundly impacts spectral power at frequencies as low as 20 Hz. This is especially true for L4 and L5 pyramidal neurons. We also studied the effect of different EAP waveforms as measured by different sites along the shank by considering the strongest and second and third strongest EAP signals, both for the intact and de-spiked EAP waveforms (Fig. 7, L–N, 3 lines of the same color). While the strongest EAP waveforms (cell type: mean EAP amplitude ± SD; L23PC: 39 ± 10 μV; L4PC: 57 ± 35 μV; L5PC: 51 ± 61 μV) impact spectral density at low frequencies already for f_MUA = 32 Hz, broadly the same effects hold even when considering the second strongest EAP waveforms of the same neurons (cell type: mean EAP amplitude ± SD; L23PC: 32 ± 7 μV; L4PC: 30 ± 4 μV; L5PC: 40 ± 10 μV).

DISCUSSION

Assessing the neural origins of electric signals has remained problematic even if the biophysical laws governing the initiation and propagation of these electric events are well understood (Mitzdorf 1985; Logothetis and Wandell 2004; Buzsáki et al. 2012; Einevoll et al. 2013). Our experimental setup allows us to access intracellularly and whole cell patch-clamp somata of identified neurons located a few tens of micrometers away from extracellular silicon probes of known spatial constellation. By stimulating these identified neurons through intracellular DC current injections and eliciting spikes, we recorded intracellular and extracellular spiking signals. Notably, access to the intracellular voltage allows precise detection of spike times, alignment of intracellular and extracellular voltage traces, and reliable intracellular and extracellular STA. The latter is essential to our study as it allows experiment (distance to extracellular recording sites)- and cell type-specific (extracellular resistivity, slow vs. fast spiking) comparisons while doing away with the ambiguity of thresholding and origin (single vs. multiple neurons) of these signals. Using these experiments we addressed three questions: the spatial EAP propagation in cortical matter, temporal effects of EAPs, and spike contribution to the LFP.

Spatial EAP propagation.

To assess the physical properties of the extracellular medium such as the extracellular resistivity and characterize the EAP spread, we used a phenomenological model treating electrogenesis along the entire morphology at t_spike as a point source. While this way a number of processes and features are lumped into a single parameter/point, such an approximation offers many advantages over alternative experiments using microwires or parallel plates (Ranck 1963; Gabriel et al. 1996; Logothetis et al. 2007; Anastassiou et al. 2011) that lack spike-related electrogenesis. The use of the silicon probe allowed us to quantify the spatial spread of EAP signals at the microscopic level. We found that, at spike initiation time, the point-source approximation in a resistive medium (Holt and Koch 1999) captures the spatial decay of the EAP amplitude. Furthermore, by assuming current generation as the negative product of a cell's capacitance and the intracellular somatic derivative (Koch 1999), we calculated the microscopic, layer-specific extracellular resistivity and found it to be in agreement to studies quantifying it at the meso- and macroscopic level (Logothetis et al. 2007; Goto et al. 2010).

Temporal effects of EAPs.

We sought to understand variations in the extracellular spike negativity. We measured propagation delay and velocity along the silicon probe and found them to be in agreement with measurements of backpropagating action potentials (Stuart et al. 1997; Buzsáki et al. 1996; Buzsáki and Kandel 1998; Henze et al. 2000; Blanche et al. 2005). Thus we attribute such temporal variations to the contribution of dendritic compartments to the extracellular spike signal. This finding is seemingly in variance with the biophysical simulations of Gold et al. (2006), who suggested that it is mainly the cell body and proximal thick dendrites that affect the recorded EAP waveform. While true that the main contributor of the EAP waveform are perisomatic compartments of a neuron, more distal dendritic compartments also contribute to the recorded signal. In fact, our simulations suggest that only accounting for perisomatic compartments does not reproduce the observed time delays while strongly overestimating EAP amplitude close to the soma. Our findings are in line with computational (Pettersen and Einevoll 2008; Schomburg et al. 2012) and experimental (Buzsáki et al. 1996; Buzsáki and Kandel 1998; Henze et al. 2000; Blanche et al. 2005) work supporting the contribution of dendritic transmembrane currents to EAPs.

It has been hypothesized that temporal delays of EAPs can also appear if the extracellular medium has a capacitive component (in addition to its resistive nature) (Gabriel et al. 1996; Bédard et al. 2004; Bédard and Destexhe 2009). The main argument in favor of such a hypothesis is that the gray matter of cerebral cortex is filled with cellular membranes with the extracellular fluid taking up a fairly small volume (0.05–0.15) (Lopez-Aguado et al. 2001). Given the measured extracellular resistivity (∼2.5 Ωm) and the measured temporal delay (∼0.3 ms) observed in spike-negativity along a shank, assuming simple RC circuit formalism the extracellular medium would need to have a capacitance of ∼1,012 F/m. This is orders of magnitude larger than the membrane capacitance (Koch 1999). In fact, our data support that local, compartmental electrogenesis such as backpropagating action potentials through dendrites impacts EAP features such as amplitude and time delays rather than extracellular capacitance filtering. Yet, we cannot exclude that for larger distances and different/stronger current sources, there might be a capacitive feature (Bédard et al. 2004).

Yet, is the fact that the point-source approximation is a good fit for EAP distance scaling at t_spike not at odds with our observation that the whole cell morphology contributes to the EAP waveform? The short answer is no. Importantly, the point-source approximation (as presented in Fig. 2) is an apparent or phenomenological model of EAP distance scaling. Following the same argument, the extracellular resistivity as reported in Fig. 2 is a phenomenological property. By no means does such a model suggest that a single compartment contributes to the EAP nor should it encourage such a simplistic interpretation. Yet, it does give a first-order response to the question: given a certain distance between the cell body and the electrode, what is the EAP spread? Clearly, to address such a question in its entirety, a sophisticated three-dimensional model would be required that can fully simulate all electrogenesis (and its heterogeneity) in the intracellular, transmembrane, and extracellular space as well as in/around the recording electrode. As such, our phenomenological point-source model based on measured properties provides a useful first-order approximation, for example, for EAP spread (Fig. 2F).

An important aspect of extracellular recordings is their inherent, activity-dependent variability. Indeed, the EAP amplitude of hippocampal pyramidal neurons can vary as much as 60% during a high-frequency (>200 Hz) burst (Buzsáki et al. 1996), for example, within a place field (Harris et al. 2001). These features, together with artifactual sources of variability from electromyogram contamination or hardware sources, pose challenges for spike waveform-based clustering and classification of neurons in vivo. Our in vitro measurements present advantages over in vivo recordings, since variability of the EAP waveform is not affected by fluctuations of the membrane potential and spiking activity of other neurons. We chose spike frequency as an independent variable as in vivo measurements indicate that slow spiking gives rise to more stereotypical EAP waveforms than fast rates, e.g., during burst firing (Buzsáki et al. 1996; Harris et al. 2001). We report that the most salient features of EAPs, the EAP negativity attributed to fast sodium- and potassium-dependent currents and the immediately proceeding EAP positivity attributed to slower potassium (but also calcium) currents, can substantially vary as a function of spike frequency. In general, we found that spike variability of the EAP amplitude is more pronounced compared with intracellular spike variability (Henze et al. 2000), is nonmonotonic as a function of spike frequency, and is present in all cell types we studied. The temporal EAP features, such as halfwidth or decay time of spike repolarization, varied more reliably with the intracellular waveform than the amplitude (Barthó et al. 2004).

We also analyzed EAP features as a function of spike order (1st vs. 2nd vs. 3rd spike) and found that EAP amplitude of L5 pyramids decreased with spike order significantly more than the intracellular spike amplitude, an observation already established in vivo for CA1 pyramidal neurons (although for much higher spike rates) (Buzsáki et al. 1996). Such observations support the notion that perisomatic and, in fact, dendritic electrogenesis can vary and that a cascade of time-dependent and spatially distributed events is reflected in the EAP, much more so than in the intracellular somatic recordings of spikes (Gold et al. 2007; Anastassiou et al. 2013). Additionally, while EAP amplitude decrease cannot account for intracellular spike amplitude change (even if only for L5 pyramids), CSD amplitude decrease can, suggesting that single neuron CSDs or, alternatively, detection of spikes of individual neurons from multiple extracellular electrodes at known locations yields more robust spike measurements.

Finally, based on passive cable theory (Rall 1977), assuming an intracellular current injection I_inj at a specific location along a patch of membrane, the membrane current per unit length of cable, i_m(x,t), is given

$$i_{\text{m}}\left(x,t\right)=\frac{V_{\text{m}}\left(x,t\right)-V_{\text{rest}}}{r_{\text{m}}}+c_{\text{m}}\frac{\partial V_{\text{m}}\left(x,t\right)}{\partial t}-I_{\text{inj}}\left(x,t\right)$$

where V_m is the membrane potential at location x and time t, V_rest the resting potential, r_m the membrane resistance of unit length cable, and c_m the membrane capacitance per unit length. We observe that i_m, i.e., the source term of extracellular signals such as the EAP (Holt and Koch 1999; Gold et al. 2006; Anastassiou et al. 2013), is proportional to the temporal derivative of V_m, which, in this case, can be approximated by the intracellular potential, V_i. One important implication is that the timing of the positivity of the intracellular spike does not coincide with the EAP negativity. Assuming resistive extracellular conductivity, it follows that i_m is the source of the V_e signal so that i_m and V_e are completely in phase. It also follows that V_i (V_m) and i_m have an RC-type relationship, i.e., there is a phase between them. Thus, in terms of timing, V_i (or V_m) and V_e will not be in phase (e.g., see Figs. 2 and 4B). In fact, the EAP negativity from a signal recorded close to the soma broadly corresponds to the maximum rate of rise of the intracellular spike and thus typically precedes the intracellular spike positivity (see Fig. 6 and Buzsáki et al. 1996; Henze et al. 2000). Further away from the soma, electrogenesis of local membranes can impact the EAP waveform so that the time correspondence between EAP and intracellular somatic spike features may become further obscured. In addition, experimentally, the similarity between the EAP waveform and the temporal derivative of V_i remains qualitative especially after the initial phase of the action potential generation casting the V_i derivative as a rather coarse approximation of the EAP waveform.

Spike contribution to the LFP.

Unit activity is traditionally thought to impact the high-frequency (above 500 Hz) spectrum of extracellular recordings. The lowpass-filtered part of the extracellular signal, the so-called LFP, has historically been considered to mainly reflect a combination of postsynaptic activity and associated currents such as return currents as well as other processes such as oscillatory membrane and calcium-dependent currents (Mitzdorf 1985; Logothetis et al. 2007; Buzsáki et al. 2012; Einevoll et al. 2013). Recent computational and experimental studies have challenged this picture by showing that spike currents can impact bandwidths of the extracellular signal in the traditional LFP band (below 100 Hz; Rasch et al. 2009; Ray and Maunsell 2011; Belluscio et al. 2012; Zanos et al. 2011; Schomburg et al. 2012; Reimann et al. 2013; Waldert et al. 2013). Although interpretation of single-neuron CSD analyses is somewhat ambiguous, our experiments are in agreement with simulations (Pettersen and Einevoll 2008; Schomburg et al. 2012) showing that extracellular spikes can impact bandwidths lower than 200 Hz. Yet, the extent to which spiking can impact LFP characteristics has remained speculative. Our intracellularly induced spikes show that EAPs and spike afterpotentials of L4 and L5 pyramids can contribute spectral power as low as 20 Hz compared with nonspiking V_e traces. The effect of EAPs in such low frequencies is attributed to the slower, smaller amplitude repolarization typically difficult to distinguish in vivo although synaptic currents may also influence the EAP waveform in such time scales (Glickfeld et al. 2009).

What are the functional and computational ramifications of this observation? Spike-field coherence (with certain LFP bandwidths) is often used to infer the relationship between synaptic input (considered to be reflected in the lower LFP bands) and neural output (spiking) (Fries et al. 1997; Womelsdorf et al. 2006; Montgomery et al. 2008; Rutishauser et al. 2010; Anastassiou et al. 2011). Yet, if spiking itself can impact bands as low as beta or gamma, i.e., LFPs in these bandwidths are also shaped by spiking, then the causal relationship between LFPs (as a proxy to synaptic input) and spiking becomes questionable (Billeh et al. 2014; Anastassiou and Koch 2015; Schaub et al. 2015). On the other hand, clearly, synaptic currents are required to elicit spiking and will impact LFPs. The extent to which spiking and LFP (even in low bands) are independent is thus state dependent (for example, slow vs. fast background spiking) and measures such as spike-field coherence need to be assessed accordingly.

GRANTS

This work was funded by the Swiss National Science Foundation (to C. A. Anastassiou), the Human Frontier Sciences Program (to C. Koch, G. Buzsáki, and H. Markram), the National Institute of Neurological Disorders and Stroke (to C. Koch), and the Mathers Foundation (to C. Koch). C. A. Anastassiou and C. Koch thank the Allen Institute founders, P. G. Allen and J. Allen, for support.

DISCLOSURES

Conflict of interest statement: No conflicts of interest, financial or otherwise, are declared by the author(s).

AUTHOR CONTRIBUTIONS

Author contributions: C.A.A. and R.P. conception and design of research; C.A.A. and R.P. performed experiments; C.A.A. and R.P. analyzed data; C.A.A., R.P., G.B., and C.K. interpreted results of experiments; C.A.A. and R.P. prepared figures; C.A.A., R.P., G.B., and C.K. drafted manuscript; C.A.A., R.P., G.B., H.M., and C.K. edited and revised manuscript; C.A.A., R.P., G.B., H.M., and C.K. approved final version of manuscript.