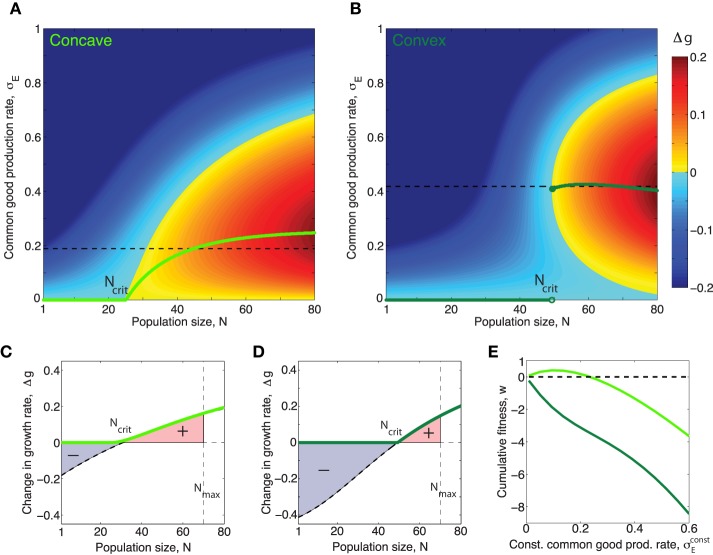
Figure 3.

Concave/convex benefit curves result in continuous/discontinuous optimal production curves respectively. (A,B) Green curves show optimal production rate of public good, ${\sigma }_E^{opt}$ as a function of population size, N for the concave/convex benefit functions shown in figure 1. The optimal value, ${\sigma }_E^{opt}(N)$, corresponds to the σ_E which maximizes Δg for N. The magnitude of Δg in the (N, σ_E)-space is shown by the colorbar. (A) In the case h = 1 the optimal production function is continuous and can be put in closed form: ${\sigma }_{E,h=1}^{opt}(N)=$ $max(\sqrt{(\beta K_E{\gamma }_E)∕(cN)}-(K_E{\gamma }_E)∕N,0)$, where β = β₁ + β₂. The critical population size above which public good production is nonzero, when h = 1 is: $N_{crit}=\frac{c}{\beta }{\gamma }_E{K}_E$. (B) When the benefit curve is convex, h = 2, the optimal production function is discontinuous. (C,D): Light/dark green curves show the effect on growth rate Δg for a population producing common good at exactly the optimal rate when the benefit curve is concave/convex respectively. Black dashed curves show the effect on growth rate Δg for a population producing common good at a constant rate ${\sigma }_E^{const}=1∕(N_{max}-N_{crit}){\Sigma }_{N_{crit}}^{N_{max}}{\sigma }_E^{opt}(N)$, equal to the average of the non-zero part of the optimal curve, (shown as black dashed lines in (A,B). (E) The cumulative fitness, $w\equiv ({\int }_1^{N_{max}}\Delta g(N)dN)∕w_{max}$, where $w_{max}\equiv {\int }_1^{N_{max}}\Delta g^{opt}(N)dN$, (def. in Equation fitnessDef) of different constant production strategies for a common good with concave (light green) and convex (dark green) benefit functions respectively. Note that in the case of the “concave common good” there is a range of different constant production rates which allows the population to perform better than a nonproducing population w > 0, however for the “convex common good” any constant production strategy will leed to worse fitness than that of a nonproducing population, w < 0 for all ${\sigma }_E^{const}>0$. (In this figure σ_E is given in units of κ∕γ_E, which was set to one).