Fig. 7.

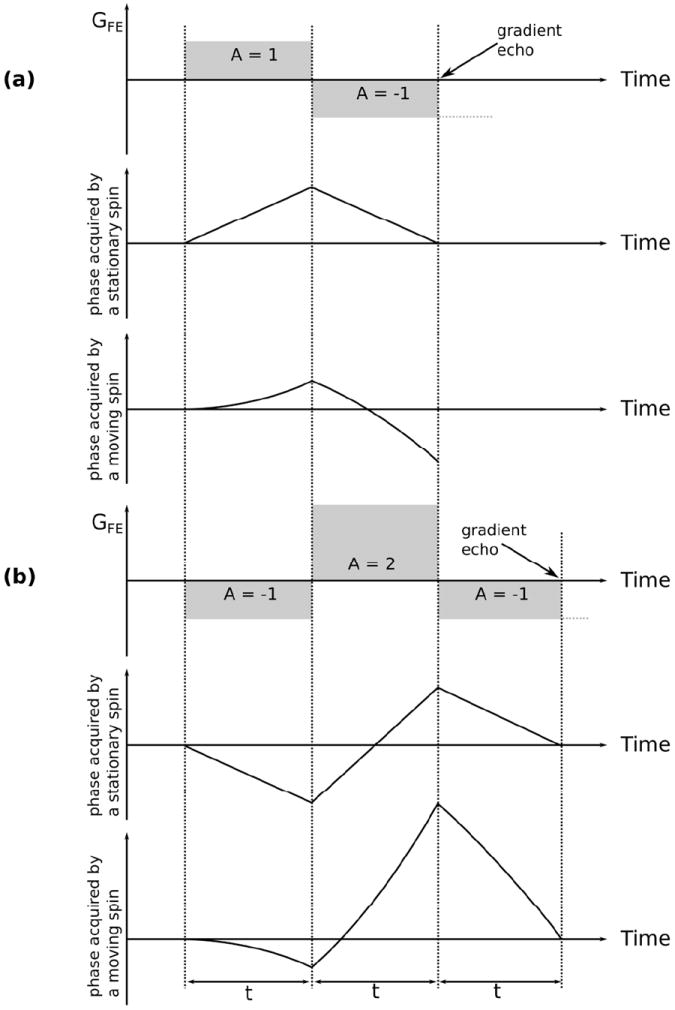
The effect of linear motion on the phase acquired by the spins under the action of the encoding gradients (frequency encoding in this example). A bipolar gradient (a) refocuses the stationary spins at the moment when the net area under the gradient arrives to zero. This is because the phase accrual in this case is proportional to a product of the gradient amplitude and the time duration. Contrary to that, the phase acquired by a spin moving along the gradient direction is proportional to the gradient amplitude, duration and the displacement of the spin. Because the displacement under the continuous motion is proportional to the time, the phase shows a quadratic dependency on time. Therefore, a bipolar gradient fails to refocus moving spins. Consequently, such spins will be poorly located and a motion artefact will be seen in vascular structures and moving fluids. It is possible to account for the quadratic behaviour of the phase by introducing a third gradient lobe, as shown in (b). Here, in order to keep the polarity of the frequency encoding gradient the sign of the two preceding lobes has been adjusted. The gradient area ratio of 1:-2:1 does not induce additional dephasing for the stationary spins and allows for refocusing the spins moving with a constant velocity. Other gradient schemes are possible taking into account gradient amplitude and slew rate limits, but velocity compensation always increases the minimal echo time.