SUMMARY
We examine carefully the numerical accuracy and computational efficiency of alternative formulations of the finite-element solution procedure for the mono-domain equations of cardiac electrophysiology (EP), focusing on the interaction of spatial quadrature implementations with operator splitting, examining both nodal and Gauss quadrature methods, and implementations that mix nodal storage of state variables with Gauss quadrature. We evaluate the performance of all possible combinations of “lumped” approximations of consistent capacitance and mass matrices. Most generally we find that quadrature schemes and lumped approximations that produce decoupled nodal ionic equations allow for the greatest computational efficiency, this being afforded through the use of asynchronous adaptive time-stepping of the ionic state-variable ODEs. We identify two lumped approximation schemes that exhibit superior accuracy, rivaling that of the most expensive variationally consistent implementations. Finally we illustrate some of the physiological consequences of discretization error in EP simulation relevant to cardiac arrhythmia and fibrillation. These results suggest caution with the use of semi-automated free-form tetrahedral and hexahedral meshing algorithms available in most commercially available meshing software, which produce non-uniform meshes having a large distribution of element sizes.
1. INTRODUCTION
The electrophysiology (EP) of cardiac tissue is commonly modeled as the solution of a reaction-diffusion boundary value problem [1, 2] governing the diffusion of electrical potential driven by local ionic currents produced at the single-cell level by the gating of ion channels. Among the numerical methods employed to approximate these analytically intractable equations, the finite element method (FEM) [e.g., 3–6] has become commonly favored, primarily because it allows to capture the curved geometry of the heart in a straightforward way. Also, because FEM is also the method of choice for solid mechanics, it has been noted that the framework provides a straightforward way to develop coupled simulations of electrophysiology and contractile mechanics of the heart [7].
The cardiac reaction-diffusion equations are of multiscale nature, with variations occurring at both scales associated with both the tissue and individual cells, both in time and space. The simplest discretization schemes — e.g., forward-Euler time-stepping with uniform mesh spacing — require extreme computational cost to attain stability and accuracy, making it difficult to achieve reasonable solution times for realistic problem domains and analysis durations even on the world’s largest computers. This has motivated tremendous efforts to find ways to speed up calculations.
Empirical studies seem to indicate that the spatial limitations on accuracy for cardiac EP simulation are determined fundamentally by the characteristic width of the pseudo wave front, a length scale that emerges from the ratio of the electrical conduction velocity to the rise time of the cardiac action potential. Recommendations for maximum element sizes range from 0.01 cm [8] to 0.02 cm [3, 9].† Convergence studies informing these guidelines generally rely on regular simulation domains and simple electrical activation patterns. The effects of discretization error for non-uniform physiological activation sequences in whole-heart simulation domains are less well studied.
Strategies that have been employed to address the multiscale features of the cardiac EP problem can be decomposed into roughly two categories: spatial discretization, and temporal discretization. Recognizing that the key length scale is associated with the rise of the action potential, some researchers have developed approaches to adaptively refine in both space and time [8, 10, 11]. While these temporally adaptive refinement schemes do reduce computational cost, they do so at the expense of greatly increased algorithmic and implementation complexity. A much simpler approach designed to save computational effort is to simulate on non-uniform finite element meshes specially tailored to resolve anatomical detail. For example, specialized automatic mesh generation techniques have been developed for the cardiac EP problem [4, 12], wherein a coarser mesh of regular node spacing in the tissue interior is automatically refined near boundary surfaces to capture anatomical features, generating meshes with element sizes that can differ as much as an order of magnitude. While this is rigorously justified in the context of solid mechanics, where computational error is provably greatest near boundaries of complex geometry where stress gradients are largest, such mathematical guarantees are not generally available in the case of electrophysiology.
Perhaps the simplest strategy for adapting to the temporal multiscale character of the problem is operator splitting, which separates the slow diffusion process from the fast ionic process [3, 13, 14]. The key benefit of this separation is that it isolates the integration of cardiac action potentials into a spatially-uncoupled system. Because the fastest time-scales of the problem are associated with the action potential, both adaptive time-stepping and more sophisticated local implicit schemes specific to the cardiac ODEs [15] can be used on a point-by-point basis to greatly reduce computational cost.
While the ODEs characterizing the ionic model can be solved in principle using any ODE solver, the choice for time-discretization is strongly influenced also by how the cell model ODEs are coupled back to the diffusion PDEs [9]. In particular, the ionic ODE state variables and currents can be defined and computed either at the nodes of the finite element mesh or alternatively at the Gauss quadrature points in the interior of the elements. For schemes using operator splitting [2, 10, 13] because the ionic current is only needed at the nodes, all ionic state variables can be stored as nodal variables, and the ionic ODEs can be solved as uncoupled nodal equations. However, in a more general scenario where both reaction and diffusion terms are discretized by finite element interpolation, [16–19], ionic currents need to be computed at the quadrature points of the mesh. There is a question of which variables are defined at the nodes and interpolated to quadrature points. The use of interpolation scheme can lead to significantly different numerical results in cardiac electrophysiology modeling in particular the conduction velocity of the electrical wave. Pathmanathan, et al. [9] define all state variables (voltage, ionic concentrations, gating variables, etc.) as nodal quantities, and consider two approaches for obtaining currents at the quadrature points.
Ionic current interpolation (ICI): Interpolate the ionic currents from the nodes inside the element and
State variable interpolation (SVI): Interpolate the state variables of the cell model into the interior of the element and compute ionic current using these interpolated values.
SVI is the most accurate, but is associated with a high computational cost and increased storage requirements, whereas ICI is relatively inexpensive, but less accurate. On the other hand, observing that spatial gradients of ionic state variables (concentrations, gating variables) are not needed, Göktepe, et al. [6, 7, 20] avoid the need for interpolation by storing these internal variables at the quadrature points. So far no direct comparison has been made between these nodal-variable and internal-variable approaches.
It is noteworthy that operator splitting is the only approach that provides explicit spatial decoupling of the ionic ODEs and state variables. Hence, it is the only technique that allows for “embarrassingly parallel” adaptive time-stepping. However, the common drawback cited for operator splitting is the difficulty of ensuring numerical stability of the resulting scheme [21]. Moreover, to achieve numerical accuracy comparable to that of the most accurate interpolating schemes (SVI, [9]), operator-splitting approaches have so far required finer mesh sizes.
The goals and results of this paper follow a two-part structure. First, we aim to understand the effects on numerical accuracy and computational efficiency of operator-splitting formulations produced by storing ionic state variables either at the nodes or at internal quadrature points, and specifically to discover whether the efficiency of adaptive operator splitting may be combined with the enhanced accuracy provided by interpolation techniques such as SVI and ICI. Toward this first goal we introduce operator splitting as a post-discretiztion solution technique, and show how this approach produces several options for incorporation alternative interpolation techniques introduced by Pathmanathan, et al. [9]. In particular, we study the effects of so called “matrix lumping” techniques on numerical convergence of formulations using operator splitting. We test the different formulations on a benchmark problem recently proposed by Niederer, et al. [22], and quantitatively compare the convergence rates using a 3D cable geometry. The second aim of this paper is to expose some of the physiological consequences of excessive numerical discretization error. The standard tests of numerical accuracy for cardiac EP simulation in the literature tend to focus on convergence of activation times and conduction velocities in simple cable like geometries with uniform meshes. However it remains unclear what the practical impact of insufficient refinement is in physiologically realistic domains, which often require a distribution of element sizes, and always produce nontrivial activation sequences. Therefore we close the paper by examining some physiological artifacts produced by discretization error in nonuniform meshes when simulating planar wave propagation and spiral wave break up in 2D domains.
2. FEM FORMULATIONS OF CARDIAC EP
Here we develop in detail the weak form and finite element discretization of the monodomain equations [1] of cardiac EP. Although we ultimately wish to employ a split of the reaction and diffusion terms in these equations for the sake of numerical implementation, we develop the formulation in coupled form and apply the split to the discretized equations to allow for a more direct comparison of split and coupled implementations.
2.1. Governing Equations
Let Ω ∈ ℝ3 denote the region occupied by the cardiac tissue. We model the transmembrane voltage V (x, t) as governed by the monodomain equations
| (1a) |
| (1b) |
where σ is the conductivity tensor, Cm is the capacitance across the membrane, χ is the surface area to volume ratio and
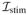 is the stimulus current. u are set of cell-level variables whose dynamic behavior is governed by the ODEs given by f and they couple back to the PDE through the ionic current
is the stimulus current. u are set of cell-level variables whose dynamic behavior is governed by the ODEs given by f and they couple back to the PDE through the ionic current
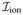 . The single-cell ionic current is commonly modeled using the Hodgkin-Huxley framework [1], describing the electrical activation potential of an excitable cell according to the solution of a set of nonlinear ODEs. The identities of the ionic variables describing the gating of specific channels, as well as the choice of specific functional forms for f(u, V), are determined empirically according to careful experimental measurements of channel properties using patch-clamp techniques. For the sake of computational efficiency, the ionic response is sometimes modeled using crude phenomenological models like the two-variable Fitz-Hugh Nagumo model which exhibit the general characteristics of an excitable cell but fail to reproduce the physiologically important features such as the sharp increase in voltage during the depolarization phase. There also exist more realistic models, such as Luo-Rudy-II [23] and the UCLA model [24], which are preferred for computational and physiologically accurate simulations.
. The single-cell ionic current is commonly modeled using the Hodgkin-Huxley framework [1], describing the electrical activation potential of an excitable cell according to the solution of a set of nonlinear ODEs. The identities of the ionic variables describing the gating of specific channels, as well as the choice of specific functional forms for f(u, V), are determined empirically according to careful experimental measurements of channel properties using patch-clamp techniques. For the sake of computational efficiency, the ionic response is sometimes modeled using crude phenomenological models like the two-variable Fitz-Hugh Nagumo model which exhibit the general characteristics of an excitable cell but fail to reproduce the physiologically important features such as the sharp increase in voltage during the depolarization phase. There also exist more realistic models, such as Luo-Rudy-II [23] and the UCLA model [24], which are preferred for computational and physiologically accurate simulations.
Let the boundary of the domain be denoted ∂Ω, with outward unit normal n(x, t). The potential is assumed to satisfy a no-flux boundary condition on ∂Ω,
| (2) |
where
denotes the spatial partial derivative, and summation is implied in the repetition of indices. To generate the weak form of the boundary value problem formed by eqns. (1) and (2), we form the weighted residual for some admissible weight function ψ, and integrate by parts using the divergence theorem to obtain,
| (3) |
Due to the no flux boundary condition the surface integral vanishes. Furthermore, as is customary we can combine the stimulus and the ionic currents into a single current term
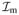 =
=
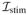 − χ
− χ
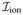 , yielding the weak form as
, yielding the weak form as
| (4) |
∀ ψ admissible.
2.2. Finite Element Discretization
The domain is discretized into a set of subdomains (finite elements). In a standard isoparametric formalism, position within each element is parameterized by a set of curvilinear or natural coordinates . The positions and voltage are interpolated among nodal values using piecewise polynomial shape functions Na(sα),
| (5) |
| (6) |
| (7) |
where xia denotes the ith coordinate of the node a and Va denotes the voltage at nodes a. The test functions are also expanded in the basis provided by these shape functions
where ψa are arbitrary nodal weights. Substituting these relations into the weak form of eqn. (4) produces
| (8) |
Since ψa are arbitrary, their coefficients must then also be zero
| (9a) |
or
| (9b) |
where
| (10) |
| (11) |
| (12) |
| (13) |
Here Ia is interpreted as the consistent nodal transmembrane current at node a, Cab are the components of the capacitance matrix, and σab are the components of the conductance matrix. The components of the conductance matrix require gradients of the shape functions. The spatial gradients of the shape functions are then computed by the chain rule as
| (14) |
2.3. Numerical Quadrature and Matrix Lumping
In the semi-discrete finite element equations (9–13), spatial integration is performed over the entire domain, by global assembly of individual element integrals. In the standard form of numerical integration, evaluation of the integrand is done at the Gauss-Legendre quadrature points inside every element. We will refer to this as Gauss integration. Let and ŵp, p = 1, …, Q be the quadrature points and weights, such that
Also, denote J ≡ det[Jiα], such that dv = Jd3s. The nodal ionic current computed by Gauss quadrature is
| (15a) |
and the capacitance and conductivity matrices are
| (15b) |
| (15c) |
where
are the effective quadrature weights for material and spatial integrals. Because the capacitance and conductivity matrices involve integrals of polynomial shape functions, Gauss quadrature of sufficiently high order provide exact results. However for the consistent nodal ionic currents, we expect results to generally depend on how the local current
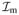 is computed at the quadrature points.
is computed at the quadrature points.
2.3.1. Internal State Variables at Gauss Points
In the case where ionic variables are defined as internal variables, stored directly at the quadrature points, as in [6, 7, 20], then the evaluation of eqn. (15a) is unambiguous. Explicitly, the current at a Gauss point sp is computed using the internal variables up stored at that Gauss point, and voltage interpolated at Gauss point as per eqn. (6),
Because the interpolated voltage depends on surrounding nodal values via eqn. (6), it is clear that in this approach integration of the local internal ODEs is coupled to that of the global PDEs. Specifically, this makes it difficult to construct time-stepping schemes for the internal variables with time steps independent of that of the global nodal voltages.
2.3.2. Nodal State Variables
The alternative is to define ionic state variables as nodal variables, ua. To evaluate current at Gauss points, Pathmanathan, et al. [9] classified the approaches in the previous literature by the following two categories.
State Variable Interpolation
The SVI approach is to interpolate the state variables to the Gauss points
and then to evaluate the ionic current using interpolated state variables and voltage as
This interpolation imposes a significant CPU cost (as well as storage demands) to compute the additional Gauss-point values of the state variable array u, which can have as many as 40 or more components for advanced cell models [24].
Ionic Current Interpolation
One alternative to SVI is the ICI approach, which computes current densities from the nodal state variables,
and interpolates these to the Gauss points,
| (16) |
or
| (17) |
where
| (18) |
are referred to as the components of the “mass matrix”
and
is the vector of nodal current densities.
2.3.3. Nodal Quadrature
When state variables are stored along with voltages at the finite element nodes, an alternative approach to the SVI and ICI interpolation methods is to compute the nodal ionic currents by nodal quadrature. This approach places quadrature points at the nodes, with quadrature weight va representing the volume associated with node a. By the Kronecker-delta property of the shape functions, Na(xb) = δab, the nodally integrated currents become
| (19) |
where, Ia =
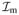 (Va, ua) are currents computed from nodal state variables. Nodal quadrature is most closely related to ICI, in that both methods compute the consistent nodal currents Ia as linear combinations of the currents evaluated based on nodal state variables. In fact, the nodal quadrature result can be considered as a special case of the ICI result, in which the mass matrix is diagonal, Mab = δabva (no sum). Indeed, this is precisely what one obtains by performing a row-sum lumping approximation of the “full” or consistent mass matrix,
(Va, ua) are currents computed from nodal state variables. Nodal quadrature is most closely related to ICI, in that both methods compute the consistent nodal currents Ia as linear combinations of the currents evaluated based on nodal state variables. In fact, the nodal quadrature result can be considered as a special case of the ICI result, in which the mass matrix is diagonal, Mab = δabva (no sum). Indeed, this is precisely what one obtains by performing a row-sum lumping approximation of the “full” or consistent mass matrix,
where va = ∫ΩNadv can be interpreted as the volume of node a. As considered by Pathmanathan, et al. [25], the ICI approach can be combined with lumping for either the mass matrix, the capacitance matrix (Cab = χCmMab), or both, with varying effects on accuracy. In particular, lumping of the capacitance matrix is especially convenient when explicit time-stepping schemes are used to increment the nodal voltage solution, as it avoids the need to solve a linear system. This is particularly attractive when combined with operator splitting, as we discuss below.
2.4. Time Discretization Schemes with Operator Splitting
As first applied to the monodomain EP problem by [13], operator splitting techniques provide a straightforward way of dealing with multiple temporal scales. If we employ Strang splitting, as proposed by [13], which is second-order accurate (provided that the discrete time-integration methods for in each operator is also second-order accurate and also the applied stimulus is time independent), then the monodomain PDEs of eqn. (1a) are solved by alternating time-integration of diffusion and ionic operators
| (20) |
The split, as indicated by eqn. (20), is commonly applied to the undiscretized differential operators. If implemented in this traditional way, the diffusion operator in eqn. (20) will need to be discretized in space with finite elements, leading to semi-discrete equations of the form,
| (21) |
On the other hand, in such an implementation the operator split naturally separates the ionic equations into spatially decoupled, local, ordinary differential equations. In other words, because no spatial gradients appear in the ionic updates in eqn. (23b), those equations do not need to be cast into a weak form and discretized with finite element shape functions — spatial discretization then trivially entails applying these equations at the finite element nodes, i.e.,
| (22a) |
| (22b) |
where they can be discretized in time and solved directly.
Post-discretization Splitting
Here we choose instead to apply the operator split after performing the finite element discretization (see Algorithm 1). That is, the operator split is applied to the semi-discrete finite element equations (9). For the diffusion terms in the equations, the distinction is without a difference — both pre- and post-discretization operator splits lead to the same linear system of ODEs in eqn. (21). For the ionic terms in the problem, however, if prior to performing the operator split we first apply the spatial finite-element discretization to the weak form of the governing equations, the ionic part of the split is represented by equations of the form
Algorithm 1.
Qu-Garfinkel Operator Split [13].
| Global time loop | ||||||
for step n = 1 … nmax
do
| ||||||
| end for |
| (24a) |
| (24b) |
In this case, the vector of nodal currents I can be computed by Gauss quadrature with state variables stored at quadrature points, or by either SVI or ICI with state variables stored at the nodes, as described in the previous section. The ICI approach, moreover, allows for multiple variants, by selective lumping of C and/or M. Pathmanathan, et al. [25] considered two choices for matrix lumping without operator splitting: in what was termed full lumping, the capacitance and mass matrices are both lumped, whereas in half lumping only the capacitance matrix is lumped. However, as we discuss below, operator splitting of the ICI-formulated equations effectively expands the number of options, allowing for selective lumping of three matrices: a capacitance in the diffusion part of the split, and a capacitance and mass in the ionic part. As we will demonstrate, inconsistent lumping of the capacitance in the two parts of the split can yield surprising improvements in numerical accuracy over the standard full and half lumped un-split approaches.
2.5. Matrix Lumping with ICI
Introducing the ICI current definition (17), the operator-split FE equations (21) and (24a) take the form
| (25a) |
| (25b) |
We consider six distinct variants of the operator splitting algorithm combined with ICI. These variants correspond to selective lumping of any of three matrices: C in the diffusion update (26), and C and M in the ionic update (24). While selective lumping of these three matrices generates 23 = 8 total options, we show that certain combinations are equivalent, making for a total of six distinct variants. For the sake of conciseness, we will refer to the variants using a compact, three-character labeling convention described in Table I.
Table I.
Summary of the eight variants of Ionic Current Interpolation combined with operator splitting.
| Label | Diffusion Part | Ionic Part | ||
|---|---|---|---|---|
| C | C | M | ||
|
| ||||
| 1. | F-FF | full | full | full |
| 2. | ≡ F-LL | full | lumped | lumped |
|
| ||||
| 3. | L-FF | lumped | full | full |
| 4. | ≡ L-LL | lumped | lumped | lumped |
|
| ||||
| 5. | F-LF | full | lumped | full |
|
| ||||
| 6. | L-LF | lumped | lumped | full |
|
| ||||
| 7. | F-FL | full | full | lumped |
|
| ||||
| 8. | L-FL | lumped | full | lumped |
Diffusion updates
For the diffusion step in the operator split, the choice to be made is whether or not to use the lumped approximation to the capacitance matrix. As is the case in structural dynamics, the main motivation for the lumping approximation is to render the capacitance a diagonal matrix, so that its inversion becomes trivial. This is mainly desired when explicit time-stepping strategies are use. If, for the sake of stability or accuracy (or both), implicit time-stepping is performed, requiring the solution of a non-trivial linear system, then a diagonal capacitance may have little impact on execution time. It is unclear a priori whether a full or lumped capacitance will lead to greater accuracy.
Ionic updates
For the ionic step, any combination of the capacitance and mass matrices may be lumped. The four cases are as follows:
-
LL. With both of the matrices lumped, the ionic update equation becomesBecause va ≠ 0, the ionic equations reduce to the uncoupled form
Clearly the fully lumped ionic solve is equivalent to nodal integration, which is tantamount to solving the strong form of the operator split equations (22) directly at the nodes. This is the widely used choice [2] owing to two key computational benefits. First, because the capacitance matrices are diagonal, explicit time stepping for the voltage is made very efficient in both the diffusion and ionic solves. Secondly, because the ionic step is purely local (i.e., involving only quantities at single nodes) it allows for “embarrassingly parallel,” uncoupled time-stepping of the nodal equations, without any communication among processors in a distributed computing environment. This makes it possible to implement asynchronous adaptive time-stepping schemes, with integration of each node’s ionic equations advancing from tn to tn+1 = tn + Δt through a sequence of sub-time steps, τk, k = 1, …, K, τK − τ1 = Δt, with Δτ = τk+1 − τk adaptively determined, for instance by the rate of change of nodal voltage [13].
Full lumping in the ionic part of the split can be combined with either of two options for the diffusion part, a full capacitance (F-LL) or lumped capacitance (L-LL). The latter choice, in which all matrices in both parts are lumped, corresponds to what Pathmanathan, et al. [25] term full lumping. This is the standard choice used in codes that employ explicit time-stepping for the voltage. In the partially lumped (F-LL) option, the full capacitance in the diffusion part makes it necessary to use implicit schemes for voltage updates. However, because capacitance lumping contributes error to the solution[25], we anticipate that this error might be mitigated by using the full capacitance in the diffusion part, while retaining a lumped capacitance in the ionic update in order to enjoy the advantages of asynchronous adaptive time stepping.
-
FF. The capacitance and mass in the ionic part are both full. The ionic update equation then becomesBut again since M ≠ 0 the ionic equations uncouple to
Thus this scheme turns out to be equivalent to CLML. We see then that two of the eight lumping combinations are redundant: F-FF≡F-LL and L-FF≡L-LL. This seemingly trivial result has surprising and important implications. It means that when operator splitting is employed, full lumping of the ionic part will yield solutions every bit as accurate as no lumping at all. This is in stark contrast to the situation without operator splitting [25], where full lumping produces significant error. The apparent inconsistency suggests that perhaps the source of the error incurred by lumping is tied to the diffusion terms in the governing equations. We return to this point subsequently in the discussion of numerical studies below.
-
LF. Lumping of the capacitance but not the mass matrix is akin to the half lumping approach described Pathmanathan, et al. [25]. In this case the ionic part becomesThe ionic solve is no longer interpretable as purely local, node-by-node integration of ionic ODEs. The nodal ionic equations are not uncoupled as in the above cases. A particularly important consequence of the coupling generated by a full mass matrix is that during the ionic solve, the complete set of nodal ODEs, including the state variables,
must be integrated synchronously. That is, asynchronous adaptive time stepping strategies, such as that of [13], cannot be employed when the ionic mass matrix is full. Thus the nodal equations (21) and (24) must be integrated simultaneously at a single fixed time step. This, in large part, defeats the main purpose of operator splitting, to algorithmically decouple the numerically stiff ODEs from the (non-stiff) parabolic PDEs. On the other hand, one remaining advantage to this approach is that it enables explicit time-stepping of the voltage, especially when combined with lumping in the diffusion part (L-LF), which is essentially a split version of the half lumping scheme in [25]. This being the case, we expect accuracy to be improved relative to the fully lumped case (L-LL).
-
FL. This combination represents a sort of inverted half lumping. The ionic equations become
The full capacitance now prevents both explicit time stepping of the voltage and asynchronous adaptive time stepping of the state variables. Thus we expect less computational efficiency from the two schemes stemming from this choice, F-FL and L-FL.
Therefore, we have six distinct variants of the ICI scheme, denoted by character codes as summarized in Table I. In the following section, we assess the accuracy and convergence properties of these six schemes through a series of benchmark numerical studies.
3. BENCHMARK STUDIES
Here we present the results of numerical benchmark studies comparing the assortment of computational formulations considered in Section 2.
3.1. Comparison of Gauss Quadrature and Nodal Quadrature
As explained above, finite implementations of the cardiac EP problem can be sorted into two categories, based on whether “internal” ionic model variables are stored at (Gauss) quadrature points, or at nodes. To assess the differences between these two strategies, we simulated unidirectional electrical conduction in a 2D block of dimension 2.5 cm by 0.5 cm, meshed using standard 4-node quadrilateral elements with bilinear Lagrange interpolation. A stimulus current of 20, 000μA/cc was applied to a region from the left end up to 0.1 cm for 5 ms. For both approaches, full-order Gauss quadrature was used to integrate all diffusion terms. The consistent ionic nodal force current was calculated in two ways:
Nodal Quadrature Implementation
Ionic state variables were stored as nodal quantities ua, and nodal currents were computed as per eqn. (19), with the nodal integration weight defined as the nodal volume va = ∫ΩNadv (computed by Gauss quadrature). As discussed above, this is also equivalent to the so called “fully lumped” version of the ICI formulation.
Gauss Quadrature Implementation
State variables were stored at the Gauss points internal to each element, and consistent nodal currents computed according to the definition in eqn. (15a).
In both implementations, mass matrices were lumped and the equations integrated in time by explicit, forward Euler time-stepping with a single global time step of 0.001 ms, with no operator splitting. Mesh sensitivity was studied by varying the mesh size (i.e., element edge length) uniformly in both directions. The voltage was observed at a set of x locations (0.6, 0.8, 1.0, 1.2, 1.4, 1.6, 1.8 and 2.0 cm) with y = 0.25 cm. To calculate the conduction velocity, vh, linear regression was performed on the times at which the voltage crossed −40 mV at these locations. Figure 1(a) shows the conduction velocity as a function of mesh size for these two implementations. To estimate the error in the conduction velocity, values vh were compared to the result from a highly refined (Δx = 10μm) 1D finite-difference implementation, v* ≈ 52.81 cm/s. A log-log plot of the normalized errors (||vh − v*||/v*) is shown in Fig. 1(b). Near straight lines of slope ≈ 2 suggests roughly quadratic convergence.
Figure 1.
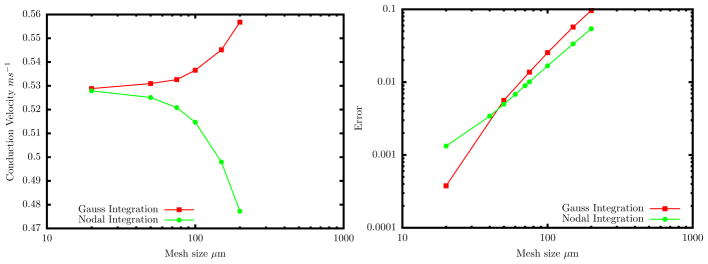
Variation in conduction velocity due to spatial discretization error. (a) The Gauss integration causes the velocity to increase with increasing discretization error while the nodal integration has reverse effect. (b) Errors in conduction velocity are computed as the normalized difference relative to the value from a highly refined 1D finite-difference implementation (Δx = 10μm). Convergence is roughly second order for both methods.
Apart from the fact that the Gauss-state-variable implementation converges above and the Nodal-variable implementation converges from below, the two methods show comparable accuracy. In the following, we shift focus squarely onto the later, to consider the performance of alternate matrix-lumping options with operator splitting.
3.2. Preferential matrix lumping schemes
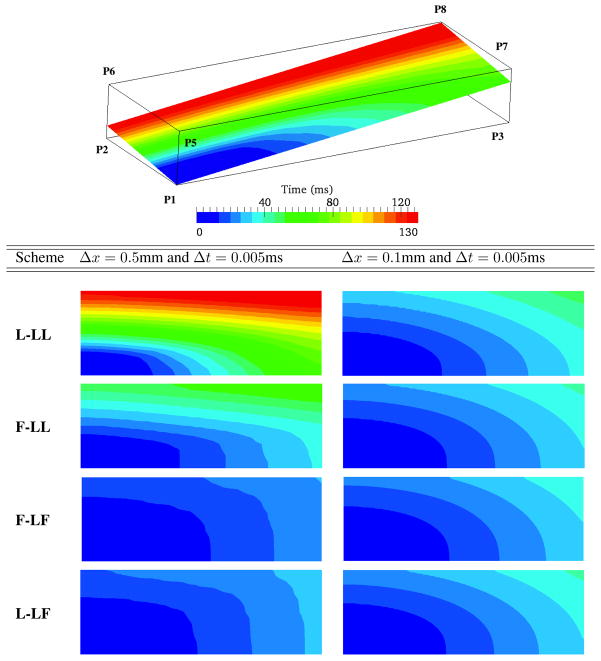
To assess the performance of the six distinct matrix lumping options in the split ICI formulation, we make use of the benchmark posed by Niederer, et al. [22]. As shown in Fig. 2 a rectangular block of dimension 2.0 × 0.7 × 0.3 cm defines the domain, with monodomain EP modeled by the Ten Tusscher Epicardial model [26]. Following [22] we set the Surface area to volume ratio as χ = 1400 cm−1 and the membrane capacitance as Cm = 1μF/cm2. Conduction is defined to be transversly isotropic, with the fast-conducting fiber direction set along the 2.0 cm edge of the box. The conductivity σ was chosen as 0.1334mS/cm along the fastest direction (X axis) and along the other two axis σ was 0.0176mS/cm. A stimulus current of 50, 000μA/cc applied for 2 ms to corner 1 of the block over a set of nodes contained in a 0.15cm3 cube. A sample mesh with element size 0.02cm is shown in Figure 2(b).
Figure 2.
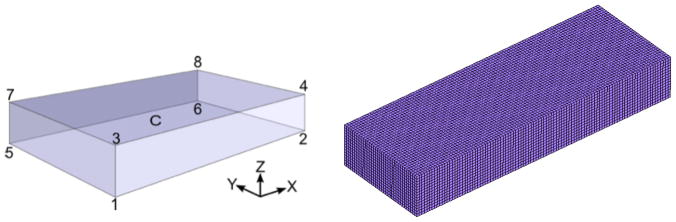
Rectangular domain from benchmark problem posed by Niederer, et al. [22]. (a) Schematic showing voltage sampling points. (b) Example mesh of trilinear hexahedral elements with uniform edge length of 0.02 cm.
We use operator splitting to solve the diffusion and ionic parts of the ICI-formulated EP equations separately, as developed in Section 2. The diffusion steps i) and iii) of Algorithm 1 are solved implicitly using Crank-Nicolson scheme. For instance, the step i) update takes the form
| (26) |
The ionic integration in step ii) is solved using the semi-implicit method introduced by Whiteley [16], wherein the new state variables un+1 are solved implicitly using the previous value of the voltage , followed by an explicit voltage update. We break the full time step Δt into a number of ionic sub-steps, {τ0 = tn, …, τk = τk−1 + Δτ, …, τK = tn+1}. The semi-implicit scheme solves allows relatively larger ionic sub-steps Δt than explicit schemes. The implicit solution for the diffusion part is computed by the Conjugate Gradient method with a Jacobi preconditioner as implemented in the Trilinos software package [27]. Trilinear 8-noded hexahedral elements were integrated with 2nd order (full) Gauss Quadrature.
The benchmark problem was solved using each of the six distinct operator-split matrix-lumping schemes summarized in Table I. In each solution, the times were recorded when the voltage reached 0 mV at each of the locations indicated in Figure 2(a). These results for the four best-performing schemes are listed in Table III in Appendix A. Results for the L-FL and F-FL schemes are not listed because solutions diverged for time steps greater than Δt = 10−5ms.
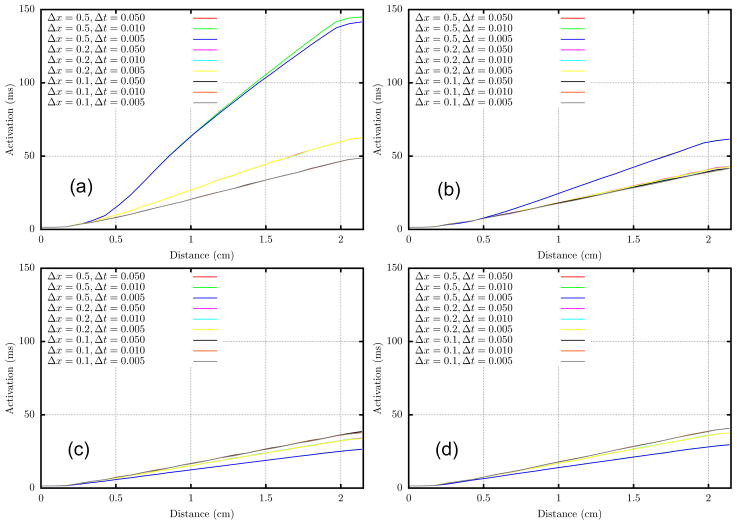
The activation times, as plotted along the straight line from P1 to P8 in Fig. 3, show very little sensitivity to time step for Δt ≤ 0.05 at all mesh sizes. However, results are sensitive to the mesh size. Roughly the data appears to follow two trends. First, for schemes with a lumped mass matrix, L-LL and F-LL, activation times tend to decrease as Δx decreases. Second, schemes with consistent mass matrices, F-LF and L-LF, yield activation times that tend to increase as Δx decreases. Judging by these trends it would appear that the F-LL and L-LF schemes are the most accurate for Δx ≤ 200μm. These two variants converge from opposite directions, and have values that agree within a few percent for the finest meshes. Moreover these two variants give the least mesh sensitivity.
Figure 3.
Activation time along the straight line connecting P1 to P8 for various mesh sizes and and time steps. (a) L-LL, (b) F-LL, (c) F-LF, and (d) L-LF.
One way to interpret the convergence trends is to recognize the use of a consistent mass matrix in the ionic half-steps as equivalent to Laplacian smoothing of the ionic currents. A simple example demonstrates that this is the case. Let us consider a 1-D cable of two-noded linear Lagrange elements. The mass matrix for each element is given by
| (27) |
The consistent nodal ionic currents are computed from nodal current densities as I = M
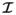 . After global assembly, this gives
. After global assembly, this gives
| (28) |
The global mass matrix can be decomposed as follows
or
where 1 is the identity matrix, β = Δx2/6, and
is the discretization of the Laplacian operator
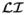 ≈ ∇2
≈ ∇2
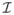 . Accordingly the operation I = M
. Accordingly the operation I = M
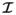 represents a Laplacian smoothing of the nodal currents. The ionic integration step in the operator split is equivalent to a discretization of the PDE
represents a Laplacian smoothing of the nodal currents. The ionic integration step in the operator split is equivalent to a discretization of the PDE
In other words, the numerical smoothing provided by the consistent mass matrix is interpreted as producing some algorithmic diffusion of the ionic currents. It follows that this artificial diffusion should augment the physical diffusion in the monodomain equations. An artificial increase in diffusion is consistent with observation conduction velocities increasing with mesh size for the full-mass L-LF and F-LF methods.
This interpretation may also help to explain why the L-FL and F-FL methods tend to diverge: in each of those cases the use of a consistent capacitance and a lumped mass produces the opposite of smoothing — what we might term sharpening. Explicit updates of the voltage then take the form Vn = Vn−1 + ΔtC−1ML
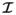 . Because the consistent capacitance has the same structure as the mass, it is also effectively a smoothing operator. Therefore C−1 acts as a sharpening operator, i.e., having the opposite effect of smoothing the nodal currents, presumably destabilizing the numerical solution.
. Because the consistent capacitance has the same structure as the mass, it is also effectively a smoothing operator. Therefore C−1 acts as a sharpening operator, i.e., having the opposite effect of smoothing the nodal currents, presumably destabilizing the numerical solution.
3.3. Wave speed convergence
The results from the benchmark problem from [22] allow for straightforward comparison of the ICI operator-split variants with each other and with other published solvers. To more systematically study the convergence of our implementations, we have also used them to solve for unidirectional wave propagation in a simple 3-D cable, as in Sec. 3.1. In particular we compare the two putatively most accurate schemes F-LL and LLF, with the fully lumped L-LL scheme most common in the literature and F-LF. A 3D cable of length 2 cm was used to study the effect of mesh size on these formulations. One end of the cable was stimulated for 5 ms by 50000 μA/cc. The activation times at several different locations in the cable (when V = 0mV) were recorded, and the conduction velocity (vh) was computed by linear regression. The conduction velocity for a mesh size of 10μm was chosen as the converged velocity (v*). Figure 4 shows the comparison between the usual consistent lumped formulation and the proposed formulation with preferential lumping. The plot confirms that the F-LL and LLF converge more quickly than the standard fully-lumped formulation L-LL. The time steps chosen were Δt = 0.1ms and Δτ = 0.01ms. The other key feature to take away from this plot is that beyond a mesh size of 200μm the wave speed is questionable even with the most accurate schemes. This is of importance while using automatic meshers to generate a mesh in a typical 3-D cardiac analysis. While the average element size might be less than 200 μm, any elements of size greater than 200μm may produce spurious local differences in conduction velocity.
Figure 4.
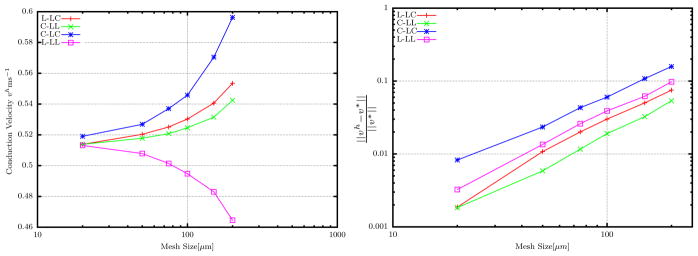
Convergence of different formulations. The plot on the right is plotted using log–log scale. All schemes show similar to convergence rates, however L-LL converges from the bottom while the other schemes from top and F-LF does not approach the converged value v*.
3.4. CPU efficiency
The choice about which formulation to employ hinges not only on accuracy, but also on the computational efficiency. To compare CPU times, we tested the two most accurate schemes F-LL and L-LF on uniaxial propagation in a 2-D bar 6 × 2 cm, meshed with a uniform element size of 200 μm. Nodes lying with 0.2cm of the left end of the bar were applied a stimulus current of 50000μA/cc for 5 ms. Nodes lying with 0.2cm of the left end of the bar were applied a stimulus current of 50000μA/cc for 5 ms. Conduction velocity was computed based on the activation times at at x = 0.5cm and x = 2.0cm. The L-LF scheme requires the global assembly of the ionic current vectors I = M
 in each sub-step of the ionic integration step Δτ. This global coupling of neighboring nodes makes asynchronous adaptive sub-stepping of the ionic updates impossible. Therefore this method was performed using uniform ionic sub-time steps. For the F-LL scheme on the other hand, a lumped mass matrix renders the nodal ionic updates completely decoupled, enabling asynchronous adaptive time stepping as noted above. We tested the method both with uniform ionic sub-time-steps, and with Δτ adapted for each node independently based on the the value of dV/dt, following Qu and Garfinkel [13].
in each sub-step of the ionic integration step Δτ. This global coupling of neighboring nodes makes asynchronous adaptive sub-stepping of the ionic updates impossible. Therefore this method was performed using uniform ionic sub-time steps. For the F-LL scheme on the other hand, a lumped mass matrix renders the nodal ionic updates completely decoupled, enabling asynchronous adaptive time stepping as noted above. We tested the method both with uniform ionic sub-time-steps, and with Δτ adapted for each node independently based on the the value of dV/dt, following Qu and Garfinkel [13].
Simulations using several different time steps (Table II) show that conduction velocity tends to increase as time steps are reduced. Accuracy appears to be slightly better for F-LL, with slightly higher (≈ 4%) conduction velocities than L-LF. CPU times (Table II) for the two methods differ by negligible amounts. To rationalize this, we note the two main differences between the methods: (i) L-LF requires a global assembly operation in each ionic sub-step whereas F-LL does not; and (ii) F-LL requires the solution of a linear system in each implicit diffusion sub-step, whereas L-LF does not. With the linear solution computed with a preconditioned conjugate gradient solver, both of these operations turn out to be order N in the number of nodes. Therefore it may not be surprising that computational costs are roughly equal. The one significant difference in performance between the two methods comes from employing asynchronous adaptive time-stepping for the ionic solve in F-LL: the final row of Table II shows that setting Δτ adaptively between 0.1 and 0.01 ms yields a CPU time roughly equal to that of a fixed Δτ = 0.01 ms simulation, but with accuracy closer to that of a fixed Δτ = 0.1 ms simulation.
Table II.
Comparison in CPU time between L-LF and F-LL schemes. Ionic sub-steps are uniform, except for the last row, where Δtau; is adapted asynchronously for each node independently following [13].
| Method | Δt (ms) | Δt (ms) | Conduction Velocity (m/s) | CPU time (s) |
|---|---|---|---|---|
|
| ||||
| 0.1 | 0.1 | 0.522 | 16.69 | |
| L-LF | 0.1 | 0.05 | 0.532 | 27.72 |
| 0.1 | 0.01 | 0.555 | 123.76 | |
| 0.1 | 0.1 | 0.536 | 17.06 | |
|
| ||||
| F-LL | 0.1 | 0.05 | 0.549 | 27.64 |
| 0.1 | 0.01 | 0.561 | 131.75 | |
| 0.1 | 0.01–0.1* | 0.543 | 18.113 | |
Last row, uses adaptive time-stepping, which is possible for F-LL but not for L-LF (see main text).
4. PHYSIOLOGICAL CONSEQUENCES OF MESH DEPENDENCE
One of the key observations from the convergence studies above is that for element sizes above ≈ 200μm the conduction velocity attained from most of the schemes is highly sensitive to mesh size. While for uniform meshes such as used in the above studies this mesh dependence produces noticeable quantitative errors, it can lead to even qualitative differences when applied to nonuniform meshes, i.e., containing elements with a non-uniform distribution of element edge lengths, as are commonly generated with automatic meshing software [12, 28, 29]. To get a sense for the mesh-dependence of our operator split schemes in more complex settings, we here simulate using non-uniform meshes (a) planar wave propagation and (b) the breakup of spiral waves as is found in ventricular fibriliation [e.g., 30].
4.1. Effect of mesh size on wave speed
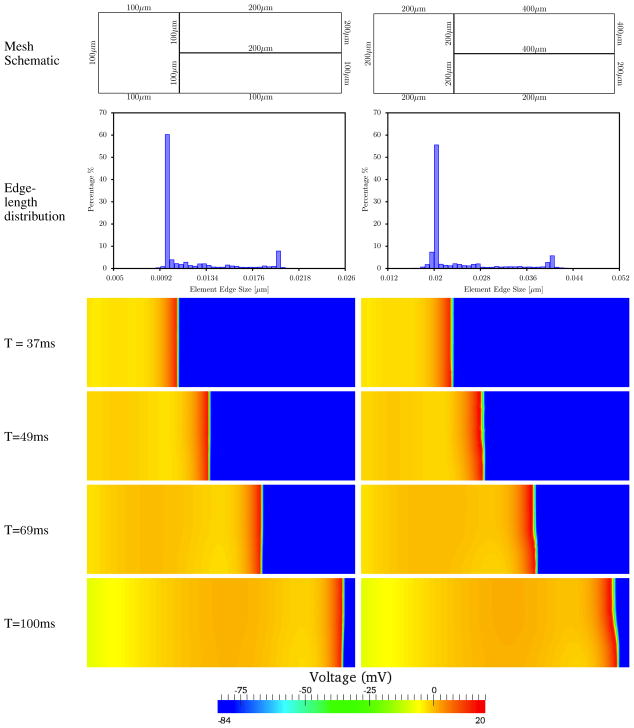
Here we consider unidirectional EP propagation in a 2D block 6cm × 2cm, meshed with a nonuniform quadrilateral mesh, and integrated with the L-LF scheme. Bilinear quadrilateral elements were used with second-order Gauss quadrature. To generate non-uniform meshes, the geometry was partitioned into three regions (fig. 5. Two non-uniform meshes were considered: a “fine” mesh with element edge lengths on the boundary of 100μm and 200μm, and a “coarse” mesh with boundary edge lengths 200μm and 400μm. The distributions of element edge lengths (fig. 5) had minimum, average, and maximum edge sizes hmin = 67μm, havg = 119μm, and hmax = 256μm for the fine mesh, and hmin = 130μm, havg = 238μm, and hmax = 516μm for the coarse mesh.
Figure 5.
Figure Comparison of voltage between two non-uniform meshes; finer one with 67μm ≤ x ≤ 256μm and coarser one with 130μm ≤ x ≤ 515μm. The finer nonuniform mesh (D) shows minimal variation in the wavefront compared to the coarser nonuniform mesh (E).
Conduction was initiated by applying a stimilus current of 50, 000μA/cc to the region within 0.15cm of the left boundary. The activation sequence plots (fig. 5) show that by t = 37ms the wave front is still in the uniform mesh region and remains straight and perpendicular to the lateral boundaries. After the wave enters the non-uniform mesh region, by t = 49ms, the wavefront is noticeably curved in the coarser nonuniform mesh. This is a consequence of an artificially slower wavespeed in the upper right partition of the mesh bounded by 400μm element edges. The artifactual curvature of the wave front becomes increasingly pronounced with time, and evident in the snapshots at t = 69ms and t = 100ms. Wave front curvature is barely detectable in the finer nonuniform mesh.
We note that the ratio of largest to smallest element edge length in the present example is less than 5, and completely within the typical range for automated hexahedral and tetrahedral mesh generation procedures that have become common in cardiac modeling [12, 28, 29]. The distortion of the wavefront produced by the larger elements illustrates that the potential for artifactual results is determined more by the largest element size than by the average. Based on the convergence studies in the previous sections, we expect that meshes with elements larger than 200 μm are likely to produce significant errors in conduction. When larger elements are isolated to certain regions, as in the present example, they may cause wavefronts to distort and even change direction, despite a smaller average element size.
4.2. Spiral break
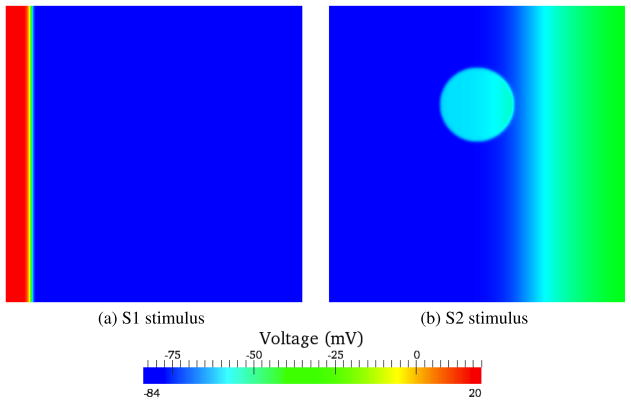
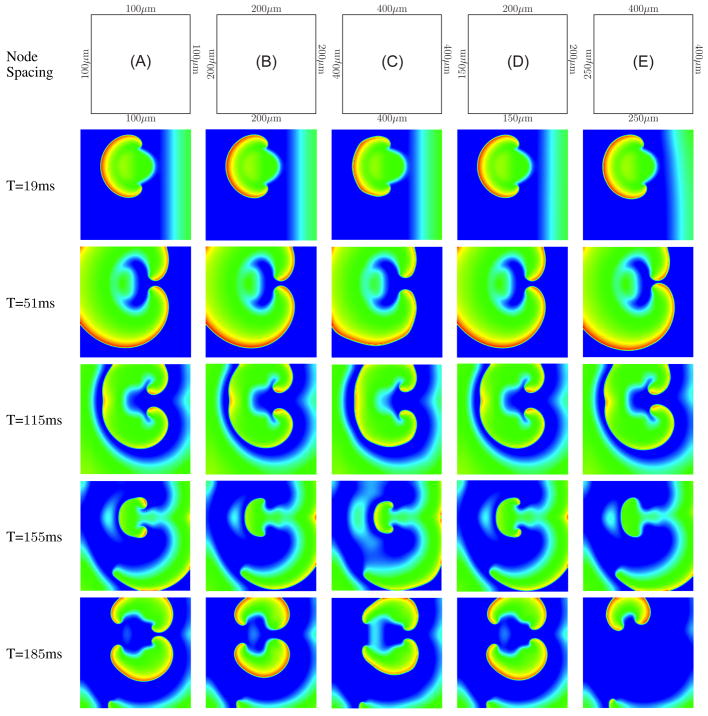
While simplified bar/slab geometries with uniaxial conduction are appropriate for systematic convergence studies, more physiologically relevant simulations commonly involve non-uniform conduction. A particular example is the simulation of spiral/scroll waves associated with cardiac arrhythmia and fibrillation. Here we simulated spiral waves in a 6-cm square block of tissue using a conventional “S1–S2” protocol (fig. 6). The initial stimulus (S1) was applied uniformly along the left edge of the block for 4ms with a stimulus current of 50, 000μA/cc. A second stimulus (S2) was applied after a delay of 265ms subsequent to S1, over a 1-cm radius circular disc offset from the center of the block by 1cm along the Y axis, for 3 ms, also at 50, 000μA/cc. The model was meshed with fully-integrated bilinear quadrilateral elements. The ionic currents were defined using the Luo-Rudy-II ionic model [23]. Five different cases were considered to study the effect of mesh size of producing physiologically acceptable spiral waves (fig. 7): (A) a uniform mesh with 100μm sized elements, (B) a uniform mesh 200μm sized elements, (C) a uniform mesh 400μm sized elements, (D) a nonuniform mesh with two edges set to 150μm and other two set to 200μm sizes elements (hmin = 112μm, havg = 173μm, hmax = 248μm), and (E) a nonuniform mesh with two edges set to 200μm and other two set to 400μm sized elements (hmin = 138μm, havg = 279μm, hmax = 496μm). The uniform 100μm, 200μm and the nonuniform 150 – 200μm show a good agreement in the voltage evolution. However the results from 400μm mesh even at T= 19ms shows a non smooth wavefront. The wavefront exhibits the presence of corners which is physiologically not acceptable. Also the wave front is not smooth, but rather noticeably jagged. A non-smooth wavefront is also obtained from the nonuniform 250 – 400μm mesh, but is not quite as jagged as in the 400μm mesh. Moreover the nonuniform 250 –400μm mesh shows a qualitatively different break up pattern from T= 155ms to T= 185ms: while all the other meshes show two spiral waves, in this mesh the spiral arm in the bottom gets extinguished. This is clearly a artifact of discretization error — the spiral encounters excitable media but nonetheless dies out instead of continuing to propagate. While the extinguishing of spiral waves is physiologically valid, it is not so in the range of phase space corresponding to the specified ionic cell model parameters. This provides an example of how such numerical artifacts could prompt errant physiological conclusions.
Figure 6.
S1 and S2 stimulus locations on the block.
Figure 7.
Comparison of spiral wave breakup between five different meshes. Time shown denotes the time since the application of S2 stimulus. The finer nonuniform mesh shows minimal variation in the wavefront compared to the coarser nonuniform mesh. Uniform mesh (C) and nonuniform mesh (E) show physiologically unacceptable artifacts produced by large element sizes.
5. CONCLUSIONS
In this paper we have examined the combined effects of operator splitting and spatial integration schemes on the accuracy and efficiency of finite-element solution of the reaction-diffusion equations of cardiac electrophysiology. In particular, we have made a break from the standard approach of computing “lumped” approximations to the consistent capacitance and mass matrices that appear in a variational formulation of the boundary value problem. The common argument for “mass lumping” is efficiency — it decouples the nodal equations governing time evolution of voltage, thereby allowing for trivial local time-stepping updates, which are much more CPU-efficient than the solution of coupled linear systems with global (but sparse and banded) matrices. Adding to the observations of others [25], we have shown that this efficiency can sometimes come at a cost of reduced accuracy. However, our convergence studies show that the six distinct choices for preferential lumping can produce a wide range of convergence behaviors. Two schemes in particular — the L-LF scheme and the F-LL scheme — exhibit excellent accuracy in addition to (or despite) increases in efficiency relative to a fully consistent implementation.
In the L-LF scheme, the lumped approximation of capacitance is used in both the diffusion and ionic parts of the operator split, and the consistent (full) ionic mass matrix is used in the ionic update. The lumping of all capacitance matrices in this scheme, which is akin to what Pathmanathan, et al. [25] label “half lumping,” allows for explicit time updates to the voltage to be computed trivially, without the need for solving any global linear system. The multiplication of nodal current densities by a consistent (“full”) mass matrix can be interpreted as producing an additional (artificial) diffusion of ionic currents, which has the effect of speeding up wavefronts, causing the conduction velocity to converge from above as meshes are refined. Despite the speedups afforded with explicit voltage updates, the “full” mass matrix formulation prevents asynchronous, adaptive time-stepping of the ionic part of the operator split, one of the key sources of efficiency afforded by operator splitting. However, the L-LF scheme does allow for global sub-stepping in the ionic solution step. In other words, some efficiency can be gained by doing diffusion updates (Δt) less frequently than ionic updates (Δτ < Δt) while still maintaining comparable accuracy.
In contrast, the F-LL scheme employs a consistent (full) capacitance in the diffusion part of the operator split, and lumped approximations of both the capacitance and mass matrices in the ionic part. Use of the consistent capacitance in the diffusion part can be rationalized a posteriori in light of two considerations. First, with ionic sub-stepping (Δt < Δt) employed, the diffusion part is solved less frequently; thus any reduction in efficiency in a diffusion time step is less consequential than in an ionic time step. But second and more important, because explicit time-stepping of the diffusion part places excessive requirements on the time step Δt, it is generally more efficient, and comparably accurate to use implicit time-stepping for the diffusion updates. Thus, lumping of the capacitance has minimal impact on efficiency of the solution of the linear system for an implicit (e.g., a Crank-Nicholson) diffusion update. In light of this logic, it seems more productive to search for ways of speeding up the ionic part of the operator split. The lumped approximation of both the capacitance and mass matrices in the F-LL scheme does this optimally, by completely decoupling the nodal equations into local ODE’s. As we showed, this result is equivalent to what is achieved either by trading standard Gauss quadrature for nodal quadrature, or by performing the operator split to the original strong form of the BVP, thereby requiring derivation and spatial discretization of the weak form of only the diffusion part of the governing equations. Remarkably, this single modification to the standard “fully lumped” approximation of the operator split equations, using a consistent (full) capacitance matrix only in the diffusion update, allows us to “have our cake and eat it too.” That is, it yields a scheme with accuracy rivaling fully consistent and fully coupled implementations (e.g., ICI and SVI in [9, 25]), but capable of enjoying the tremendous computational speed-ups afforded by asynchronous adaptive time-stepping of the decoupled nodal ionic equations [13].
We examined the accuracy and efficiency of these “preferentially-lumped” operator-split formulations through a sequence of benchmark problems, ranging from simple uniaxial wavefront propagation to spiral wave breakup. We find that results are generally satisfactory for the L-LF and F-LL schemes when element sizes are less than about 200μm. Other lumping combinations require meshes of at least twice the element density for acceptable accuracy. We demonstrated that particular attention to mesh sensitivity must be given when computing with non-uniform meshes, as are the common result of automated segmentation and mesh generation software. Not surprisingly, for nonuniform meshes it is the size of the largest element (and not the smallest or average) that controls the accuracy of the solution and the presence or absence of spurious artifacts. We encountered two key implications of these observations for physiological simulation studies. Local gradients in mesh density, when allowing element sizes to rise above h ≈ 200μm, can cause artifactual changes in the curvature of wavefronts. As demonstrated in the context of re-entry and spiral wave breakup, such errors can lead to predictions that are qualitatively incorrect, e.g., spurious “corner” formation in wave fronts, or even the extinguishing of waves that should continue to propagate. These results underscore the importance of simulating with sufficiently refined meshes.
Acknowledgments
We thank Alan Garfinkel and Zhilin Qu for introducing us to cardiac electrophysiology and for many helpful conversations. We thank Steve Niederer for helpful conversations and for sharing preprints of refs. [22] and [25] with us. We also thank the two referees for helpful critical suggestions. This work was supported in part by a grant from the NIH (P01 HL78931).
A. PERFORMANCE OF LUMPING SCHEMES
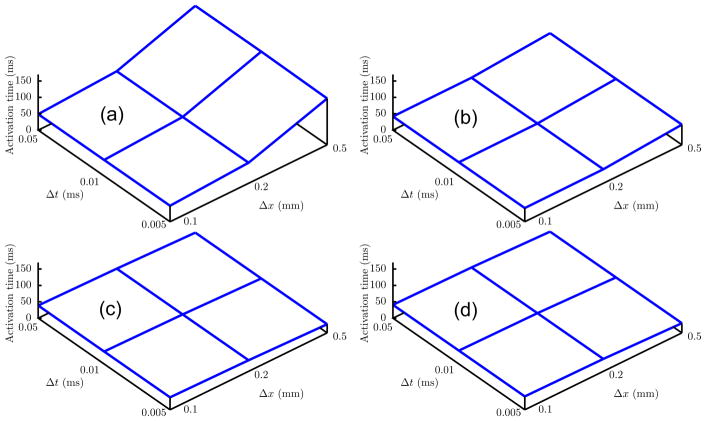
A complete numerical comparison of the activation times for each lumping schemes at each location in the Niederer Benchmark Problem [22] is shown in Table III. For comparison with other codes tested by Niederer et al [22], and to show the impact of changing spatial resolution on activation wave, and propagation along and across the preferential fiber direction, we evaluated activation times in the plane shown first row in Figure 8. Schemes F-LF, F-LL and L-LF show minimal variation compared to L-LL. For the schemes L-LL and F-LL activation time curves have a common morphology, with the activation wave increasing in velocity as the meshes were refined (Figure 9). However schemes F-LF and L-LF exhibit the opposite, the activation wave decreasing in velocity with meshes refined. The change in velocity is less pronounced in F-LL, F-LF and L-LF compared to L-LL.
Figure 8.
For a slice plane connecting points P1 and P8 the activation times comparison between four different schemes show minimal difference in results between different mesh sizes for F-LF and L-LF.
Figure 9.
Activation time at point P8 depicted in Figure 8 for every combination of spatial and temporal refinement. (a) L-LL, (b) F-LL, (c) F-LF and (d) L-LF.
Table III.
Results from solution of Niederer Benchmark Problem [22], using L-LL, F-LL, F-LF, and L-LF variants of the ICI formulation with operator splitting.
| Δx, Δt | P1 | P2 | P3 | P4 | P5 | P6 | P7 | P8 | C |
|---|---|---|---|---|---|---|---|---|---|
| L-LL | |||||||||
| 0.1, 0.005 | 1.46 | 32.68 | 9.56 | 34.69 | 30.68 | 47.62 | 33.49 | 48.68 | 22.67 |
| 0.1, 0.01 | 1.46 | 32.69 | 9.56 | 34.69 | 30.68 | 47.62 | 33.49 | 48.68 | 22.67 |
| 0.1, 0.05 | 1.46 | 32.70 | 9.57 | 34.72 | 30.68 | 47.63 | 33.54 | 48.69 | 22.72 |
| 0.2, 0.005 | 1.46 | 35.86 | 12.57 | 40.69 | 41.65 | 59.66 | 45.63 | 62.67 | 29.75 |
| 0.2, 0.01 | 1.46 | 35.87 | 12.57 | 40.69 | 41.65 | 59.66 | 45.23 | 62.67 | 29.75 |
| 0.2, 0.05 | 1.46 | 35.98 | 12.58 | 40.69 | 41.65 | 59.66 | 45.63 | 62.67 | 29.75 |
| 0.5, 0.005 | 1.46 | 60.30 | 29.61 | 69.95 | 124.34 | 139.62 | 127.63 | 141.62 | 69.49 |
| 0.5, 0.01 | 1.46 | 60.31 | 29.61 | 69.96 | 124.37 | 139.62 | 127.63 | 141.62 | 69.51 |
| 0.5, 0.05 | 1.46 | 59.56 | 29.64 | 69.65 | 125.66 | 141.08 | 129.59 | 142.75 | 66.69 |
| F-LL | |||||||||
| 0.1, 0.005 | 1.46 | 30.77 | 7.72 | 32.55 | 25.63 | 40.68 | 26.71 | 41.66 | 18.98 |
| 0.1, 0.01 | 1.46 | 30.79 | 7.72 | 32.58 | 25.63 | 40.69 | 26.71 | 41.68 | 18.98 |
| 0.1, 0.05 | 1.46 | 31.69 | 7.72 | 32.70 | 25.68 | 40.69 | 26.76 | 41.69 | 19.66 |
| 0.2, 0.005 | 1.46 | 30.69 | 8.71 | 31.70 | 28.68 | 41.97 | 30.68 | 42.77 | 19.90 |
| 0.2, 0.01 | 1.46 | 30.70 | 8.71 | 31.70 | 28.68 | 41.99 | 30.68 | 42.78 | 19.99 |
| 0.2, 0.05 | 1.46 | 30.71 | 8.71 | 31.75 | 28.68 | 42.63 | 30.68 | 43.57 | 19.99 |
| 0.5, 0.005 | 1.46 | 32.66 | 11.64 | 33.83 | 48.60 | 60.99 | 50.62 | 62.13 | 26.79 |
| 0.5, 0.01 | 1.46 | 32.65 | 11.64 | 33.82 | 48.59 | 60.88 | 50.61 | 61.95 | 26.77 |
| 0.5, 0.05 | 1.46 | 32.66 | 11.64 | 33.84 | 48.56 | 60.78 | 50.61 | 61.85 | 26.77 |
| F-LF | |||||||||
| 0.1, 0.005 | 1.46 | 29.91 | 6.75 | 30.74 | 21.91 | 37.57 | 23.59 | 37.73 | 17.83 |
| 0.1, 0.01 | 1.46 | 29.91 | 6.75 | 30.74 | 22.91 | 37.57 | 23.59 | 37.73 | 17.83 |
| 0.1, 0.05 | 1.46 | 30.66 | 6.76 | 31.44 | 22.08 | 37.69 | 23.67 | 37.99 | 17.87 |
| 0.2, 0.005 | 1.46 | 27.78 | 6.68 | 28.71 | 19.86 | 33.71 | 20.74 | 33.74 | 16.69 |
| 0.2, 0.01 | 1.46 | 27.78 | 6.68 | 28.71 | 19.86 | 33.69 | 20.75 | 33.74 | 16.69 |
| 0.2, 0.05 | 1.46 | 28.67 | 6.68 | 28.74 | 19.94 | 33.72 | 20.75 | 34.05 | 16.74 |
| 0.5, 0.005 | 1.46 | 23.82 | 4.70 | 24.45 | 17.16 | 26.00 | 17.57 | 26.47 | 13.41 |
| 0.5, 0.01 | 1.46 | 23.82 | 4.70 | 24.44 | 17.16 | 25.98 | 17.57 | 26.46 | 13.41 |
| 0.5, 0.05 | 1.46 | 23.83 | 4.70 | 24.47 | 17.16 | 26.02 | 17.54 | 26.48 | 13.42 |
| L-LF | |||||||||
| 0.1, 0.005 | 1.46 | 31.31 | 7.69 | 32.62 | 24.65 | 39.74 | 25.69 | 40.70 | 18.98 |
| 0.1, 0.01 | 1.46 | 31.31 | 7.69 | 32.62 | 24.65 | 39.74 | 25.69 | 40.71 | 18.98 |
| 0.1, 0.05 | 1.46 | 31.63 | 7.69 | 32.68 | 24.66 | 40.69 | 25.69 | 40.70 | 19.13 |
| 0.2, 0.005 | 1.46 | 30.64 | 7.51 | 30.94 | 22.78 | 37.43 | 23.72 | 37.72 | 18.58 |
| 0.2, 0.01 | 1.46 | 30.64 | 7.51 | 30.92 | 22.78 | 37.35 | 23.72 | 37.72 | 18.58 |
| 0.2, 0.05 | 1.46 | 30.68 | 7.51 | 31.54 | 22.79 | 37.35 | 23.72 | 37.72 | 18.58 |
| 0.5, 0.005 | 1.46 | 27.55 | 5.48 | 27.65 | 20.06 | 29.57 | 20.52 | 29.65 | 14.83 |
| 0.5, 0.01 | 1.46 | 27.56 | 5.48 | 27.65 | 19.98 | 29.56 | 20.49 | 29.65 | 14.83 |
| 0.5, 0.05 | 1.46 | 27.56 | 5.48 | 27.65 | 19.98 | 29.56 | 20.49 | 29.65 | 14.83 |
Footnotes
These requirements refer to the use of physiologically accurate ionic cell models; phenomenological models such as the FitzHugh-Nagumo model allow for larger spatial/temporal step size [6]. The more realistic ionic models produce spatio-temporal variations at a much broader range of length and time scales, making whole heart modeling all the more challenging.
References
- 1.Keener J, Keener J, Sneyd J. Mathematical physiology: Cellular physiology. 2. Springer Verlag; 2009. [Google Scholar]
- 2.Sundnes J, Lines G, Cai X, Nielsen B, Mardal K, Tveito A. Computing the Electrical Activity in the Heart. Springer-Verlag; 2006. [Google Scholar]
- 3.Lines G, PG, Tveito A. Modeling the electrical activity of the heart: A bidomain model of the ventricles embedded in a torso. Comput Visual Sci. 2003;5:195–213. [Google Scholar]
- 4.Vadakkumpadan F, Rantner L, Tice B, Boyle P, Prassl A, Vigmond E, PG, Trayanova N. Image-based models of cardiac structure with applications in arrhythmia and defibrillation studies. Journal of Electrocardiology. 2009;42:157.e1–157.e10. doi: 10.1016/j.jelectrocard.2008.12.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Bernabeu M, Bishop M, Pitt-Francis J, Gavaghan D, Grau V, Rodriguez B. High performance computer simulations for the study of biological functionin 3d heart models incorporating fibre orientation and realistic geometry atpara-cellular resolution. Computers in Cardiology. 2008;35:721–724. [Google Scholar]
- 6.Goktepe S, Kuhl E. Computational modeling of cardiac electrophysiology: A novel finite element approach. IJNME. 2009;79:156–178. [Google Scholar]
- 7.Göktepe S, Kuhl E. Electromechanics of the heart: a unified approach to the strongly coupled excitation–contraction problem. Computational Mechanics. 2010;45(2):227–243. [Google Scholar]
- 8.Whiteley J. Physiology driven adaptivity for the numerical solution of the bidomain equations. Annals of Biomedical Engineering. 2007;35:1510–1520. doi: 10.1007/s10439-007-9337-3. [DOI] [PubMed] [Google Scholar]
- 9.Pathmanathan P, Mirams G, Southern J, Whiteley J. The significant effect of the choice of ionic current integration method in cardiac electro-physiological simulations. International Journal for Numerical Methods in Biomedical Engineering. 2011;27(11) [Google Scholar]
- 10.Trangenstein J, Kim C. Operator splitting and adaptive mesh refinement for the luo–rudy i model. Journal of Computational Physics. 2004;196(2):645–679. [Google Scholar]
- 11.Cherry EM, Greenside HS, Henriquez CS. A space-time adaptive method for simulating complex cardiac dynamics. Phys Rev Lett. 2000;84(6):1343–1346. doi: 10.1103/PhysRevLett.84.1343. [DOI] [PubMed] [Google Scholar]
- 12.Prassl A, Kickinger F, Ahammer H, Grau V, Schneider J, Hofer E, Vigmond E, Trayanova N, Plank G. Automatically generated, anatomically accurate meshes for cardiac electrophysiology problems. Biomedical Engineering, IEEE Transactions on. 2009;56(5):1318–1330. doi: 10.1109/TBME.2009.2014243. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Qu Z, Garfinkel A. An advanced algorithm for solving partial differential equation in cardiac conduction. IEEE Trans Biomed Eng. 1999;46:1166–1168. doi: 10.1109/10.784149. [DOI] [PubMed] [Google Scholar]
- 14.Sundnes J, Wall S, Osnes H, Thorvaldsen T, McCulloch A. Improved discretisation and linearisation of active tension in strongly coupled cardiac electro-mechanics simulations. Computer Methods in Biomechanics and Biomedical Engineering. 2012 doi: 10.1080/10255842.2012.704368. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Sundnes J, Lines G, Tveito A. Efficient solution of ordinary differential equations modeling electrical activity in cardiac cells. Mathematical Biosciences. 2001;172:55–72. doi: 10.1016/s0025-5564(01)00069-4. [DOI] [PubMed] [Google Scholar]
- 16.Whiteley JP. An Efficient Numerical Technique for the Solution of the Monodomian and Bidomain Equations. IEEE Transactions on Biomedical Engineering. 2006;53(11):2139–2147. doi: 10.1109/TBME.2006.879425. [DOI] [PubMed] [Google Scholar]
- 17.Pathmanathan P, Bernabeu M, Bordas R, Cooper J, Garny A, Pitt-Francis J, Whiteley J, Gavaghan D. A numerical guide to the solution of the bidomain equations of cardiac electrophysiology. Progress in biophysics and molecular biology. 2010;102(2):136–155. doi: 10.1016/j.pbiomolbio.2010.05.006. [DOI] [PubMed] [Google Scholar]
- 18.Austin T, Trew M, Pullan A. Solving the cardiac bidomain equations for discontinuous conductivities. Biomedical Engineering, IEEE Transactions on. 2006;53(7):1265–1272. doi: 10.1109/TBME.2006.873750. [DOI] [PubMed] [Google Scholar]
- 19.Vigmond E, Aguel F, Trayanova N. Computational techniques for solving the bidomain equations in three dimensions. Biomedical Engineering, IEEE Transactions on. 2002;49(11):1260–1269. doi: 10.1109/TBME.2002.804597. [DOI] [PubMed] [Google Scholar]
- 20.Göktepe S, Wong J, Kuhl E. Atrial and ventricular fibrillation: computational simulation of spiral waves in cardiac tissue. Archive of Applied Mechanics. 2010;80(5):569–580. [Google Scholar]
- 21.Bernabeu M, Bordas R, Pathmanathan P, Pitt-Francis J, Cooper J, Garny A, Gavaghan D, Rodriguez B, Southern J, Whiteley J. Chaste: Incorporating a novel multiscale spatial and temporal algorithm into a large scale open source library. Phil Trans Roy Soc (A) 2009 May;367(1895):1907–1930. doi: 10.1098/rsta.2008.0309. [DOI] [PubMed] [Google Scholar]
- 22.Niederer S, Kerfoot E, Benson A, Bernabeu M, Bernus O, Bradley C, Cherry E, Clayton R, Fenton F, Garny A, et al. Verification of cardiac tissue electrophysiology simulators using an n-version benchmark. Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences. 2011;369(1954):4331–4351. doi: 10.1098/rsta.2011.0139. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Luo C, Rudy Y. A dynamic model of the cardiac ventricular action potential. i. simulations of ionic currents and concentration changes. Circ Res. 1994;74:1071–1096. doi: 10.1161/01.res.74.6.1071. [DOI] [PubMed] [Google Scholar]
- 24.Mahajan A, Shiferaw Y, Sato D, Baher A, Olcese R, Xie L, Yang M, Chen P, Restrepo J, Karma A, et al. A rabbit ventricular action potential model replicating cardiac dynamics at rapid heart rates. Biophysical journal. 2008;94(2):392–410. doi: 10.1529/biophysj.106.98160. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Pathmanathan P, Bernabeu M, Niederer S, Gavaghan D, Kay D. Computational modelling of cardiac electrophysiology: explanation of the variability of results from different numerical solvers. International Journal for Numerical Methods in Biomedical Engineering. 2012 doi: 10.1002/cnm.2467. [DOI] [PubMed] [Google Scholar]
- 26.ten Tusscher K, Panfilov A. Alternans and spiral breakup in a human ventricular tissue model. American Journal of Physiology-Heart and Circulatory Physiology. 2006;291(3):H1088–H1100. doi: 10.1152/ajpheart.00109.2006. [DOI] [PubMed] [Google Scholar]
- 27.Heroux MA, Bartlett RA, Howle VE, Hoekstra RJ, Hu JJ, Kolda TG, Lehoucq RB, Long KR, Pawlowski RP, Phipps ET, Salinger AG, Thornquist HK, Tuminaro RS, Willenbring JM, Williams A, Stanley KS. An overview of the trilinos project. ACM Trans Math Softw. 2005;31(3):397–423. [Google Scholar]
- 28.Trayanova NA, Constantino J, Gurev V. Electromechanical models of the ventricles. American Journal of Physiology-Heart and Circulatory Physiology. 2011;301(2):H279–H286. doi: 10.1152/ajpheart.00324.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Vadakkumpadan F, Arevalo H, Prassl AJ, Chen J, Kickinger F, Kohl P, Plank G, Trayanova N. Image-based models of cardiac structure in health and disease. Wiley Interdisciplinary Reviews: Systems Biology and Medicine. 2010;2(4):489–506. doi: 10.1002/wsbm.76. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Xie F, Qu Z, Yang J, Baher A, Weiss J, Garfinkel A, et al. A simulation study of the effects of cardiac anatomy in ventricular fibrillation. Journal of Clinical Investigation. 2004;113(5):686–693. doi: 10.1172/JCI17341. [DOI] [PMC free article] [PubMed] [Google Scholar]