| 1: INPUTS:
|
The learnt mean atlases 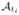
|
| The learnt cloud C
|
| The baseline ground truth shape S0
|
2: Initialize Svirtual ←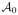 0. 0. |
3: Initialize S̃i ←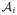 i for i ∈ {1, . . . , N} i for i ∈ {1, . . . , N} |
4: Initialize ε as the mean distance between S0 and 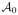 0 plus its standard deviation 0 plus its standard deviation |
| 5: for every vertex x in the virtual shape Svirtual that is located outside the ε–neighborhood from S0
do
|
| Update its position using the closeness metric (1 or 2) |
| Retrieve (or update if using Metric 2) its dynamic feature (evolution trajectory) c(x, t)t∈[0,T]
|
|
|
| 6: end for
|
| 7: Estimate the geodesic current-based baseline shape evolution using {S0, {S̃i}} by minimizing:
|
| 8: OUTPUT:
|
| Set of predicted surfaces { S̃i} at timepoints ti with i ∈ {0, . . . , N} |
| Set of smooth temporal evolution trajectories for vertices in S0 for t ∈ [0, tN] |
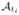
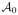 0.
0.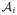 i for i ∈ {1, . . . , N}
i for i ∈ {1, . . . , N}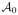 0 plus its standard deviation
0 plus its standard deviation