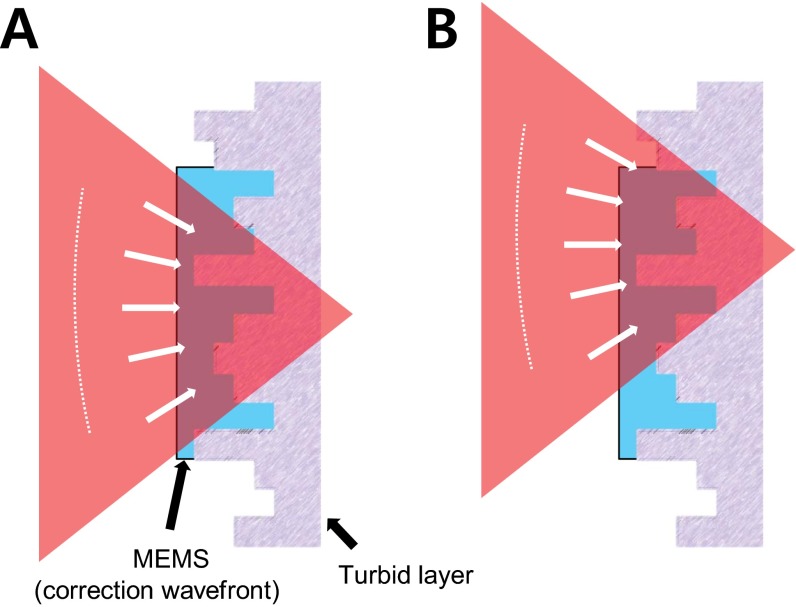
Fig. S1.

Beam scanning in the turbid layer-conjugation geometry. (A) The beam is parked at a target location. The schematic illustrates the turbid layer as a thin random phase plate, where the MEMS compensates the phase distortions after the wavefront measurement. Through this window, the aberrations are compensated efficiently and the impinging spherical wave on the MEMS passes through the turbid layer, resulting in a diffraction-limited focus at the target position. (B) As the MEMS is conjugated to the turbid layer, the correction pattern is stationary while the beam is scanned. For an infinitely thin turbid layer, the correction would still be perfect and the correction efficiency will only drop as a function of the area that shifts to the outside of the correction pattern. In reality, biological tissues have finite thickness, and therefore the infinitely thin turbid-layer assumption is inaccurate. Comparing A and B, we can find that the beam incident on the individual pixels of the MEMS changes incident angle because of the translation of the spherical wavefront. Therefore, the wavefront correction is no longer perfect, leading to a reduced Strehl ratio.