Significance
Predicting the onset of transitions in the qualitative dynamics of complex systems remains a challenging problem, with relevance in diverse fields. This study focuses on the development of early warning signals that can predict the onset of alternating cardiac rhythms. We treat cardiac cells with a potassium channel blocker, which induces the initiation of alternating rhythms. Based on these experiments, we develop a quantitative measure that can detect how far the system is from the transition. Our results suggest that it is possible to predict the onset of potentially dangerous alternating rhythms in the heart.
Keywords: early warning signals, period-doubling bifurcations, cardiac arrhythmias, dynamical systems
Abstract
Biological, physical, and social systems often display qualitative changes in dynamics. Developing early warning signals to predict the onset of these transitions is an important goal. The current work is motivated by transitions of cardiac rhythms, where the appearance of alternating features in the timing of cardiac events is often a precursor to the initiation of serious cardiac arrhythmias. We treat embryonic chick cardiac cells with a potassium channel blocker, which leads to the initiation of alternating rhythms. We associate this transition with a mathematical instability, called a period-doubling bifurcation, in a model of the cardiac cells. Period-doubling bifurcations have been linked to the onset of abnormal alternating cardiac rhythms, which have been implicated in cardiac arrhythmias such as T-wave alternans and various tachycardias. Theory predicts that in the neighborhood of the transition, the system’s dynamics slow down, leading to noise amplification and the manifestation of oscillations in the autocorrelation function. Examining the aggregates’ interbeat intervals, we observe the oscillations in the autocorrelation function and noise amplification preceding the bifurcation. We analyze plots—termed return maps—that relate the current interbeat interval with the following interbeat interval. Based on these plots, we develop a quantitative measure using the slope of the return map to assess how close the system is to the bifurcation. Furthermore, the slope of the return map and the lag-1 autocorrelation coefficient are equal. Our results suggest that the slope and the lag-1 autocorrelation coefficient represent quantitative measures to predict the onset of abnormal alternating cardiac rhythms.
The development of early warning signals to predict the onset of transitions in complex systems is relevant in diverse contexts (1), including climate change (2, 3), ecology (4, 5), population dynamics (6–8), physiology (9, 10), and finance (11). Anticipating the onset of these transitions remains challenging. From a mathematical perspective, these transitions are related to bifurcations, whereby a change in the value of a model parameter leads to qualitative differences in the dynamics of the system. For a number of bifurcations, as a parameter value approaches a bifurcation point, there is a slower return to equilibrium following a perturbation. Recent studies have developed early warning signals based on this property (1, 2, 4, 5, 6, 8, 12). Most of this work has been based on small amounts of data; the development of statistical indicators based on larger data sets is of considerable importance.
Transitions in the qualitative dynamics of complex systems can be classified into two categories: noise-induced transitions and noisy bifurcations (13). Noise-induced transitions take place when the system’s intrinsic noise leads to a change in the dynamics. Predicting the onset of noise-induced transitions is difficult because the underlying properties of the system have not changed, but rather a chance event (typically a large excursion from the steady-state value) leads to a transition in the dynamics (3, 13). Noisy bifurcations take place when the value of a parameter goes through a bifurcation point, giving rise to a new dynamic. Because the system’s dynamics can change in the neighborhood of bifurcations, it is possible to develop early warning signals that anticipate the transition (12). However, the parameter responsible for the transition in dynamics must be slowly varying, a restriction on the effectiveness of these early warning signals (14, 15).
Recent work on early warning signals has focused on developing indicators to predict the onset of critical transitions that take place through fold bifurcations, where, at a critical parameter value, the system transitions from one stable steady-state value to another (1). Although there may be practical difficulties (13, 16), increases in the system’s variability and autocorrelation can sometimes predict the onset of these transitions. Another phenomenon that can precede a fold bifurcation is flickering, where the system flips back and forth between two stable steady states near a critical parameter value (17). However, transitions in physical, chemical, and biological systems take place through a number of bifurcations with varying properties near the onset of these different bifurcations (18).
In the human heart, a number of mechanisms underlie the transition from normal cardiac rhythm to arrhythmia. The onset of an alternating cardiac rhythm, where, for example, an alternation in the duration of the action potential is observed, represents one such mechanism (19, 20). These alternating rhythms can herald the initiation of arrhythmias, including tachycardia and fibrillation (20−22). T-wave alternans is an arrhythmia for which an alternation in the T wave of the electrocardiogram is observed. Clinically, the manifestation of T-wave alternans increases the patient’s risk of sudden cardiac death (23, 24).
The mechanism underlying the transition from normal cardiac rhythm to an alternating rhythm is linked to a mathematical instability called a period-doubling bifurcation, where the period of the system’s oscillation doubles as a consequence of a change in the value of a model parameter (25–27). Examples of parameters that can induce a period-doubling bifurcation in cardiac systems include pacing frequency (28), temperature (29), and drugs (30, 31). Thus, further development of statistical measures to predict the onset of period-doubling bifurcations is clinically relevant. Theoretical studies have demonstrated that, near the onset of the period-doubling bifurcation, dynamical slowing down takes place, giving rise to noisy precursors such as the emergence of an additional peak in the power spectrum (32, 33).
In two previous studies, we presented experimental data where we treated spontaneously beating aggregates of embryonic chick cardiac cells with E4031, a potassium channel blocker (31, 34). Drug treatment led to the initiation of complex dynamics, including alternating rhythms, bursting rhythms, accelerated rhythms, and chaotic dynamics. We modeled and analyzed these rhythms using numerical simulations and 1D maps (31, 34). Drug treatment also led to the onset of period-doubling bifurcations. Here, we analyze these period-doubling bifurcations to develop early warning signals of these transitions in dynamics.
Analyzing the interbeat intervals, we show that, near the onset of the period-doubling bifurcation, the system’s variability increases and oscillations appear in the autocorrelation function (ACF), observations consistent with theoretical predictions. Analysis of return maps composed of interbeat intervals—for which the current interbeat interval is plotted as a function of the following interbeat interval—reveals that the linear slope of the return map represents a quantitative measure that can assess how close the system is to a period-doubling bifurcation. This work demonstrates the presence of early warning signals for transitions in noisy cardiac systems.
Results
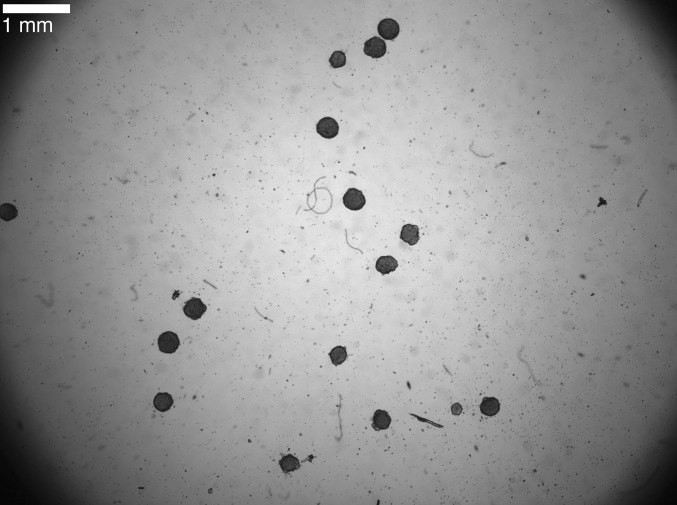
We treated spontaneously beating aggregates of 7-d-old embryonic chick cardiac cells with 0.5–2.5 μmol E4031, a drug that blocks the human Ether-à-go-go-Related Gene (hERG) potassium channel (35, 36). The ovoid-shaped aggregates, with diameters between 100 μm and 300 μm, beat spontaneously with intrinsic periods between 1 s and 2 s. We monitored the activity of the spontaneously beating aggregates by measuring the variation in light intensity of a pixel on the edge of each aggregate. Estimates of the magnitude of the displacement of the aggregate as a consequence of the beat (or contraction) are on the order of ∼5 μm, which is consistent with previous measurements (37). We analyzed the beat dynamics of the aggregates by computing interbeat intervals, the time between successive beats. Furthermore, the beat dynamics of multiple aggregates can be tracked in parallel; Fig. S1 displays an image of a representative experiment. See Materials and Methods for a full description of the protocol used to generate the aggregates and for further details related to how we imaged the aggregates’ beat dynamics.
Fig. S1.
Spontaneously beating aggregates of 7-d-old embryonic chick cardiac cells following treatment with 1.7 μm E4031. The aggregates are the dark, ovoid-shaped regions located on the dish. The aggregates have an average size of 289 μm ± 29 μm. Imaging of several aggregates took place in parallel. The imaging takes place within a 1 cm2 field of view, and the beat dynamics are recorded by monitoring the changes in light intensity from a pixel on the edge of each of the aggregates.
Following drug treatment, the aggregates maintain their intrinsic beat frequency for roughly 10–55 min before a transition in the dynamics takes place. In one of the previous papers from our group based on this data set (34), Kim et al. proposed—using a spatially extended ionic model of the spontaneously beating aggregate—that diffusion of the drug within the aggregate represented a possible mechanism underlying the time dependence of the transitions in dynamics. These transitions in qualitative dynamics lead to a spectrum of complex rhythms. Here, we focus on 23 aggregates for which we observe and capture period-doubling bifurcations.
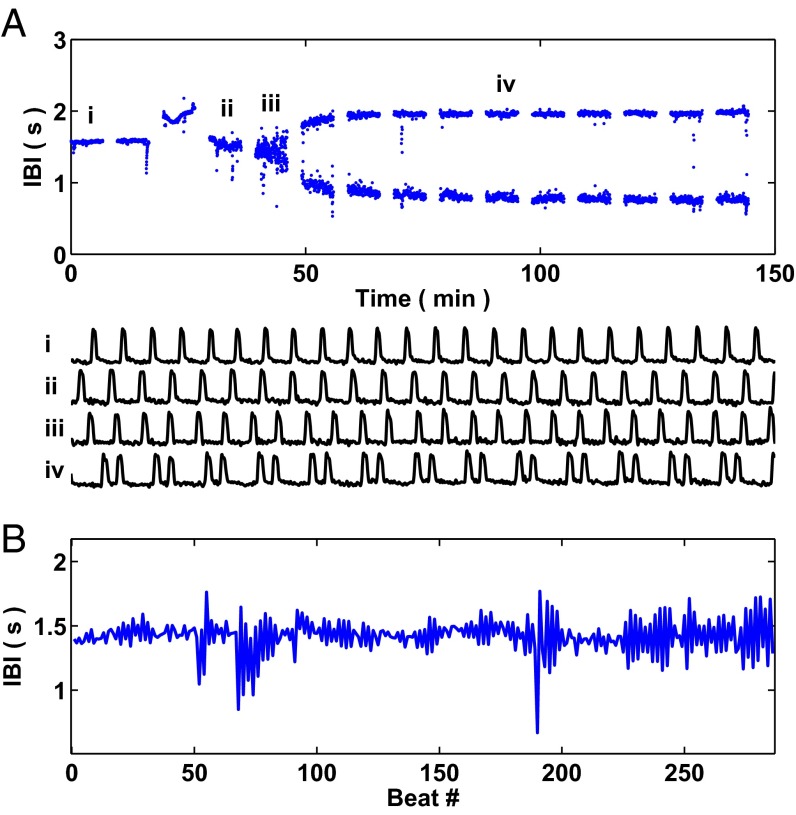
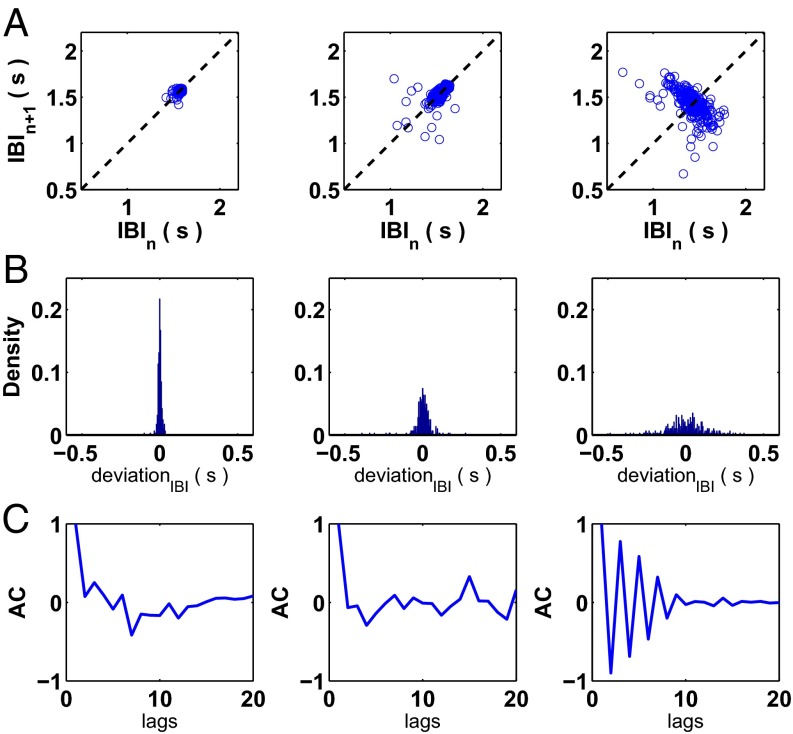
Fig. 1A displays the interbeat intervals from a representative aggregate for which a period-doubling bifurcation takes place following the treatment with 1.5 μmol E4031 at t = 0. The spaces between the sets of interbeat intervals in Fig. 1A represent the times when recording was stopped for data storage purposes (2−3 min). The four representative time series plotted in Fig. 1A correspond with the dynamics in the first (trace i), fourth (trace ii), fifth (trace iii), and tenth (trace iv) sets of interbeat intervals. In mathematics, a period-doubling bifurcation occurs when the slope at the fixed point of a 1D map passes through −1. In this study, we define a period-doubling bifurcation to have taken place when the slope of a linear regression of a return map composed of a sliding window of interbeat intervals is below −0.98 for five consecutive beats—see Materials and Methods for details related to the computation of the slope from the interbeat intervals. Using the above definition, the period-doubling bifurcation takes place near the end of the fifth set of interbeat intervals at approximately t = 45 min in Fig. 1A. (There are other methods to identify the precise timing of period-doubling bifurcations, including identifying the time at which a sliding window of values gives rise to a bimodal distribution.)
Fig. 1.
Period-doubling bifurcation in an aggregate of embryonic chick cardiac cells following treatment with a potassium channel blocker. (A) Interbeat intervals (IBI) through time following treatment with E4031, a potassium channel blocker, at t = 0. There are spaces between segments of the interbeat intervals (2–3 min in duration) for data storage reasons. A period-doubling bifurcation takes place at approximately t = 45 min. The traces below the interbeat intervals—i, ii, iii, and iv—represent time series corresponding with the interbeat intervals in the first, fourth, fifth, and tenth sets of interbeat intervals. Each trace is 37.5 s in duration. (B) A blown-up picture of the fifth set of interbeat intervals (from approximately t = 42 min to t = 48 min) corresponding with trace iii in A.
In the neighborhood of a period-doubling bifurcation, the system takes longer to recover to equilibrium following a perturbation (32, 33). Hence, the system reestablishes the steady-state value less rapidly (and in an oscillatory fashion) leading to negative correlation between successive beats, which we observe in Fig. 1B—a zoomed-in plot of the fifth set of interbeat intervals from Fig. 1A (corresponding with the time series displayed in trace iii).
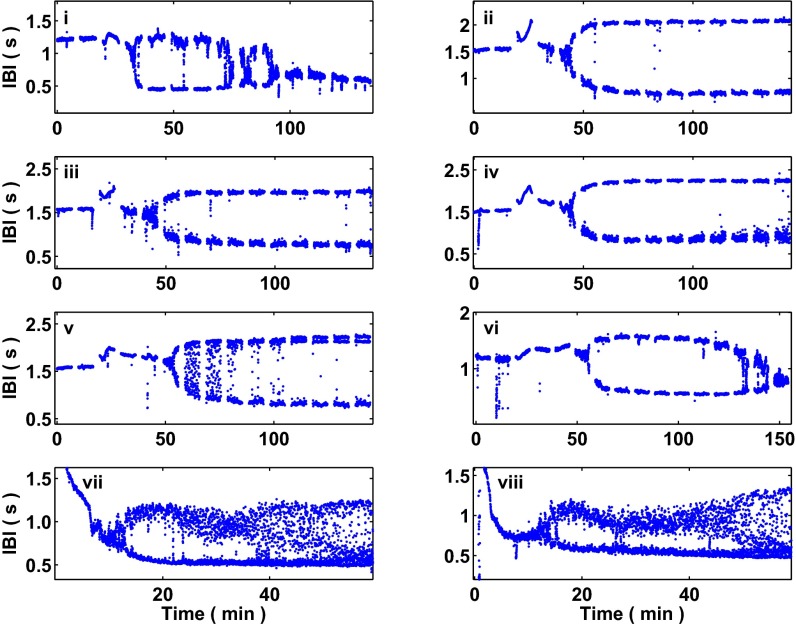
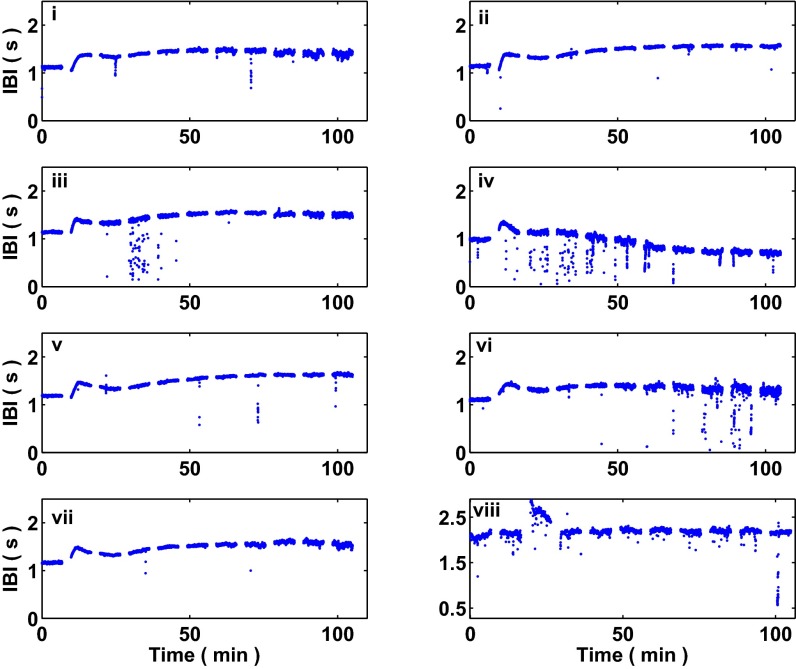
Of the aggregates we analyzed, 43 out of 104 underwent period-doubling bifurcations. Fig. S2 displays raw interbeat interval data from eight aggregates for which we observe and capture period-doubling bifurcations following treatment with E4031. (See SI Text for more details related to the observations of period-doubling bifurcations in the aggregates following drug treatment.) In 71 out of 104 cases, the aggregates exhibited an alternating rhythm. In 19 out of 104 cases, the aggregates’ interbeat intervals simply decreased, establishing a stable, accelerated rhythm. In 14 out of 104 cases, the aggregates’ dynamics did not undergo a qualitative transition in dynamics, maintaining their intrinsic beat frequency for the duration of the experiment; Fig. S3 displays raw interbeat interval data from eight aggregates for which a dynamic transition did not take place. Due to the long time course of the experiments, aggregates could undergo multiple transitions in dynamics throughout the course of a single experiment. In Fig. S2, aggregate i, a period-doubling bifurcation takes place at roughly t = 40 min, leading to the onset of an alternating rhythm; then, at approximately t = 100 min, an additional transition takes place, leading to the establishment of a stable, accelerated rhythm.
Fig. S2.
Interbeat intervals computed from spontaneously beating aggregates that undergo period-doubling bifurcations following treatment with E4031, a potassium channel blocker. Shown are the beat dynamics from eight spontaneously beating aggregates that undergo period-doubling bifurcations. Aggregates i–vi have stops in the recording (each stop is roughly 2–3 min in duration), and aggregates vii and viii are continuously recorded. The timing of the onset of the period-doubling bifurcation ranges from roughly 10 min to 55 min. The slope measure and the lag-1 autocorrelation coefficient in the neighborhood of the period-doubling bifurcation from these aggregates are analyzed in Fig. 4.
Fig. S3.
Interbeat intervals computed from spontaneously beating aggregates that do not undergo a transition in qualitative dynamics following treatment with E4031. Shown are the beat dynamics from eight spontaneously beating aggregates that do not undergo period-doubling bifurcations. These aggregates maintain their intrinsic beat frequency throughout the duration of the experiment. Analysis of these aggregates—as well as additional examples—are used to compute the false positive rate of the slope measure in Fig. S6.
To quantify how the statistical features of the interbeat intervals change as the system approaches the period-doubling bifurcation, we examine the system’s noise and autocorrelation. In Fig. 2A, we plot the return maps for the first (trace i), fourth (trace ii), and fifth (trace iii) sets of interbeat intervals from Fig. 1A. As the system approaches the period-doubling bifurcation, the variation of the interbeat intervals increases and successive interbeat intervals become negatively correlated. In Fig. 2B, we plot the histograms of the detrended interbeat intervals (see Materials and Methods for details on detrending) again for the same sets of interbeat intervals examined above in Fig. 1A. The distributions of interbeat intervals spread out, suggesting an amplification of the noise.
Fig. 2.
Detection of noise amplification and oscillations in the ACF of the aggregate’s interbeat intervals in the neighborhood of the period-doubling bifurcation following treatment with potassium channel blocker. (A) Return maps of the interbeat intervals from the first (trace i), fourth (trace ii), and fifth (trace iii) sets of interbeat intervals from Fig. 1A. (B) Histograms of 250 detrended interbeat intervals for the three sets of interbeat intervals (traces i, ii, and iii) from Fig. 1A. Deviation represents the deviation of each interbeat interval from the mean value computed through the detrending process. The noise amplifies as the system approaches the period-doubling bifurcation. (C) Autocorrelation function (ACF) for a window of 20 detrended beats centered on the 150th beat for three sets of interbeat intervals. Damped oscillations emerge in the ACF in trace iii, consistent with the oscillations in the interbeat intervals observed in Fig. 1B.
In Fig. 2C, we compute the ACF for a set of detrended interbeat intervals (20 beats long) centered at the 150th beat for the same three sets of interbeat intervals we looked at above. Near the beginning of the experiment (), because the system is far from the bifurcation, successive interbeat intervals are uncorrelated, so the lag-1 autocorrelation coefficient is approximately equal to zero, as shown in the ACFs computed for trace i (Fig. 2C, Left) and trace ii (Fig. 2C, Middle) in Fig. 2C. However, as the system nears the bifurcation, damped oscillations emerge in the ACF, reflecting the effect of longer recovery times following perturbations in the neighborhood of the bifurcation, as shown in Fig. 2C, Right. Noise amplification and oscillations in the autocorrelation represent early warning signals to anticipate the onset of period-doubling bifurcations.
In a previous study (31), we modeled the interbeat intervals observed in the experimental data following the treatment with E4031 using an exponential nonlinear 1D map in the absence of noise. To analyze the early warning signals, we continuously perturb an exponential nonlinear map as follows:
| [1] |
where represents the nth interbeat interval and is a random variable drawn from a normal distribution with a mean equal to zero and an SD (σ) equal to 0.01, consistent with the fluctuations observed in the interbeat intervals when the system is far from the bifurcation. The parameters and δ govern the shape of the exponential map. To simulate the experiments, we study the dynamics of the map as we decrease γ. The map has a unique fixed point, which, at a critical γ, destabilizes, giving rise to a period-doubling bifurcation. (See Materials and Methods for a description of the numerical simulations and parameter values.)
To derive analytic expressions for both the probability density function (PDF) and the ACF as the system approaches a period-doubling bifurcation, we approximate the dynamics of Eq. 1 using a continuously perturbed linear 1D map, examining the dynamical features as the slope at the fixed point ( 0) approaches −1. We define the noisy linear map,
| [2] |
where represents the deviation of the nth interbeat interval from the mean and is a random variable drawn from a normal distribution with a mean of zero and an SD (σ) equal to 0.01, consistent with the system-level noise of the experimental data. A represents the slope of the map at the fixed point, . The analytic expressions for the PDF and the ACF of a noisy linear map are well known (1, 38, 39). Iterating the map directly leads to the following series: , which gives the PDF as (1, 38),
| [3] |
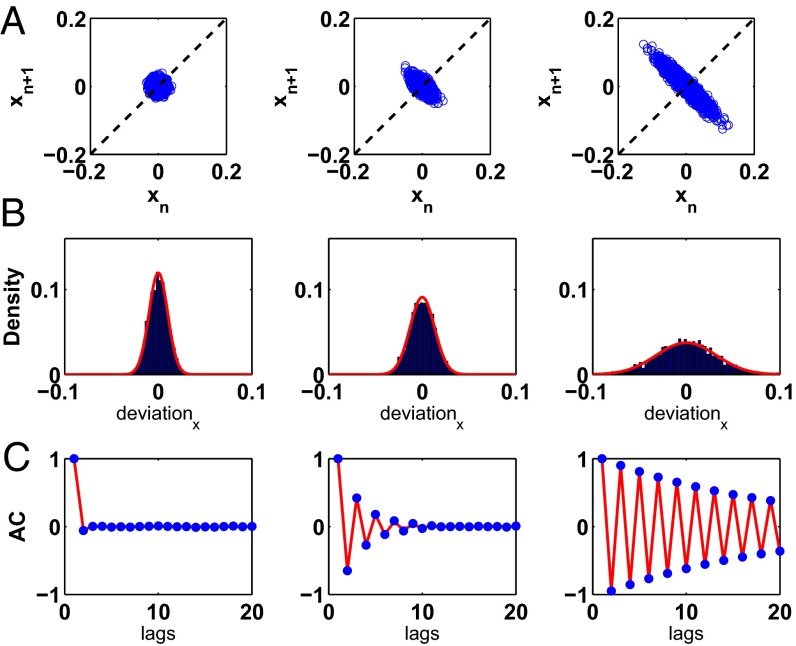
The SD of the PDF is and grows nonlinearly as A approaches −1. Fig. S4A shows return maps for Eq. 2 for three values of A: −0.05, −0.65, and −0.95. In Fig. S4B, we superimpose the analytic expressions for the PDFs as defined by Eq. 3 for the three values of A upon histograms of data generated by Eq. 2; the numerical simulations and the analytical expression are in close agreement. The analytic expression for the ACF of a noisy linear map is also well known (39),
| [4] |
where represents the ACF at lag k. For 0, we observe damped oscillations in the ACF as a function of k. Additionally, as A approaches −1, the ACF decays to zero (no correlation) less rapidly and the oscillations in the ACF grow in amplitude, properties consistent with experiments. In Fig. S4C, we show that the numerically computed ACF and the analytical expression for the autocorrelation, Eq. 4, show close agreement.
Fig. S4.
Detection of noise amplification and oscillations in the ACF as the slope at the fixed point of a continuously perturbed linear map approaches −1. (A) Representative return maps for three values of slope A (the slope at the fixed point): −0.05 (Left), −0.65 (Middle), and −0.95 (Right). For these simulations, we applied normally distributed noise with an SD 0.01. (B) Histograms of the deviation from the mean for the last 4,000 values of x (as shown above in the return maps) for the three values of slope A. The red curves represent the PDFs computed using Eq. 4. (C) ACFs for the three above values of slope A. The blue dots represent the numerically computed ACF, and the red curve represents the analytical expression for the ACF calculated using Eq. 4.
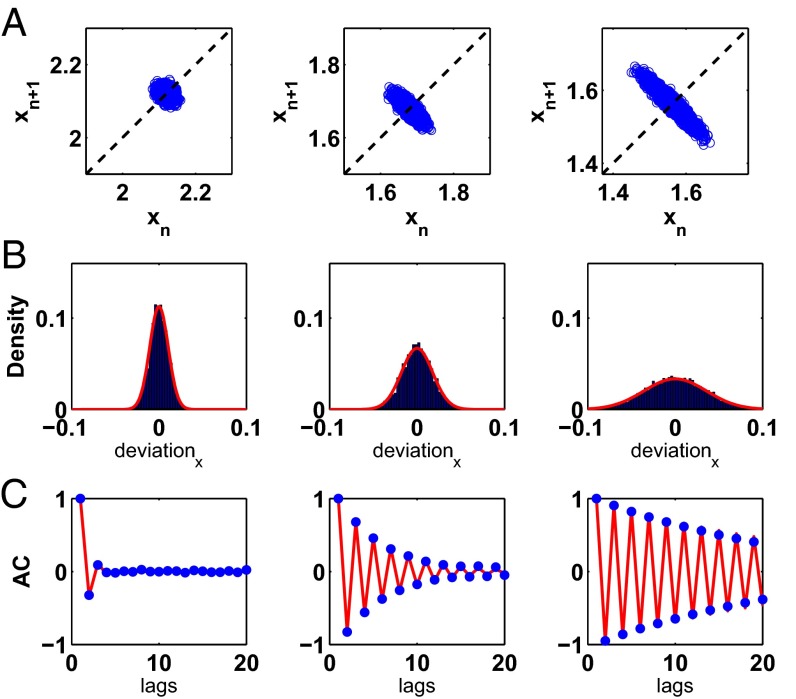
Fig. 3A shows the return maps computed from Eq. 1, the nonlinear map, for three values of γ: 3.0, 1.75, and 1.5. Consistent with the return maps displayed in Fig. 2A, as γ decreases, the slope through the fixed point approaches −1, leading to noise amplification and negative correlation between successive beats. Fig. 3 B and C show that the analytic expressions for the PDF and the ACF—where A represents the linear slope at the fixed point—capture the noise amplification and the oscillations in the ACF as the system approaches the period-doubling bifurcation.
Fig. 3.
Detection of noise amplification and oscillations in the ACF for a model of the data in the neighborhood of a period-doubling bifurcation. (A) Return maps computed from Eq. 1 for 3.0 (Left), 1.75 (Middle), and 1.5 (Right). (B) Histograms and PDFs corresponding to the data that make up the return maps. Deviation represents the deviation of each x value from the mean value of the sequence of x values. The red curve represents the analytic expression of the PDF computed from the linear approximation, Eq. 3. (C) The blue dots represent the ACF determined numerically, and the red curve represents the analytic expression computed from the linear approximation, Eq. 4, for all three values of γ.
As stated earlier, period-doubling bifurcations in 1D maps take place when the slope through the fixed point of a control function goes through −1. Thus, the slope of a linear regression of a return map composed of a sliding window of detrended interbeat intervals computed directly from the experimental data represents a quantitative measure to assess how close the system is to a period-doubling bifurcation.
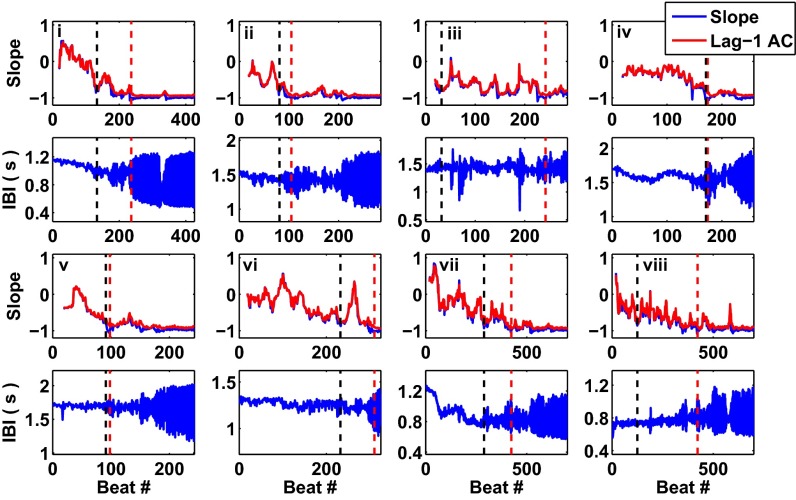
We compute the slope measure from the interbeat intervals taken from the 23 aggregates for which we observe and capture period-doubling bifurcations. In Fig. 4, each slope trace is computed based on the interbeat interval trace given in the panel below. Eq. 4 predicts that the lag-1 autocorrelation coefficient should be equal to the slope through the fixed point, A, of a 1D map: . Hence, we plot the lag-1 autocorrelation coefficient in Fig. 4, showing that the slope and the lag-1 coefficient are consistent.
Fig. 4.
Slope of a return map and the lag-1 autocorrelation coefficient represent quantitative measures that assess how far the aggregates’ dynamics are from a period-doubling bifurcation. (Traces i–viii) Each panel is a representative example of an aggregate for which we observed and captured a period-doubling bifurcation in the dynamics of the interbeat intervals. Each panel displaying the slope measure (Upper) is based on the interbeat interval trace given below it (Lower). The slope (in blue) represents the slope of a linear regression of a return map composed of a sliding window of the previous 20 detrended interbeat intervals. The lag-1 autocorrelation coefficient of the same sliding window of detrended interbeat intervals (in red) is consistent with the slope measure. The black hatched line represents the time at which the slope measure goes below −0.75 for five consecutive beats, which we consider the early warning signal threshold. The red hatched line represents the beat at which the slope first goes below −0.98 for at least five consecutive beats, which we consider the time at which the system goes through the period-doubling bifurcation.
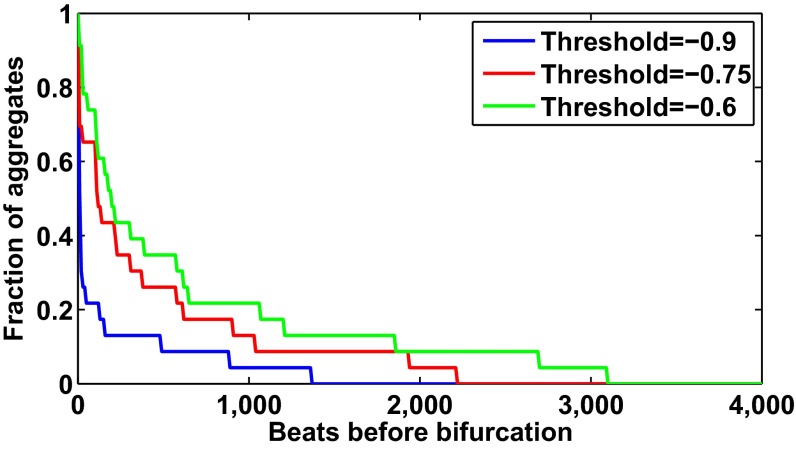
The red hatched lines in Fig. 4 represent the time at which the system undergoes a period-doubling bifurcation. When the slope goes below −0.75 for at least five consecutive beats—the early warning signal threshold, given by the black hatched line in Fig. 4—the period-doubling bifurcation takes place between 1 and 2,231 beats later. Survival analysis using Kaplan–Meier curves performed for three values of threshold—−0.9, −0.75, and −0.6—shows that −0.75 provides considerably more early warning than −0.9 (see Fig. S5 and SI Text for a full explanation of the methods for the survival analysis). For an early warning threshold of −0.9, half of the aggregates had gone through the threshold within 11 beats before the transition; in contrast, for a threshold of −0.75, half of the aggregates had gone through the threshold within 115 beats before the transition.
Fig. S5.
Predictor quality depends on early warning threshold. Using 23 aggregates that undergo period-doubling bifurcations, we computed estimates of the fraction of aggregates that had gone through the early warning signal threshold as a function of beats before the bifurcation for three threshold values: −0.9 (blue), −0.75 (red), and −0.6 (green); 50% of the aggregates had gone through the threshold 11, 115, and 195 beats before the bifurcation for thresholds −0.9, −0.75, and −0.6, respectively.
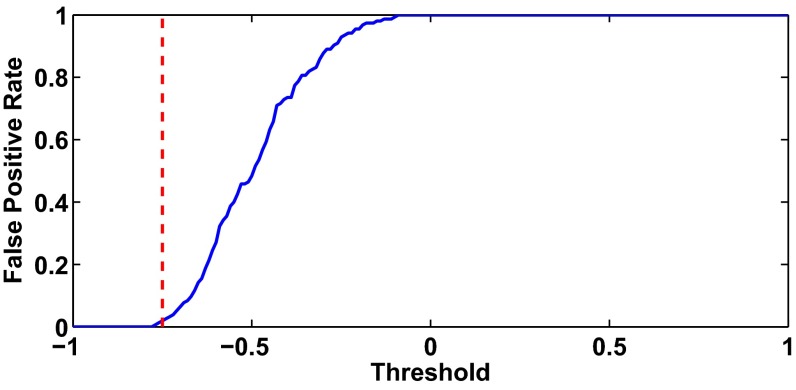
To evaluate how the false positive rate changes as a function of the early warning signal threshold, we analyze data collected from aggregates—n 14, totaling ∼17.5 h of recording—for which a qualitative change in dynamics does not take place. Due to the stops in the recording, we divide the data from the 14 aggregates into 155 segments (1 segment 409.6 s), and thus consider a false positive to have taken place if the slope measure goes below the given threshold for five consecutive beats at least once in a given segment. For an early warning threshold of −0.75, the false positive rate is 0.02, meaning there were 3 time segments (out of 155) for which we observed a false positive. Hence, an early warning threshold of −0.75 represents a balance between maximizing the amount of early warning and minimizing the number of false positives. See Fig. S6 and SI Text for a full explanation of how we computed the false positive rate.
Fig. S6.
False positive rate as a function of early warning signal threshold. Using data from 14 aggregates for which a transition in the qualitative dynamics did not take place following E4031 treatment, we computed the false positive rate as a function of early warning signal threshold. The red hatched line represents the early warning signal threshold equal to −0.75. See Fig. S6: False Positive Rate for a full description of the methods.
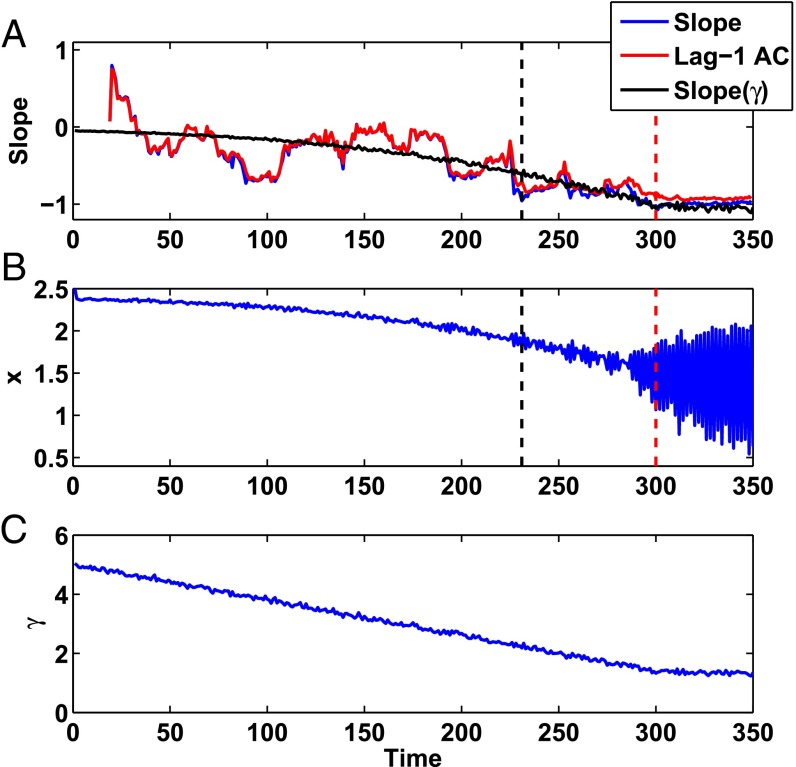
We simulated the period-doubling bifurcation using Eq. 1 by linearly decreasing the value of γ (see Materials and Methods for further details and parameter values). To mimic the experiments, we applied both parametric noise to γ and system-level noise as given in Eq. 1. In Fig. 5A, we compute the slope measure, the lag-1 autocorrelation coefficient, and the value of the slope at the fixed point given by Eq. 1 as a function of γ. Consistent with the experiments, all three measures approach −1 as the system nears the period-doubling bifurcation. The black dashed line represents the early warning signal, and the red dashed line represents the period-doubling bifurcation, with the same criteria given above—the early warning signal predicts the onset of the bifurcation 69 beats in advance. Fig. 5B gives the values of x for the system with the corresponding values of γ given below in Fig. 5C.
Fig. 5.
Slope of a return map and the lag-1 autocorrelation coefficient represent quantitative measures that assess how far the nonlinear map (Eq. 1) is from the period-doubling bifurcation. (A) The slope measure (in blue) represents the slope of a linear regression through a return map composed of a sliding window of the previous 20 detrended values of x (as given in B). The lag-1 autocorrelation coefficient of a sliding window composed of the previous 20 detrended values of x (in red) is consistent with the slope of the linear regression of the return map. Slope(γ) represents the slope of the fixed point as calculated using Eq. 1 and the current value of γ as given in C. The black dashed line represents the early warning, and the red hatched line represents the period-doubling bifurcation. (B) The value of x as numerically generated by Eq. 1 as a function of time. (C) The value of γ as a function of time.
Discussion
In order for early warning signals to be practically useful, they should provide quantitative information to make predictions (40, 41). When the slope of a linear regression of a sliding window of detrended interbeat intervals (also equal to the lag-1 autocorrelation coefficient) reaches −1, the system undergoes a period-doubling bifurcation. Thus, the slope and lag-1 autocorrelation coefficient represent quantitative early warning signals that can detect oncoming period-doubling bifurcations.
As the system nears the period-doubling bifurcation, the slope and lag-1 autocorrelation coefficient approach −1 at different rates (Fig. 4). To account for this diversity, in Fig. 5, we apply system-level noise, parametric noise, and the dynamic influence of slowing down to a 1D map undergoing a period-doubling bifurcation. The interactions of all these dynamic features gives rise to the complex slope and lag-1 autocorrelation coefficient trajectories as the system approaches the bifurcation, consistent with experiments.
Period-doubling bifurcations take place in higher-dimensional models that simulate cardiac systems. In Fig. S7, we analyze a continuously perturbed 2D map of action potential duration in the neighborhood of a period-doubling bifurcation, and observe noise amplification and oscillations in the ACF, consistent with the early warning signals observed and presented for the continuously perturbed 1D map (1, 42). Further details related to the 2D map and the analysis of the model are provided in SI Text.
Fig. S7.
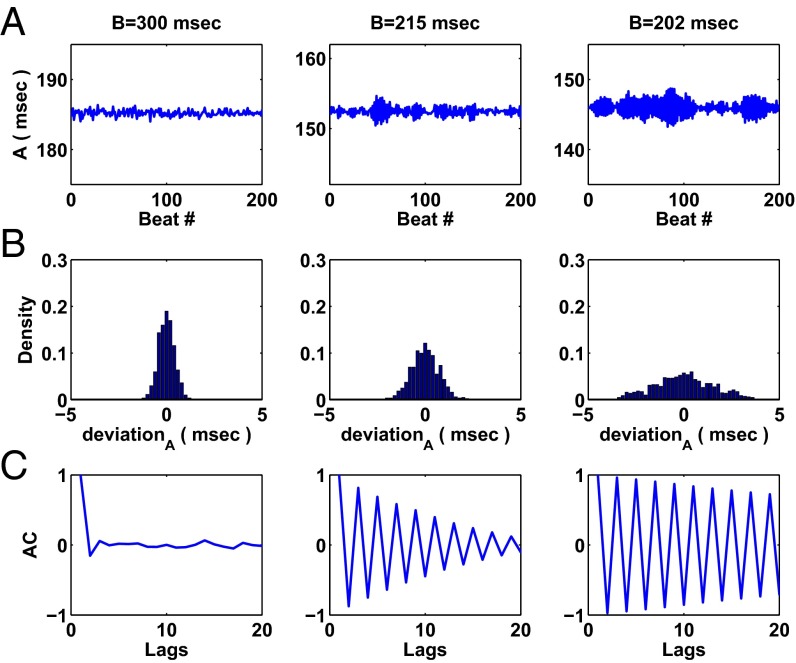
Detection of noise amplification and oscillations in the ACF as a continuously perturbed 2D map simulating action potential duration in response to periodic stimulation approaches a period-doubling bifurcation. (A) Time series of action potential duration—200 values of the variable A from Eq. S1—for three values of stimulus period B: 300 ms (Left), 215 ms (Middle), and 202 ms (Right). The system approaches the period-doubling bifurcation as stimulus period B approaches 200 ms. (B) Histograms of the deviation from the mean computed from 801 values of the action potential duration variable A for three values of stimulus period B. Note that as the system approaches the period-doubling bifurcation, the noise amplifies. (C) ACFs computed from 801 values of the action potential duration variable A computed for the three above values of stimulus period B. Oscillations in the ACF emerge as the system approaches the period-doubling bifurcation. See Fig. S7: Analysis of a Continuously Perturbed 2D Model for a full description of the model and the methods of analysis.
A question remains related to the origin of the noise amplification observed in the experiments. Recent studies examining the onset of beat-to-beat alternations of the action potential duration have implicated the stochastic nature of calcium release from intracellular stores as influencing whole-cell dynamics near a period-doubling bifurcation (43, 44). Furthermore, individual ion channels open and close in a stochastic manner, and channel noise may influence interbeat interval statistics (45). Thus, drug treatment leading to a reduction in the number of functional hERG potassium channels over a long time scale, consistent with what we believe occurs in these experiments, could also account for an amplification in the noise. These represent but two possible mechanisms of noise amplification; understanding the mechanistic properties of this process represents a future research direction.
To date, the study of early warning signals has focused on the nonlinear dynamics near the onset of fold bifurcations. While these bifurcations are relevant in many fields, transitions in dynamical systems can take place through a number of different bifurcations (18). The development and experimental validation of early warning signals for additional bifurcations remains an open research direction.
Materials and Methods
Treatment of Aggregates of Embryonic Chick Cardiac Cells with E4031, a Potassium Channel Blocker.
The experiments with the embryonic chicks were carried out in accordance with the Health and Safety regulations at McGill University. The aggregates were prepared according to the method of DeHaan (35). The ventricles of 7-d-old White Leghorn chicken embryo hearts were dissected and dissociated into single cells by trypsinization. The cells were added to an Erlenmeyer flask containing a culture medium gassed with 5% (vol/vol) CO2, 10% (vol/vol) O2, 85% (vol/vol) N2 (pH 7.4), and placed on a gyratory shaker for 24–48 h at 37 °C. The experiments were conducted 2–6 h after the aggregates were plated. We optically imaged the aggregates’ motion, recording the light-intensity variation of a pixel on the edge of each aggregate. The edge pixel data were then processed through a band-pass filter (cutoff frequencies: 0.1–6.5 Hz). The system used phase-contrast imaging sampled at 40 Hz and a CCD camera (NeuroCD–SM; RedShirtImaging, LLC) at an 80 80 pixel spatial resolution. Recordings were carried out at 35–37 °C.
Detrending the Aggregates’ Interbeat Intervals.
We detrend the interbeat intervals using the detrend function in MATLAB. This function first performs a least-squares linear regression for a sliding window of interbeat intervals. Then the linear regression is subtracted from the raw values of the interbeat intervals, which leaves the deviation from the regression. To compute the histograms of the deviation from the mean in Fig. 2B and the ACFs in Fig. 2C, we use a detrended sliding window composed of 20 beats in all cases. We performed these analyses for larger and smaller window sizes, and the increase in the SD and the oscillations in the ACF were observed robustly.
Numerical Simulations of the Nonlinear 1D Exponential Map.
We simulate Eq. 1 with the following parameter values: 0.804, 1.115, and 2.423. In Fig. 3, we plot the return map, histogram, and ACF for three values of γ: 3.0 (Fig. 3, Left), 1.75 (Fig. 3, Middle), and 1.5 (Fig. 3, Right). For the return maps in Fig. 3, we simulate Eq. 1 starting from a random initial condition for 5,000 values of x, and plot the return map for the last 4,000 x values. We also apply normally distributed system-level noise with an SD 0.01, consistent with the fluctuations associated with the interbeat intervals when the system is far away from the bifurcation. For the histograms, we plot the deviation from the mean x value from the simulations.
Calculation of the Slope Measure and Autocorrelation for the Interbeat Intervals near the Bifurcation.
We first detrend the raw interbeat intervals using the method given above. From the detrended data, we plot return maps based on a sliding window composed of the previous 20 beats. Then we compute a linear regression (least-squares) through each return map, where our slope measure, Fig. 4, represents the slope of the linear regression. We compute the lag-1 autocorrelation coefficient using the autocorr function in MATLAB with a sliding window composed of the previous 20 detrended interbeat intervals.
Calculation of the Slope Measure and Autocorrelation from the Numerical Simulations of a 1D Map Undergoing a Period-Doubling Bifurcation.
We simulate Eq. 1 while linearly decreasing the value of γ such that we simulate the system approaching the period-doubling bifurcation. (We use the same parameter values as given in Materials and Methods describing the numerical simulations.) We apply system-level, normally distributed noise with an SD 0.01, consistent with the fluctuations associated with the interbeat intervals when the system is far away from the bifurcation. We linearly decrease the value of γ along the linear function for the first 300 beats and then the linear function for the remaining 50 beats, where t represents the beat number from the figure. We apply parametric, normally distributed noise with an SD equal to 0.05 to the value of γ, which we calculated by considering a quasi-stationary sequence of the slope measure from the experimental data. We compute the slope measure and the lag-1 autocorrelation coefficient with a sliding window composed of the previous 20 values of x using the same method as given in Materials and Methods.
SI Text
Figs. S1–S3: Treatment of Spontaneously Beating Embryonic Chick Aggregates of Cardiac Cells with the Potassium Channel Blocker E4031.
Fig. S1 displays an image of a representative experiment for which the aggregates are treated with 1.7 μmol E4031. The aggregates are ovoid-shaped and ∼100–300 μm in diameter. One of the main advantages of this experimental approach is that a number of experiments can be performed in parallel. Here, the beat dynamics of 15 aggregates are tracked using the changes in light intensity of a side pixel due to the physical motion of the aggregate. In Fig. S2, we present the raw interbeat interval data for eight aggregates that undergo period-doubling bifurcations. We use these eight aggregates to analyze the slope measure and autocorrelation in Fig. 4. The eight aggregates in Fig. S2 are taken from four different experiments with varying E4031 concentrations (aggregate i: 1 μmol; aggregates ii–v: 2 μmol; aggregate vi: 0.5 μmol; aggregates vii and viii: 1.5 μmol). There are periodic stops in the recording (for ∼2–3 min) for aggregates i–vi in Fig. S2, and data were recorded continuously for aggregates vii and viii. The timing of the onset of the period-doubling bifurcations was between ∼10 min and 55 mins. Of the aggregates we analyzed, 43 out of 104 underwent period-doubling bifurcations. We observed and captured the period-doubling bifurcations for 23 out of 43 cases. In 4 out of 43 aggregates, the system transitioned from a steady, accelerated rhythm through a period-doubling bifurcation. Also, in 16 out of 43 cases, the aggregates underwent period-doubling bifurcations, but, due to stops in the recording, we did not capture the transition according to our definition of the onset of a period-doubling bifurcation. In Fig. S3, we present eight representative examples of beat dynamics from aggregates that, following the treatment of E4031, did not undergo a transition in qualitative dynamics. These eight control aggregates are taken from two experiments (aggregates i–vii: 0.5 μmol; aggregate viii: 2 μmol).
Fig. S4: Analysis of a Continuously Perturbed Linear Map.
To gain mathematical insight into the behavior of the nonlinear 1D map (Eq. 1) in the neighborhood of a period-doubling bifurcation, we analyze a continuously perturbed linear map (Eq. 2) as the slope at the fixed point ( 0) approaches −1. In the paper, we derive analytic expressions for the PDF and the ACF. Here, we show that the analytic expressions for the PDF and the ACF are consistent with numerical simulations. We simulate the linear map for 5,000 values of x applying normally distributed noise with an SD of 0.01 for three values of A, the slope at the fixed point: −0.05 (Fig. S4, Left), −0.65 (Fig. S4, Middle), and −0.95 (Fig. S4, Right). In Fig. S4A, we plot the return maps from the last 4,001 x values, showing that as A approaches −1, the variation of the system increases and successive values of x become increasingly negatively correlated. In Fig. S4B, we plot the histograms of the deviation from the mean for the last 4,000 values of x for the three values of A. We also compute the analytic expression for the PDF (Eq. 3), which is in close agreement with the numerically generated data. Lastly, in Fig. S4C, we show that the numerically generated ACFs—generated using the last 4,000 values of x and the autocorr function in MATLAB—and the analytic expressions for the ACFs (Eq. 4) for the three values of A are consistent.
Fig. S5: Prediction Quality Depends on Early Warning Signal Threshold.
To quantify how the amount of early warning changes as a function of threshold for the 23 aggregates for which we observe and capture period-doubling bifurcations, we perform a survival analysis using Kaplan–Meier plots where we compute estimates of the fraction of aggregates that had not gone through the period-doubling bifurcation as a function of beats before the onset of the transition (Fig. S5). We could only compute estimates of the number of beats before (amount of early warning) due to stops in the recording for 15 of the aggregates included in this analysis. (We added 50 beats to the number of beats before if the slope measure goes through the threshold before a stop in the recording, consistent with the duration of the stop in the recording.) In Fig. S5, we observed that the thresholds −0.75 and −0.6 provide much more early warning than −0.9. For the threshold equal to −0.9, half of the aggregates had gone through the early warning threshold within 11 beats before the transition. However, for thresholds equal to −0.75 and −0.6, half of the aggregates had gone through the early warning threshold within 115 and 195 beats, respectively, before the transition.
Fig. S6: False-Positive Rate Depends on Early Warning Signal Threshold.
We evaluated predictor quality by assessing how the rate of false positives changes as a function of early warning signal threshold from data collected from aggregates for which a transition in dynamics does not take place. Using beat dynamics data from 14 aggregates—totalling ∼17.5 h of control data—we computed the slope measure, and examined how the false positive rate changed as a function of threshold in Fig. S6. Due to the stops in the recording, data from aggregates are divided into a number of individual segments; in particular, each segment is 409.6 s—roughly 7 min—in duration. The data from the 14 aggregates were composed of 155 segments in total. We considered a false positive to have taken place if the slope measure went below the given threshold for five or more consecutive beats at least once in a given segment. For example, if there was exactly one false positive observed in each time segment (out of 155), then the false positive rate would be equal to 1. In Fig. S6, the false positive rate appears to have a sigmoidal shape as a function of threshold. At the threshold value equal to −0.75—given by the red hatched line in Fig. S6—the false positive is 0.02. In particular, for an early warning signal threshold of −0.75, there are three time segments (out of 155) for which a false positive took place.
Fig. S7: Analysis of a Continuously Perturbed 2D Model of Cardiac Alternans.
Recent studies have demonstrated that coupling the action potential duration to a “memory” variable—a variable representing intracellular calcium transients, for example—provides a more accurate representation of period-doubling bifurcations observed in cardiac systems (46). To examine whether noise amplification and oscillations in the ACF emerge in the neighborhood of period-doubling bifurcations in higher-dimensional models, we consider the following continuously perturbed 2D map of the action potential duration in response to periodic stimulation taken from (46, 47):
| [S1] |
| [S2] |
where
| [S3] |
and
| [S4] |
where A is the action potential duration, M is the memory variable, and = 88 ms, E = 122 ms, C = 40 ms, D = 28 ms, =180 ms, and α = 0.2; and are random variables drawn from normal distributions, and σ represents the SD of both random variables, which we set to 0.01 (consistent with the analyses performed on maps throughout the paper). In the deterministic system, the system undergoes a period-doubling bifurcation leading to an alternation in the action potential duration as B goes through ∼200 ms. In Fig. S7, we examine how the system’s noise and autocorrelation change as B approaches the period-doubling bifurcation. In Fig. S7A, we plot A for 200 time steps—these values were taken following 1,200 iterations to account for transients—for three values of B: 300 (Fig. S7A, Left), 215 (Fig. S7A, Middle), and 202 (Fig. S7A, Right). To analyze how the system’s noise changes in the neighborhood of the period-doubling bifurcation, we plotted histograms of the deviation of A values from the mean (n = 801 values of A) from the corresponding simulations for the three values of B (Fig. S7B), showing that, as the system approaches the bifurcation, the noise increases. Lastly, in Fig. S7C, we plot the ACF, generated numerically using the last 801 values of A using the autocorr function in MATLAB, and show that oscillations emerge in the ACF of the system as the bifurcation is approached. Thus, because the dynamics of the 2D map become enslaved to the eigenvalue that is approaching −1 near the period-doubling bifurcation (the slow mode), noise amplification and oscillations in the ACF represent early warning signals for period-doubling bifurcations in higher-dimensional maps as well as 1D maps (as demonstrated in the theoretical analysis given in the paper).
Acknowledgments
We thank Min-Young Kim and Alex Hodge for carrying out the experiments. We would also like to thank Matthew Leavitt and Lennart Hilbert for helpful discussions. This work was supported by the Heart and Stroke Foundation of Canada, Canadian Institutes of Health Research, and Natural Sciences and Engineering Research Council of Canada.
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1424320112/-/DCSupplemental.
References
- 1.Scheffer M, et al. Early-warning signals for critical transitions. Nature. 2009;461(7260):53–59. doi: 10.1038/nature08227. [DOI] [PubMed] [Google Scholar]
- 2.Dakos V, et al. Slowing down as an early warning signal for abrupt climate change. Proc Natl Acad Sci USA. 2008;105(38):14308–14312. doi: 10.1073/pnas.0802430105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Lenton TM. Early warning of climate tipping points. Nat Clim Chang. 2011;1(4):201–209. [Google Scholar]
- 4.May RM. Thresholds and breakpoints in ecosystems with a multiplicity of stable states. Nature. 1977;269(5628):471–477. [Google Scholar]
- 5.Carpenter SR, Brock WA. Rising variance: A leading indicator of ecological transition. Ecol Lett. 2006;9(3):311–318. doi: 10.1111/j.1461-0248.2005.00877.x. [DOI] [PubMed] [Google Scholar]
- 6.Dai L, Vorselen D, Korolev KS, Gore J. Generic indicators for loss of resilience before a tipping point leading to population collapse. Science. 2012;336(6085):1175–1177. doi: 10.1126/science.1219805. [DOI] [PubMed] [Google Scholar]
- 7.Dai L, Korolev KS, Gore J. Slower recovery in space before collapse of connected populations. Nature. 2013;496(7445):355–358. doi: 10.1038/nature12071. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Dakos V, Bascompte J. Critical slowing down as early warning for the onset of collapse in mutualistic communities. Proc Natl Acad Sci USA. 2014;111(49):17546–17551. doi: 10.1073/pnas.1406326111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.McSharry PE, Smith LA, Tarassenko L. Prediction of epileptic seizures: Are nonlinear methods relevant? Nat Med. 2003;9(3):241–242, author reply 242. doi: 10.1038/nm0303-241. [DOI] [PubMed] [Google Scholar]
- 10.Kramer MA, et al. Human seizures self-terminate across spatial scales via a critical transition. Proc Natl Acad Sci USA. 2012;109(51):21116–21121. doi: 10.1073/pnas.1210047110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.May RM, Levin SA, Sugihara G. Complex systems: Ecology for bankers. Nature. 2008;451(7181):893–895. doi: 10.1038/451893a. [DOI] [PubMed] [Google Scholar]
- 12.Kuehn C. A mathematical framework for critical transitions: Bifurcations, fast–slow systems and stochastic dynamics. Phys D. 2011;240(12):1020–1035. [Google Scholar]
- 13.Ditlevsen PD, Johnsen SJ. Tipping points: Early warning and wishful thinking. Geophys Res Lett. 2010;37(19):L19703. [Google Scholar]
- 14.Wieczorek S, Ashwin P, Luke CM, Cox PM. Excitability in ramped systems: The compost-bomb instability. Proc R Soc A. 2011;467(2129):1243–1269. [Google Scholar]
- 15.Ashwin P, Wieczorek S, Vitolo R, Cox P. Tipping points in open systems: Bifurcation, noise-induced and rate-dependent examples in the climate system. Philos Trans R Soc A. 2012;370(1962):1166–1184. doi: 10.1098/rsta.2011.0306. [DOI] [PubMed] [Google Scholar]
- 16.Hastings A, Wysham DB. Regime shifts in ecological systems can occur with no warning. Ecol Lett. 2010;13(4):464–472. doi: 10.1111/j.1461-0248.2010.01439.x. [DOI] [PubMed] [Google Scholar]
- 17.Wang R, et al. Flickering gives early warning signals of a critical transition to a eutrophic lake state. Nature. 2012;492(7429):419–422. doi: 10.1038/nature11655. [DOI] [PubMed] [Google Scholar]
- 18.Chen A, Sanchez A, Dai L, Gore J. Dynamics of a producer-freeloader ecosystem on the brink of collapse. Nat Commun. 2014;5:3713. doi: 10.1038/ncomms4713. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Pastore JM, Girouard SD, Laurita KR, Akar FG, Rosenbaum DS. Mechanism linking T-wave alternans to the genesis of cardiac fibrillation. Circulation. 1999;99(10):1385–1394. doi: 10.1161/01.cir.99.10.1385. [DOI] [PubMed] [Google Scholar]
- 20.Gizzi A, et al. Effects of pacing site and stimulation history on alternans dynamics and the development of complex spatiotemporal patterns in cardiac tissue. Front Physiol. 2013;4:71. doi: 10.3389/fphys.2013.00071. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Watanabe MA, Fenton FH, Evans SJ, Hastings HM, Karma A. Mechanisms for discordant alternans. J Cardiovasc Electrophysiol. 2001;12(2):196–206. doi: 10.1046/j.1540-8167.2001.00196.x. [DOI] [PubMed] [Google Scholar]
- 22.Sato D, Bers DM, Shiferaw Y. Formation of spatially discordant alternans due to fluctuations and diffusion of calcium. PLoS One. 2013;8(12):e85365. doi: 10.1371/journal.pone.0085365. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Rosenbaum DS, et al. Electrical alternans and vulnerability to ventricular arrhythmias. N Engl J Med. 1994;330(4):235–241. doi: 10.1056/NEJM199401273300402. [DOI] [PubMed] [Google Scholar]
- 24.Verrier RL, et al. Microvolt T-wave alternans physiological basis, methods of measurement, and clinical utility–Consensus guideline by International Society for Holter and Noninvasive Electrocardiology. J Am Coll Cardiol. 2011;58(13):1309–1324. doi: 10.1016/j.jacc.2011.06.029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Guevara M, Ward G, Shrier A, Glass L. Electrical alternans and period doubling bifurcations. IEEE Comp Cardiol. 1984;562:167–170. [Google Scholar]
- 26.Echebarria B, Karma A. Instability and spatiotemporal dynamics of alternans in paced cardiac tissue. Phys Rev Lett. 2002;88(20):208101. doi: 10.1103/PhysRevLett.88.208101. [DOI] [PubMed] [Google Scholar]
- 27.Echebarria B, Karma A. Amplitude equation approach to spatiotemporal dynamics of cardiac alternans. Phys Rev E Stat Nonlin Soft Matter Phys. 2007;76(5 Pt 1):051911. doi: 10.1103/PhysRevE.76.051911. [DOI] [PubMed] [Google Scholar]
- 28.Guevara MR, Glass L, Shrier A. Phase locking, period-doubling bifurcations, and irregular dynamics in periodically stimulated cardiac cells. Science. 1981;214(4527):1350–1353. doi: 10.1126/science.7313693. [DOI] [PubMed] [Google Scholar]
- 29.Fenton FH, Gizzi A, Cherubini C, Pomella N, Filippi S. Role of temperature on nonlinear cardiac dynamics. Phys Rev E Stat Nonlin Soft Matter Phys. 2013;87(4):042717. doi: 10.1103/PhysRevE.87.042717. [DOI] [PubMed] [Google Scholar]
- 30.Karagueuzian HS, et al. Action potential alternans and irregular dynamics in quinidine-intoxicated ventricular muscle cells. Implications for ventricular proarrhythmia. Circulation. 1993;87(5):1661–1672. doi: 10.1161/01.cir.87.5.1661. [DOI] [PubMed] [Google Scholar]
- 31.Quail T, et al. Chaotic dynamics in cardiac aggregates induced by potassium channel block. Chaos. 2012;22(3):033140. doi: 10.1063/1.4748854. [DOI] [PubMed] [Google Scholar]
- 32.Hao Bl. Universal slowing-down exponent near period-doubling bifurcation points. Phys Lett A. 1981;86(5):267–268. [Google Scholar]
- 33.Wiesenfeld K. Noisy precursors of nonlinear instabilities. J Stat Phys. 1985;38(5-6):1071–1097. [Google Scholar]
- 34.Kim MY, et al. Stochastic and spatial influences on drug-induced bifurcations in cardiac tissue culture. Phys Rev Lett. 2009;103(5):058101. doi: 10.1103/PhysRevLett.103.058101. [DOI] [PubMed] [Google Scholar]
- 35.DeHann RL. Regulation of spontaneous activity and growth of embryonic chick heart cells in tissue culture. Dev Biol. 1967;16(3):216–249. doi: 10.1016/0012-1606(67)90025-5. [DOI] [PubMed] [Google Scholar]
- 36.Clay JR, Kristof AS, Shenasa J, Brochu RM, Shrier A. A review of the effects of three cardioactive agents on the electrical activity from embryonic chick heart cell aggregates: TTX, ACh, and E-4031. Prog Biophys Mol Biol. 1994;62(3):185–202. doi: 10.1016/0079-6107(94)90011-6. [DOI] [PubMed] [Google Scholar]
- 37.Clusin WT, Hamilton WE, Nelson DV. The mechanical activity of chick embryonic myocardial cell aggregates. J Physiol. 1981;320(1):149–174. doi: 10.1113/jphysiol.1981.sp013941. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Talkner P, Hänggi P. In: Noise in Nonlinear Dynamical Systems. Moss F, McClintock P, editors. Vol 2. Cambridge Univ Press; New York: 1989. pp. 87–99. [Google Scholar]
- 39.Surovyatkina E. Rise and saturation of the correlation time near bifurcation threshold. Phys Lett A. 2004;329(3):169–172. [Google Scholar]
- 40.Boettiger C, Hastings A. Quantifying limits to detection of early warning for critical transitions. J R Soc Interface. 2012;9(75):2527–2539. doi: 10.1098/rsif.2012.0125. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Dakos V, Carpenter SR, van Nes EH, Scheffer M. Resilience indicators: Prospects and limitations for early warnings of regime shifts. Philos Trans R Soc B. 2015;370(1659):20130263. [Google Scholar]
- 42.Zhao X, Schaeffer DG, Berger CM, Gauthier DJ. Small-signal amplification of period-doubling bifurcations in smooth iterated maps. Nonlinear Dyn. 2007;48(4):381–389. doi: 10.1007/s11071-006-9092-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Restrepo JG, Karma A. Spatiotemporal intracellular calcium dynamics during cardiac alternans. Chaos. 2009;19(3):037115. doi: 10.1063/1.3207835. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Alvarez-Lacalle E, Echebarria B, Spalding J, Shiferaw Y. Calcium alternans is due to an order-disorder phase transition in cardiac cells. Phys Rev Lett. 2015;114(10):108101. doi: 10.1103/PhysRevLett.114.108101. [DOI] [PubMed] [Google Scholar]
- 45.White JA, Klink R, Alonso A, Kay AR. Noise from voltage-gated ion channels may influence neuronal dynamics in the entorhinal cortex. J Neurophysiol. 1998;80(1):262–269. doi: 10.1152/jn.1998.80.1.262. [DOI] [PubMed] [Google Scholar]
- 46.Tolkacheva EG, Romeo MM, Guerraty M, Gauthier DJ. Condition for alternans and its control in a two-dimensional mapping model of paced cardiac dynamics. Phys Rev E Stat Nonlin Soft Matter Phys. 2004;69(3 Pt 1):031904. doi: 10.1103/PhysRevE.69.031904. [DOI] [PubMed] [Google Scholar]
- 47.Fox JJ, Bodenschatz E, Gilmour RF., Jr Period-doubling instability and memory in cardiac tissue. Phys Rev Lett. 2002;89(13):138101. doi: 10.1103/PhysRevLett.89.138101. [DOI] [PubMed] [Google Scholar]