Modified SuperCurve Method for Analysis of Reverse-Phase Protein Array Data

Abstract

Reverse-phase protein arrays (RPPAs) are widely used in biological and biomedical fields of study. One of the most popular analytic methods in RPPA data analysis is the SuperCurve method, which requires estimation of the background fluorescence level. This estimation is usually not accurate and has sample bias and spatial bias. Here, we propose a taking-the-difference method to overcome this problem. Briefly, for each two consecutive RPPA cycles, we subtract the later cycle from the earlier cycle, transforming the m-cycle data into m−1 cycle of data. This removes most of the background fluorescence noise. We then use the m−1 cycle of data to fit a new model accordingly derived from the SuperCurve model. To evaluate our proposed method, we compare the accuracy and precision between our proposed model and the original SuperCurve model by testing them on both real and simulated datasets. For both situations, our modified model shows improved results. The modified SuperCurve method is easy to perform and the taking-the-difference idea is recommended for application to all current methods of RPPA data analysis.

1. Introduction

The reverse-phase protein array (RPPA) is commonly used as an analytical method in proteomics and has been successfully applied in capturing disease progression (Paweletz et al., 2001), signal pathway detection (Charboneau et al., 2002), analysis of proteomic profiling (Nishizuka et al., 2003), biomarker discovery in drug development (Wilson and Nock, 2003), and in other types of studies. RPPA provides several advantages. First, it does not require direct labeling on the sample or two-site antibody. Therefore, there will be no experimental variability due to labeling yield (Liotta et al., 2003). Second, with RPPA, all samples are spotted at the same time, which enables this method to represent the underlying disease signal transactions for the whole cell (Tabus et al., 2006). Third, as each sample is exposed to the same concentrations of primary and secondary antibodies for the same period of time, subtle differences in analytes can be captured (Liotta et al., 2003). In addition, each protein sample in the reverse-phase array has a calibration curve. This provides a better means for matching the antibody concentration and the analyte concentration (Sheehan et al., 2005).

Multiple methods have been applied for the analysis of RPPA data. The sigmoidal shape has been chosen as it is consistent with the expected relationship of observed signal and true protein concentration (Tabus et al., 2006). This method has been developed as the “SuperCurve” method and is publicly available online through the Department of Bioinformatics and Computational Biology at the University of Texas MD Anderson Cancer Center. Hu et al. (2007) proposed a more flexible nonparametric joint sample model for RPPA analysis. Troncale et al. (2012) proposed a new method, called NormaCurve, which allows for the normalization of RPPA data. All the above analytical methods require the step of background correction. However, there are problems caused by background corrections (Rao et al., 2013). First, incorrect background subtraction leads to miscalculation of protein efficiency (Shain and Clemens, 2008). Second, background noise varies when different models are applied (Guescini et al., 2008). Third, all the methods assume a constant background for all samples within one RPPA experiment; however, this assumption usually does not hold in reality. Different areas of an RPPA array may have different background fluorescence levels.

In this study, we modify the SuperCurve method to minimize the influence introduced by background noise. The idea is that the data are in a time series structure, and differentiating among the data is an approach that is commonly used for this kind of data (Diggle, 1990). For each sample, we subtract each later dilution cycle from its previous dilution cycle, transforming the m-cycle data into m−1 cycles. By subtracting, most of the background noise is removed. The SuperCurve model for m-cycle data implies a model for the m−1 cycle of data. We simplify the model by using Taylor's expansion so that linear regression techniques can be applied to fit the model. We demonstrate through real and simulated datasets that the proposed method improves data analysis results.

2. Methods

SuperCurve is a logistic model with three global parameters (Hu et al., 2007).

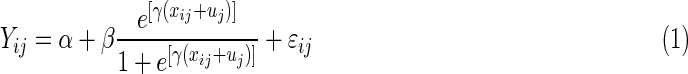For notation, Y_ij is the observed signal intensity for dilution i of sample j, where 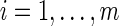and 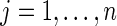. Typically, x_ij= (1+m)/2 −i for all j. The median effective protein concentration is u_j, which is the 50th percentile of the series protein dataset. It is the parameter of interest. The known dilution offset step is x_ij. The global parameters for the curve are α, β, and γ, where α represents the background fluorescence in the model, and the error term is ɛ_ij ∼ N(0, σ²).

Based on our idea, we build an m−1 cycle of data Z_ij from Y_ij so that we can remove α.

RPPA data are serial diluted. The data in the later step should be theoretically smaller than the data in the previous step. Thus, the Z's should always be nonnegative. Negative Z's are not used in the data analysis below.

We then use the new m−1 cycle of data to fit the SuperCurve model. Denoting x_ij+u_j=t, we obtain the log form of Z_ij as

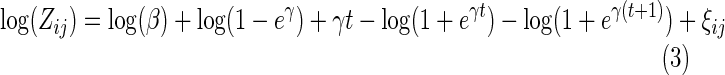By Taylor's series, we obtain . Then, Equation (3) becomes

It is a linear regression function of log(Z_ij) on , , , 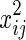and x_ij. We assume that θ₁ is the coefficient for 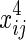and θ₂ is the coefficient for 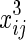. Then, after calculations, we obtain u_j, as shown below:

We may conduct a separate linear regression for each sample. However, to borrow strength between samples, we use a linear mixed model (Stroup et al., 2012) to estimate the above parameters. By implementing the mixed model, we obtain the median protein effect concentration for each sample. Also, we assume that there is a constant noise level on a Z scale. Then, by the delta method, the variance of the noise level at the log(Z) level is proportional to the inverse of Z². To further improve our method, we incorporate a weight with 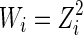into the mixed model. Then, we can obtain u_j for each sample, which is the median effective concentration.

We apply the above modified SuperCurve method and the original SuperCurve method to simulated and real data sets. We used three criteria to compare them: relative error (RE), mean squared error (MSE), and coefficient of variation (CV), as defined below.

where 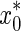is the estimated protein concentration effect and x₀ is the true protein concentration effect of each of the n samples. A model with smaller RE and MSE is more accurate. We also used the CV to test the precision of the methods, as shown below.

In Equation (8), s and 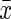are the respective standard deviation and the mean of the protein concentrations. A smaller CV represents a more precise method. We used the CV to compare the precision of the models in the practical dataset and used RE, CV, and MSE to compare both precision and accuracy in the simulated datasets.

3. Results

The simulated dataset we used was developed by Hu et al. (2007). The signals were generated based on the SuperCurve model in Equation (1) with β=10,000 and γ=3. A common set of true u_j was selected from a normal distribution, with mean 1.0 and standard deviation 1.5. There were 1000 samples and 5 dilution cycles for each sample. The background level α was generated from a normal distribution, with mean 4000 and standard deviation 1000. We compared the value of the RE, CV, and MSE between the result obtained from the SuperCurve model and that from the modified SuperCurve model as described in the Methods section.

Table 1 shows the comparison of the mean values over the 1000 samples of RE, CV, and MSE for the SuperCurve method and the modified SuperCurve model as applied to the simulated dataset. The RE obtained by the modified SuperCurve method was 1.16, which was smaller than that obtained by the SuperCurve method (6.33). The MSE obtained by our modified model was 4.07, which was smaller than the corresponding value obtained by the SuperCurve model (7.63). The absolute value of CV for our modified method was 0.56, which was much smaller than that obtained in the original SuperCurve model (12.55). The original SuperCurve method yielded 14 outlier results (estimated μ_j >50) when analyzing the simulated dataset. These outliers were not included in the calculation of the above RE, MSE, and CV. Our proposed method did not give any such outliers.

Table 1.

Comparison of Relative Error, Coefficient of Variation, and Mean Squared Error Between the SuperCurve Method and the Modified SuperCurve Method when Applied to the Simulated Dataset

Criteria	SuperCurve	Modified SuperCurve
Relative error	6.33	1.16
Mean squared error	7.63	4.07
Coefficient of variation	12.55	−0.56

We used a real experimental dataset provided by Troncale et al. (2012). We selected 390 samples from the dataset, all of which have the same initial protein inputs (1 mg/ml) and fifteen 2-fold serial dilutions (1, ½, ¼, 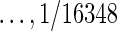). For convenience, we used only the first five data dilution cycles in our data analysis. Most RPPA experiments use only five dilutions.

The samples in this dataset had the same initial protein inputs and dilution steps, and so it was convenient for us to compare the CVs using different algorithms. The absolute value of CV for the SuperCurve model was 17.47, which was much larger than that in our modified model (8.18), indicating that our modified model can improve precision compared to the original model.

4. Discussion

This study describes the incorporation of the taking-the-difference strategy in the SuperCurve method for RPPA data analysis. The modified method is theoretically more advantageous as it does not require the step of background correction. We compared our modified method with the original method in terms of accuracy and precision. Applied to the real dataset, our modified method showed more precision than the original method. Applied to the simulated dataset, our modified method showed better results in terms of accuracy and precision, even after removing the outliers generated by the SuperCurve model.

The advantages of our model are the ability to avoid the background noise effect and to generate results with less variance after fitting the mixed model. This advantage is particularly important when analyzing datasets with relatively large variance and background noise levels.

The original SuperCurve method includes a process of removing outliers, whereas our modified method does not. The NormaCurve method introduced a helpful normalization process (Troncale et al., 2012). Further work may incorporate a process of diagnostics and data normalization in our modified method to further improve its accuracy and precision.

Overall, our modified SuperCurve method is valuable for RPPA data analysis. It is easy to perform and can avoid errors introduced by background subtraction. We recommend the application of this taking-the-difference approach in all current methods for RPPA data analysis.

Acknowledgments

This research was supported by the U.S. National Institutes of Health Grants U54 CA096300, U01 CA152958, and 5P50 CA100632.

Author Disclosure Statement

No competing financial interests exist.