Penalized Q-Learning for Dynamic Treatment Regimens

Abstract

A dynamic treatment regimen incorporates both accrued information and long-term effects of treatment from specially designed clinical trials. As these trials become more and more popular in conjunction with longitudinal data from clinical studies, the development of statistical inference for optimal dynamic treatment regimens is a high priority. In this paper, we propose a new machine learning framework called penalized Q-learning, under which valid statistical inference is established. We also propose a new statistical procedure: individual selection and corresponding methods for incorporating individual selection within penalized Q-learning. Extensive numerical studies are presented which compare the proposed methods with existing methods, under a variety of scenarios, and demonstrate that the proposed approach is both inferentially and computationally superior. It is illustrated with a depression clinical trial study.

1. Introduction

Developing effective therapeutic regimens for diseases is one of the essential goals of medical research. Two major design and analysis challenges in this effort are taking accrued information into account in clinical trial designs and effectively incorporating long-term benefits and risks of treatment due to delayed effects. One of the most promising approaches to deal with these two challenges has been recently referred to as dynamic treatment regimens or adaptive treatment strategies (Murphy, 2003), and has been used in a number of settings, such as drug and alcohol dependency studies.

Reinforcement learning, one of the primary tools used in developing dynamic treatment regimens, is a sub-area of machine learning, where the learning behavior is through trial-and-error interactions with a dynamic environment (Kaelbling et al., 1996). Because reinforcement learning techniques have been shown to be effective in developing optimal dynamic treatment regimens, the area is attracting increased attention among statistical researchers. As a recent example, a new approach to cancer clinical trials based on the specific area of reinforcement learning called Q-learning, has been proposed by Zhao et al. (2009) and Zhao et al. (2011). Extensive statistical estimating methods have also been proposed for optimal dynamic treatment regimens, including, for example, Chakraborty et al. (2010), who developed a Q-learning framework based on linear models. Other related literature includes likelihood-based methods (Thall et al., 2000, 2002, 2007) and semiparametric methods (Murphy, 2003; Robins, 2004; Lunceford et al., 2002; Wahed and Tsiatis, 2004, 2006; Moodie et al., 2009).

In contrast to the substantial body of estimating methods, the development of statistical inference for optimal dynamic treatment regimens is very limited. This sequential, multi-stage decision making problem is at the intersection of machine learning, optimization and statistical inference and is thus quite challenging. As discussed in Robins (2004), and recognized by many other researchers, the challenge arises when the optimal last stage treatment is non-unique for at least some subjects in the population, causing estimation bias and failure of traditional inferential approaches. There have been a number of proposals to correct this. For example, Moodie and Richardson (2010) proposed a method called Zeroing Instead of Plugging In. This is referred to as the hard-threshold estimator by Chakraborty et al. (2010), who also proposed a soft-threshold estimator and implemented several bootstrap methods. There is, however, a lack of theoretical support for these methods. Moreover, simulations indicate that neither hard-thresholding nor soft-thresholding, in conjunction with their bootstrap implementation, works uniformly well. We are therefore motivated to develop improved, asymptotically valid inference for optimal dynamic treatment regimens.

In this paper, we develop a new reinforcement learning framework for discovering optimal dynamic treatment regimens: penalized Q-learning. The major distinction of penalized Q-learning from traditional Q-learning is in the form of the objective Q-function at each stage. While the new method shares many of the properties of traditional Q-learning, it has some significant advantages. Based on penalized Q-learning, we propose effective inferential procedures for optimal dynamic treatment regimens. In contrast to existing bootstrap approaches, our variance calculations are based on explicit formulae and hence are much less time-consuming. Theoretical studies and extensive empirical evidence support the validity of the proposed methods. Since penalized Q-learning puts a penalty on each individual, it automatically initiates another procedure, individual selection, which selects those individuals without treatment effects from the population. Successful individual selection, i.e., correctly identifying individuals without treatment effects, is the key to improved statistical inference.

While the proposed individual selection procedure shares some similarities with certain commonly used variable selection methods, the approaches differ fundamentally in other ways. These issues will be addressed in greater detail below.

2. Statistical Inference with Q-learning

2.1. Personalized Dynamic Treatment Regimens

We now introduce the multi-stage decision problem, since we illustrate with two-stage clinical trial data. Consider data from a sequential multiple assignment randomized trial (SMART), where treatments are randomized at multiple stages (Lavori and Dawson, 2000; Murphy, 2005). The longitudinal data on each patient take the form $H={(H_1^T,H_2^T)}^T$ Where $H_1={(O_1^T,A_1,R_1)}^T,H_2={(O_2^T,A_2,R_2)}^T$ are sequences of random variables collected at two stages, t = 1, 2. As components of H _t, A_t is the randomly assigned treatment to patients, O_t is the observed patient covariates prior to the treatment assignment and R_t is the clinical outcome, each at stage t. The observed data consist of n independent and identically distributed copies of H. Our goal is to estimate the best treatment decision for different patients using the observed data at each stage. This is equivalent to identifying a sequence of ordered rules, which we call a personalized dynamic treatment regimen, d = (d₁, d₂)^T , one rule for each stage, mapping from the domain of the patient history S _t, 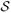_t, to the domain of treatment A_t, 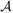_t, where S₁ = O₁ and $S_2={(O_1^T,A_1,R_1,O_2^T)}^T$.

Denote the distribution of H by P and the expectations with respect to this distribution by E. Let P^d denote the distribution of H and the expectations with respect to this distribution by E^d where the dynamic treatment regimen d(·) is used to assign treatments. Define the value function to be V(d) = E^d(R₁ + R₂). Thus, an optimal dynamic treatment regimen, d₀, is a rule that has the maximal value, i.e., d₀ ∈ arg max_dV (d). We use upper case letters to denote random variables and lower case letters to denote values of the random variables. In this two-stage setting, if we define Q₂(s₂, a₂) = E(R₂|S₂ = s₂, A₂ = a₂) and Q₁(s₁, a₁) = E(R₁ + max_{a2∈ 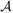2} Q₂(S₂, a₂)|S₁ = s₁, A₁ = a₁), then the optimal decision rule at time t is d_t(s_t) = argmax_{at∈ 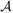t} Q_t(s_t, a_t), where Q_t are the Q-functions at time t.

2.2. Q-learning for personalized dynamic treatment regimens

Q-learning is a backward recursive approach commonly used for estimating the optimal personalized dynamic treatment regimens. Following Chakraborty et al. (2010), let the Q-function for time t = 1, 2 be modeled as

$$Q_t(S_t,A_t;{\beta }_t,{\psi }_t)={\beta }_t^T{S}_{t(1)}+({\psi }_t^T{S}_{t(2)})A_t,$$ (2.1)

where S_t is the full state information at time t introduced in the previous section and S_t(1) and S_t(2) are given features as functions of S_t. For example, they can be subsets of S_t selected for the model. They can be identical or different. Moreover, the constant 1 is included in S_t(1) and S_t(2). The action A_t takes value 1 or −1. The parameters of the Q-function are ${\theta }_t={({\beta }_t^T,{\psi }_t^T)}^T,$ where β_t reflects the main effect of current state on outcome, while ψ_t reflects the interaction effect between current state and treatment choice. The true values of these parameters are denoted θ_t0, β_t0, and ψ_t0 respectively. We note that the additive formulation of rewards is not restrictive. In fact, we can always define the intermediate rewards to be zeros while the final stage reward to be the final outcome we are interested in. This won't change the value function we aim to maximize. The linear models studied here are also general if we let state variables in the regression be some basis functions of historical variables (for instance, using kernel machine). Furthermore, one can always perform model diagnostics to check linearity assumption.

Suppose that the observed data consist of (S_ti, A_ti, R_ti) for patients i = 1,…, n and t = 1, 2, from a sample of n independent patients. The two-stage empirical version of the Q-learning procedure can be summarized as follows:

• Step 1. Start with a regular and non-shrinkage estimator, based on least squares, for the second stage:

  $$\stackrel{\sim }{{\theta }_2}={({\stackrel{\sim }{\beta }}_2^T,{\stackrel{\sim }{\psi }}_2^T)}^T={argmin}_{{\beta }_2,{\psi }_2}\sum _{i=1}^n{\{R_{2i}-Q_2(S_{2i},A_{2i};{\beta }_2,{\psi }_2)\}}^2={\left(Z_2^T{Z}_2\right)}^{-1}{Z}_2^T{R}_2,$$

  Where θ̃₂ is the least squares estimator, Z₂ is the stage-2 design matrix with each row of $(S_{2i(1)}^T,A_{2i}{S}_{2i(2)}^T)$ and R₂ = (R₂₁,…, R_2n)^T. Here and in the sequel, S_ti(k) denotes the kth component of S_t for subject i, where k = 1, 2, t = 1, 2 and i = 1,…, n.

• Step 2. Estimate the first-stage individual pseudo-outcome by ${\widehat{Y}}_1^{\text{HM}}={({\widehat{Y}}_{11}^{\text{HM}},\dots ,{\widehat{Y}}_{1n}^{\text{HM}})}^T$, Where

  $${\widehat{Y}}_{1i}^{\text{HM}}=R_{1i}+{max}_{a\in \{-1,1\}}{Q}_2(S_{2i},a;{\stackrel{\sim }{\theta }}_2)=R_{1i}+{\stackrel{\sim }{\beta }}_2^T{S}_{2i(1)}+|{\stackrel{\sim }{\psi }}_2^T{S}_{2i(2)}|$$ (2.2)

  where ^HM is the index for the hard-max estimator.

• Step 3. Estimate the first-stage parameters by least squares estimation:

  $${\stackrel{\sim }{\theta }}_1^{\text{HM}}={argmin}_{{\beta }_1,{\psi }_1}\sum _{i=1}^n{\{{\widehat{Y}}_{1i}^{\text{HM}}-Q_1(S_{1i},A_{1i};{\beta }_1,{\psi }_1)\}}^2={\left(Z_1^T{Z}_1\right)}^{-1}{Z}_1^T{\widehat{Y}}_1^{\text{HM}},$$

  where Z₁ is the stage-1 design matrix whose ith row is $(S_{1i(1)}^T,A_{1i}{S}_{1i\left(2\right)}^T)$. The corresponding estimator of ψ₁, denoted by ${\widehat{\psi }}_1^{\text{HM}}$, is referred to as the hard max estimator in Chakraborty et al. (2010), because of the maximizing operation used in the definition.

2.3. Challenges in Statistical Inference

When the Q-function takes the linear model form (2.1), the optimal dynamic treatment regimen for patient i is

$$d_i(s_{ti})={argmax}_{a_i\in \{-1,1\}}({\psi }_t^T{s}_{ti(2)})a_i=\text{sgn}({\psi }_t^T{s}_{ti(2)}),t=1,2,i=1,\dots ,n.$$

where sgn(x) = 1 if x > 0 and −1 otherwise. We use s_ti to denote the observed value of S_t for patient i and s_ti(k) denotes the observed value of S_t(k) for stage t = 1, 2, component k = 1, 2 and patient i. The parameters ψ₂ are of particular interest for inference on the optimal dynamic treatment regimen, as ψ₂ represents the interaction effect of the treatment and covariates.

During the Q-learning procedure, when there is a positive probability that ${\psi }_{20}^T{S}_{2(2)}=0$, the first-stage hard max pseudo-outcome ${\widehat{Y}}_1^{\text{HM}}$ is a non-smooth function of ψ~₂ As a linear function of ${\widehat{Y}}_1^{\text{HM}}$, the hard max estimator ${\widehat{\psi }}_1^{\text{HM}},$ is also a non-smooth function of ψ~₂ Consequently, the asymptotic distribution of $n^{1/2}({\widehat{\psi }}_1^{\text{HM}}-{\psi }_{10})$ is neither normal nor any well-tabulated distributions if $\text{Pr}({\psi }_{20}^T{S}_{2(2)}=0)>0$. In this non-standard case, standard inference methods such as Wald-type confidence intervals are no longer valid.

2.4. Review of Existing Approaches

To overcome the difficulty of inference for ψ₁ in Q-learning, several methods have been proposed, which we briefly review in the two-stage set-up. Since all the methods are also nested in the Q-learning procedure, we update the two-stage version of Q-learning as follows.

• Step 2. Estimate the first-stage individual pseudo-outcome by shrinking the second-stage regular estimators via hard-thresholding or soft-thresholding. Specifically, the hard-threshold pseudo-outcome is denoted ${\widehat{Y}}_1^{\text{HT}}={({\widehat{Y}}_{11}^{\text{HT}},\dots ,{\widehat{Y}}_{1n}^{\text{HT}})}^T,$ with

  $${\widehat{Y}}_{1i}^{\text{HT}}=R_{1i}+{\stackrel{\sim }{\beta }}_2^T{S}_{2i(1)}+|{\stackrel{\sim }{\psi }}_2^T{S}_{2i(2)}|1\{\frac{n^{1/2}|{\stackrel{\sim }{\psi }}_2^T{S}_{2i(2)}|}{{(S_{2i(2)}^T{\widehat{\sum }}_2{S}_{2i(2)})}^{1/2}}>z_{\alpha /2}\},$$ (2.3)
  Where Σ̂₂/n is the estimated covariance matrix of ψ~₂, α is a pre-specified significance level and z_α/2 is the (1 − α/2)-quantile of the standard normal distribution. The soft-threshold pseudo-outcome is denoted ${\widehat{Y}}_1^{\text{ST}}={({\widehat{Y}}_{11}^{\text{ST}},\dots ,{\widehat{Y}}_{1n}^{\text{ST}})}^T$, with

  $${\widehat{Y}}_{1i}^{\text{ST}}=R_{1i}+{\stackrel{\sim }{\beta }}_2^T{S}_{2i(1)}+|{\stackrel{\sim }{\psi }}_2^T{S}_{2i(2)}|{(1-\frac{{\lambda }_i}{|{\stackrel{\sim }{\psi }}_2^T{S}_{2i(2)}|})}_{+},i=1,\dots ,n,$$ (2.4)

  where x₊ = xI{x > 0} and λ_i is a tuning parameter.

• Step 3. Estimate the first-stage parameters by least squares estimation:

  $${\widehat{\theta }}_1^{º}={({\widehat{\beta }}_1^{ºT},{\widehat{\psi }}_1^{ºT})}^T={argmin}_{{\beta }_1,{\psi }_1}\sum _{i=1}^n{\{{\widehat{Y}}_{1i}^{º}-Q_1(S_{1i},A_{1i};{\beta }_1,{\psi }_1)\}}^2={\left(Z_1^T{Z}_1\right)}^{-1}{Z}_1^T{\widehat{Y}}_1^{º},$$

  Where Ŷ₁^º is either a hard-threshold or soft-threshold pseudo-outcome, as defined in either (2.3) or (2.4), respectively. The corresponding estimator of ψ₁, denoted ${\widehat{\psi }}_1^{º}$, can be the hard-threshold estimator ${\widehat{\psi }}_1^{\text{HT}}$ or the soft-threshold estimator ${\widehat{\psi }}_1^{\text{ST}}$.

The hard-thresholding and soft-thresholding methods can be viewed as upgraded versions of the hard max methods in terms of reducing the degree of non-differentiability of the absolute value function at zero. The first-stage pseudo-outcome for these three existing methods can be viewed as shrinkage functionals of certain standard estimators. Even if these estimators form shrinkage estimators under certain conditions, they are not optimizers of reasonable objective functions in general. Consequently, even if these estimators can successfully achieve shrinkage, two drawbacks remain that negate their ability to be used for statistical inference for optimal dynamic treatment regimens. First, the bias of these first-stage pseudo-outcomes can be large in finite samples, leading to further bias in the first stage estimator of ψ₁ in regular settings. This point has been demonstrated in the empirical studies of Chakraborty et al. (2010). Second, and more importantly, these shrinkage functional estimators may not possess the oracle property that with probability tending to one, the set ${ℳ}_{\star }=\{i:|{\psi }_{20}^T{S}_{2i(2)}|>0\}$ can be correctly identified and the resulting estimator performs as well as the estimator that knows the true set ℳ_⋆ in advance.

3. Inference Based on Penalized Q-Learning

3.1. Estimation Procedure

To describe our method, we still focus on the two-stage setting as given in Section 2.2 and use the same notation. As a backward recursive reinforcement learning procedure, our method follows the three steps of the usual Q-learning method, except that it replaces Step 1 of the standard Q-learning procedure with

• Step 1_p. Instead of minimizing the summed squared differences between R₂ and Q₂(S₂, A₂; β₂, ψ₂), we minimize the following penalized objective function

  $$W_2({\theta }_2)=\sum _{i=1}^n{\{R_{2i}-Q_2(S_{2i},A_{2i};{\beta }_2,{\psi }_2)\}}^2+\sum _{i=1}^n{p}_{{\lambda }_n}(|{\psi }_2^T{S}_{2i(2)}|),$$ (3.1)

  where p_λn(·) is a pre-specified penalty function and λ_n is a tuning parameter.

Because of this penalized estimation, we call our approach penalized Q-learning. Since the penalty is put on each individual, we also call Step 1_p individual selection.

Using individual selection enjoys similar shrinkage advantages as do penalized methods described by Frank and Friedman (1993), Tibshirani (1996), Fan and Li (2001), Candes and Tao (2007), Zou (2006) and Zou and Li (2008). In variable selection problems where the selection of interest consists of the important variables with nonzero coefficients, using appropriate penalties can shrink the small estimated coefficients to zero to enable the desired selection. In the individual selection done in the first step of the proposed penalized Q-learning approach, penalized estimation allows us simultaneously to estimate the second-stage parameters θ₂ and select individuals whose value functions are not affected by treatments, i.e., those individuals whose true values of ${\psi }_2^T{S}_{2(2)}$ are zero.

The above fact is extremely useful in making correct inference in the subsequent steps of the penalized Q-learning. To understand why, recall that statistical inference in the usual Q-learning is mainly challenged by difficulties in obtaining the correct asymptotic distribution of $n^{1/2}(|{\widehat{\psi }}_2^T{S}_{2(2)}|-|{\psi }_{20}^T{S}_{2(2)}|),$ Where ψ̂₂ is an estimator for ψ₂₀. Via our penalized Q-learning method, we can identify individuals whose ${\widehat{\psi }}_2^T{S}_{2(2)}={\psi }_{20}^T{S}_{2(2)}$ takes value zero; moreover, we know that for all individuals, ${\widehat{\psi }}_2^T{S}_{2(2)}$ has the same sign as ${\psi }_{20}^T{S}_{2(2)}$ asymptotically. In this case, $n^{1/2}(|{\widehat{\psi }}_2^T{S}_{2(2)}|-|{\psi }_{20}^T{S}_{2(2)}|)$ is equivalent to

$$n^{1/2}{({\widehat{\psi }}_2-{\psi }_{20})}^T{S}_{2(2)}\text{sgn}({\psi }_{20}^T{S}_{2(2)}).$$

Hence, correct inference can be obtained following standard arguments. More rigorous details will be given in Section 3.3.

The choice of the penalty function p_λn(·) can be taken to be the same as used in many popular variable selection methods. Specifically, we require p_λn(·) to possess the following properties:

• A1. For non-zero fixed θ, lim_n→∞ n^1/2p_λn(|θ|) = 0, ${lim}_{n\to \infty }{n}^{1/2}{p}_{{\lambda }_n}^{\prime }(|\theta |)=0$, and lim_n→∞ p^″ _λn(|θ|) = 0.

• A2. For any M > 0, inf_{|θ|≤M n^{−1/2 pλn}}(|θ|) → ∞, as n → ∞

Among penalty functions satisfying A1 and A2 are the smoothly clipped absolute deviation penalty (Fan and Li, 2001) and the adaptive lasso penalty (Zou, 2006), where p_λn (θ) = λ_nθ/|θ⁽⁰⁾|^ϕ with ϕ > 0 and θ⁽⁰⁾ a root-n consistent estimator of θ. To achieve both sparsity and oracle properties, the tuning parameter λ_n in these examples should be taken correspondingly. The adaptive lasso method will be implemented in this paper, where λ_n can be taken as scalars satisfying n^1/2λ_n → 0 and nλ_n → ∞, as n → ∞.

3.2. Implementation

The minimization in Step 1_p of the penalized Q-learning procedure has some unique features which distinguish it from the optimization done in the variable selection literature. First, the component to be shrunk, ${\psi }_2^T{S}_{2i(2)}$ is subject-specific; second, this component is a hyperplane in the parameter space, i.e, a linear combination of the parameters.

To deal with these issues, in this section, we propose an algorithm for the minimizing problem of (3.1) based on local quadratic approximation. Following Fan and Li (2001), we first calculate an initial estimator ψ̂₂(0) via the standard least squares estimation. We then obtain the following local quadratic approximation to the penalty terms in (3.1):

$$p_{{\lambda }_n}(|{\psi }_2^T{S}_{2i(2)}|)\approx p_{{\lambda }_n}(|{\widehat{\psi }}_{2(0)}^T{S}_{2i(2)}|)+\frac{1}{2}\frac{p_{{\lambda }_n}^{\prime }(|{\widehat{\psi }}_{2(0)}^T{S}_{2i(2)}|)}{|{\widehat{\psi }}_{2(0)}^T{S}_{2i(2)}|}\{{({\psi }_2^T{S}_{2i(2)})}^2-{({\widehat{\psi }}_{2(0)}^T{S}_{2i(2)})}^2\}$$

for ψ₂ close to ψ̂₂₍₀₎. Thus, (3.1) can be locally approximated up to a constant by

$$\sum _{i=1}^n{\{Y_{2i}-Q_2(S_{2i},A_{2i};{\beta }_2,{\psi }_2)\}}^2+\frac{1}{2}\sum _{i=1}^n\frac{p_{{\lambda }_n}^{\prime }(|{\widehat{\psi }}_{2(0)}^T{S}_{2i(2)}|)}{|{\widehat{\psi }}_{2(0)}^T{S}_{2i(2)}|}{({\psi }_2^T{S}_{2i(2)})}^2.$$ (3.2)

The updated estimators for ψ₂ and β₂ can be obtained by minimizing the above approximation. When Q(·) is (3.2), this minimization problem has closed form solution

$${\widehat{\psi }}_2={[X_{22}^T\{I-X_{21}{(X_{21}^T{X}_{21})}^{-1}{X}_{21}^T+D\}{X}_{22}]}^{-1}{X}_{22}^T\{I-X_{21}{(X_{21}^T{X}_{21})}^{-1}{X}_{21}^T\}{Y}_2,\text{and}{\widehat{\beta }}_2={(X_{21}^T{X}_{21})}^{-1}{X}_{21}^T(Y_2-X_{22}{\widehat{\psi }}_2),$$

where X₂₂ is a matrix with i-th row equal to $S_{2i(2)}^T{A}_{2i},$ X₂₁ is a matrix with i-th row equal to $S_{2i(1)}^T,$ I is the n × n identity matrix and D is an n × n diagonal matrix with $D_{ii}=\frac{1}{2}{p}_{{\lambda }_n}^{\prime }(|{\widehat{\psi }}_{2(0)}^T{S}_{2i(2)}|)/|{\widehat{\psi }}_{2(0)}^T{S}_{2i(2)}|$.

The above minimization procedure can be continued until convergence. However, as discussed in Fan and Li (2001), either the one-step or k-step estimator will be as efficient as the fully iterative method as long as the initial estimators are consistent. Since in practice, the local quadratic approximation algorithm shrinks $|{\widehat{\psi }}_2^T{S}_{2i(2)}|$ to a very small value instead of exactly zero even if the true value is zero, we will set $|{\widehat{\psi }}_2^T{S}_{2i(2)}|=0$ once the value is below a pre-specified tolerance threshold.

The choice of local quadratic approximation is mainly for convenience in solving the penalized least squares estimation in (3.1). If least absolute deviation estimation or some other quantile regression approach is used in place of least squares, then the local linear approximation of the penalty function described in Zou and Li (2008) can be used instead of local quadratic approximation, and the resulting minimization problem can be solved by linear programming.

We will use five-fold cross-validation to choose the tuning parameter, where we partition data into five folds, perform the estimation on four folds, and validate the least squares fitting on the other fold. We set ϕ = 2 as the parameter used in adaptive lasso. We acknowledge the insufficient theory support for using this method. The general guideline for choosing tuning parameters and ϕ is of great research interest but it is beyond the scope of the current paper.

3.3. Asymptotic Results

In this section, we establish the asymptotic properties for the parameter estimators in our penalized Q-learning method. We assume that the penalty function p_λn (x) satisfies A1 and A2 and that the following conditions hold

• B1. The support of S₂₍₂₎ contains a finite number of vectors, say, v₁, …, v_K. Moreover, ${\psi }_{20}^T{v}_k\ne 0$ for k ≤ K₁ and ${\psi }_{20}^T{v}_k=0$ for k ≤ K₁. Let n_k = #|{i : S_2i(2) = v_k, i = 1,…,n}|, where for a set A, #|A| is defined as its cardinality.

• B2. The true value for ${\theta }_2,{\theta }_{20}={({\psi }_{20}^T,{\beta }_{20}^T)}^T$, minimizes

  $$\underset{n}{lim}\sum _{i=1}^n{n}^{-1}{\{R_{2i}-Q_2(S_{2i},A_{2i};{\beta }_2,{\psi }_2)\}}^2;$$
  while, the true value for ${\theta }_1,{\theta }_{10}={({\psi }_{10}^T,{\beta }_{10}^T)}^T$, minimizes

  $$\underset{n}{lim}{n}^{-1}\sum _{i=1}^n{\{R_{1i}+\underset{a\in \{-1,1\}}{max}{Q}_2(S_{2i},a;{\beta }_{20},{\psi }_{20})-Q_1(S_{1i},A_{1i};{\beta }_1,{\psi }_1)\}}^2.$$

  In both expressions and in the following, we always assume that the limits exist.

• B3. For t = 1, 2, with probability one, Q_t(S_t, A_t; θ_t) is twice-continuously differentiable with respect to θ_t in a neighborhood of θ_t0 and moreover, the Hessian matrices of the two limiting functions in B2 are continuous and their values at θ_t = θ_t0, denoted I_t0, are nonsingular.

• B4. With probability one, n_k/n = p_k + O_p(n^−1/2) for some constant p_k in [0, 1].

Condition B2 says that θ₁₀ and θ₂₀ are the target values in the dynamic treatment regimens. Condition B3 can be verified via the design matrix in the two-stage setting: if Q_t takes the form of (3.2), this condition is equivalent to linear independence of [S_t(1), S_t(2)A_t] with positive probability. We note that the numerical performance for data from population with a very small probability of linear independence is likely to be unstable with small sample sizes.

Under these conditions, our first theorem shows that in Step 1_p of the penalized Q-learning procedure, there exists a consistent estimator for θ₂.

Theorem 1

Under conditions A1−A2 and B1−B4, there exists a local minimizer θ̂₂ of W₂(θ₂) such that ‖θ̂₂−θ₂₀‖ = O_P(n^−1/2+a_n), where $a_n={max}_{k=1}^{K_1}\{p_{{\lambda }_n}^{\prime }(|{\psi }_{20}^T{v}_k|)\}$.

According to the properties of p_λn(·), we immediately conclude that θ̂₂ is n^1/2-consistent. From Theorem 1, we further obtain the following result, which verifies the oracle property of the penalized method:

Theorem 2

Define the set ${ℳ}_{\ast }^c=\{i:i=1,\dots ,n,{\psi }_{20}^T{S}_{2i(2)}=0\}$. Then under conditions A1−A2 and B1−B4, ${lim}_{n\to \infty }\text{Pr}({\widehat{\psi }}_{20}^T{S}_{2i(2)}=0$, for any $i\in {ℳ}_{\ast }^c)=1$.

The set ${ℳ}_{\ast }^c$ consists of those individuals whose true value functions at the second stage have no effect from treatment. Thus Theorem 2 states that with probability tending to one, we can identify these individuals in ${ℳ}_{\ast }^c.$ We also need the asymptotic distribution of θ̂₂ in order to make inference.

Theorem 3

Under conditions A1−A2 and B1−B4, n^1/2(I₂₀ + Σ){θ̂₂ − θ₂₀ + (I₂₀ + Σ)⁻¹b} converges in distribution to N(0, I₂₀), where $b={(0_p^T,\sum _{k=1}^{K_1}{p}_k{P}_{{\lambda }_n}^{\prime }(|{\psi }_{20}^T{v}_k|)\mathit{\text{sgn}}({\psi }_{20}^T{v}_k)v_k)}^T$, and $\sum =\mathit{\text{diag}}\{0_{p\times p},\sum _{k=1}^{K_1}{p}_k{P}_{{\lambda }_n}^{″}(|{\psi }_{20}^T{v}_k|)v_k{v}_k^T\}$.

Using the results from Theorems 1–3, we are able to establish the asymptotic normality of the first stage estimator θ̂₁:

Theorem 4

Under conditions A1–A2 and B1–B4, let ${\overline{S}}_{1i}={(S_{1i(1)}^T,S_{1i(2)}^T{A}_{1i})}^T$ and ${\overline{S}}_{2i}={(S_{2i(1)}^T,S_{2i(2)}^T\mathit{\text{sgn}}({\psi }_{20}^T{S}_{2i(2)}))}^T$. Then n^1/2(θ̂₁−θ₁₀) converges in distribution to $I_{10}^{-1}\mathcal{G}$, where $\mathcal{G}\sim N[0,cov\{F_1({\theta }_{10})+{lim}_{n}1/n{\sum }_{i=1}^n{\overline{S}}_{1i}{\overline{S}}_{2i}^T{F}_2({\theta }_{20})\}]$, with F₁(θ₁₀) = ∇_θ1 Q₁(S₁, A₁;θ₁₀){Y₁ − Q₁(S₁, A₁;θ₁₀)}, F₁(θ₂₀) = (I₂₀ + Σ)⁻¹∇_θ2 Q₂(S₂, A₂;θ₂₀)(R₂ − Q₂(S₂, A₂;θ₂₀)) and cov represents the variance-covariance matrix.

3.4.Variance Estimation

The standard errors can be obtained directly since we are estimating parameters and selecting individuals simultaneously. A sandwich type plug-in estimator can be used as the variance estimator for θ̂₂:

$$\widehat{cov}({\widehat{\theta }}_2)={({\widehat{I}}_{20}+\widehat{\sum })}^{-1}{\widehat{I}}_{20}{({\widehat{I}}_{20}+\widehat{\sum })}^{-1},$$

where ${\widehat{I}}_{20}=n^{-1}{\sum }_{i=1}^n[{\nabla }_{{\theta }_2{\theta }_2}^2{\{R_2-Q_2(S_{2i},A_{2i};{\theta }_2)\}}^2]$ is the empirical Hessian matrix and $\widehat{\sum }=\text{diag}\{0_{p\times p},n^{-1}{\sum }_{i=1}^n{p}_{{\lambda }_n}^{″}(|{\widehat{\psi }}_2^T{S}_{2i(2)}|)S_{2i(2)}{S}_{2i(2)}^T\}$. As Σ̂ converges to zero as n goes to infinity, hence often negligible, we use

$$\widehat{cov}({\widehat{\theta }}_2)={\widehat{I}}_{20}^{-1}$$ (3.3)

instead, and this performs well in practice. The estimated variance for θ̂₁ is then

$$\widehat{cov}({\widehat{\theta }}_1)={\widehat{I}}_{10}^{-1}\widehat{cov}\{F_1({\widehat{\theta }}_1)+n^{-1}\sum _{i=1}^n{\overline{S}}_{1i}{\overline{S}}_{2i}^T{\widehat{F}}_2({\widehat{\theta }}_2)\},$$ (3.4)

Where Î₁₀ is the empirical estimator for I₁₀ and F̂₂(θ̂₂) = (Î₂₀ + Σ̂)⁻¹∇_θ2Q₂(S₂, A₂;θ̂₂){R₂−Q₂(S₂, A₂;θ̂₂)}. These variance estimators have good accuracy for moderate sample sizes; see section 4. This success of direct inference for the estimated parameters makes inference for optimal dynamic treatment regimens possible in the multi-stage setting.

4. Numerical Studies

We first apply the proposed method to the same simulation study conditions as designed in Chakraborty et al. (2010). A total of 500 subjects are generated for each dataset. We set R₁ = 0 and (O₁, A₁, O₂, A₂, R₂) is collected on each subject, where (O_t, A_t) denotes the covariates and treatment status at stage t (t = 1, 2). The binary covariates O_t's and the binary treatments A_t's are generated as follows:

$$\text{Pr}(O_1=1)=P(O_1=-1)=1/2,$$

$$\text{Pr}(A_t=1)=P(A_t=-1)=1/2,t=1,2,$$

$$\text{Pr}(O_2=1|O_1,A_1)=1-\text{Pr}(O_2=-1|O_1,A_1)=\mathit{\text{expit}}({\delta }_1{O}_1+{\delta }_2{A}_1),$$

where expit(x) = exp(x)/{1 + exp(x)}.

$$R_2={\gamma }_1+{\gamma }_2{O}_1+{\gamma }_3{A}_1+{\gamma }_4{O}_1{A}_1+{\gamma }_5{A}_2+{\gamma }_6{O}_2{A}_2+{\gamma }_7{A}_1{A}_2+\epsilon ,$$

where ε ∼ N(0, 1). Under this setting, the true Q-functions for time t = 1, 2 are

$$Q_2(S_2,A_2;{\beta }_2,{\psi }_2)={\beta }_{21}+{\beta }_{22}{O}_1+{\beta }_{23}{A}_1+{\beta }_{24}{O}_1{A}_1+{\psi }_{21}{A}_2+{\psi }_{22}{O}_2{A}_2+{\psi }_{23}{A}_1{A}_2,$$ (4.1)

$$Q_1(S_1,A_1;{\beta }_1,{\psi }_1)={\beta }_{11}+{\beta }_{12}{O}_1+{\psi }_{11}{A}_1+{\psi }_{12}{O}_1{A}_1.$$ (4.2)

The true values ${\beta }_{11}^0,{\beta }_{12}^0,{\psi }_{11}^0$ and ${\psi }_{12}^0$ are

$$\begin{array}{c}{\beta }_{11}^0={\gamma }_1+q_1|f_1|+q_2|f_2|+(0.5-q_1)|f_3|+(0.5-q_2)|f_4|,\\ {\beta }_{12}^0={\gamma }_2+q_1^{\prime }|f_1|+q_2^{\prime }|f_2|-q_1^{\prime }|f_3|-q_2^{\prime }|f_4|,\\ {\psi }_{11}^0={\gamma }_3+q_1|f_1|-q_2|f_2|+(0.5-q_1)|f_3|-(0.5-q_2)|f_4|,\\ {\psi }_{12}^0={\gamma }_4+q_1^{\prime }|f_1|-q_2^{\prime }|f_2|-q_1^{\prime }|f_3|+q_2^{\prime }|f_4|,\end{array}$$ (4.3)

where q₁ = 0.25(expit(δ₁ + δ₂) + expit(−δ₁ + δ₂)), q₂ = 0.25(expit(δ₁ − δ₂) + expit(−δ₁ − δ₂)), $q_1^{\prime }=0.25(\text{expit}({\delta }_1+{\delta }_2)-\text{expit}(-{\delta }_1+{\delta }_2)),q_2^{\prime }=0.25(\text{expit}({\delta }_1-{\delta }_2)-\text{expit}(-{\delta }_1-{\delta }_2))$, f₁ = γ₅ + γ₆ + γ₇, f₂ = γ₅ + γ₆ − γ₇, f₃ = γ₅ − γ₆ + γ₇, f₄ = γ₅ − γ₆ − γ₇. Let γ = (γ₁, …, γ₇)^T. We consider six settings, with values of ${\psi }_{20}^T{S}_{2(2)}$ and γ for each setting listed in Table 4.1.

Table 4.1.

Values of the linear combination ${\psi }_{20}^T{S}_{2\left(2\right)}$ in the six simulation settings. In Setting 1, γ = (0, 0, 0, 0, 0, 0, 0)^T, δ₁ = δ₂ = 0.5. In Setting 2, γ = (0, 0, 0, 0, 0.01, 0, 0)^T, δ₁ = δ₂= 0.5. In Setting 3, γ = (0, 0, − 0.5, 0, 0.5, 0, 0.5)^T, δ₁ = δ₂ = 0.5. In Setting 4, γ = (0, 0, −0.5, 0, 0.5, 0, 0.49)^T, δ₁ = δ₂ = 0.5. In Setting 5, γ = (0, 0, −0.5, 0, 1, 0.5, 0.5)^T, δ₁ = 1, δ₂ = 0. In Setting 6, γ = (0, 0, −0.5, 0, 0.25, 0.5, 0.5)^T, δ₁ = δ₂ = 0.1.

S2(2) = (1, O2, A1)T
Setting	(1,1,1)	(1,1,-1)	(1,-1,1)	(1,-1,-1)
1	0	0	0	0
2	0.01	0.01	0.01	0.01
3	1	0	1	0
4	0.99	0.01	0.99	0.01
5	2	1	1	0
6	1.25	0.25	0.25	−0.75

We applied penalized Q-learning with adaptive lasso to these six settings. The one-step local quadratic approximation algorithm is used with least squares estimation for the initial values. The tuning parameter λ in the adaptive lasso penalty is chosen by five-fold cross-validation. We take ϕ = 2 as the parameter in the adaptive least absolute shrinkage and selection operator penalty. When the estimated value $|{\widehat{\psi }}_2^T{S}_{2(2)}|<0.001$, it will be set as zero in the stage-1 estimation. The simulation results shown in Tables 4.2 and 4.3 were summarized over 2000 replications. We included the oracle estimator which knows in advance the true set ${ℳ}_{\ast }=\{i:|{\psi }_{20}^T{S}_{2(2)}|>0\}$, the hard max estimator and the soft-threshold estimator for comparison. Theoretical standard errors for the hard max estimator and the soft-threshold estimator are not available. Results on average length of the Confidence Intervals are presented in the Web Appendix.

Table 4.2.

Summary statistics and empirical coverage probability of 95% nominal percentile confidence intervals for ${\beta }_{11}^0$ and ${\beta }_{12}^0$ using the oracle estimator, the proposed penalized Q-learning based estimator, the hard max estimator and the soft-threshold estimator. “PQ” refers to the penalized Q-learning based estimator, “HM” refers to the hard max estimator, “MSE” refers to the mean squares error, “Std” refers to the average of the 2000 standard error estimates and “CP” refers to the empirical coverage probability of 95% nominal percentile confidence interval. A “*” indicates a significantly different coverage rate from the nominal rate.

	β11				β12
	bias(×1000)	MSE(×1000)	std(×100)	CP	bias(×1000)	MSE(×1000)	std(×100)	CP
Setting 1
Oracle	1	2.0	4.5	94.7	1	2.0	4.5	94.9
PQ	1	2.0	4.5	94.7	1	2.0	4.5	94.9
HM	61	6.6	–	88.7*	1	2.1	–	95.2
ST	7	2.3	–	96.2*	−1	2.0	–	94.9
Setting 2
Oracle	52	5.5	6.2	90.0*	1	2.1	4.6	95.3
PQ	−9	2.1	4.5	94.7	1	2.0	4.5	94.8
HM	52	5.5	–	90.8*	1	2.1	–	95.1
ST	−3	2.2	–	94.8	−1	2.0	–	95.1
Setting 3
Oracle	0	3.0	5.5	94.6	1	2.0	4.5	95.1
PQ	0	3.1	5.5	94.2	2	2.0	4.5	95.2
HM	30	4.3	–	93.0*	2	2.1	–	95.2
ST	−5	3.3	–	93.5*	−1	2.1	–	94.9
Setting 4
Oracle	26	4.0	6.2	93.8*	2	2.1	4.6	95.2
PQ	−5	3.1	5.5	94.3	2	2.0	4.5	95.1
HM	26	4.0	–	93.4*	2	2.1	–	95.1
ST	−10	3.4	–	93.5*	−1	2.1	–	95.0
Setting 5
Oracle	0	3.8	6.1	94.7	2	2.7	5.2	95.1
PQ	−2	3.8	6.1	94.4	0	2.7	5.2	95.0
HM	15	4.1	–	94.1	−5	2.7	–	94.3
ST	−8	4.0	–	94.9	−3	2.8	–	94.9
Setting 6
Oracle	2	3.8	6.2	94.8	−1	2.3	4.8	94.7
PQ	1	3.8	6.2	94.7	−1	2.3	4.8	94.7
HM	2	3.8	–	94.3	−1	2.3	–	95.2
ST	45	6.3	–	87.2*	−1	2.3	–	95.2

Table 4.3.

Summary statistics and empirical coverage probability of 95% nominal percentile confidence intervals for ${\psi }_{11}^0$ and ${\psi }_{12}^0$ using the oracle estimator, the proposed penalized Q-learning based estimator, the hard max estimator and the soft-threshold estimator. The notations are the same as in Table 2.

	ψ11				ψ12
	bias ×1000	MSE×1000	std×100	CP	bias×1000	MSE×1000	std×100	CP
Setting 1
Oracle	−1	1.9	4.5	95.3	0	2.0	4.5	94.7
PQ	−1	1.9	4.5	95.3	0	2.0	4.5	94.7
HM	0	2.4	–	93.7*	−1	2.1	–	94.5
ST	1	2.3	–	94.8	−1	2.1	–	94.6
Setting 2
Oracle	0	2.5	5.8	97.3*	−1	2.1	4.6	95.0
PQ	−1	1.9	4.5	95.3	0	2.0	4.5	94.8
HM	0	2.5	–	94.8	−1	2.1	–	94.4
ST	1	2.3	–	94.8	0	2.1	–	94.4
Setting 3
Oracle	−1	2.9	5.5	95.0	0	2.0	4.5	94.8
PQ	−10	3.1	5.5	94.0	−1	2.0	4.5	94.6
HM	−31	4.2	–	93.8*	−1	2.1	–	94.0
ST	−11	4.0	–	95.0	0	2.1	–	94.0
Setting 4
Oracle	−26	4.0	6.2	94.9	−1	2.1	4.5	95.0
PQ	−6	3.1	5.5	94.6	0	2.0	4.5	94.6
HM	−26	4.0	–	94.5	−1	2.1	–	94.0
ST	−7	3.4	–	95.1	0	2.1	–	93.9
Setting 5
Oracle	−1	3.5	6.1	95.8	−1	2.5	4.9	94.3
PQ	−5	3.6	6.1	95.2	0	2.5	4.9	94.3
HM	−16	4.0	–	94.6	6	2.6	–	94.0
ST	−3	4.0	–	95.2	−3	2.6	–	94.2
Setting 6
Oracle	2	3.9	6.2	95.0	0	2.4	4.8	94.2
PQ	2	4.0	6.2	94.6	0	2.4	4.8	94.2
HM	2	3.9	–	93.7*	0	2.4	–	94.1
ST	1	4.6	–	91.4*	2	2.5	–	94.1

The true values ${\beta }_{11}^0,{\beta }_{12}^0,{\psi }_{11}^0$ and ${\psi }_{12}^0$ of stage-1 parameters are linear combinations of four absolute value functions |f₁|, |f₂|, |f₃|, and |f₄| from (4.3). It can be shown by definition that, with a bias of order o(n^−1/2), the hard max estimators of stage-1 parameters are linear combinations of four corresponding absolute value functions, with stage-2 estimators instead of true values to plug into |f₁|, |f₂|, |f₃|, and |f₄|. Therefore the performances of the hard max estimators are greatly affected by the estimation of each of the four absolute value functions. Furthermore, the bias of the hard max estimators mainly come from that of estimating four absolute value functions. We now discuss the performance of our estimator, hard max estimator and the oracle estimator in these six settings.

Setting 1 is a setting where there is no second-stage treatment effect, as ${\psi }_{20}^T{S}_{2(2)}=0$ for all values of S₂₍₂₎. The hard-max estimator will incur asymptotic biases for all the four terms |f₁|, |f₂|, |f₃| and |f₄|, all four at about the same order of $\sqrt{2/(n\pi )}=0.036$, as in this case ${\{|f_i|\}}_{i=1}^4=0$. As shown in (13), the biases in the estimation of |f₁|, |f₂|, |f₃| and |f₄| will be almost completely canceled out in the estimation of ${\beta }_{12}^0,$ and ${\psi }_{12}^0,$ due to the fact that the sum of the coefficients are zero. These biases of estimating |f₁|, |f₂|, |f₃| and |f₄| are largely canceled out in the estimation of ${\psi }_{11}^0,$ as the sum of the coefficients are close to zero. The hard-max estimator of ${\beta }_{11}^0$ has a significant bias because the coefficients of the four absolute value terms, q₁, q₂, 0.5 − q₁ and 0.5 − q₂, are all positive and sum to 1.

The simulation results of Setting 1 are consistent with the theoretical observations in terms of the hard-max estimation. The oracle estimator automatically sets the estimator of ψ₂ to be zero. It has no significant bias, with standard errors accurately predicted by the theory and 95% confidence interval coverage close to the nominal value. The penalized Q-learning based estimator's performance is actually identical to the oracle estimator. The hard-max estimator has a significant bias and inferior mean square error in β̂₁₁ while remaining consistent for estimation of the other three stage-1 parameters.

Setting 2 is regular but very close to Setting 1 with ${\psi }_{20}^T{S}_{2(2)}$ all equal to 0.01 for all values of S₂₍₂₎. The hard-max estimator's performance is very similar to setting 1. Its 95% confidence interval shows poor coverage for ${\beta }_{11}^0$ and ${\psi }_{11}^0$. As the value of ${\psi }_{20}^T{S}_{2(2)}$ is nonzero, the oracle estimator reduces to the hard-max in this setting. Although the penalized Q-learning based estimator demonstrates a small bias (-0.009) in the estimation of ${\beta }_{11}^0,$ the bias is less than one fifth of that of the oracle estimator and the mean square error is less than half of the oracle estimator. Its standard error estimate remains close to the empirical values.

Setting 3 is another setting where there is no second-stage treatment effect. Setting 3 is another setting where there is no second-stage treatment effect for a positive proportion of subjects in the population. The value of ${\psi }_{20}^T{S}_{2(2)}$ is equal to 0 when A₁ = −1 with probability one half. The hard-max estimator incurs bias on the order of O(n^−1/2) in the estimation of |f₂| and |f₄|, but not |f₁| and |f₃|, as f₂ = f₄ = 0 and f₁ = f₃ = 1. As seen from (13), the hard-max estimation of ${\beta }_{12}^0,$ and ${\psi }_{12}^0,$ is still approximately unbiased, due to the canceling-out of the coefficients of the four absolute value terms. The estimation of ${\beta }_{11}^0,$ is biased from the true value at approximately half of the bias of Setting 1, due to the values of the |f_i|'s and their coefficients. The estimation of ${\psi }_{11}^0,$ is also biased, with similar magnitude of bias as in β̂₁₁ but with reversed sign. The simulation study exactly confirms the theoretical observations of the hard-max estimator. The oracle estimator has no statistically significant bias and its standard error is precisely predicted by the theoretical calculation. The penalized Q-learning based estimator has a bias in ψ̂₁₁ but the bias is still three times smaller than that of the hard-max estimator. Otherwise, the penalized Q-learning based estimator has almost exactly the same performance as the oracle estimator.

Setting 4 is a regular setting but very close to Setting 3. The hard-max estimator's performance is similar to Setting 3. The oracle estimator reduces to the hard-max estimator. The penalized Q-learning based estimator outperforms the oracle estimator, with both a smaller bias (5 times smaller), and a correctly predicted standard error. This phenomena is consistent with findings in Setting 2.

In Setting 5, the term ${\psi }_{20}^T{S}_{2(2)}$ is equal to zero when (O₂, A₁) = (−1, −1) with probability one fourth. The hard-max estimator will incur bias in the estimation of |f₄|, since f₄ = 0. Consequently, all the four stage-1 parameter estimators will be biased. The bias in β̂₁₁ will be approximately a quarter of that in Setting 1. The bias in β̂₁₂ is about half of that of β̂₁₁ with reversed sign. The bias in ψ̂₁₁ is about the same magnitude as that of β̂₁₁ with reversed sign. The bias in ψ̂₁₂ is about half of that of β̂₁₁. In this setting, the oracle estimator has the best performance, with no significant bias and well predicted standard errors. The penalized Q-learning based estimator has a bias in ψ̂₁₁ but the bias is much smaller than the hard-max estimator. The penalized Q-learning based estimator has no noticeable bias in the other three parameter estimations and the standard error calculations are accurate when compared to Monte-Carlo errors.

Setting 6 is a completely regular setting with values of ${\psi }_{20}^T{S}_{2(2)}$ well above zero. The penalized Q-learning based estimator has almost identical performance as the oracle estimator, which is the same as the hard-max estimator. Both estimators are unbiased with accurately calculated standard errors.

In summary, the behavior of the PQ-estimator, including its bias, mean square error, theoretically computed standard error and coverage probability of theoretically computed 95% confidence intervals, are consistent in all six settings.

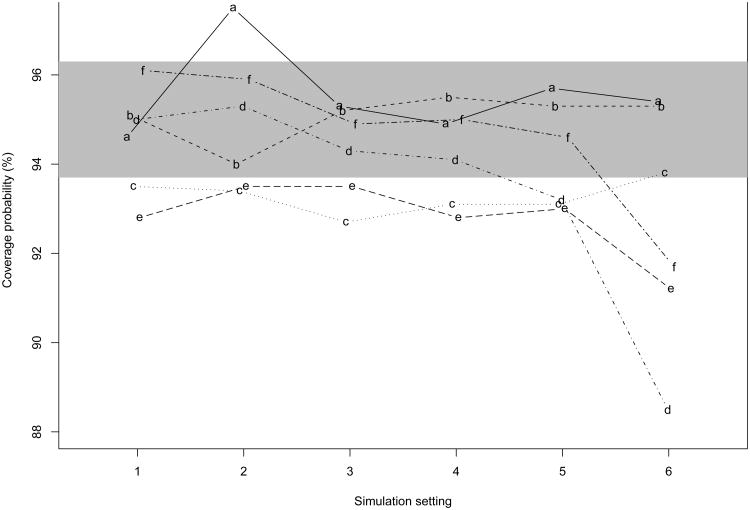
Chakraborty et al. (2010) proposed several bootstrapped confidence intervals for the hard max estimator as well as hard-threshold estimators with α in Step 2 set to be 0.08 or 0.20 and the soft-threshold estimator. In order to compare the confidence intervals from the proposed penalized Q-learning based estimator with these bootstrapped methods, we re-ran the simulations with the penalized Q-learning based estimator with sample size n = 300 and 1000 replications. The coverage probabilities from different inferential methods in the six settings are compared in Figure 1, where the results from the hard max, hard threshold and soft threshold methods based on hybrid bootstrapping for variance estimation are shown. Overall, the competing methods cannot provide consistent coverage rates across all six settings while our penalized Q-learning based method always gives coverage probabilities that are not significantly different from the nominal level.

Fig. 1.

Plot of 95% confidence interval's coverage rates with several inference methods in six simulation settings. The shaded area indicates coverage rates considered to be nonsignificantly different from nominal rate 0.95. Curve “a”: the coverage probabilities from the oracle estimator; curve “b”: the coverage probabilities from the penalized Q-learning method; curve “c”: the coverage probabilities from the hard-max estimator; curve “d”: the coverage probabilities from the hard-threshold estimator with α = 0.08; curve “e”: the coverage probabilities from the hard-threshold estimator with α = 0.2; curve “f”: the coverage probabilities from the soft-threshold estimator. Curves “c”–“f” all use hybrid bootstrapping.

We also apply percentile bootstrapping or double bootstrapping variance estimation in the other competing methods and find that the hard max estimator with the double bootstrapped confidence interval and the soft-threshold estimator with the percentile bootstrapped can give reasonable coverage probabilities. Nonetheless, the penalized Q-learning based estimator has a significant computational advantage over these two inference methods. In a comparison run of analyzing one dataset with sample size 300, the hard max with double bootstrap confidence interval at 500 first-stage and 100 second-stage bootstrap iterations needs 316.35 seconds. The soft thresholding with percentile confidence interval at 1000 bootstrap iterations takes 10.98 seconds. In contrast, the penalized Q-learning based estimator takes only 0.14 second.

Finally, we analyze data from the mental health study described in Fava et al. (2003) using the proposed method. The details are given in the online Supplemental Material.

5. Discussion

The proposed penalized Q-learning provides valid inference based on an approximate normal distribution for the estimators of the regression coefficients. Recently while this paper is under review, Chakraborty et al. (2013) proposed m-out-of-n bootstrap as a remedy to the non-regular inference in Q-learning. This modified bootstrap is consistent, and can be used in conjunction with the simple hard-max estimator.

Under some special cases, the proposed method is the same as variable selection but in general, it is for individual subject selection instead of individual variable selection. In small samples, our penalization on the linear predictor would possibly impose some constraints as demonstrated in the following example provided by a referee. Suppose that ψ₂ = (ε, −ε)^T and that the following four feature vectors are in the support of S₂₍₂₎: (1, 1)^T, (1, 1 + a)^T, (1 + a, 1)^T, (1 + a, 1 + a)^T for a > 0. For small value of ε and large value of a, say a = 100/ε, it is possible that the penalized estimator ψ̂₂ shrinks the entire coefficient vector to zero due to the penalty put on |ψ^TS₂₍₂₎|. Every patient is thus deemed to have no treatment effect. The true treatment effect for subject (1, 1+ a)^T and (1 + a, 1)^T, however is non-negligible.

This dilemma is due to the finite rank of the covariate space and lack of power to distinguish groups with small effects in small samples. One possibility to alleviate the dilemma is to use a penalty of the form

$$\sum _{i=1}^n\{p_{{\lambda }_n}(|S_{2i(2)}^T{\psi }_2|)+p_{{\lambda }_2}(|S_{2i(2)}^T{\psi }_2-S_{2i(2)}^T{\psi }_2^{°}|)\},$$

where ${\psi }_2^{°}$ is a consistent initial estimator of ψ₂. This penalty can shrink estimated $S_{2i(2)}^T{\psi }_2$ to zero if the truth is zero; otherwise, it will force $S_{2i(2)}^T{\psi }_2$ to be not far from $S_{2i(2)}^T{\psi }_2^{°}$.

Although the linear model form of the Q-functions presented here is an important first step, as well as being useful for illustrating the ideas of this paper, this form may not be sufficiently flexible for certain practical settings. Semiparametric models are a potentially very useful alternative in many such settings because such models involve both a parametric component which is usually easy to interpret and a nonparametric component which allows greater flexibility. Generalizations of Q-functions to allow diverse data such as ordinal outcome, censored outcome and semiparametric modeling, are thus future research topics of practical importance.

The theoretical framework is based on discrete covariates. This condition is not as restrictive as it looks. For example, in a practical two-stage setting where continuous covariates are presented, unless in the rare case where the parameter ψ₂₀ is zero, the set ${ℳ}_{\ast }^c=\{i:{\psi }_{20}^T{S}_{2i(2)}=0\}$ will not have positive probability. Having said that, we can always discretize continuous covariates, though with a loss of information. Future research to extend our work to continuous covariates would also be very useful in practice. Likewise, the framework works for two-level treatments. The generalization to multilevel treatments will be a natural and useful next step.

In many clinical studies, the state space is often of very high dimension. To develop optimal dynamic treatment regimes in this case, it will be important to develop simultaneous variable selection and individual selection. More modern machine learning techniques such as support vector regression and random forests can be nested into our penalized Q-learning framework as powerful tools to develop optimal dynamic treatment regimes.

Our method is proposed to the general setting in randomized clinical trials. It will be interesting and practically useful to develop the optimal dynamic treatment regime from the observational studies. To generalize the proposed methods to observational studies, under certain assumptions (for example, no-unobserved confounders), propensity scores weighted approach can be incorporated into the proposed PQ-learning. It is beyond the scope of the current paper and we are currently investigating this topic.