Algorithm 3.

ONEROW: Solve (11) via dual.

Inputs: ${\stackrel{\sim }{\beta }}_j^{+},{\stackrel{\sim }{\beta }}_j^{-}\in ℝ$, Θ̃j ∈ ℝp−1, λ ≥ 0. Find α̂. Define $f(\alpha )={\Vert S({\stackrel{\sim }{\mathrm{\Theta }}}_j,t(\lambda /2+\alpha ))\Vert }_1-{[{\stackrel{\sim }{\beta }}_j^{+}+t\alpha ]}_{+}-{[{\stackrel{\sim }{\beta }}_j^{-}+t\alpha ]}_{+}$. If f(0) ≤ 0, take α̂ = 0 and go to step 2. Form knot the set $\mathcal{P}={\{\mid {\stackrel{\sim }{\mathrm{\Theta }}}_{jk}\mid /t-\lambda /2\}}_{k=1}^p\cup \{-{\stackrel{\sim }{\beta }}^{\pm }/t\}$, and let 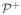= 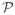∩ [0, ∞). Evaluate f(p) for p ∈ 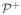. If f(p) = 0 for some p ∈ 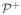, take α̂ = p and go to step 2. Find adjacent knots, p1, p2 ∈ 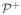, such that f(p1) > 0 > f(p2). Take $$\widehat{\alpha }=-f(p_1)[f(p_2)-f(p_1)]/(p_2-p_1).$$ Return Θ̂j = 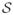[Θ̃j, t(λ/2+ α̂)] and ${\widehat{\beta }}_j^{\pm }={[{\stackrel{\sim }{\beta }}_j^{\pm }+t\widehat{\alpha }]}_{+}$.