Figure 3. Learning curves.

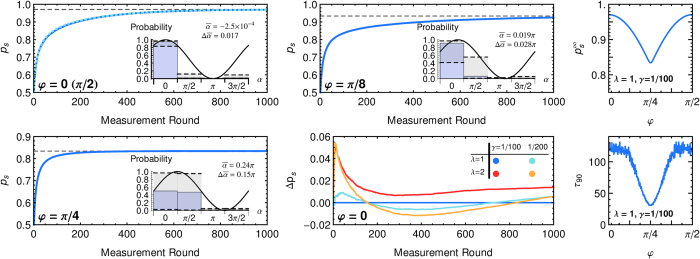
Left: The success probability p_s as a function of number of measurement rounds on the qubit in state |φ〉 is shown for four angles as averaged over an ensemble of N = 1000 agents running in parallel (λ = 1, γ = 1/100). The time scale of learning can be rescaled by increasing both λ and γ. Dashed lines give analytical approximations of the asymptotic values (see text). The insets show the transition probabilities of the average agent after 1000 learning steps, 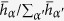, where 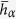is the ensemble average of the weight h_α, together with the minimal and maximal probabilities obtained in the ensemble (as error bars), and the analytical curve of p(+1|φ, α). From the transition/measurement probabilities of a single agent j we infer³⁰,³¹ its mean angle 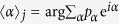. The ‘‘vector sum’’ of the mean angles of the 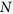individual agents is the complex number 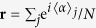, which determines the ensemble average of the mean angle 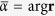and its circular standard deviation 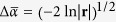. Bottom middle: A higher reward scaling λ and lower damping rate γ give a faster initial learning and a higher asymptote, with a slower final convergence for the latter. Curves show the differences of all p_s with the reference case λ = 1, γ = 1/100. Top right: Asymptotic success probability 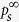(analytical approximation) as a function of φ for 4 projectors. The curve is π/2-periodic. Bottom right: Learning time τ₉₀ for the ensemble of agents to reach 90% of 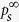. Data is the average of the learning times of 1000 agents.