Fig. 2.

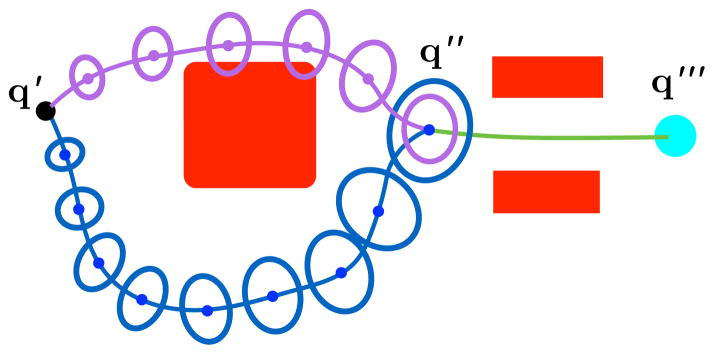
Consider two paths from configuration q′ to a configuration q‴, with ellipsoids representing uncertainty at stages along the paths. RRT* and related asymptotically optimal motion planners assume that the optimal substructure property holds, i.e., if q″ is along the optimal path from q′ to q‴, the subpath from q′ to q″ is itself an optimal path from q′ to q″. While this is true for shortest path problems, optimal substructure does not hold for some uncertainty-aware cost metrics such as maximizing probability of success. Between q′ and q″, the probability of collision for the purple path is larger than the probability of collision for the blue path due to lesser clearance from the obstacles. But the purple plan has lesser estimated uncertainty in state estimation at q″, which will lead to a smaller probability of collision when the robot passes through the narrow passage between q″ and q‴. The lack of optimal substructure when planning in configuration space makes achieving asymptotic optimality more difficult.