Fig. 2.

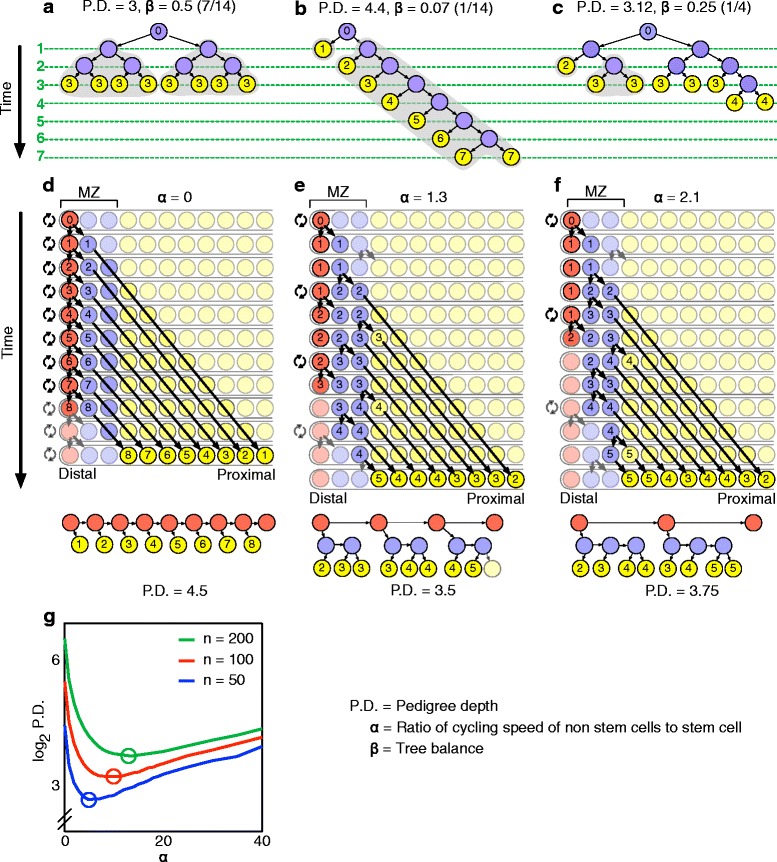
Slow-cycling stem cells allow for an advantageous tradeoff between pedigree-depth minimization and early production of differentiated cells. a Average pedigree depth (P.D.) of differentiated cells, defined as the average number of divisions between differentiated cells and the founding progenitor, is minimized by balanced trees (i.e. trees where no pair of cells at the bottom of the tree has pedigree depths that differ by more than one), but differentiated cells (yellow) are not produced until all cells have finished dividing. In this optimal configuration, P.D. = log₂(n) where the total number of cells to be produced n = 8. β is the tree balance as defined by [39] (range: 0–0.5, with 0.5 corresponding to perfect balance). The gray outline indicates sister subtrees that are the least balanced (most relevant to b and c). The time axis units are given in rounds of cell division. The individual pedigree depth of differentiated cells is shown as the inset number. b Early production of differentiated cells can be obtained by successive rounds of asymmetric divisions of a progenitor cell (blue), at the cost of a substantial increase in average pedigree depth. c Pedigree trees can be shaped to allow for early differentiated cell production without incurring a large pedigree-depth penalty. d–f Pedigree tree shape can be controlled by modulating the cycling speed of a stem cell located at the distal end of a model tubular organ. Cells are pushed out toward the proximal end as a result of proliferation, and differentiate when reaching a threshold distance from the distal end (yellow). α is the ratio of the cycling speed of non-stem cells to the cycling speed of the stem cell (the higher α, the lower the relative stem-cell cycle speed). Inset numbers show cell pedigree depth as in (a–c). d If only the stem cell cycles, the pedigree tree is similar to that in (b) and the average pedigree depth is high. e If the stem-cell cycles are ~30 % slower than other cells in the MZ, the pedigree-depth tree is more balanced. f It is not beneficial for the stem cell to cycle more slowly than in (e): pedigree depth increases as a result of the increased cycling that other cells in the MZ must undergo to produce the desired cell number. g There exists a single optimal value of α that minimizes the average pedigree depth within the context of models shown in (d–f); the optimal α increases as the total number n of cells to be produced increases (compare blue, red, and green curves). In other words, the more cells in total are to be produced, the slower stem cells should cycle to preserve the low pedigree depth