Impact of Uncertain Head Tissue Conductivity in the Optimization of Transcranial Direct Current Stimulation for an Auditory Target

Abstract

Objective

Transcranial direct current stimulation (tDCS) is a non-invasive brain stimulation technique to modify neural excitability. Using multi-array tDCS, we investigate the influence of inter-individually varying head tissue conductivity profiles on optimal electrode configurations for an auditory cortex stimulation.

Approach

In order to quantify the uncertainty of the optimal electrode configurations, multi-variate generalized Polynomial Chaos (gPC) expansions of the model solutions are used based on uncertain conductivity profiles of the compartments skin, skull, gray matter, and white matter. Stochastic measures, probability density functions, and sensitivity of the quantities of interest are investigated for each electrode and the current density at the target with the resulting stimulation protocols visualized on the head surface.

Main results

We demonstrate that the optimized stimulation protocols are only comprised of a few active electrodes, with tolerable deviations in the stimulation amplitude of the anode. However, large deviations in the order of the uncertainty in the conductivity profiles could be noted in the stimulation protocol of the compensating cathodes. Regarding these main stimulation electrodes, the stimulation protocol was most sensitive to uncertainty in skull conductivity. Finally, the probability that the current density amplitude in the auditory cortex target region is supra-threshold was below 50%.

Significance

The results suggest that an uncertain conductivity profile in computational models of tDCS can have a substantial influence on the prediction of optimal stimulation protocols for stimulation of the auditory cortex. The investigations carried out in this study present a possibility to predict the probability of providing a therapeutic effect with an optimized electrode system for future auditory clinical and experimental procedures of tDCS applications.

1. Introduction

Transcranial direct current stimulation (tDCS) is a non-invasive method, which modulates cortical excitability in the human brain [1]. The standard tDCS electrode configuration consists of two relatively large electrodes attached to the scalp, with the active electrode (anode) to be placed above the presumed target region. Computer simulation studies of the induced current flow pattern in detailed MRI-derived finite element (FE) head models demonstrated that the cortical current flow pattern is rather broad with often maximal stimulation in non-target brain regions [2, 3]. In order to overcome these limitations of standard electrode configurations, algorithm-based current flow optimization approaches using multiple electrodes have been developed [4, 5]. The aim of current flow optimization approaches is to optimize the focality, orientation, and/or intensity of current density at a target location while minimizing current density in non-target brain regions. In general, a point electrode model (PEM) is used to simulate the stimulation electrodes, i.e. they are identified by a point on the head surface. An alternative approach is to use a complete electrode model (CEM), which incorporates shunting effects and contact impedances between the electrode and the head model resulting in non-uniform current density distributions at the electrode-head-interface [6, 7, 8]. Recently performed computer simulations on tDCS have shown that main differences between CEM and PEM are situated locally around the electrodes but are only subtle in brain regions [9]. Taking into account Helmholtz reciprocity, the reported results were in agreement with a simulation study comparing PEM and CEM for source analysis and reconstruction in electroencephalography (EEG) modeling [10]. Both studies suggest that the application of PEM in the current study allows for a sufficiently accurate modeling of the current density within brain regions compared to CEM. Nevertheless, optimization procedures strongly rely on accurate and detailed MRI-derived individual head models. While a guideline for efficient yet accurate volume conductor modeling in tDCS has been presented [2], the influence of inter-individually varying conductivity profiles is rather unclear.

The electrical conductivity of the skull, skin, and brain tissue are based on experimental data and are subject to uncertainty in literature [11, 12, 13, 14]. This uncertainty arises from difficulties associated with the measuring process such as electrode polarization at low frequencies, changes in the conditions of the tissue samples postmortem, and inter-individual variations. In general, determining the influence of uncertain model parameters on the stimulation protocol utilizes stochastic methods, such as Monte Carlo simulation (MCS), which allow for the investigation of the model output statistics by computing a large number of model realizations [15]. Since the deterministic model is computationally expensive, MCS is often not practicable. To reduce the number of required model realizations, the generalized polynomial chaos technique (gPC) is applied, which determines a simply evaluable surrogate model by using the deterministic model as some kind of a “black-box”. The method was already successfully applied in previous studies regarding bio-electrical applications [16, 17] and is enhanced in this study to allow for a more accurate computation of the model output statistics based on the approach proposed in [18]. The gPC expansions of the quantities of interest can be used to compute their sensitivity on the uncertain conductivity of each brain tissue type as well as sensitivity arising out of their interactions. This global sensitivity analysis is carried out using Sobol’ indices, which describe the conditional variances of the quantities of interest [19].

This study aims at the uncertainty quantification of the optimal electrode configuration of a multiple electrode setup for auditory cortex stimulation, which will allow for an assessment of the robustness of the optimal electrode configuration. Based on the uncertainty in the conductivity of skin, skull and brain tissue, a multi-variate gPC expansion will be used to compute the stochastic measures, probability density functions, and sensitivity of the quantities of interest. These measures will allow for a recommendation on the optimal configuration of the stimulation electrodes as well as “risk margins” for the used stimulation intensities.

2. Methods

2.1. Modeling Transcranial Direct Current Stimulation

For this study, a high-resolution realistically-shaped hexahedral finite element head model of a healthy 26-year-old male subject is generated from T1- and T2-weighted magnetic resonance images [2]. Segmentation into tissue compartments skin, skull, cerebrospinal fluid (CSF), gray matter, and white matter is performed using FSL [20]. The mesh generation is carried out by using the freely-available software SimBio-VGRID ^‡ (see Wagner et al [2] for further details).

For modeling the current density vector fields, the quasi-static approximation to Maxwell’s equations is applied. This leads to a Laplace equation ∇·σ∇Φ = 0 with inhomogeneous and homogeneous Neumann boundary conditions at the electrode surfaces and at the remaining model surface, respectively [2]. This partial differential equation is referred to as the tDCS forward problem in the following. The finite element method (FEM) yields a sparse linear equation system Ku = b with K ∈ ℝ^N×N being the FE stiffness matrix, u ∈ ℝ^N being the solution vector comprising the electric potential at the discretized nodes of the volume conductor model, and b ∈ ℝ^N being the right-hand side vector with non-zero values only at the discretized boundary nodes of the electrode surfaces. Linear ansatz functions for the corresponding components u_k, k = 1, …, N of the solution vector u are used to approximate the electric potential Φ in the volume conductor model. An algebraic multigrid preconditioned conjugate gradient solver is used to solve the large sparse equation system in a geometry-adapted hexahedral FE model with approximately N = 2.2 million degrees of freedom [2]. For the solution of the equation system, we used a residual error of 10⁻⁷. The resulting current density distribution J = σ∇Φ is computed using the solution vector u.

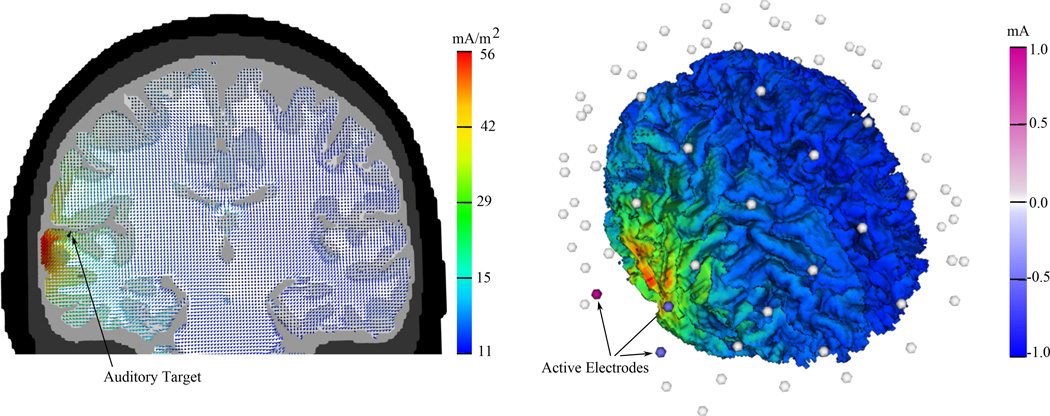
An electrode array consisting of 74 fixed electrode locations (the locations of an extended 10/10 EEG system) is used for auditory cortex stimulation. The auditory target was chosen in this study, because of its potential clinical relevance for tinnitus treatment. Experimental studies on human patients were able to demonstrate that anodal stimulation of the left temporoparietal cortex resulted in a reduction of tinnitus [21, 22]. Figure 1 shows a three electrode setup for auditory cortex stimulation with a total current of 1mA injected to the anode and two negative currents of 0.5mA injected to the cathodes. The stimulation setup has thus not been optimized.

Figure 1.

Current density for auditory cortex stimulation for a three electrode setup with a total current of 1 mA. The left Figure demonstrates current density as a vector field on a coronal slice through the head model. The auditory target vector e is indicated by a black cone. The right Figure shows the three electrode stimulation protocol and the corresponding volume rendering of the current density on the brain surface.

For the optimization of the stimulation protocols, the full multi-channel tDCS electrode array is used. In order to estimate the tDCS influence matrix A = [A₁, ⋯, A_S−1] ∈ ℝ^3N×(S−1) the first electrode is selected as a reference, resulting in 73 pairs of surface electrodes. For each pair, the boundary condition consists of a unit current applied to electrode i and a negative unit current applied to the reference electrode. The FEM yields a solution Φ_i to the tDCS forward problem and the matrix A_i = σ∇Φ_i is computed via fast Fortran routines implemented in SimBio ^§ (see [2] for further details).

2.2. Optimization Scheme

The optimized stimulation protocols are computed by using the alternating direction method of multipliers (ADMM) [23]. The constrained optimization problem is formulated by

$$\mathit{\text{minimize}}\beta {\Vert \mathit{s}\Vert }_1-{\int }_{\mathrm{\Omega }}\langle \mathbf{A}\mathit{s},\mathit{e}\rangle \mathrm{d}x$$

$$\mathit{\text{subject to}}|\mathbf{A}\mathit{s}|\le \mathit{\epsilon },$$ (1)

$${\Vert \tilde{\mathit{s}}\Vert }_1\le 4,\tilde{\mathit{s}}=\left(\begin{array}{c}\hfill \mathit{s}\hfill \\ \hfill s_{\text{ref}}\hfill \end{array}\right)$$

with s ∈ ℝ^S−1 and s_ref being the optimized stimulation protocol at the non-reference electrodes and the resulting stimulation at the reference electrode, respectively, e ∈ ℝ^3N being the target vector with non-zero entries only at the target, ε ∈ ℝ^3N with entries ε_i = 0.001 Am⁻² for i = 1, …, 3N being the threshold vector and β = 0.001. Since the product of the tDCS influence matrix A with the stimulation protocol s describes the optimized current flow field in the volume conductor model, the term ∫_Ω 〈As, e〉 dx is maximal when the induced current density distribution is parallel to the target vector e.

In order to fulfill safety of stimulation and to minimize the current density in non-target regions, the state constraint |As| ≤ ε is introduced with ε set larger in the target region than in non-target regions. Secondly, the condition ‖s̃‖₁ ≤ 4, which describes the L₁–norm of s̃, limits the total current. The total current is defined as the sum of all positive currents, applied in the stimulation protocol to 2 mA, in line with [4]. For all optimizations, the software package MATLAB^{® ‖} is used.

For appropriate estimation of the target location and orientation e, the auditory cortices of the subject are localized in combined 74-channel EEG and 274-channel MEG experiments. To localize the auditory N1 component and to obtain its orientation correctly, a source analysis of simultaneously measured auditory evoked fields (AEF) and potentials (AEP) is performed by using the following experimental setup: 350 Hz sinusoidal tones with 800 ms duration and a stimulus onset asynchrony of 3.5 – 4.5 s in order to avoid habituation, overall 120 trials, are presented. After pre-processing, a two-dipole fit (one dipole in each hemisphere) for the rising flank of the N1 component from the averaged and combined AEF and AEP is computed by using the neuroimaging software CURRY ^¶. By combining the AEF and AEP, the orientation of the auditory cortex target vector was mainly radial to the cortical surface.

2.3. Uncertainty Quantification Using Polynomial Chaos

The uncertainty in the model parameters results in an uncertainty in the quantities of interest, e.g., the optimal stimulation amplitude for each electrode. The quantification of the uncertainty in these quantities is carried out using the generalized Polynomial Chaos technique (gPC). This method expands a model output Y into a series of multi-variate orthogonal basis functions ψ(ξ):

$$Y=\sum _{i=0}^{\infty }{c}_i{\psi }_i(\mathit{\xi }).$$ (2)

The basis functions depend on the standard uniformly distributed random variables ξ = (ξ₁, …, ξ_M), which are also connected to the random model parameters X = (X₁, …, X_M) by a transformation depending on their probability distributions. For uniformly distributed random variables, the optimal choice of basis functions ψ(ξ) is formed by the product of Legendre Polynomials, whose degrees in each dimension are stored in a multi-index α⁽ⁱ⁾ [15]. The coefficients c_j depend on the response of the model output Y on the random model parameters X and can be computed by projecting the truncated equation (2) on each basis function. The resulting integral is solved using numerical integration, which requires the evaluation of the model output at a number N of quadrature nodes [24]. In general, tensor grid quadrature rules are applied, which result in an exponential growth of the required quadrature nodes with the number M of random model parameters. To reduce this “curse of dimensionality”, Smolyak sparse grids SG(L,M) can be directly applied to the integral formulation of the coefficients, which are explained in detail in previous studies where they were already used for the uncertainty quantification in the modeling of deep brain stimulation [16, 17, 25]. The sparsity of these grids depends on the underlying quadrature rule and can be increased by using nested grids where the level L determines the maximum number of nodes in each dimension to be n(l) = 2^l + 1, l = 1, …, L. This non-intrusive method integrates all coefficients exactly for basis functions satisfying the condition ‖α⁽ⁱ⁾‖₁ ≤ p with the expansion order p = L, which determines also the number of basis functions P at which (2) is truncated [16].

This strict condition is required to ensure the exclusion of aliasing errors for higher order polynomial degrees, resulting in a loss of their orthogonal property as presented in [18]. The authors of the mentioned study proposed an alternative approach, which overcomes this limitation and allows for an optimal use of the quadrature nodes to integrate higher order polynomial degrees called sparse pseudo-spectral approximation method (SPAM). Instead of directly applying the integral formulation of the coefficients to the sparse grid SG(L,M), gPC expansions (2) for each tensor-product sub-grid of the used sparse grid are computed. The algorithm, which linearly combines the sub-grids to the sparse grid formulation, is used to compute the linear combination of the previously computed gPC expansions. Therefore, SPAM allows for expansion orders p in each dimension up to an optimal degree d(p) = 2^p−1 without increasing the number of required quadrature nodes. To ensure its functionality, the implemented MATLAB version of this method was validated using several multi-variate analytical test functions based on those used in [18].

2.4. Modeling of the Tissue and Skull Conductivities

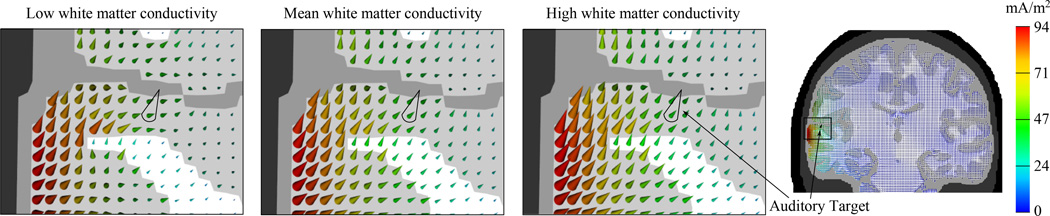
The upper and lower resistivity values for the skin, gray and white matter compartments were selected to be identical to those used in [12, Table 6.2], who used upper and lower bounds of approximately ±50% of the mean resistivity to investigate changes in neuromagnetic fields due to variations in the resistivity. The upper and lower conductivity values for the skull compartment were set to the minimum (1.6 mS m⁻¹, [26]) and maximum (33.0 mS m⁻¹, [27]) value out of 11 different conductivity parameters used in a computational study on the reconstruction of epileptic activity by combined EEG and MEG source analysis [28]. Table 1 presents an overview of the conductivity values (σ = r⁻¹ with r being the resistivity of the compartment) with the mean of each compartment computed with respect to its upper and lower values that were used in this study. The relative deviation is determined between the minimum (maximum) value and the mean value and normalized to it. Figure 2 shows the effect on the current density in the target area for different values of white matter conductivity with the remaining parameters set to their respective mean values (note especially the resulting different orientation components at the target).

Table 1.

Mean, lower and upper boundary, and relative deviation of the conductivity values for the used tissue types.

Tissue type	Conductivity [mS m−1]
	Min	Mean	Max	Rel. Deviation
Skull	1.6	17.3	33.0	90.8%
Skin	280.0	575.0	870.0	51.3%
Gray matter	220.0	445.0	670.0	50.6%
White matter	90.0	190.0	290.0	52.6%

Figure 2.

Current density for auditory cortex stimulation for different values of white matter conductivity 220 mS m⁻¹ (low), 445 mS m⁻¹ (mean), 670 mS m⁻¹ (high). The conductivity of the other compartments is set to their respective mean values.

Baumann et al [29] measured the conductivity of the human CSF compartment at body temperature to be 1.79 S m⁻¹ (averaged over 7 subjects, with a standard deviation of less than 2.4 %). Based on the values in Table 1, the conductivity of skin, skull, gray and white matter was modeled as uniformly distributed random variable. The use of uniform probability distributions accounts for the lack of data on these conductivity values in literature and models a ”worst-case” scenario, in which each conductivity value within the upper and lower boundaries is equally probable. In case of uniformly distributed model parameters, a simple linear transformation can be applied to map the model parameters X onto the random variables ξ and vice versa.

2.5. Global Sensitivity Analysis Using Sobol’ Indices

For the quantification of uncertainty in the model outputs, it is not only of interest how large this uncertainty is, but also which uncertain model parameters contribute in which manner to it. In addition to the sensitivity to each single model parameter, the sensitivity arising from the multivariate influence of the model parameters may result in interaction effects, which are not apparent by only evaluating the isolated uni-variate effects. These global sensitivities can be described by conditional variances 𝕍(i, …, j), which determine the sensitivity of a model output to the model parameters X_i, …, X_j as well as their interactions. The relative conditional variances, which are normalized to the total variance 𝕍 of a model output, are called Sobol’ indices:

$$S(i,\dots ,j)=\frac{𝕍(i,\dots ,j)}{𝕍}.$$ (3)

The Sobol’ indices form a Sobol’ decomposition of the variance of a model output, which is unique in case of an orthogonal basis [19] and can be simply derived from evaluating the coefficients of a multivariate gPC expansion [17]. To investigate if all uncertain model parameters have to be considered in the uncertainty quantification process, the effect of each model parameter is identified in a first screening to examine if its influence is comparatively small. For this purpose, the first order Sobol’ indices derived from the uni-variate gPC expansions for each random model parameter are used.

3. Results

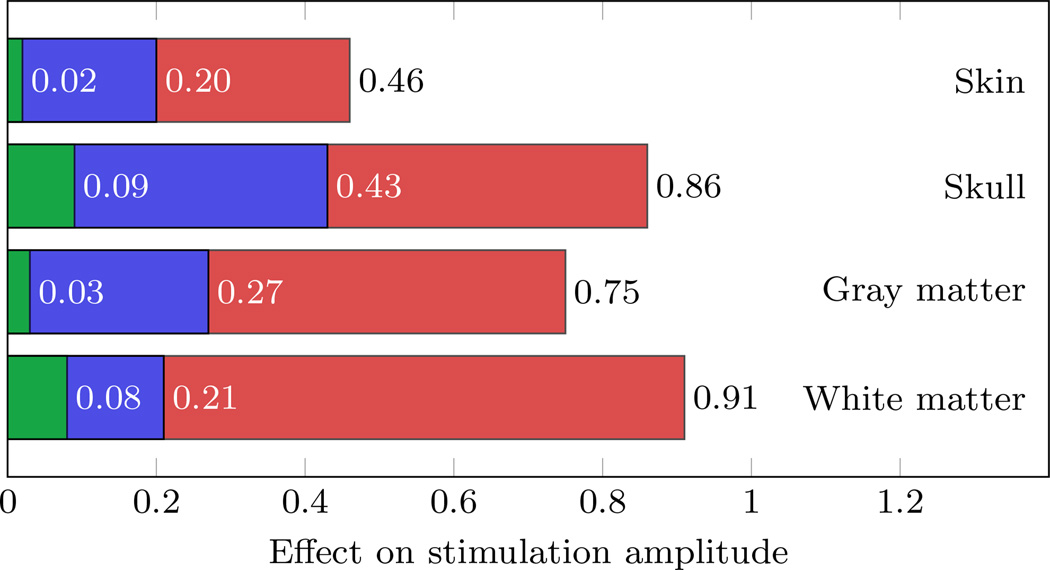
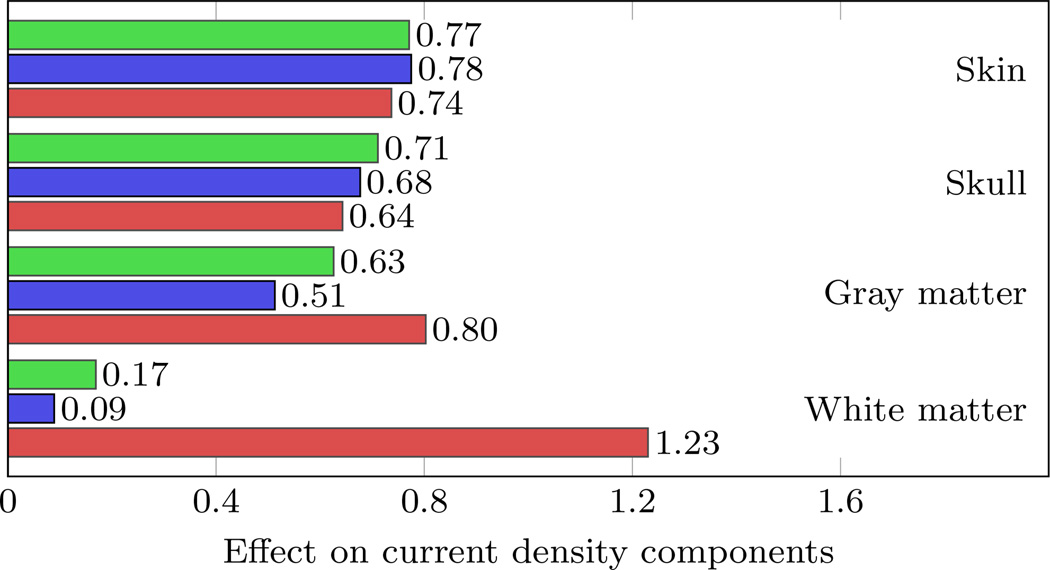
Based on the results of the first screening of the model response determined by the uni-variate gPC expansions and the first order Sobol’ indices, the possibility to reduce the number of crucial random model parameters for the multi-variate gPC expansions were identified. The quantities of interest for the investigation of the appropriate expansion orders of the gPC expansions were chosen to be the stimulation amplitudes at those stimulation electrodes with a mean value greater than 100 µA as well as on the components of the current density at the stimulation target. An expansion order of p = 4 was required to reduce the relative error in the variance of the quantities of interest below 1 %. For those uni-variate gPC expansions, the effect of each tissue conductivity on the amplitudes at the chosen stimulation electrodes was determined (see Figure 3). The effect is defined as normalized relative standard deviation of the quantity of interest with respect to that of the model parameters. The largest effects on the stimulation amplitudes were noticeable for skull, gray matter, and white matter conductivity with a large variation among the chosen stimulation electrodes. Regarding the effect on the current density, the largest effects were on the z-component for gray matter and white matter conductivity, while those for skin and skull conductivity were similar in all components (see Figure 4). Especially for the white matter compartment, the effect on the current density was prevalent on the z-component, while the effect on the x- and y-components was comparatively small. These variations and the magnitudes of each effect on the stimulation amplitudes as well as on the components of the current density necessitated for a consideration of all four model parameters in the computation of the multi-variate case. Based on the convergence results of the uni-variate gPC expansions, the multi-variate gPC expansion was computed up to an expansion order p = 4, which required the evaluation of the deterministic model at a number of 401 parameter samples.

Figure 3.

Minimum (green), Mean (blue), and maximum (red) of the effect of each uncertain conductivity on the stimulation amplitudes for the chosen main stimulation electrodes.

Figure 4.

Effect of each uncertain conductivity on the x- (green), y- (blue), and z-component (red) of the current density.

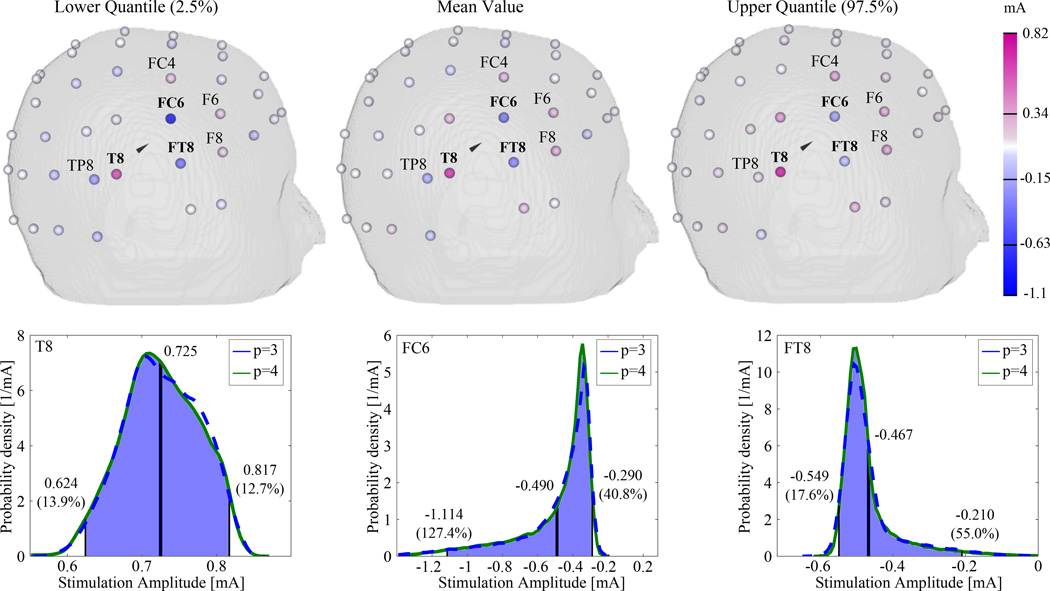
To estimate the probability density functions of the stimulation protocol and the current density at the target, Monte Carlo simulation (MCS) for 1 million random samples was applied on the determined multi-variate gPC expansion. Figure 5 displays the stimulation protocols consisting of the lower 2.5% quantile, the mean value, and the upper 97.5% quantile of the probability density function for each electrode (upper row) and the probability density function of the three main stimulation electrodes T8, FC6 and FT8 for the expansion order p = 3 and p = 4 (lower row). The mean value is depicted by a solid black line and the percentage values show the deviation of the lower and upper quantiles to the mean value. As can be seen in the Figure, the probability density functions are sharp and show a good agreement for expansion orders p = 3 and p = 4, while minor differences can be seen especially at the peaks of the probability density functions. This result suggests that an expansion order of p = 3 was sufficient to approximate the statistics of the investigated quantities of interest. Moreover, the probability density function of electrode T8 was fairly symmetric, whereas an asymmetric behavior can be seen for the FC6 and FT8 electrodes. This asymmetric behavior was mutually opposed for both electrodes, resulting in larger deviations for larger stimulation amplitudes for electrode FC6 and smaller stimulation amplitudes for electrode FT8. With deviations up to 127.4 % and 55 %, the values for the lower and upper quantiles for electrodes FC6 and FT8 showed substantially larger deviations to the mean values as compared to electrode T8.

Figure 5.

Lower quantile, mean, and upper quantile of the uncertain stimulation protocol. For the main anode and the two main cathodes, the estimated probability density functions for 1 million random samples are shown using a gPC expansion of order p = 3 (blue) and p = 4 (green).

As can be seen in Figure 5 (upper row), the stimulation protocols for the auditory target showed great focality and are mainly comprised of three electrodes, an anodal stimulation (i.e. positive stimulation) at electrode location T8 and two cathodal stimulations (i.e. negative stimulation) at electrode locations FC6 and FT8. Moreover, in order to minimize the current density in non-target regions, the optimization algorithm injected weaker compensating currents at neighboring electrodes, especially at electrodes TP8, F8, F6 and FC4.

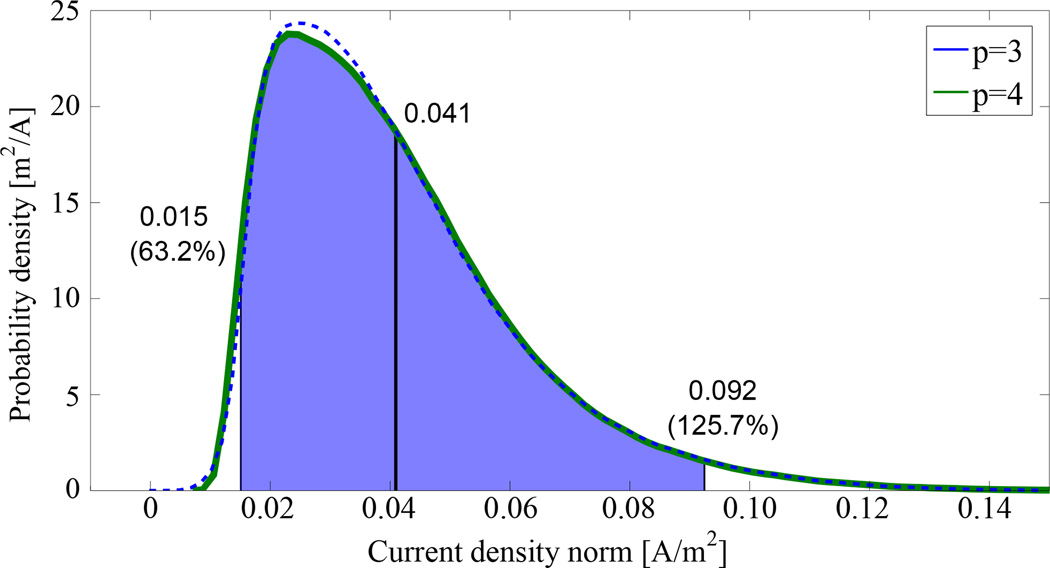
The probability density function of the current density norm showed an asymmetric behavior with a smaller deviation of the lower 2.5% quantile compared to that of the upper 97.5% quantile (see Figure 6). To ensure that the chosen expansion order was sufficient to accurately approximate the behavior of the uncertainty in the current density norm, the probability density function was also computed for a lower expansion order. The evaluation of the lower and upper quantile resulted in an uncertain interval for the current density norm ranging from less than half to more than twice the mean value.

Figure 6.

Estimated probability density function of the current density norm for the expansion orders p = 3 (blue) and p = 4 (green).

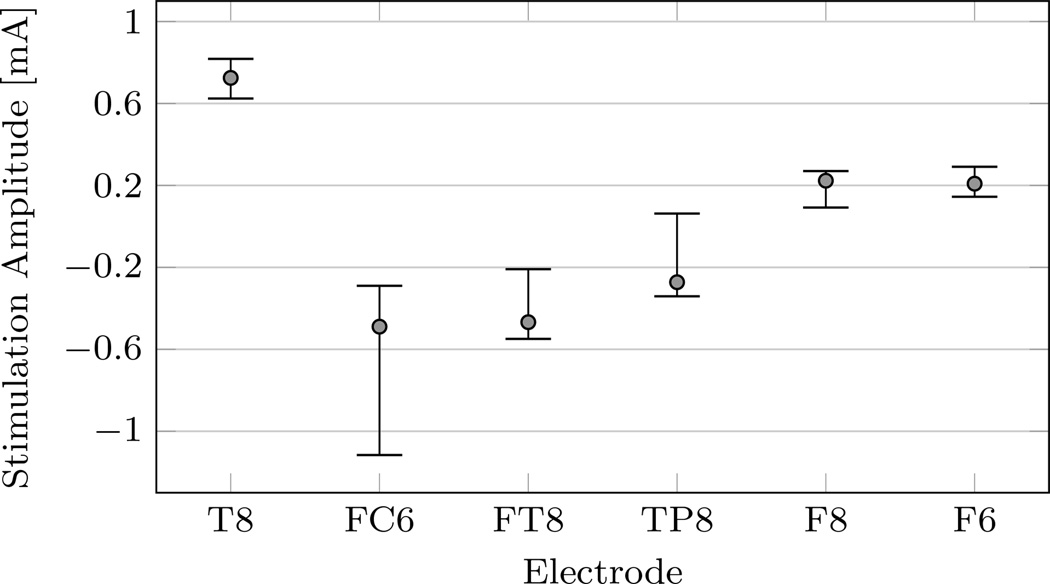
To compare the influence of the uncertainty in the tissue conductivities on the stimulation protocol of the main anode and cathode electrodes, the lower quantile, upper quantile, and mean value of the stimulation amplitudes applied to these electrodes with a mean greater than 200 µA were computed (see Figure 7). While the uncertainty in the stimulation amplitude of the main anode T8 showed an almost symmetric behavior with a deviation of approximately 14% and 13% for the lower and upper quantile, respectively, the stimulation amplitudes at the compensating main cathodes FC6, FT8, and TP8 revealed an asymmetric behavior with comparatively large deviations. With decreasing stimulation amplitudes of the compensating electrodes, these deviations decreased as well, but were still larger than those for the main anode T8.

Figure 7.

Lower quantile, upper quantile and mean of the amplitudes (> 200 µA) of the stimulation electrodes.

The investigation of the Sobol’ indices for the sensitivity analysis of the stimulation amplitudes of the three main electrodes revealed that the stimulation protocol for each electrode is not necessarily influenced by the uncertain brain tissue conductivities in the same extent. In Table 2, the first order Sobol’ indices as well as the higher order Sobol’ indices with values larger than 1% are shown. The first order indices represent the sensitivity of the stimulation amplitude at the specified electrodes with respect to each single uncertain tissue conductivity. Beyond that, the higher order indices allow for an investigation of interaction effects, where only the combination of multiple uncertain parameters results in an uncertain stimulation amplitude. While the stimulation amplitudes at the two main cathodes were most sensitive to uncertainty in the skull conductivity, those at the main anode was influenced at most by the uncertain conductivity of skull as well as white matter in a similar intensity (see Table 2). Furthermore, the stimulation amplitude at the anode showed a sensitivity to the combined uncertainty in the conductivity of skin and skull as well as skull and gray matter. The sum of the first order and listed second order Sobol’ indices for the specified anode and cathodes are larger than 97.5 %, which suggests that the uncertainty in the resulting stimulation protocol can be described almost entirely by those random parameter combinations.

Table 2.

Sensitivity of the stimulation amplitudes of the main electrodes with respect to the uncertainty in each tissue type and their stochastic interactions for the conductivity of skin σ_skin, skull σ_skull, gray matter σ_gm, and white matter σ_wm.

	Sensitivity on Stimulation Amplitude
Parameter	T8 [%]	FC6 [%]	FT8 [%]
σskin	5.9	7.7	4.0
σskull	28.9	79.8	70.1
σgm	16.2	6.9	13.0
σwm	27.2	0.5	3.1
σskin, σskull	12.0	3.5	6.6
σskull, σgm	7.3	1.2	2.8
∑	97.5	99.5	99.6

4. Discussion

The objective of this study was to investigate the influence of inter-individually varying conductivity profiles on optimal electrode configurations for an auditory cortex stimulation using a multi-array transcranial direct current stimulation (tDCS). A realistic five-compartment finite element head model was generated and the alternating direction method was used for numerical realization of the considered optimization problem (1). In order to quantify the uncertainty of the optimal electrode configurations, a multi-variate generalized Polynomial Chaos (gPC) expansion was used and the stochastic measures, probability density functions and sensitivity of the quantities of interest were investigated. Moreover, the lower 2.5 % quantile, the mean value, and the upper 97.5 % quantile of the probability density function of the optimal electrode configurations and the resulting stimulation current throughout the head domain were computed and visualized using the software package SCIRun⁺.

To obtain a sufficient accuracy in the investigated quantities of interest, uni-variate gPC expansions for each uncertain model parameter were computed to control the approximation error in each dimension. The number of required model realizations for the uni-variate expansions as well as those for the multi-variate expansion resulted in a total number of 465 deterministic samples. For the estimation of the probability density functions of the quantity of interests, Monte Carlo Simulation (MCS) with 1 million random samples applied to the computed gPC expansions was used. A computation of the uncertainty in these quantities using, for example, the classic MCS directly on the computationally expensive deterministic model would have required a comparatively large number of random model realizations to provide a sufficient accuracy [15]. Considering the computation time for one model realization of approximately 80 min (approx. 60 min for the 73 forward problems to compute the matrix A in equation (1) and 20 min for the inverse optimization), the use of MCS for the uncertainty quantification would have taken an excessive amount of computer resources and time. Therefore, the applied gPC method allowed for a computation of the uncertainty in the stimulation protocol and the current density at the target in a reasonable time by distributing the computational load on common workstations.

For the auditory target vector, a large variability of the effect of each tissue conductivity on the stimulation amplitudes of the electrodes can be noted (see Figure 3), which is in agreement with the stochastic measures of the multi-variate gPC expansions of the stimulation protocol visualized in Figure 7. Both Figures show a trend of larger deviations of likely higher stimulation amplitudes compared to their respective mean values. Since all mean effects were between 0.20 and 0.43 with maxima between 0.46 and 0.91, the investigation of the effect based on the uni-variate gPC expansions did not allow for the exclusion of one random parameter by treating it as deterministic. A similar effect characteristic was noticeable for the investigation of the current density (see Figure 4). However, the effect regarding white matter conductivity showed a different behavior, with a dominant effect in its z-component. A possible explanation for this behavior is given in the following paragraph.

As can be seen in Figure 1, the auditory target vector was located on a gray matter gyrus. The distance to the nearest white matter region into the z-direction was below 2 mm. The z-coordinate of the target vector was thus oriented along the vertical axis and oriented from the white matter compartment to the gray matter compartment. When decreasing the white matter conductivity while keeping the conductivity values of the other compartments constant, stronger current densities were noticeable in the gray matter compartment, in line with Wagner et al [2]. This implies that in case of a low white matter conductivity, weaker currents were flowing from the gray matter into the white matter, resulting in very weak current densities in this compartment. Because the z-component of the auditory target vector was pointing from white matter to gray matter and most of the target current density was conducted through the gyrus when considering a low white matter conductivity, the orientation of the current density at the target changed substantially, leading to a very weak z-component. Therefore, the higher the white matter conductivity, the less current density was noticeable in the gyrus, resulting in an increased z-component of the target current density. Because the distance of the target vector to the nearest white matter element into the x- and y-direction was larger than 10 mm, the x- and y-components of the target vector remained nearly identical when decreasing the white matter conductivity. This demonstrates that for the white matter compartment the effect on the current density was dominated by the z-component, while the effect on the x- and y-components was comparatively small (see Figure 2).

The current density distribution and focality in the head model also depends on the modeling of the stimulation electrodes. In this study, we used point electrode models (PEM), which assume the stimulation electrodes to be neutral elements on the head surface. This approach does not account for the non-uniform current density profile in the proximity of the stimulation electrodes [6, 7, 8]. Recently performed computer simulations confirm the difference between both electrode models at the interface between the stimulation electrodes and the head model, but have shown only subtle deviations of the current density within the brain region [9]. Referring to these results and similar results reported in a computational study on EEG simulation [10], it is expected that due to the comparatively higher current density maxima for PEM, the application of CEM might allow for a larger total stimulation current. However, it is not expected that the CEM will significantly change the overall results of this study.

Comparing the deviations in the uncertain model parameters in Table 1 with those of the current density norm in Figure 6, the results suggest that uncertainty in tissue conductivity should be considered when predicting optimal stimulation protocols in computational models of tDCS, especially when assuming the magnitudes of uncertainty as considered in this study. A similar statement can be objected for the corresponding uncertain stimulation protocol with comparative deviations in the stimulation amplitudes of the compensating main cathodes. However, it should be noted that the deviations in the stimulation amplitude of the main anode, which excites the target at most, were comparatively small and can be considered to be tolerable with regard to the prescribed level of uncertainty in tissue conductivity. In this context, depending on the orientation (either radially inwards or outwards) of the target cortical area underneath the stimulating electrode, an anodic stimulation might lead to both excitation or inhibition, as shown by [30, 31].

An important question raised in many tDCS experiments is whether a weak direct current stimulation can have therapeutic effects or not. Francis et al [32] were able to demonstrate that an electric field of about 140 µV mm⁻¹ is able to enhance the firing rate of neurons. Considering the mean gray matter conductivity value of 0.44 S m⁻¹ in this study, the current density amplitude should thus be greater than 0.062 A m⁻² in order to have therapeutic effects. As the mean value of the probability density function of the current density norm was approximately 0.041 A m⁻² (Figure 6), the probability that the current density amplitude in the target region is supra-threshold [32] is below 50 %. This might be due to the fact that the auditory target vector was located on a deeper part of the gyrus and relatively large upper and lower bounds of approximately ± 50% of the conductivity values were considered. In order to obtain greater probability for an effective and well-targeted stimulation, the total current applied to the electrodes might be enlarged. Because the current density amplitude is linear, a total current of approximately 3.1 mA would ensure that, with a probability of greater than 50 %, the current density norm at the target is greater than 0.062 A m⁻². Clinical studies might be performed in order to investigate the influence of larger input currents with regard to patient safety and the effects of stimulation.

The stimulation protocol for each electrode is influenced to a different extent by the conductivity variations of each considered tissue compartment (see Table 2). In addition, the sensitivity of the stimulation amplitudes for each electrode will most likely depend on the location of the chosen stimulation target as well. Therefore, it was not possible to reduce the number of considered uncertain parameters for the investigation of the entire stimulation protocol. The major influence on the stimulation amplitudes of the main anode and cathodes is pooled in the first order Sobol’ indices, representing the solely influence of each uncertain parameter. Stochastic interaction effects of the conductivity of the neighboring compartments skin and skull as well as skull and gray matter were especially noticeably for the stimulation amplitude of the main anode T8, but also with a smaller extent for the main cathodes FC6 and FT8. The results suggest that almost the entire uncertainty of the stimulation protocol of the main electrodes can be described by the first order and the mentioned second order interaction effects of the uncertain conductivities, which further suggests that higher order interaction effects of these model parameters are negligible in the stochastic model. This information can be useful for future studies to reduce the parameter space dimension by considering less uncertain model parameters and to divide the parameter space in distinct parameter subspaces, which would further reduce the computational expense and, therefore, the computation time for the evaluation of the uncertain stimulation protocol. Furthermore, the determined interaction effects of the uncertain conductivities on the stimulation protocol in this study, especially for the main anode, propose that a multi-variate modeling and quantification of the uncertainty in the stimulation protocol is inevitable. This result and the level of uncertainty determined in the stimulation protocol based on the levels of uncertainty for the tissue conductivities assumed in this study, require for an inclusion of parametric uncertainties in the optimization of the stimulation protocol and the use of multi-variate stochastic methods, which will require more sophisticated approaches regarding robust optimization techniques. However, it should be noted that the levels of uncertainty assumed in this study in the conductivity of the considered parameters reflect a ”worst-case” scenario with the maximum range of literature values used to model the uncertain conductivities of the respective compartments. In practice and with patient-individual information on the electrical properties of the different tissue types, the resulting uncertainty in the predicted stimulation protocol may be smaller. Despite the known challenges in the measurement of the electrical properties of biological tissue and the variations in literature data [11, 12, 13, 28], quantification of the uncertainty in the predictions derived from computational models concerning bio-electrical applications is still scarce. Nowadays, the detailed and systematic investigation of uncertainty in computational models becomes of larger interest for various bio-electrical applications. In previous studies, uncertainty in the prediction of the therapeutic effect in deep brain stimulation in dependence of the electrical properties of brain tissue and the parameters of the electrode-tissue-interface was investigated in a volume conductor model of the human brain [16, 25]. Geneser et al [33] investigated the impact of uncertain rate coefficients in Markovian ion channel models on the macroscopic electrical current through these channels. Regarding the computational modeling of the electroencephalography (EEG) forward problem, which is closely related to the modeling approach for the optimization of the stimulation protocol in tDCS presented in this study, a recent study investigated the influence of uncertain conductivity and the sensitivity on the sensorial response of the EEG electrodes with respect to uncertainty in the conductivity of brain tissue as well as in the location and the moment of the source dipole [34]. In addition, a correlation analysis was performed, suggesting that for sources in the cerebrum and cerebellum, sensors located temporally were highly correlated, whereas sensors in occipital and lower frontal region were comparatively less correlated, despite their close locations. The study models the uncertainty in brain tissue conductivity in a simplified manner as the fraction of skull and brain tissue conductivity in a three-layered spherical head model. This approach introduces a stochastic dependence of both tissue conductivities, which might differ from real dependencies. Since literature data on these information is scarce, we assumed the considered uncertain biological tissue conductivities to be mutually independent. In addition, a realistic head model is used in this study representing the anatomy of the human brain, allowing for a detailed evaluation of the effects of the uncertain conductivity of each compartment on the optimized stimulation protocol as well as the current density at the target. To the authors’ knowledge, this study presents the first detailed and profound investigation of the uncertainty and sensitivity in an optimized stimulation protocol for tDCS with respect to the variations in the conductivity of the compartments of the human head.

Uncertainty in the parameters of computational models describing bio-electrical applications do not only arise from the varying electrical properties of biological tissue, but may also be based on uncertain geometry parameters as well as varying locations and orientations of the targets and sources of interest. Regarding uncertain locations and orientations of sources in the electrocardiographic (ECG) forward problem, Swenson et al [35] used the gPC method in combination with a sampling based on sparse Smolyak grids to predict changes in heart location and orientation on body-surface ECG potentials. The advantage of such a non-intrusive formulation of the gPC method is that the underlying deterministic model describing the bio-electrical application can remain unchanged. However, there are also computational studies investigating models of bio-electrical applications, where an intrusive formulation of the gPC method, which requires a modification of the model equations, is feasible, as for example a study on the effect of uncertain conductivity on ECG potentials of the human thorax [36].

The guideline for efficient yet accurate volume conductor modeling in tDCS [2] was used to identify the most important tissue compartments to be investigated. In this study, we only focused on the five most important isotropic tissue compartments skin, skull, cerebrospinal fluid (CSF), gray matter and white matter for tDCS [2], while for the sake of substantial reduction of computational complexity, skull compacta and spongiosa modeling and white matter anisotropy modeling were excluded. The approach to model the skull as one compartment without dividing it into compacta and spongiosa is in agreement with results from a computational study, which investigated the influence of the detailed modeling of the skull compartment [28]. Detailed investigations of the combined effects of anisotropy and uncertainty in white matter conductivity in the presented model will be carried out in future studies by using common modeling approaches based on the linear relationship between the diffusion of water molecules and electric conductivity in the neuron fibers [37, 38].

Because the conductivity value of the human CSF at body temperature is well-known [29], the corresponding compartment was modeled as a deterministic model parameter. Nevertheless, a proper modeling of the CSF compartment is important to obtain realistic current density distributions, as clearly shown in [2]. The importance of modeling CSF has recently also been shown experimentally using MRI and visual paradigms in EEG, where the brain shift and the resulting small changes in the thickness of the CSF layer, induced by changing the subject’s position from prone to supine, were shown to have a significant effect on the EEG [39].

The results and conclusions of this study are based on the investigation of one target vector for one-hemispheric auditory cortex stimulation. While the determined auditory target in this study had a deeper location and was therefore difficult to stimulate (see Figure 2, where the maximum stimulation is more superficial and not at the deeper target side), the stimulation of more lateral targets will be more successful (see also [4]). For superficial targets, where no white matter is located between the target and the stimulation electrodes, the white matter conductivity is expected to be far less important [2]. In such cases, this compartment might be excluded from the multi-variate gPC expansion, reducing drastically the number of required model realizations and, therefore, the computational amount of work for the sensitivity investigation and increasing the stability of the simulation results [40]. In a future study, we thus plan to quantify the uncertainty of the optimal electrode configurations for a superficial target vector and investigate the differences in the stochastic measures, probability density functions and sensitivity of the quantities of interest.

Even more importantly, the first order Sobol’ indices depicted that the probability density function of the stimulation protocols at the two main cathodes and at the main anode were most sensitive to uncertainty in the skull conductivity (see Table 2). In order to reduce the large deviations in the stimulation protocol of the compensating cathodes, a skull conductivity calibration method using simultaneously acquired somatosensory evoked potential and field measurements might be used [14, 28, 41, 42] to individually estimate the skull conductivity parameter of a subject. In this case, the calibrated skull conductivity value can be used as a deterministic model parameter, which further strongly reduces the number of required parameter samples for the computation of the multi-variate gPC expansions and might also reduce the uncertainty of the stimulation protocols at the main anode and cathodes.

5. Conclusion

In this study, the influence of inter-individually varying conductivity profiles on optimal electrode configurations as well as the sensitivity of the conductivity parameters to the target intensity for a target source in auditory cortex and thus deeper location was investigated. In order to quantify the uncertainty of the optimal electrode configurations, a multi-variate gPC expansion was used and the stochastic measures, probability density functions and sensitivity of the quantities of interest were investigated. Using this expansion, we demonstrated that, for a standard 10/10 EEG system with 74 electrodes, the optimized stimulation protocols were mainly comprised of three electrodes, an anode at electrode location T8 and two cathodes at electrode locations FC6 and FT8. With deviations below 15 %, the lower and upper quantiles for the anode at location T8 showed only minor changes to the mean values, while substantially higher deviations up to 127.4% and 55% can be seen for the cathodes at locations FC6 and FT8. The investigation of the sensitivity of the conductivity parameters to the target intensity revealed that the largest effects were on the z-components of the target current density for gray matter and white matter, while those for skin and skull were similar in all components. Regarding the effect on the optimized stimulation protocol, the stimulation amplitudes were most sensitive to skull conductivity. Finally, with a probability greater than 50 %, the optimized stimulation protocol for the deeper auditory target induced sub-threshold current density amplitudes at the target region.