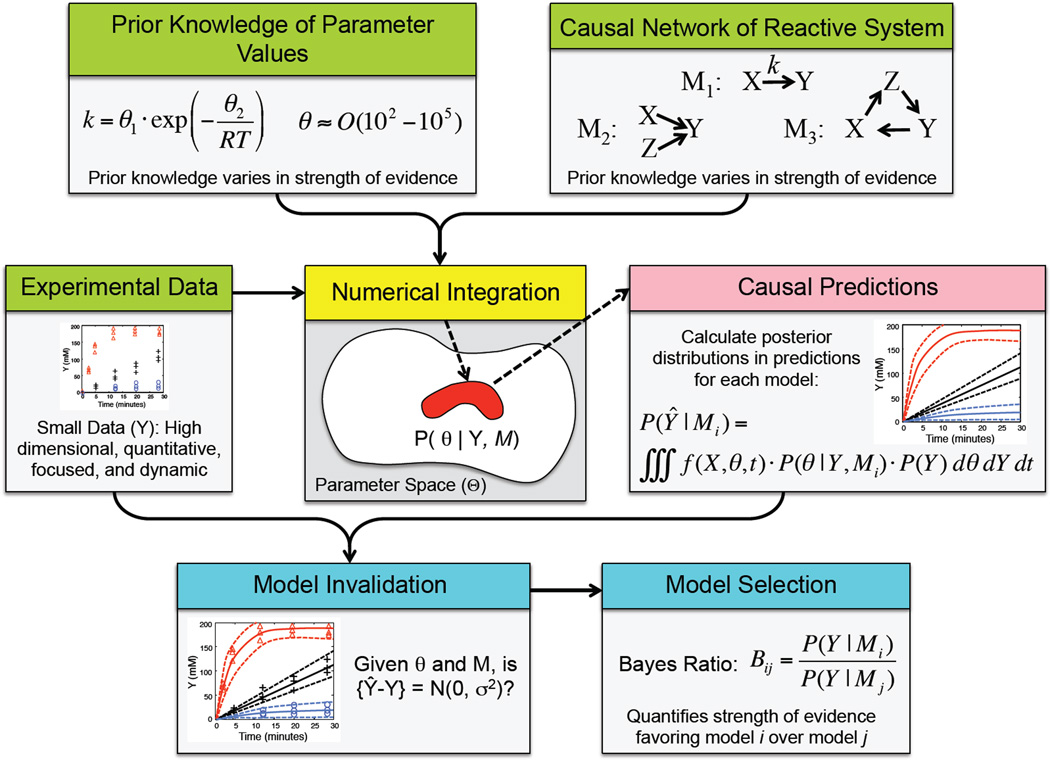
Figure 5. A schematic of an emerging approach for inverse problems that use mechanistic mathematical models of reactive systems.

This approach leverages concepts from Bayesian statistics, probability, and advances in computational power to test competing hypotheses regarding causal structure of the reaction network. A mechanistic model of the reactive system, prior knowledge of parameter values, and experimental data are inputs to a computational filter. If prior knowledge of the key processes that govern the behavior of the reactive systems is weak, multiple competing hypotheses could be pro-posed as a reaction network. If prior knowledge of the parameter values is also weak, the computational filter uses this information as it searches parameter space to select a statistically-based ensemble of parameter values (red region of parameter space), given the uncertainty in the experimental data and model. This ensemble of parameter values are then used to generate a corresponding ensemble of predictions that describe probabilistically how the system evolves in time from the initial values, given the specific data and network model. A model invalidation step involves testing whether the difference between the model pre-dictions (Ŷ) and experimental data (Y) do not have systematic differences (i.e., {Ŷ − Y} ≠ N(0, σ²)). Finally, a Bayes Ratio can be used to select among competing hypothesis as to the governing processes associated with the reactive system.