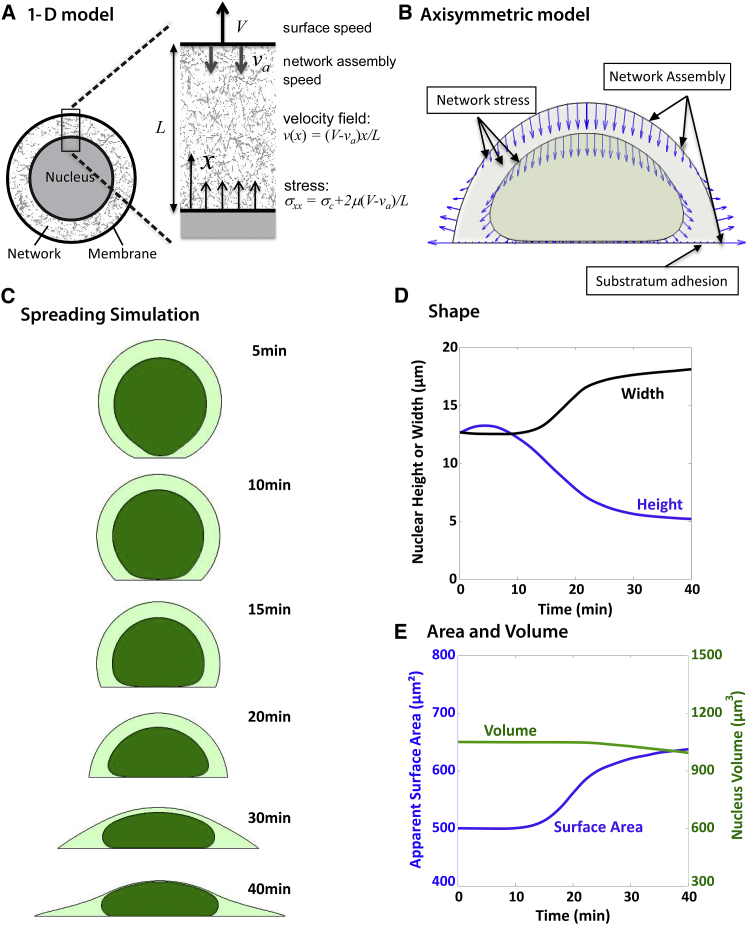
Figure 9.

Mathematical model for nuclear deformation during cell spreading. (A) Predictions of a simplified one-dimensional model for the cytoskeletal network spanning the gap between the nuclear surface and the cell membrane. Movement of the membrane relative to the nuclear surface (speed $V$) or assembly of network at the surface and resulting retrograde flow (speed $v_a$) results in expansion or compression of the intervening network, thereby generating a stress on the nucleus surface. (B) Key components of the model for a spreading cell. The model cell accounts for 1) resistance of the nucleus to volume expansion/compression; 2) resistance of the nuclear surface (lamina) to area expansion; 3) cell membrane tension; and 4) the cytoskeletal network phase of the cytoplasm, which is assembled at the cell cortex and at the contact boundary with the substratum. Centripetal flow of network and the frictional resistance to shear and to volume expansion/compression causes movement of the cell membrane and nuclear surfaces (surface velocities of cell and nuclear surfaces are shown by blue vectors). (C) Snapshots from a simulation of cell spreading and nuclear shape changes showing the three phases of nuclear deformation observed experimentally: 1) vertical distension and translation of the nucleus toward the substratum, driven by flow of network from the apical membrane where it is generated; 2) initial flattening against the substratum with a decrease in nuclear height and little change in nuclear width as the cell begins to spread and the nuclear is compressed vertically by the lowering upper cell surface; and 3) widening of the nucleus with lesser change in height, as the widening cell boundary pulls the nucleus laterally. Widths and height are plotted in (D). As in the experimental observation, the nucleus quickly flattens vertically early in the process of cell spreading, then widens more slowly as the cell continues to spread. (E) Plot of nuclear area and volume versus time. While the nuclear volume remains nearly constant, the area expands until the assumed excess area is smoothed and the stiffer true surface area is reached, at which point the surface area starts to level off toward a constant value. To see this figure in color, go online.