Automated quantitative 3D analysis of aorta size, morphology, and mural calcification distributions

Abstract

Purpose:

The purpose of this work is to develop a fully automated pipeline to compute aorta morphology and calcification measures in large cohorts of CT scans that can be used to investigate the potential of these measures as imaging biomarkers of cardiovascular disease.

Methods:

The first step of the automated pipeline is aorta segmentation. The algorithm the authors propose first detects an initial aorta boundary by exploiting cross-sectional circularity of aorta in axial slices and aortic arch in reformatted oblique slices. This boundary is then refined by a 3D level-set segmentation that evolves the boundary to the location of nearby edges. The authors then detect the aortic calcifications with thresholding and filter out the false positive regions due to nearby high intensity structures based on their anatomical location. The authors extract the centerline and oblique cross sections of the segmented aortas and compute the aorta morphology and calcification measures of the first 2500 subjects from COPDGene study. These measures include volume and number of calcified plaques and measures of vessel morphology such as average cross-sectional area, tortuosity, and arch width.

Results:

The authors computed the agreement between the algorithm and expert segmentations on 45 CT scans and obtained a closest point mean error of 0.62 ± 0.09 mm and a Dice coefficient of 0.92 ± 0.01. The calcification detection algorithm resulted in an improved true positive detection rate of 0.96 compared to previous work. The measurements of aorta size agreed with the measurements reported in previous work. The initial results showed associations of aorta morphology with calcification and with aging. These results may indicate aorta stiffening and unwrapping with calcification and aging.

Conclusions:

The authors have developed an objective tool to assess aorta morphology and aortic calcium plaques on CT scans that may be used to provide information about the presence of cardiovascular disease and its clinical impact in smokers.

1. INTRODUCTION

Manifestations of cardiovascular disease include mural calcification of atherosclerotic plaques, arterial stiffening, and aneurysmal dilation of the aorta.^1,2 In particular, calcification of the thoracic aorta is an important biomarker that is commonly measured in clinical investigation in CT scans and has been linked with coronary calcium,³ cardiac risk factors,⁴ and outcomes such as stroke and myocardial infarction.³ The relationship between atherosclerosis and vascular geometry and regional blood flow and wall shear stress⁵ has been well documented.⁶ Recent studies reported the changes in vessel morphology, and stiffening of vessel with aging and its implications.^7–10 A more extensive evaluation of associations between vessel morphology and mural calcifications can provide clinically important data. We therefore sought to develop a fully automated tool that could be applied to a large number of volumetric chest CT scans being obtained for therapeutic, epidemiologic, and genetic investigations of smoking related diseases.

The first step of the proposed automated pipeline is aorta segmentation, which, in the noncontrast CT scans, is complicated by the similar CT attenuation values of adjacent structures in the mediastinum. Therefore, a standard 3D segmentation technique based solely on edge or intensity information fails without either a good initialization or integration of a 3D shape model to limit leakage into neighboring vessels with similar Hounsfield intensity values. Most previous work^11–14 addressed these difficulties with an approach that relies on a priori shape models built from manually segmented training aorta centerlines. However, small training sets cannot represent the anatomical variabilities of aorta shapes and modeling anatomical variabilities across subjects requires a complex 3D shape model. Constructing this model requires a large set of manually labeled training examples, which is expensive to obtain. To omit the need for a complex a priori shape model, we propose a two stage approach that uses a simpler 2.5D model to construct a good initial surface in the first step and refines this surface in 3D in the second stage with a 3D gradient-based level-set segmentation algorithm. Since standard 3D level-set segmentation algorithm is sensitive to initialization, the first step provides a good initial surface to this algorithm. We use the information that aorta has a tubular candy cane shape with circular cross sections and construct the initial surface by optimizing for the circle parameters using both within slice and between slice information. One shortcoming of the circular cross section assumption adapted from previous work is that it is only an approximation to the true aorta cross section and aorta cross section might deviate from a circle in some axial slices. The level-set algorithm in the second stage solves this problem and refines the initial surface by evolving it to the nearby edge locations.¹⁵ Level-set algorithm operates fully in 3D and results in a smooth segmentation of aorta. We first reported this segmentation algorithm in IEEE EMBC 2012 conference paper.¹⁶ Herein, we more extensively explain the improved version of the segmentation algorithm, explain methods to extract morphology and calcification measures, and evaluate the performance of these measures on a large cohort of 2500 smokers.

The second step of the pipeline is detection of mural calcifications using an attenuation threshold applied to the segmented aortas. Previous efforts to quantify aortic calcification utilized an atlas based approach for vascular segmentation¹⁷ followed by aortic calcification detection. However, due to variable anatomy of the mediastinum, such an approach may lead to inaccuracy in segmentation and detection of many false positive calcified plaques that are due to nearby high density regions such as vertebra and calcifications in trachea wall. Instead, we used our more refined aorta segmentation for calcification detection followed by a filtering approach based on anatomy to eliminate many of the false positives.

The final step of the automated processing pipeline after aorta segmentation is the extraction of vessel morphology features. The complete pipeline is summarized in Fig. 1.

FIG. 1.

Flow chart of the fully automated pipeline.

The main contributions of the proposed work to the literature are the following.

• •A fully automated pipeline for aorta segmentation and calcification detection is introduced. Unlike previous work⁸ that operated on manually placed seed points to initiate segmentation and define its cranial and caudal limits, our work is fully automated and selects the seed points automatically based on detected landmarks.
• •A two step segmentation approach is proposed. The first step constructs an initial surface using an approximate circular shape model of aorta cross sections and an additional component in the third dimension to impose smooth parameter transitions from slice-to-slice. The second step is a 3D level-set segmentation algorithm that uses the boundary surface from the first step as a good initialization that helps to converge to a better local optimum. The second step locally refines the initial surface while keeping the surface smooth in 3D.
• •A set of measures representing the vessel morphology and calcifications are defined and computed. Unlike most of the previous work that computes vessel radius or cross-sectional area in 2D axial planes, our pipeline computes these features more accurately in 3D after automated extraction of centerline and cross-sectional planes that are normal to centerline.
• •Objective quantitative assessment of vessel morphology and mural calcification is performed using a large cohort of 2500 smokers from the multicenter COPDGene study. The range of the computed measures is compared with the numbers reported in the recent literature as another way of validating the algorithm’s performance when applied on a large cohort. The associations of these quantitative image biomarkers with each other and with age are investigated.

The paper is organized as follows. In Secs. 2.A and 2.B, we describe the automatically extracted landmarks and introduce the automated aorta segmentation algorithm. In Sec. 2.C, we explain detection and objective quantification of global and regional measures of mural calcification. In Sec. 2.D, we describe how we extract aorta centerline and the oblique cross-sectional planes. We then explain how we compute the aorta size and morphology measures in Sec. 2.F. In Secs. 3.A and 3.B, we describe the data and explain how we validate the segmentation and calcification detection algorithms. In Sec. 3.D, we explain validations on large cohort and report the associations between the extracted imaging measures and clinical and epidemiological measures of COPD. We finally summarize our findings and the impact of the work in Sec. 4.

2. METHODS

2.A. Localization of anatomical landmarks

As the first step, some anatomical landmarks are located to initialize the aorta segmentation and to crop the original volume to reduce the computational cost. These landmarks are the main carina [bifurcation point of trachea into left and right main bronchi, indicated with a red circle in Fig. 2(a)] and the bounding box of lungs. We locate lung and trachea using a standard 3D region growing algorithm.¹⁸ The lung bounding box is then calculated from the segmented lungs and used to crop the original volume in anterior–posterior and medio-lateral directions. In medio-lateral direction, the volume is cropped around the detected trachea carina location with a window width of half the lung bounding box size. The anterior, posterior, and superior sides of the volume are cropped at the positions of the full lung bounding box [Fig. 2(a)]. A smaller VOI is obtained after cropping.

FIG. 2.

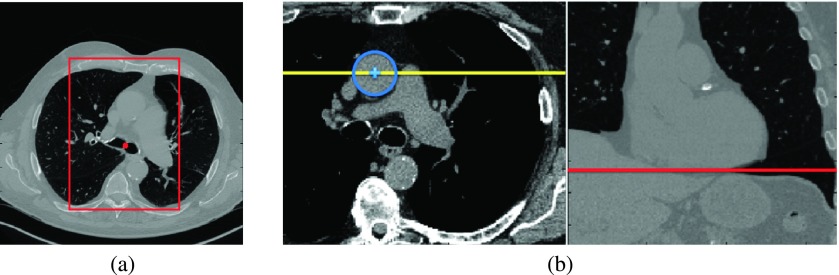
(a) Red rectangle shows the VOI boundaries in anterior–posterior and left–right directions. (b) Left panel shows the axial slice of trachea bifurcation, the center of ascending aorta (blue plus), and the coronal slice location (yellow line). Right panel shows the coronal slice and the detected inferior boundary for the VOI (red line).

2.B. Aorta segmentation

We apply a 3D level-set segmentation technique for aorta segmentation that evolves an initial surface locally to the nearby edge locations while keeping the surface smooth. We first explain how we construct a good initial surface combining ideas adopted from the literature. We then explain how an edge based 3D level-set evolution is applied to locally refine this initial surface to the nearby edge locations corresponding to the aorta boundaries.

2.B.1. Initial Aorta Boundary Surface Construction

We first obtain an initial aorta boundary surface using the approximate anatomical definition of the aorta shape, which is composed of a tubular candy cane shape where the arch section has a half torus shape and descending (DA) and ascending (AA) aorta sections have tubular shapes. The DA and AA cross sections also tend to be circular in axial slices and aortic arch sections tend to be circular in the oblique slices along the half torus arch shape. We search for circles in axial slices to find DA and AA and in reformatted oblique slices to find the arch. We apply this circle detection sequentially starting from the slice of main carina of the trachea using a similar approach described in Ref. 14. This is where we locate the initial circles corresponding to DA and AA as explained in Appendix A.

The sequential circle detection is composed of two steps.

• 1.We first apply a circular Hough transform (HT) to the current slice to detect the circles within Δr radius and Δd distance to the circle detected in the previous slice.
• 2.Our goal is to find the circle C_i that maximizes the posterior probability associated with the maps given the observed image slice S, the HT map, and the spatial smoothness prior. We represent a circle by three parameters: x and y coordinates of its center and its radius.
  The circle C_i maximizing the posterior probability given the image slice S and the circular HT is calculated as

  $${\displaystyle \widehat{C_i}=arg\underset{\underset{i}{C}}{max}\hspace{0.17em}p\left(C_i\right|S,\mathrm{HT})\propto P\left(S\right|C_i)P\left(\mathrm{HT}\right|C_i)P\left(C_i\right)}$$ (1)

  $${\displaystyle P\left(S\right|C_i)P\left(\mathrm{HT}\right|C_i)P\left(C_i\right)=\prod _{x\in \mathrm{Interior}\left(\underset{i}{C}\right)}P\left(S_x\right|C_i)P\left(\mathrm{HT}\right|C_i)P(C_{i-1},C_i).}$$ (2)

  By taking the logarithm of the posterior probability, the estimate of C_i can be formulated as

  $${\displaystyle \widehat{C_i}=arg\underset{\underset{i}{C}}{max}\hspace{0.17em}R\left(C_i\right)=\sum _{x\in \mathrm{Interior}\left(\underset{i}{C}\right)}{R}_{\mathrm{int}}\left(x_i\right)+R_{\mathrm{HT}}\left(C_i\right)+R_{\mathrm{sm}}(C_{i-1},C_i),}$$ (3)

  where R_int, the intensity term, is the logarithm of the aorta intensity probability (modeled by a Gaussian distribution with mean m_I and standard deviation σ_I) of a voxel within a candidate circle. R_HT = log P(HT|C_i) is the Hough transform value term and is equal to the value of a circle in the Hough map indicating the strength of that circle. R_sm(C_i−1, C_i) = log P(C_i−1, C_i), the smoothness term, is the one norm of the distance between parameters of the circle in current slice and previous slice.

  The circle maximizing this energy function R(C_i) is selected.

We apply this sequential circle detection method to axial slices along the tubular DA and AA sections starting from the slice of carina and moving caudally. AA circle detection stops when no AA circle is detected in five consecutive slices due to AA cross section shape deviating from a circle when it starts bending toward the heart. We choose that point as the inferior end point of AA. DA is detected using the similar sequential detection approach until the inferior end point of cropped volume.

We detect circles along aortic arch within reformatted oblique cross sectional planes along the half torus shape of aortic arch. The method for constructing reformatted oblique slices along the half torus arch shape adapted from Kovacs et al.¹² is explained in Appendix B (see Fig. 3).

FIG. 3.

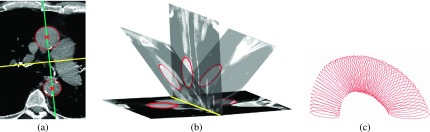
(a) In the slice of main carina, detected DA and AA circles and their centers are shown in red (circles and crosses), the (vertical) line through these centers is shown in blue and the second (horizontal) line normal to the first one is shown in yellow. (b) The vertical plane taken from the location of yellow line is shown together with some example oblique planes obtained by rotating that vertical plane. The circles detected sequentially in these oblique planes are indicated by red. (c) Circles detected in all consecutive oblique planes are shown.

We detect circles in finely sampled consecutive slices (every other slice) simply because when a circle is not detected in one slice due to noise or cross section deviating from a circular shape, we skip that slice and detect the circle in the next slice. The missing circles are recovered during the following step.

2.B.1.a. 3D surface construction.

After detecting circles, we first apply 3D least squares spline curve fitting to the center and radius values of the detected circles along the aorta to fill in the missing circle locations. We then sample points along the circles and generate a 3D triangulated mesh from this point cloud. Finally, we convert this triangulated mesh to a boundary surface by splitting the triangulated faces until the size of each edge is smaller than half of a voxel. The voxel beneath that small triangle is set to be a boundary voxel.

2.B.2. Segmentation refinement using 3D level-sets

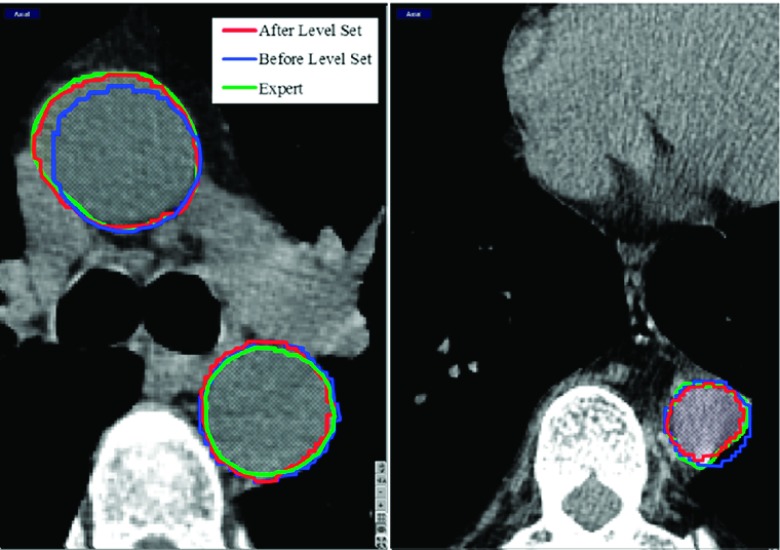
We finally refine the location of this initial aorta boundary surface with a 3D level-set segmentation algorithm. This algorithm evolves the initial boundary to the nearby edge locations while simultaneously maintaining the smoothness of its shape. The refinement is especially effective when the aorta cross sections deviate from being circular in some axial or oblique slices, some of which are often located in slices close to the arch region. See Fig. 4 for some examples.

FIG. 4.

The initial aorta boundaries (blue: Before Level Set) and the boundaries after level-set refinement (red: After Level Set), and the expert boundary (green: Expert) are shown. For slices where the cross section is not perfectly circular, the refinement step moves the boundaries to the nearby edge locations.

For level-set segmentation, the aorta boundary is represented implicitly as the zero level surface of some embedding level-set function (Φ). This embedding function is calculated as the signed distance of each voxel in the image domain (Ω) to the boundary surface. We compute this function using the fast marching algorithm.¹⁹ The initial function is evolved to minimize an energy function. We use a level-set energy function (E(Φ)) including standard energy terms which are edge matching E_edge, level set regularization (E_reg,²⁰) and smoothness (E_sm) terms,²¹

$${\displaystyle E\left(\mathrm{\Phi }\right)=E_{\mathrm{edge}}\left(\mathrm{\Phi }\right)+\lambda E_{\mathrm{reg}}\left(\mathrm{\Phi }\right)+\nu E_{\mathrm{sm}}\left(\mathrm{\Phi }\right)={\int }_{\mathrm{\Omega }}g\left(I\right){\delta }_{ϵ}\left(\mathrm{\Phi }\right)\left|\nabla \mathrm{\Phi }\right|\mathrm{d}\mathrm{\Omega }+\lambda {\int }_{\mathrm{\Omega }}\frac{1}{2}{\left(\right|\nabla \mathrm{\Phi }|-1)}^2\mathrm{d}\mathrm{\Omega }+\hspace{0.17em}\nu {\int }_{\mathrm{\Omega }}{\delta }_{ϵ}\left(\mathrm{\Phi }\right)\left|\nabla \mathrm{\Phi }\right|\mathrm{d}\mathrm{\Omega }.}$$ (4)

Here, δ(.) is the Dirac function of Φ and g(.) is the edge indicator function in Ref. 20, and I is the CT volume. The initial level-set function representing the aorta boundary is updated at each step t to minimize E according to following update equation that is derived using calculus of variations:

$${\displaystyle \frac{\mathrm{d}}{\mathrm{d}t}\mathrm{\Phi }={\delta }_{ϵ}\left(\mathrm{\Phi }\right)\mathrm{div}\left(g\left(I\right)\frac{\nabla \mathrm{\Phi }}{\left|\nabla \mathrm{\Phi }\right|}\right)+\lambda \left[\mathrm{\Delta }\mathrm{\Phi }-\mathrm{div}\left(\frac{\nabla \mathrm{\Phi }}{\left|\nabla \mathrm{\Phi }\right|}\right)\right]+\hspace{0.17em}\nu {\delta }_{ϵ}\left(\mathrm{\Phi }\right)\mathrm{div}\left(\frac{\nabla \mathrm{\Phi }}{\left|\nabla \mathrm{\Phi }\right|}\right).}$$ (5)

Zero level-set of the final Φ gives us the aorta boundary surface in 3D and Φ ≤ 0 gives us the segmented aorta volume.

After segmentation, we locate a common caudal boundary for the segmented aortas. We use the inferior heart boundary landmark for this purpose. We detect this landmark in a selected coronal slice [Fig. 2(b)]. To find this coronal slice, we use the segmented AA at the axial slice location of the trachea carina. We locate the center of the circular AA cross section and select the coronal slice that passes through this center point. We then detect the inferior heart boundary in this coronal slice using the segmentation of the left lung. The inferior rightmost corner of the left lung at the location of diaphragm and heart boundary is detected. We use this landmark to crop the portion of the aorta below this detected inferior boundary after the segmentation step.

2.C. Aortic calcification detection and extraction of calcification measures

2.C.1. Aortic calcification detection

We detect the calcifications within the segmented aorta volume after we dilate the segmented aorta surface by two voxels to make sure that the calcified plaques located on the aorta wall are included in the segmented aorta region. We then detect the aortic calcifications by applying a threshold value of 130 HU as in Ref. 17 to the segmented aorta volume. Each isolated plaque within the calcified region is extracted with a 3D connected component labeling. However, some of these detected plaques are false positives due to nearby high density regions. These regions are commonly located in two locations: (1) the regions of aortic arch that are close to trachea, where the tracheal calcifications can be misclassified as aortic calcification [Figs. 5(a) and 5(b)] and (2) the regions of DA that are very close to the vertebra, where the vertebral regions can be misclassified as aortic calcification [Figs. 5(c) and 5(d)].

FIG. 5.

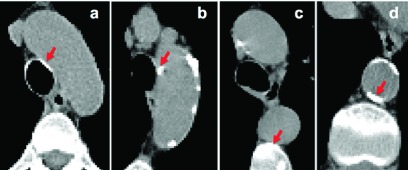
Examples of regions that are true calcifications [(b) and (d)] and false positives [(a) and (c)] after thresholding step. The algorithm further processes these regions and rejects the false positives.

We use the following rules to eliminate false positives: for the plaques close to the trachea boundary, we eliminate the plaque if all of its voxels are located on the trachea wall. For the calcified plaques that are in the posterior part of DA, we apply region growing starting from the detected plaque and check if the plaque is connected to the nearby vertebra region. We eliminate the plaques whose areas grow toward vertebra direction (right posterior direction). See Fig. 6(d) for an example segmented aorta (in red) and detected calcifications (blue).

FIG. 6.

(a) Segmented aorta and extracted centerline (blue). At the location of trachea carina, aorta arch width is measured (black arrow between two yellow circles). (b) Oblique aorta cross sections normal to centerline (green). (c) Axial planes (red) are added for reference. (d) Detected calcifications (blue).

2.D. Calcification measures

We calculate quantitative measures from the detected calcified plaques, which are the number of calcified plaques, the total volume of the plaques, and the 3D Agatston score.²² The original Agatston score²³ was calculated in 2D by multiplying the area of a plaque in a slice with a weighting factor determined by the highest attenuating voxel. The weight was determined from the density value of the maximum density pixel within the detected calcified lesion in a slice. The density values are in Hounsfield units and the weight is set according to that maximum HU value of a plaque. The weight is 1 for 130–199 HU, 2 for 200–299 HU, 3 for 300–399 HU, and 4 for 400 HU and greater. Here, we adapt this 2D measure to 3D. We isolate each plaque in 3D with a 3D connected component labeling algorithm. We calculate plaque volume instead of area, weighted by the highest density voxel of each plaque isolated in 3D. The weight is determined using the same method. This weight is then multiplied by the volume to obtain the 3D Agatston score. In addition to calculating these scores over the entire aorta, we calculated regional measures over descending, arch, and ascending sections of the aorta.

2.E. Extraction of aorta centerline and cross-sectional planes

In order to compute the quantitative measures representing aorta morphology, we first extract the aorta centerline and oblique cross sectional planes normal to the centerline.

2.E.1. Centerline extraction

We extract the centerline of the segmented aorta with a distance transform based skeletonization algorithm.²⁴ This algorithm has a thinness control parameter (th), where a high th value results in a thinner skeleton. We start with a high value (1.0) for a thin centerline but if the complete range of the centerline is not extracted, we iteratively lower the value (by 0.1) until the aorta centerline is completely extracted.

The extracted candidate points need to be ordered before fitting them to a spline to obtain a smooth and continuous centerline curve. We start ordering the candidate points from the most inferior end point (z = 0) and move in superior direction. At each step, from the candidate neighboring points with a larger (smaller for the ascending aorta section) z than current point, we select the one that is closest to the current point. After we reach the top of the arch, we move in inferior direction for the ascending aorta. Finally, a 3D spline curve is fitted to the ordered centerline points and a smooth centerline curve is obtained. An extracted centerline is shown in Fig. 6(a).

2.E.2. Oblique cross-sectional planes’ extraction

After the initial centerline curve c(s) is extracted, the tangent vector at each point along the centerline is calculated and the coordinates of the cross-sectional plane normal to this tangent vector are computed as described in Appendix C [see Figs. 6(b) and 6(c)]. We interpolate the binary segmentation volume at these oblique plane coordinates to obtain the oblique cross section of aorta.

The aorta cross sections in oblique planes are approximately circular. We fit a circle to the aorta boundary points (x, y) in each cross sectional plane and compute the center and the radius of these circles. For circle fitting, we use the following circle equation:

$${\displaystyle x^2+y^2+a\left(1\right)x+a\left(2\right)y+a\left(3\right)=0.}$$ (6)

We solve the following system of linear equations for a:

$${\displaystyle \mathbf{Ka}=\mathbf{b},}$$

where

$${\displaystyle \mathbf{K}=\left(\begin{array}{c}\hfill \mathbf{x}\hspace{0.17em}\hspace{0.17em}\mathbf{y}\hspace{0.17em}\hspace{0.17em}\mathbf{1}\hfill \end{array}\right),\mathbf{b}=-({\mathbf{x}}^2+{\mathbf{y}}^2).}$$ (7)

Here, x and y are vectors of x and y coordinates of boundary points. After calculating a, we compute the circle parameters radius r and center (x_c, y_c),

$${\displaystyle x_c=-\mathbf{a}\left(1\right)/2,}$$

$${\displaystyle y_c=-\mathbf{a}\left(2\right)/2,}$$

and

$${\displaystyle r=\sqrt{(\mathbf{a}{\left(1\right)}^2+\mathbf{a}{\left(2\right)}^2)/4-\mathbf{a}\left(3\right)}.}$$ (8)

The centers of the circles obtained from all the oblique planes are then smoothed by fitting them to a 3D cubic spline function. Similarly, a 3D cubic spline is fitted to the radius values of the obtained circles as well.

2.F. Extraction of aorta morphology features

We extract several quantitative features representing aorta morphology as listed in Table I.

TABLE I.

Aorta morphology features.

Morphology feature	Feature description
Arch width	Distance between DA and AA centers measured at the level of trachea carina
Max arch width	Max distance between DA and AA centers measured around the level of trachea carina
Mean radius	Mean of the oblique aorta cross section radii computed along the aorta, DA, Arch, AA regions
SD radius	Standard deviation of the oblique aorta cross section radii computed along the aorta
Centerline tortuosity	Measure of how much aorta centerline bends computed along the aorta, DA, Arch, AA regions
Centerline curvature	Mean curvature (directional change of the tangent vector) of the centerline curve computed along the aorta, Arch, AA regions

To calculate these features, we use the refined centerline, and the cross-sectional planes extracted normal to this centerline using the approach explained above. We compute the area and radius of aorta cross sections extracted at regular intervals along the centerline curve. The mean and standard deviation of area and radius measures are then calculated over the entire aorta as well as over the regions of aorta which are DA, arch, and AA.

The second set of morphology features are calculated from the aorta centerline. These features include mean curvature and tortuosity of the centerline curve and the width of aortic arch. Curvature measures how sharply a curve bends. The curvature is 0 for a straight line, very small for curves which bend very little, and large for curves which bend sharply. Curvature is measured by the amount that the tangent vector changes direction as we move along the curve. We calculate the curvature over the centerline curve C(t) parametrized with t using the following equation:

$${\displaystyle \kappa =\frac{x^{\prime }\left(t\right)y^{″}\left(t\right)-x^{″}\left(t\right)y^{\prime }\left(t\right)}{{(y^{\prime }{\left(t\right)}^2+x^{\prime }{\left(t\right)}^2)}^{2/3}}.}$$

As a measure of tortuosity, the length of curve divided by the distance between the end points of the curve is often used. However, this measure is not very sensitive to local changes. Therefore, we use the approach suggested in Ref. 25 as a measure of tortuosity. We compute the in-plane and torsional angles between the normal and binormal vectors of the two consecutive points on the centerline. A positive total angle is then calculated at each point by taking the square root of the sum of the squares of the in-plane angle and of the torsional angle. The sum of these angles is computed along the curve and normalized by the curve length. The results are given in rad/cm.

3. RESULTS

In this section, we report how we evaluate the performance of the suggested automated aorta segmentation and calcification detection pipeline in 45 manual segmented CT scans. We further test the algorithm results in a large cohort of 2500 subjects.

3.A. Data set

We test our pipeline using the CT images from the COPDGene study.²⁶ The in-slice image resolutions of the CT volumes are isotropic and in the range of 0.6–0.7mm with a slice thickness that varies between 0.5 and 0.7mm.

Due to presence of noise, we filter the CT images with the anisotropic diffusion filter²⁷ that removes the noise but keeps the high gradient edge locations in the image, such as the aorta wall.

We selected a test set of 50 CT scans on which aorta and aortic calcifications were manually segmented. Forty five scans are used for validation where we evaluate the performance of the proposed segmentation and calcification detection algorithms in comparison to the expert mark-ups. The remaining five CT scans are used to optimize the algorithm parameters. We report these parameters in Table II.

TABLE II.

Values of algorithm parameters.

$d_x^{\mathrm{AA}}$	$d_y^{\mathrm{AA}}$	$d_x^{\mathrm{DA}}$	mI	σI	Δr	Δd	λ	ν
2.2 cm	6.2 cm	5.0 cm	40	23	3 mm	5 mm	0.04	0.2

3.B. Validation of automated aorta segmentation algorithm

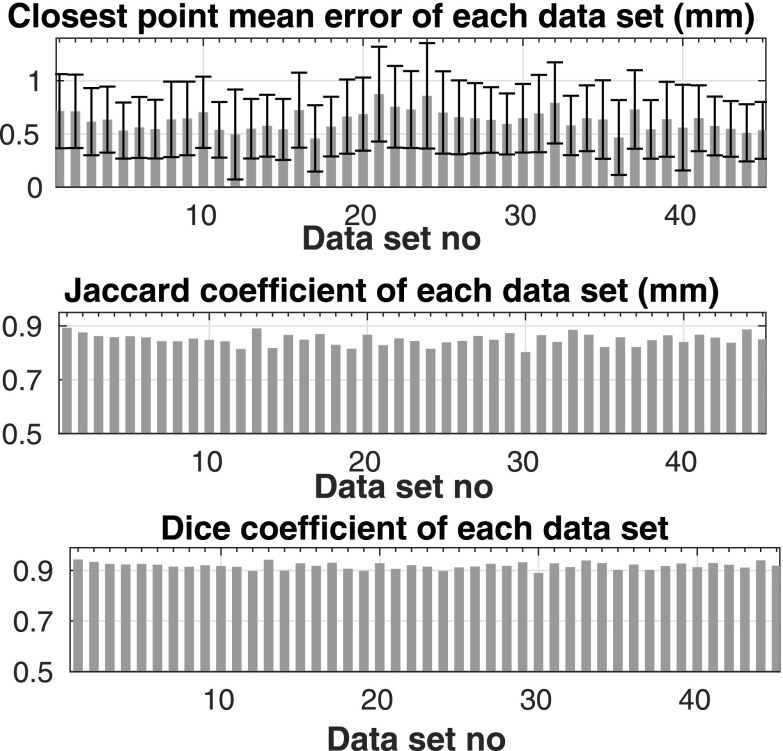
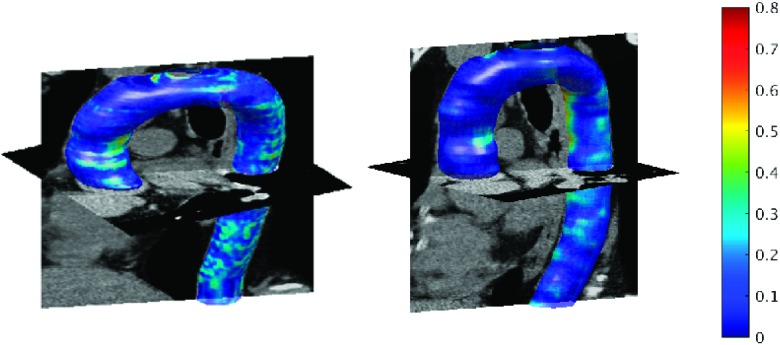
We compute three different metrics to compare the automated segmentation results with the manual segmentations. These metrics are the mean of the point-wise distances, the Jaccard coefficient, and the Dice coefficient. The point-wise distances are calculated as the minimum Euclidean distance between points on manually and automatically segmented surfaces. We report the mean point-wise distance for each subject in Fig. 7(a). The mean of this measure over all 45 subjects was 0.62 ± 0.09 mm for the entire aorta including aortic arch, AA, and DA, 0.61 ± 0.09 mm over DA, and 0.60 ± 0.15 mm over AA. Another similarity metric that we calculated was the Jaccard coefficient, which is given by the intersection of the manually and automatically segmented volumes divided by the union of these volumes. The final metric is the Dice coefficient given by two times the intersection of the manually and automatically segmented volumes divided by the sum of these two volumes. The mean of these measures over all 45 subjects was 0.85 ± 0.02 for Jaccard and 0.92 ± 0.01 for Dice. Figure 7 shows these measures over each data set. The 3D isosurface plot of the segmented aorta is shown in Fig. 8 for two sample CT scans. The colormap indicates the point-wise error between aorta surfaces segmented manually and automatically. The maximum point-wise error (Hausdorff distance) was 0.75 and 0.80 mm, respectively, for these two subjects.

FIG. 7.

Mean ± sd of error (top figure), Jaccard coefficient (middle figure), and Dice coefficient (bottom figure) for each data set.

FIG. 8.

Segmented aorta in 3D for two sample CT scans. Colormap indicates the closest point Euclidean distance (in mm) between automatically segmented and manually labeled aorta surfaces.

3.C. Validation of calcification detection algorithm

We evaluate the calcification detection performance of the algorithm in comparison to the manually detected calcifications. We apply 3D connected component analysis to automatically detected aortic calcifications. We compute false positive (FP), true positive (TP), and false negative (FN) rates for number and volumes of calcifications detected in 45 CT scans. Out of the 424 calcified regions marked by the expert (FN + TP), the algorithm successfully detected 96% correctly ((TP/(FN + TP)) × 100) which is better than 84% rate reported in Ref. 17. The ratio of the successfully detected calcification volume to the volume marked by the expert is 0.92. The ratio of the number of FP calcifications to the number of algorithm detected calcifications (FP/(FP + TP)) is 0.14 and this ratio is 0.08 for the volume of FP calcifications.

3.D. Validation on large cohort

We run the pipeline on the first 2500 subjects of COPDGene study. We used the measures computed from these subjects to further validate the results of the automated aorta morphology measurements with the 2D measurements of aorta radius from the literature. We also report correlations of morphology and size changes with calcification measures and aging.

3.D.1. Average morphology measures

Table III shows the average values of demographic and clinical data over our study group of smokers. The clinical data include pack years of smoking (years of smoking multiplied by the number cigarettes smoked in a day divided by 20), %emphysema in CT (percentage of low attenuating lung regions less than −950 HU in CT) and FEV1% predicted. (FEV1 is the forced expiratory volume in 1 s measured by spirometry and FEV1% predicted is calculated according to prediction equations for the US population. Prediction equations are based on age and height by gender and ethnicity.²⁸) This is a cohort of heavy smokers, with slightly more than half females, and with moderate airflow obstruction measured by FEV1% predicted.

TABLE III.

Mean, standard deviation (sd), and ranges of clinical measures.

	Mean ± sd	Range
Age (yr)	59.76 ± 8.90	45–81
Male (%)	46
Height (cm)	170.41 ± 9.47	141.20–203.20
BMI (kg/m2)	28.66 ± 5.83	15.43–57.90
Pack years of smoking	44.40 ± 24.31	10–216
%Emphysema in CT	5.46 ± 8.80	0.02–60.78
FEV1% predicted	67.21 ± 16.11	19.00–97.00
Body surface area	1.96 ± 0.26	1.27–3.06

We report the mean values of aorta size and morphology measures on all COPD subjects in Table IV. The mean aorta diameter computed by our automated pipeline on GOLD = 0 subjects, with normal lung function, was compared with the result reported in the literature. Most results in the literature were from measurements of aorta radius in a single axial slice while we calculate mean radius along cross sections of the entire aorta. Our results are in the same range with the previously published results on large studies reported using MRI and CT images.^9,29,30 In Framingham heart study (FHS)³⁰ and multi-ethnic study of atherosclerosis (MESA) cohorts,²⁹ a mean AA diameter of 32 mm was reported, while in our measurements we report a mean AA diameter of 31 ± 3 mm. In Ref. 9, a mean DA diameter of 24 ± 3 mm was reported over 1931 subjects, while in our measurements we also report a mean DA diameter of 24 ± 3 mm. We report a mean arch width of 77 ± 11 mm over GOLD = 0 subjects measured at the level where the width is maximum, which we call max arch width in the table. We also report a mean arch width of 70 ± 11 measured at the level of trachea carina, which in the same range of the value of 66 ± 10 for women and 72 ± 11 reported over 108 subjects.

TABLE IV.

First numerical column shows mean and standard deviation (SD) of regional aorta size and morphology measures reported. Second and third numerical columns show Pearson correlation coefficient of these measures with age and body surface area (BSA), respectively.

			Correlation coefficient
Measure	Region	Mean ± SD	Age	BSA
Max arch width (cm)	Arch	7.92 ± 1.17	0.48	0.33
Arch width (cm)	Arch	7.28 ± 1.23	0.45	0.35
Mean radius (cm)	Aorta	1.31 ± 0.13	0.45	0.26
		DA	1.18 ±.13	0.49	0.22
		Arch	1.38 ± 0.13	0.29	0.28
		AA	1.54 ± 0.17	0.32	0.21
	SD radius	Aorta	0.32 ± 0.03	0.43	0.27
Mean tortuosity (rad/cm)	Aorta	2.00 ± 0.42	−0.31	−0.02
		DA	1.21 ± 0.46	−0.06	0.13
		Arch	2.99 ± 1.53	−0.41	−0.31
		AA	2.89 ± 0.90	−0.25	−0.04
	Mean curvature (rad/cm)	Aorta	0.014 ± 0.006	−0.18	0.11
		Arch	0.020 ± 0.009	−0.32	0.03
		AA	0.021 ± 0.015	−0.14	0.05
Log 10 plaque volume (mm3)		Aorta	2.26 ± 1.09	0.63	−0.05
		DA	1.45 ± 1.19	0.51	−0.08
		Arch	1.82 ± 1.18	0.59	−0.05
		AA	1.02 ± 1.15	0.55	−0.07
	Log 10 of num plaques	Aorta	0.77 ± 0.49	0.61	−0.05
Log 10 of sum 3D Agatston	Aorta	3.06 ± 1.44	0.63	−0.07
Log 10 of sum 2D Agatston	Aorta	2.94 ± 1.39	0.63	−0.07

3.D.2. Correlation between morphology measures with calcification measures and age

We report the correlation of aorta calcification and morphology measures with age and body surface area (BSA) in the second and third columns of Table IV. These are the main correlates of the reported measures. There were significant correlations of all measures with age, and some measures with BSA. We then computed pairwise partial Pearson correlation coefficient values between aorta morphology measures and aorta calcification measures after adjusting for age and body surface area. The values in Table V indicate statistically significant correlation values (p < 0.05/m) between most measures even after Bonferroni correction, where m is the number of hypothesis tested (m = 77). The mean aorta radius, arch width, and standard deviation of the radius had a positive correlation with the log transform of the calcification measures. The tortuosity of aorta centerline had a negative correlation with the log transform of the calcification measures.

TABLE V.

Pairwise partial Pearson correlation coefficient values between aorta morphology measures, aorta calcification measures that are adjusted by age and body surface area. The nonempty cells show statistically significant values (p < 0.05/m) after Bonferroni correction, where m = 77 is the number of hypothesis tested.

		Log 10 plaque volume				Log 10 num plaques	Log 10 3D Agatston	Log 10 2D Agatston
All subjects	Region	Aorta	DA	Arch	AA	Aorta	Aorta	Aorta
Max arch width (cm)	Arch	0.10	0.08	0.09	0.13	0.13	0.08	0.08
Arch width (cm)	Arch	0.12	0.09	0.10	0.15	0.16	0.11	0.11
SD radius	Aorta	0.16	0.14	0.10	0.10	0.22	0.14	0.14
Mean radius (cm)	Aorta	0.16	0.15	0.10	0.10	0.23	0.14	0.14
	DA	0.19	0.19	0.13	0.14	0.26	0.17	0.17
	Arch	0.11	0.13			0.18	0.09	0.09
	AA	0.10	0.07			0.14	0.09	0.09
	Mean tortuosity (rad/cm)	Aorta	−0.07	−0.07	−0.08	−0.07
DA
Arch		−0.08		−0.09	−0.08	−0.09	−0.07	−0.07
AA

4. DISCUSSIONS AND CONCLUSIONS

Automatically extracted measures of aorta morphology, size, and calcification have a promising role as potential quantitative biomarkers for various clinical applications. These measures can be used to study age and cardiovascular disease related changes in aorta morphology in smokers. Many recent studies published in the literature show clinical interest in these quantitative measures. However, the commonly reported values of these measures in the clinical literature are from values computed on a single slice and performed by a single expert. Measuring these quantitative values manually is very time consuming, subjective, and prone to error. Available automated techniques require some kind of user interaction to initialize the segmentation pipeline.

In this work, we introduced a fully automated pipeline that first segments the aorta in 3D CT volumes, then detects aorta calcifications, and extracts the aorta centerline and cross sections. Finally, the automated pipeline extracts quantitative features representing aorta size, morphology, and calcification amount. Since all measurements were computed on cross sections of the vessel extracted in 3D, they provide more accurate representation of the vessel cross section.

The validation of the proposed segmentation pipeline against expert segmentations in 45 CT scans indicated that the segmentation algorithm performed well with mean distance error of 0.62 ± 0.09 mm over 45 subjects. The distribution of point-wise segmentation errors was shown for two subjects. The maximum point-wise errors (Hausdorff distances) were less than 0.8 mm, with largest errors occurring in regions where the aorta branches into smaller supra-aortic vessels.

The calcification detection algorithm also performed well and correctly detected 96% of the calcified plaques which is better than the 84% detection rate reported in Ref. 17 over a different data set. However, note that results in Ref. 17 were reported on low-dose CT scans.

For more extensive validations on a larger data set, we applied the fully automated pipeline applied to noncontrast CT images from 2500 smokers from COPDGene study. We compared the averaged measures of descending and ascending aorta diameter and aorta arch width with the values reported in recent studies from the literature. The measures that were computed using the proposed automated pipeline agreed well with the measures reported in the literature.

We found statistically significant associations between aorta morphology and calcification measures. Calcification volume within the aorta was negatively associated with normalized tortuosity of the aorta, but positively associated with the aorta arch width and mean radius of aorta, especially the mean radius of descending aorta. These results may be related to the aorta stiffening as well as unwrapping of arch and the enlargement of aorta cross sections with increasing calcification. Aorta morphology was also highly associated with aging. Aging was positively associated with arch width and mean radius but it was negatively associated with tortuosity and curvature. These are all preliminary results on a COPD cohort of smokers.

The suggested automated pipeline is an objective tool that can be used to assess aorta morphology and aorta calcium plaque on CT scans that will be potentially useful to provide clinically relevant information related to cardiovascular disease in smokers.

One limitation of this study is that our population is from a COPD cohort not a cardiovascular cohort. The reason why we used a COPD cohort is that cardiovascular disease is one of the principal comorbidities in COPD, and, therefore, this is a population with a wide range of diseases that makes it suitable to validate new biomarkers. However, an extensive statistical analysis on a cardiovascular disease cohort needs to be done to draw conclusions from these results.

APPENDIX A: SELECTING THE INITIAL DA AND AA CIRCLES

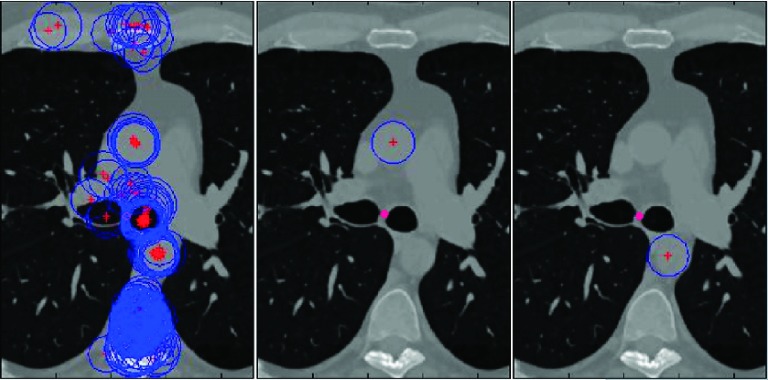
We begin the circle detection process from the axial slice of the main carina and apply circular Hough transform to that slice (see left image in Fig. 9). The search space of circles is limited to the circles with radius from 0.9 to 2.3 cm for DA and 1.5 to 2.9 cm for AA. To select the circles corresponding to DA and AA, we first eliminate some detected circles according to their relative positions with respect to main carina. For AA, we first eliminate the circles which are to the posterior of main carina. We then eliminate circles with a distance from carina larger than $d_x^{\mathrm{AA}}$ and $d_y^{\mathrm{AA}}$ in x (left–right) and y (anterior–posterior) directions, respectively. For DA, we eliminate circles that are inferior to the carina, and the circles with a distance from carina larger than $d_y^{DA}$ in y direction.

FIG. 9.

The left image shows all the detected circles in the slice of main carina, middle and right images show the detected AA and DA circles, respectively. The pink dot shows the location of carina.

From the remaining candidate circles, the one that maximizes an energy function is selected (middle and right images in Fig. 9).

APPENDIX B: SAMPLING OBLIQUE PLANES ALONG THE ARCH

Here, we explain how we sample oblique planes along the arch. The first step is finding the line segment connecting the descending (x_DA = (x₁, y₁, z₁)) and ascending aorta centers (x_AA = (x₂, y₂, z₁)) in the slice of TC. The middle point of this line segment (x_M = ((x₁ + x₂)/2, (y₁ + y₂)/2, 0) is selected and a second line orthogonal to the first one, and passing through this middle point, is found. The slope of second line is then π/2 plus the slope of first line [Fig. 3(a)].

This second line is converted to a plane by sweeping this line along the superior–inferior (z) direction. This gives us a plane that passes through the middle of the arch [vertical plane in Fig. 3(b)]. Rotating this plane around the second line from −90° to +90° with 3° steps, we obtain oblique cross-sectional planes along the half torus shaped arch [oblique planes in Fig. 3(b)].

To implement this rotation around the second line, we first represent the line parametrically, using a unit vector u and a point (x₀) on the line as follows: x(t) = x₀ + tu. Before rotating the points on the vertical plane around vector u, we first translate the points with an amount −s calculated as follows: s = x₀ − 〈x₀, u〉u. We then rotate the points and translate them back using an inverse of the initial transformation matrix for the translation. The overall transformation is given by $\mathbf{T}={\mathbf{T}}_{\mathbf{trans}}^{-1}{\mathbf{T}}_{\mathbf{rot}}{\mathbf{T}}_{\mathbf{trans}}$, where

$${\displaystyle {\mathbf{T}}_{\mathbf{trans}}=\left(\begin{array}{cc}\hfill {\mathbf{I}}_{\mathbf{3}\times \mathbf{3}}\hfill & \hfill -{\mathbf{s}}_{\mathbf{3}\times \mathbf{1}}\hfill \\ \hfill {\mathbf{0}}_{\mathbf{1}\times \mathbf{3}}\hfill & \hfill 1\hfill \end{array}\right).}$$

We compute the rotation matrix using the Rodrigues’ formula for rotating a point around a vector (u). We choose x₀ to be the middle point (x_M), and choose another random point x_P on the line using the line equation. Then, u = (x_P − x₀)/|x_P − x₀|. Using the Rodrigues’ formula, we obtain the rotation matrix R to rotate a point θ degrees around u as follows:

$${\displaystyle \left(\begin{array}{l}{\mathbf{v}}_{\mathbf{1}}\hspace{0.17em}cos\left(\theta \right)+(\mathbf{u}\times {\mathbf{v}}_{\mathbf{1}})sin\left(\theta \right)+〈\mathbf{u},{\mathbf{v}}_{\mathbf{1}}〉(1-cos\left(\theta \right))\mathbf{u}\hfill \\ {\mathbf{v}}_{\mathbf{2}}\hspace{0.17em}cos\left(\theta \right)+(\mathbf{u}\times {\mathbf{v}}_{\mathbf{2}})sin\left(\theta \right)+〈\mathbf{u},{\mathbf{v}}_{\mathbf{2}}〉(1-cos\left(\theta \right))\mathbf{u}\hfill \\ {\mathbf{v}}_{\mathbf{3}}\hspace{0.17em}cos\left(\theta \right)+(\mathbf{u}\times {\mathbf{v}}_{\mathbf{3}})sin\left(\theta \right)+〈\mathbf{u},{\mathbf{v}}_{\mathbf{3}}〉(1-cos\left(\theta \right))\mathbf{u}\hfill \end{array}\right),}$$

where v₁, v₂, and v₃ are the unit vectors in the direction of x, y, and z axis, respectively. The transformation matrix for rotation is then given by

$${\displaystyle {\mathbf{T}}_{\mathbf{rot}}=\left(\begin{array}{cc}\hfill \mathbf{R}\hfill & \hfill {\mathbf{0}}_{\mathbf{3}\times \mathbf{1}}\hfill \\ \hfill {\mathbf{0}}_{\mathbf{1}\times \mathbf{3}}\hfill & \hfill 1\hfill \end{array}\right).}$$

We use the transformation matrix T to rotate all the points within the initial vertical plane to obtain the oblique plane coordinates.

APPENDIX C: TRANSFORMATION MATRIX TO COMPUTE OBLIQUE CROSS-SECTIONAL PLANE

Here, we describe how we sample oblique planes along the aorta centerline curve c(s). First, the tangent vector at each point along the centerline is calculated and the cross-sectional plane normal to the tangent vectors is extracted.

To extract the oblique cross-sectional plane, we first generate coordinates for an axial plane centered at a point s along the centerline. We then rotate this axial plane to obtain the coordinates of the oblique plane using the overall rotation matrix (T_o). To obtain the overall rotation matrix, the inverse of two rotation matrices is multiplied. First, rotation matrix (T_xy) rotates the tangent vector t = [u v w] into xz-plane and the second rotation matrix (T_z) rotates it further to the z-axis direction. Applying the inverse of these transformations to the axial plane coordinates (T_o = T_xy⁻¹T_z⁻¹) with a normal vector pointing in z direction rotates them such that the obtained oblique plane has normal vector in the direction of the tangent vector t,

$${\displaystyle {\mathbf{T}}_{\mathbf{xy}}=\left(\begin{array}{cccc}\hfill cc\hfill & \hfill ss\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill -ss\hfill & \hfill cc\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill \end{array}\right),\begin{array}{l}cc=\frac{u}{\sqrt{u^2+v^2}},\hfill \\ ss=\frac{v}{\sqrt{u^2+v^2}},\hfill \end{array}}$$

$${\displaystyle {\mathbf{T}}_{\mathbf{z}}=\left(\begin{array}{cccc}\hfill dd\hfill & \hfill 0\hfill & \hfill -ee\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill ee\hfill & \hfill 0\hfill & \hfill dd\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill \end{array}\right),\begin{array}{c}\hfill dd=\frac{w}{\sqrt{u^2+v^2+w^2}},\hfill \\ \hfill ee=\frac{\sqrt{u^2+v^2}}{\sqrt{u^2+v^2+w^2}}.\hfill \end{array}}$$ (C1)