Adapt-Mix: learning local genetic correlation structure improves summary statistics-based analyses

Abstract

Motivation: Approaches to identifying new risk loci, training risk prediction models, imputing untyped variants and fine-mapping causal variants from summary statistics of genome-wide association studies are playing an increasingly important role in the human genetics community. Current summary statistics-based methods rely on global ‘best guess’ reference panels to model the genetic correlation structure of the dataset being studied. This approach, especially in admixed populations, has the potential to produce misleading results, ignores variation in local structure and is not feasible when appropriate reference panels are missing or small. Here, we develop a method, Adapt-Mix, that combines information across all available reference panels to produce estimates of local genetic correlation structure for summary statistics-based methods in arbitrary populations.

Results: We applied Adapt-Mix to estimate the genetic correlation structure of both admixed and non-admixed individuals using simulated and real data. We evaluated our method by measuring the performance of two summary statistics-based methods: imputation and joint-testing. When using our method as opposed to the current standard of ‘best guess’ reference panels, we observed a 28% decrease in mean-squared error for imputation and a 73.7% decrease in mean-squared error for joint-testing.

Availability and implementation: Our method is publicly available in a software package called ADAPT-Mix available at https://github.com/dpark27/adapt_mix.

Contact: noah.zaitlen@ucsf.edu

1 Introduction

Summary statistics of association tests, such as effect size estimates and their standard errors, are becoming the datatype of choice in many genetic analyses due to two significant advantages. First, summary statistics-based methods are generally orders of magnitude faster than their genotype-based counterparts. The rapidly increasing size of existing and planned cohorts is causing computational bottlenecks for some standard analyses. Second, analyses of summary statistics are often a necessity since access to individual-level data is complicated by privacy and other issues (Gymrek et al.., 2013). Publication of summary statistics is now required for all Nature Genetics genome wide association study (GWAS) papers, and these statistics have already been released for a large number of traits. For these reasons, a growing number of summary statistics-based methods, including imputation of z-scores, joint-testing, fine mapping of causal variants, quality control of GWAS results and gene-based tests, have recently been published (Bulik-Sullivan et al., 2014; Han et al., 2011; Hormozdiari et al., 2014; Kichaev et al., 2014; Liu et al., 2010; Pasaniuc et al., 2014; Yang et al., 2012). Moving forward, the integration of summary statistics will be vital for increasing our knowledge of various complex diseases and phenotypes (Schork et al.., 2013).

Summary statistics-based methods typically require estimates of linkage-disequilibrium (LD) between markers as input. Existing tools use ‘best guess’ reference panels to estimate LD (Han et al., 2011; Kichaev et al., 2014; Pasaniuc et al., 2014; Yang et al., 2012). For example, Yang et al. (2012) used European ancestry individuals from the Queensland Institute of Medical Research reference panel to estimate LD for an analysis of statistics produced from the European ancestry GIANT consortium (Speliotes et al.., 2010). This approach is not optimal and has the potential to produce misleading results in the case of admixed populations. Admixed individuals’ genomes can be viewed as mosaics, where different segments of the genome are derived from various ancestral groups. Previous work has shown that the proportions of ancestry for individuals from admixed populations are highly variable (Bryc et al., 2010; Silva-Zolezzi et al., 2009; Wang et al., 2008). Given this high variability in admixed populations, ‘best guess’ panels are more likely to have LD estimates that are not in concordance with original datasets and which vary in their local structure. This will be especially true if the population of interest has no reference panel available. Furthermore, several genotype-based methods have shown that learning local structure from multi-population reference panels improves performance even in the case of homogenous study populations (Howie et al., 2009; Pasaniuc et al., 2013).

In this work, we develop a method, Adapt-Mix, to accurately estimate the local single-nucleotide polymorphism (SNP) correlation matrix for each region of the genome from summary statistics of an arbitrary population study. We compute the correlation matrix using a mixture of existing reference panels, such as the 1000 Genomes Project Consortium (2012), where the mixture proportion for each reference population is learned from summary statistics. Unlike previous approaches, our method incorporates data from multiple reference panels when computing the correlation matrix and allows for adaptation to local structure. We first provide a closed form solution for the expected correlation structure from a mixture of populations in a genomic locus. Then, using this derivation, we efficiently search for the mixture of populations in each genomic locus that maximizes/minimizes an objective function most relevant to the problem in question. For example, in this work, we consider the problems of imputation and joint-testing from summary statistics, using imputation error and joint-test accuracy as the objective function, respectively. In practice, arbitrary objective functions can be used provided they can be computed efficiently.

We apply our method to summary statistics from simulated phenotypes over real genotypes from the Genes-environments & Admixture in Latino Americans (GALA II, Borrell et al.., 2013) cohort that is composed of Mexican and Puerto Rican individuals. We also apply our method to real coronary artery disease summary statistics from the CARDIoGRAMplusC4D consortium (Coronary Artery Disease (C4D) Genetics Consortium, 2011; Schunkert et al.., 2011). In the simulated datasets, we show significant improvements in the mean-squared error (MSE) of our mixture correlation coefficients compared with the most relevant reference panels. We also demonstrate the direct impact of the improved correlation estimates for imputation and joint-testing methods, which take correlation matrices as input. For both the simulated summary statistics over the GALA II study as well as the meta-analysis results, we show significant improvement in both summary statistics-based imputation and joint-testing (Pasaniuc et al.., 2014; Yang et al.., 2012).

2 Methods

First, we describe the situation where Adapt-Mix may be applied. We then derive a formula for the genotype correlation matrix as a mixture of several reference populations and describe our procedure for optimizing the mixture frequencies for various objective functions. We end the section by discussing the simulation framework in which we evaluate our method.

GWAS summary statistics typically consist of an effect size β_i and standard error σ_i for each SNP i examined in a study. For simplicity, β_i and σ_i can be converted to a Wald test statistic (Z-score) z_i. When dealing with case–control phenotypes $z_i=\sqrt{N}\frac{p_i^{+}-p_i^{-}}{\sqrt{2p_i(1-p_i)}}$, where N is the sample size, $p_i^{+}$ ($p_i^{-}$) is the frequency of the reference allele in cases (controls), and p_i is the overall frequency. For quantitative phenotypes $z_i=\sqrt{N}\text{cor}(\overrightarrow{g_i},\overrightarrow{q})$, where $\overrightarrow{g_i}$ are the genotypes of the individuals and $\overrightarrow{q}$ are the phenotypes. Here, $\overrightarrow{g_i}=\left\{g_{i1}\mathrm{...}{g}_{iN}\right\}$ for $g_{id}\in \{0,1,2\}$, g_id being the count of the reference allele for individual d.

As input, most summary statistics-based methods take Z-scores and a correlation matrix Σ (Bulik-Sullivan et al., 2014; Han et al., 2011; Hormozdiari et al., 2014; Kichaev et al., 2014; Liu et al., 2010; Pasaniuc et al., 2014; Yang et al., 2012). For each pair of SNPs i, j, the correlation matrix has the value ${\Sigma }_{ij}=r_{ij}$, where r_ij is the Pearson correlation coefficient between the SNPs in the study. If individual level genotypes are available, the correlation can be computed by $r_{ij}=\text{cor}(\overrightarrow{g_i},\overrightarrow{g_j})$. When individual level genotypes are unavailable, r_ij is typically estimated using a reference panel of genotypes from a population similar to the source population of the data being analyzed. In this work, we develop a method to provide a better estimate of r_ij using a combination of reference panels from different populations. Given a set of K reference populations, we generate a correlation matrix for each genomic locus using a new mixture population, where the frequency of population $k\in K$ in the mixture population is f_k. The objective of our work is to select the frequencies, f_k, that optimizes the performance of the summary statistics method of interest.

2.1 Estimating the mixture correlation matrix

Given a set of mixture frequencies, $\overrightarrow{f}=\{f_1,\dots ,f_K\}$, where $f_k\in \overrightarrow{f}$ is the frequency for population $k\in K$. We wish to compute the expected correlation between each pair of SNPs in the mixture population. For simplicity, we begin by deriving the mixture variance of the allele frequencies (${\sigma }_i^2$) at SNP i, in a mixture population composed of two reference populations. At SNP i, the two reference populations will have separate variances (${\sigma }_{1i}^2,{\sigma }_{2i}^2$), sample sizes (n₁, n₂) and allele frequencies ($p_{1i},p_{2i}$).

Additionally, assume that each reference population has a mixture frequency equal to their proportion of sample size, i.e. $f_1=\frac{n_1}{n_1+n_2}$ and $f_2=\frac{n_2}{n_1+n_2}$. We can then express the mixture variance as

$${\sigma }_i^2=\frac{\sum _{z=1}^{n_1}{(g_{1z}-2p_i)}^2+\sum _{q=1}^{n_2}{(g_{2q}-2p_i)}^2}{(n_1+n_2)}$$

where g_kd is the genotype of individual d in population k, and $2p_i=f_{1}2p_{1i}+f_{2}2p_{2i}$ is the genotype frequency in the mixture population. Let us now consider only ${\sum }_{z=1}^{n_1}{(g_{1z}-2p_i)}^2$. This term is equal to

$$\begin{array}{l}\sum _{z=1}^{n_1}{[(g_{1z}-2p_{1i})+(2p_{1i}-2p_i)]}^2\\ =\sum _{z=1}^{n_1}{(g_{1z}-2p_{1i})}^2+n_1{(2p_{1i}-2p_i)}^2=n_1{\sigma }_{1i}^2+n_1{(2p_{1i}-2p_i)}^2\end{array}$$

Applying the same logic to ${\sum }_{q=1}^{n_2}{(g_{2q}-2p_{2i})}^2$, we arrive at the formula for the variance for the mixture population.

$$\begin{array}{c}{\sigma }_i^2=\frac{n_1{\sigma }_{1i}^2+n_2{\sigma }_{2i}^2}{n_1+n_2}+\frac{n_1{(2p_{1i}-2p_i)}^2+n_2{(2p_{2i}-2p_i)}^2}{n_1+n_2}\\ =f_1{\sigma }_{1i}^2+f_1{(2p_{1i}-2p_i)}^2+f_2{\sigma }_{2i}^2+f_2{(2p_{2i}-2p_i)}^2\end{array}$$

We now extend from 2 to K populations. Suppose we have a set of reference panels representing K populations and their corresponding mixture frequencies, $\overrightarrow{f}$. Then for SNP i in population $k\in K$, let ${\sigma }_{ki}^2$ be the variance and $2p_{ki}$ be the frequency. The frequency in the mixture population is then $2p_i={\sum }_{k=1}^K{f}_{k}2p_{ki}$ and the combined variance at SNP i is

$$\begin{array}{r}{\sigma }_i^2=f_1\sum _{z=1}^{n_1}{(g_{1z}-2p_i)}^2+\cdots +f_K\sum _{l=1}^{n_K}{(g_{Kl}-2p_i)}^2\\ =f_1{\sigma }_{1i}^2+f_1{(2p_{1i}-2p_i)}^2+\cdots +f_K{\sigma }_{Ki}^2+f_K{(2p_{Ki}-2p_i)}^2\\ =\sum _{k=1}^K{f}_k[{\sigma }_{ki}^2+4{(p_{ki}-p_i)}^2]\end{array}$$ (1)

Next, we derive the covariance between SNPs i and j in the mixture population. If x and y are random variables, ${\sigma }_{x+y}^2=cov(x+y,x+y)=cov(x,x)+cov(y,y)+cov(y,x)+cov(x,y)={\sigma }_x^2+{\sigma }_y^2+2cov(x,y)$ and thus $cov(x,y)=\frac{{\sigma }_{x+y}^2-{\sigma }_x^2-{\sigma }_y^2}{2}$

Let $co{v}_k(i,j)$ be the covariance of SNPs i and j in population k. Then the covariance in the mixture population is:

$$\begin{array}{r}2cov{(i,j)}_{i\ne j}=\left[{\sigma }_{i+j}^2-{\sigma }_i^2-{\sigma }_j^2\right]\\ =\sum _{k=1}^K{f}_k\{\left[{\sigma }_{ki}^2+{\sigma }_{kj}^2+2co{v}_k(i,j)+4{(p_{k(i+j)}-p_{(i+j)})}^2\right]\\ -\left[{\sigma }_{ki}^2+4{(p_{ki}-p_i)}^2]-[{\sigma }_{kj}^2+4{(p_{kj}-p_j)}^2\right]\}\\ =\sum _{k=1}^K{f}_k\{\left[{\sigma }_{ki}^2+{\sigma }_{kj}^2+2co{v}_k(i,j)+4{((p_{ki}-p_i)+(p_{kj}-p_j))}^2\right]\\ -\left[{\sigma }_{ki}^2+4{(p_{ki}-p_i)}^2\right]-\left[{\sigma }_{kj}^2+4{(p_{kj}-p_j)}^2\right]\}\\ \Rightarrow cov{(i,j)}_{i\ne j}=\sum _{k=1}^K{f}_k\left[{cov}_k(i,j)-4(p_{ki}-p_i)(p_{kj}-p_j)\right]\end{array}$$

By definition, the mixture correlation matrix is

$${\Sigma }_{ij}=\frac{cov(i,j)}{\sqrt{{\sigma }_i^2{\sigma }_j^2}}$$ (2)

Algorithm 1 details our procedure for computing the mixture correlation matrix over a set of SNPs. Given K populations and M SNPs, it takes as input the mixture frequencies ($\overrightarrow{f}$), a matrix of SNP variances (${\mathbf{V}}_{K\text{x}M}=\left\{{\sigma }_{ki}\right\}$), a matrix of the pairwise SNP covariances (${\mathbf{C}}_{K\text{x}M\text{x}M}=\{co{v}_k(i,j)\}$) and a matrix of the genotype frequencies (${\mathbf{P}}_{K\text{x}M}=\left\{2p_{ki}\right\}$) and outputs the mixture correlation matrix.

Algorithm 1 Create Σ.

Input: $\overrightarrow{f}$, V, C, P

Output: Σ

 # Normalize mixture freqs. so they sum to 1

 $\overrightarrow{f}$ = $\overrightarrow{f}/sum(\overrightarrow{f})$

 # Compute adjustment factors for mixture variances

 WeightedGT = P $({\overrightarrow{f}}^{\text{T}})$,

 NegWeightedGT = P $[{(\overrightarrow{f}-1)}^{\text{T}}]$

 D = empty K x M matrix

 for all k in $\left\{\mathrm{1...}K\right\}$ do

   D_k = NegWeightedGT_k + sum(WeightedGT_l), $\forall l\ne k$

 # Compute mixture variances

 $MixVar=(D^2+\mathbf{V})$

 # Compute mixture covariances

 MixCov = empty K x M x M matrix

 for all k in $\left\{\mathrm{1...}K\right\}$ do

  $tmp=f_k*({\mathbf{C}}_k+[D_k\otimes D_k])$

  MixCov $\text{=}$ $C+tmp$

# Compute mixture correlations

denominators $=\sqrt{(MixVar\otimes MixVar)}$, ▹Square-root applied element-wise

$\Sigma =MixCov/\text{denominators}$ ▹ Element-wise division

2.2 Optimization of mixture frequencies

Given this algorithm for computing the correlation matrix Σ of the mixture population over a set of SNPs, we turn to the problem of selecting the mixture frequencies $\overrightarrow{f}$. We formulate this as a constrained optimization problem: minimizing (or maximizing) the value of a given objective function subject to the constraint that $\sum f=1$ using the L-BFGS algorithm (Byrd et al.., 2006). In this context, the ‘best guess’ approach corresponds to setting f_k = 1 for the guessed population and f_j = 0 $\forall j\ne k$. In this work, we consider the problems of imputation and joint-testing from summary statistics and therefore selected the MSE of imputed z-scores at observed SNPs and MSE of computed joint-test statistics as our objective functions, respectively (see Sections 2.3 and 2.4). However, other objective functions may be more appropriate depending on the purpose of the summary statistics-based method. For example, one could chose to maximize the likelihood of the observed z-scores $\overrightarrow{Z}$ under a multivariate normal distribution.

To allow for variation in local correlation structure, the genome is separated into W equally sized non-overlapping windows. For each window, $w\in \left\{\mathrm{1...}W\right\}$, we compute the correlation matrix using only SNPs in w, ${\Sigma }^{(w)}$. Using ${\Sigma }^{(w)}$, z-scores are imputed for all SNPs in w and the imputed values are used to compute the MSE from the true z-scores. We exclude SNPs from ${\Sigma }^{(w)}$ with a minor allele frequency (MAF) less than 0.01 in any of the k populations, missing z-scores, $r^2\le 0.003$, or an undefined r with the SNP we are imputing. These SNPs are excluded because they only add noise to the imputation process. To ensure that Σ is invertible, λ is added to the diagonal of the matrix. The final correlation matrix is then $\Sigma ={\Sigma }^{\text{unadj}}+\lambda I$. ${\Sigma }^{\text{unadj}}$ is the original correlation matrix prior to adding λ. The exact algorithm to compute the imputation MSE for a set of SNPs in a window is described in Algorithm 2.

Algorithm 2 MSE objective function.

Input: $\overrightarrow{f}$, V, C, P, windowSize, λ, $\overrightarrow{Z}$

Output: meanSquaredError

 # Normalize mixture freqs. so they sum to 1

 $\overrightarrow{f}$ = $\overrightarrow{f}/sum(\overrightarrow{f})$

 # Compute number of windows

 $windows=length(\overrightarrow{Z})/\text{windowSize}$

 # Initialize numerator and denominator of MSE

 numerator = 0

 denominator = 0

 for all $q\in \left\{\mathrm{1...}m\right\}$ do

  # Compute Sigma using SNPS in window q

   ${\Sigma }^{(q)}=\text{Create}\Sigma (\overrightarrow{f},V^{(q)},C^{(q)},P^{(q)})$, see Algorithm 1

   ${\Sigma }^{(q)}={\Sigma }^{(q)}+\lambda I$

  # Impute SNPs in the window

  for all $s\in \left\{\mathrm{1...}\text{windowSize}\right\}$ do

   $z_s={\Sigma }_{st}^{(q)}{[{\Sigma }_{tt}^{(q)}]}^{-1}{\overrightarrow{Z}}_t^{(q)},\forall t\ne s$

   $numerator=numerator+{(z_s-{\overrightarrow{Z}}_s^{(q)})}^2$

   $denominator=denominator+1$

meanSquaredError = numerator / denominator

The procedure we have described is easily extendable from a window to any region, be it a whole-genome, chromosome or single locus. In this case, $\overrightarrow{f}$ is optimized by minimizing/maximizing the objective function over the sum of the non-overlapping windows. If there are a large number of SNPs in the region of interest, the convergence time of the algorithm will increase. To minimize the computation time when optimizing over the entire genome, we selected regions of the genome that have the largest absolute z-scores. Specifically, for every set of five adjacent windows, we optimized using the two windows with the largest number of z-scores with >1.5.

2.3 Imputation

The z-score at a SNP i can be imputed from summary statistics and the correlation matrix, Σ, using the ImpG approach (Pasaniuc et al.., 2014). Pasaniuc et al. used a Gaussian approximation combined with a windowing approach to impute the z-score at i. The windowing aims to decrease runtime and reduce statistical noise that might be caused by distant SNPs with random non-zero correlation but no true LD. Define $\overrightarrow{Z_t}$ as the set of observed z-scores within a given window size around i. The imputed z-score is then $z_i={\Sigma }_{it}{\Sigma }_{tt}^{-1}\overrightarrow{Z_t}$ for all SNPs t in the window.

2.4 Joint-testing

At genomic loci where two SNPs are negatively correlated, using a marginal test often underestimates effect sizes (Galarneau et al., 2010; Sanna et al., 2011; Yang et al., 2012). A joint analysis is more powerful than a marginal test when analyzing such SNPs. Given two z-scores computed at SNPs i and j using a marginal test, a ${\chi }^2$ test-statistic with 2 degrees of freedom, J_ij can be calculated as shown in Equation (3).

$$J_{ij}=\frac{1}{1-{\Sigma }_{ij}^2}(z_i^2+z_j^2-2{\Sigma }_{ij}{z}_i{z}_j)$$ (3)

In our tests, the calculation of J_ij is restricted to SNPs that have a pairwise correlation $\left|r\right|<0.8$ because small changes in r can cause large fluctuations in J_ij as $\left|r\right|$ approaches 1.

2.5 Simulation framework

We simulated data using individuals from the Genes-environments & Admixture in Latino Americans (GALA II) cohort (Borrell et al.., 2013), which is composed of 1245 Mexican and 1785 Puerto Rican individuals. The Mexican individuals have predominantly European and Native American ancestry, whereas their Puerto Rican counterparts tend to have mostly European and African ancestry. We conducted separate simulations for each group due to the differences in ancestry. We generated quantitative phenotypes and z-scores for every non-overlapping window of 1000 SNPs. For each window, a binomial trial (P = 0.01) was used to determine whether the phenotype should be drawn from the null or alternate. Under the null, individuals’ phenotypes were drawn from a $\mathcal{N}(0,1)$. Under the alternate, we assumed an effect size of 0.2 and drew individuals’ phenotypes from $\mathcal{N}(0.2g_{id},1)$, where g_id is the genotype of individual d at SNP i. The phenotypes were generated using the SNP in the middle of each window, and z-scores were computed at all SNPs as described in the introduction of Section 2.

2.6. Reference panels

Reference panels were generated using the 1000 Genomes (1KG) Phase 3 data from the following 11 populations: CEU, IBS, FIN, GBR, TSI, YRI, MXL, PUR, CHB, JPT and GIH. For each dataset we analyzed (i.e. GALA II, CARDIoGRAMplusC4D), we removed any A/T and G/C SNPs to avoid strand issues. We then took an intersection of rsids between our data and the 1KG data to determine which SNPs to include in our reference panels. All SNPs for the reference panels were coded as the number of reference alleles an individual had (i.e. 0, 1 and 2).

3 Results

We applied Adapt-Mix to summary statistics from simulated and real data to estimate the pairwise SNP correlation matrix (Σ). In this work, we use z-score imputation and joint-testing. For both datasets, we used several approaches to estimate Σ and impute z-scores. All imputation was done using a window size of 200 SNPs and $\lambda =0.1$. The values for window size and λ were chosen based on the recommended settings used in Pasaniuc et al. (2014). We measured the impact of using different methods to estimate Σ on z-score imputation by computing the MSE and Pearson correlation coefficient (r) between the imputed z-scores and true z-scores. In addition to imputation, we also performed joint-testing in the simulated data because we had access to the individual genotypes and thus they could compute the true SNP correlation matrix. Again, we measured the effect of several Σ estimation methods on joint-testing by computing the MSE and r between the true joint statistics and the estimated joint statistics.

3.1 Simulated data

Simulated z-scores from the GALA II genotypes (see Section 2.5) were used to determine whether our method gave more accurate results for (i) imputing z-scores and (ii) computing joint-test statistics. Since there are multiple ways to optimize mixture frequencies using Adapt-Mix, we compared the use of several optimization strategies against the ‘best guess’ approach. Using Adapt-Mix, we estimated Σ using 1KG reference panels by optimizing over each chromosome (1KG-Chrom), over the whole genome (1KG-Genome) and per window (1KG-Window). We note that any SNP used to measure imputation quality was excluded during optimization. Additionally, to evaluate how our method affects imputation and joint-testing when a ‘best guess’ panel is unavailable, we removed both MXL and PUR panels and optimized frequencies over the chromosomes (1KG-No-PUR-MXL).

3.1.1 Population Frequencies

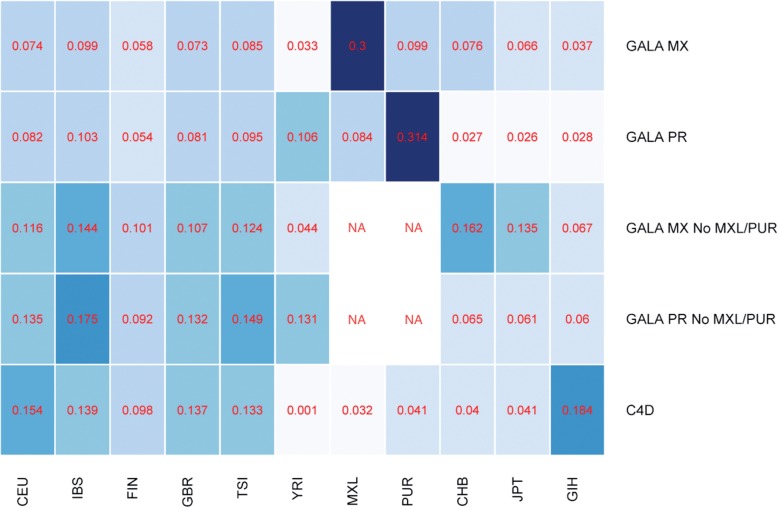
We applied our method to simulated data over Mexican and Puerto Rican individuals from the GALA II cohort (Borrell et al.., 2013). Figure 1 shows the average frequency assigned to each population when frequencies were optimized per chromosome. When matching reference populations are included in the optimization (MXL for the Mexicans and PUR for the Puerto Ricans), nearly one-third of the mixture is assigned to the matching reference panel. The rest of the frequencies are distributed to populations in a similar manner to the admixture proportions of each group (Baran et al.., 2012). Having predominantly Native American and European ancestry, Mexicans have frequencies distributed among European and East Asian panels in addition to MXL. However, when MXL and PUR are not included, we see an increase in frequency assigned to the East Asian panels. Puerto Ricans have more African ancestry than Native American ancestry, and we observe a correspondingly larger frequency of the YRI (African) panel and lower frequencies of East Asian panels.

Fig. 1.

This heatmap shows the average mixture frequency assigned to each reference population when optimizing over independent chromosomes for various datasets

3.1.2 Imputation

We next evaluated the imputation performance of the different approaches to estimating Σ. We measured each method’s impact on imputation by computing the MSE and Pearson correlation coefficient (r) between the imputed z-scores and true z-scores. We imputed the z-score of the 100th SNP in every window. We restricted our analysis to SNPs with an MAF $\ge$ 0.01 in the reference panel since imputation quality tends to be poor for rare SNPs. We also removed from Σ SNPs that had a $r^2\le 0.003$ with the SNP we were imputing. When using a mixture reference panel, we filtered SNPs using a mixture MAF. The mixture MAF for SNP i is ${\sum }_{k=1}^K{f}_k{\text{MAF}}_{ki}$, where f_k is the mixture frequency assigned to population k and MAF_ki is the MAF of SNP i in k.

As the gold standard, the original GALA II genotypes were used to estimate Σ. It is clear from Tables 1 and 2 that using the original genotypes results in very high imputation quality. To demonstrate that using the wrong reference panel can cause a huge decrease in performance, we imputed z-scores using YRI and JPT as reference panels for the Mexicans and Puerto Ricans, respectively. Using the wrong reference panel resulted in MSE increasing over 400% in the Mexicans and over 250% in the Puerto Ricans.

Table 1.

Performance of each reference panel when imputing z-scores for GALA II Mexicans

Panel	n	MSE	r
GALA II	2966	0.214	0.916
YRI	2572	1.11	0.499
MXL	2923	0.615	0.737
1KG-Genome	2836	0.484	0.807
1KG-Chrom	2898	0.451	0.818
1KG-Window	2836	0.438	0.824
1KG-No-MXL-PUR	2904	0.507	0.795

Table 2.

Performance of each reference panel when imputing z-scores for GALA II Puerto Ricans

Panel	n	MSE	r
GALA II	3231	0.234	0.903
JPT	2572	0.884	0.626
PUR	3103	0.554	0.757
1KG-Genome	2759	0.587	0.760
1KG-Chrom	2906	0.473	0.800
1KG-Window	2839	0.467	0.804
1KG-No-MXL-PUR	2912	0.520	0.795

Next, z-scores were imputed using Adapt-Mix to estimate LD. We found that for imputation in admixed individuals, locally optimizing mixture frequencies over each window performs the best. For z-scores imputed over the whole genome, there is a 28.8% decrease in MSE for the Mexicans and a decrease of 15.7% for the Puerto Ricans (Tables 1 and 2). Similar decreases in MSE are seen when optimizing frequencies over the chromosome and the entire genome. Even when MXL and PUR were removed, we see that our method approach to estimating Σ outperforms the ‘best guess’ panel. We also see increases in the r of imputed and true z-scores in the Mexicans and the Puerto Ricans when using Adapt-Mix. The increase in r is equivalent to an increase of 25.0% and 12.8% in effective sample size for the Mexicans and Puerto Ricans, respectively. Interestingly, the local optimization approach does not necessarily find mixture frequencies that are closest to the study’s overall mixture of ancestry. The results here indicate that using such a mixture may not be the best for imputation accuracy and highlights the benefits of using the correct objective function when optimizing mixture frequencies for the selected summary statistics-based method.

3.1.3 Joint-test

Joint-testing of pairs of SNPs from summary statistics also relies on estimates of the pairwise correlation between SNPs (Yang et al.., 2012). Using SNPs on chromosome 22, we computed true joint statistics using Σ computed from the genotypes of the GALA II individuals. The estimated joint statistics were computed using Σ estimated using Adapt-Mix. The mixture frequency optimization strategies were the same as those used in z-score imputation. We computed Joint statistics for SNPS that had a MAF or mixture MAF $\ge 0.05$ in all of the Σ estimation approaches. Tables 3 and 4 show that using a Σ estimated from a mixture reference panel results in increased performance over using a ‘best guess’ reference panel.

Table 3.

Performance of each panel for the joint statistics on chromosome 22 of the GALA II Mexicans (n = 41 758)

Panel	MSE	r	Mean diff.	Var. of diff.
MXL	0.116	0.988	0.042	0.114
1KG-Chrom	0.031	0.997	0.004	0.031
1KG-Genome	0.048	0.995	0.008	0.048
1KG-Window	0.05	0.994	0.006	0.049
1KG-No-MXL-PUR	0.057	0.994	0.005	0.057

Table 4.

Performance of each panel for the joint statistics on chromosome 22 of the GALA II Puerto Ricans (n = 43 715)

Panel	MSE	r	Mean diff.	Var. of diff.
PUR	0.057	0.994	0.023	0.057
1KG-Chrom	0.017	0.998	0.004	0.017
1KG-Genome	0.070	0.993	0.018	0.069
1KG-Window	0.042	0.995	0.012	0.042
1KG-No-MXL-PUR	0.032	0.997	0.008	0.032

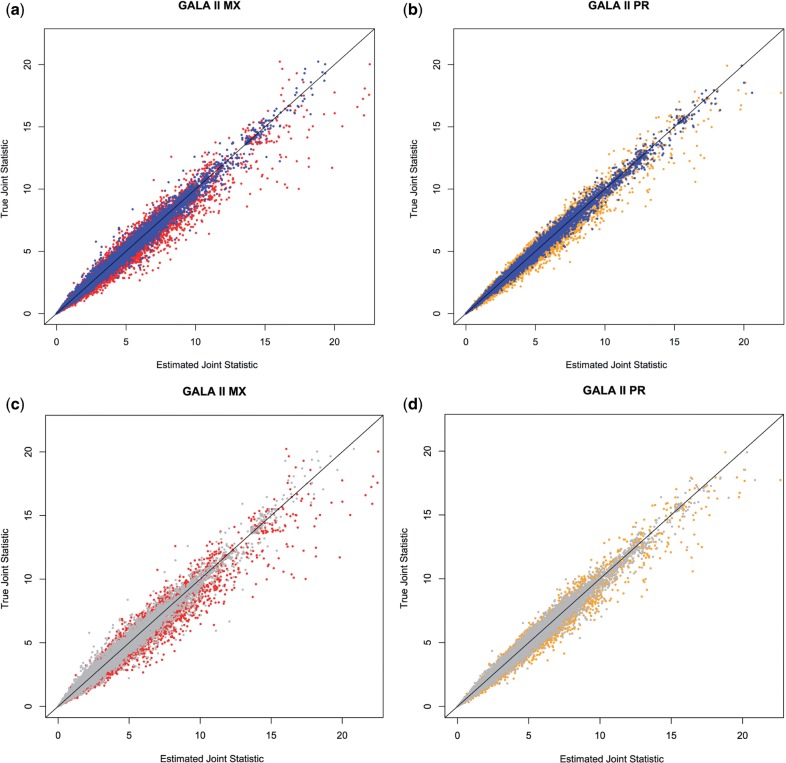
In both populations, the frequencies optimized per chromosome (1KG-Chrom) performed the best. Compared with using a ‘best guess’ panel, we observed a 73.7% decrease in MSE for the Mexicans and a 70.2% decrease in MSE for the Puerto Ricans. We plotted the estimated joint statistics versus the true joint statistics for Mexicans and Puerto Ricans for different choices of Σ (Fig. 2). The results show that joint statistics computed using the combined reference panel are in higher concordance with the truth than the ‘best guess’ panel. Remarkably, even when MXL and PUR are removed from the mixture, estimates of Σ improvements can be clearly seen (Fig. 2c and d).

Fig. 2.

Estimated joint statistic (x axis) versus the true joint statistic (y axis) in the GALA II individuals using Σ estimated from a ‘best guess’ reference panel and Adapt-Mix. (a) Joint statistics for the GALA II Mexicans using MXL (red) and 1KG-Chrom (blue). (b) Joint statistics for the GALA II Puerto Ricans using PUR (orange) and 1KG-Chrom (blue). (c) Joint statistics for the GALA II Mexicans using MXL (red) and 1KG-No-MXL-PUR (gray). (d) Joint statistics for the GALA II Puerto Ricans using PUR (orange) and 1KG-No-MXL-PUR (gray)

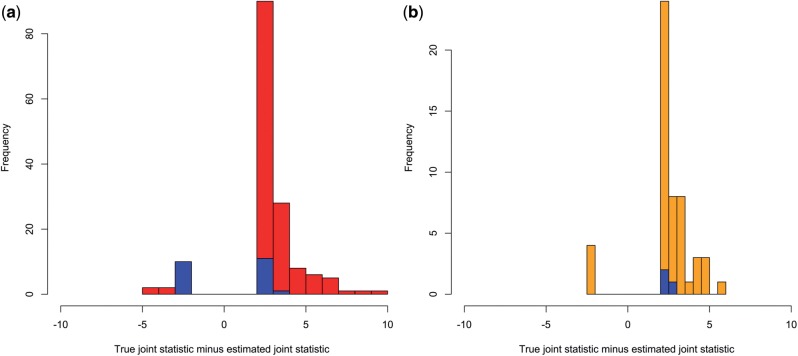
To show that the joint statistics produced by using our method for estimating correlations are unbiased (i.e. E[J_ij − $\widehat{J_{ij}}$] = 0), we looked at the mean difference between the true statistics and estimated statistics. Tables 3 and 4 show that the mean difference is closer to 0 when our approach is used in both the Mexicans and Puerto Ricans. The 1KG-Chrom-based correlation estimates generated differences in true versus estimated that were the closest to zero amongst all approaches. We can see from Tables 3 and 4 that 1KG-Chrom has the smallest variance for the differences in true versus estimated joint statistics. The ‘best guess’ panels had the highest variance of all approaches except for 1KG-Genome in the Puerto Ricans. Additionally, we examined all estimated joint statistics that were more than 2 chi-squared units from the truth. In Mexicans, we saw 122 such statistics for the MXL and 22 for 1KG-Chrom (Fig. 3a). A similar trend is seen in Puerto Ricans as well, with 53 large deviations for the PUR and 3 for 1KG-Chrom (Fig. 3b). The decrease in frequency and magnitude of large differences demonstrates that using Adapt-Mix can help reduce the number of false positives in a joint analysis using reference panels. However, high deviations seen in both methods indicate that regardless of approach there is potential to misestimate the pairwise correlation coefficients of SNPs.

Fig. 3.

Histogram of the deviations from the true joint statistic when using a ‘best guess’ panel and Adapt-Mix to estimate Σ for joint-testing. (a) Joint testing for GALA II Mexicans. MXL deviations are shown in red and 1KG-Chrom is shown in blue. (b) Joint testing for GALA II Puerto Ricans. PUR deviations are shown in orange and 1KG-Chrom is shown in blue

3.2 Real data

3.2.1 Population Frequencies

We applied our method to the C4D coronary artery disease dataset from the CARDIoGRAMplusC4D consortium (CARDIoGRAMplusC4D, Coronary Artery Disease (C4D) Genetics Consortium, 2011; Schunkert et al.., 2011). In the C4D study, the discovery cohort consisted of 14 790 South Asians and 15 692 Europeans. South Asians are known to have undergone admixture between two ancestral populations, with one of the ancestral populations being genetically similar to Europeans (Moorjani et al., 2013; Reich et al., 2009). Consistent with the admixture seen in South Asians, we see mixture frequencies for C4D that are assigned primarily to the European and the South Asian panels (Fig. 1).

3.2.2 Imputation

The C4D data provided us with an opportunity to assess how our method affects the performance of z-score imputation in the context of a dataset with different population structure than that used in the simulations. Unlike our simulations, where everybody was admixed, the summary statistics in C4D were generated using a mixture of individuals with homogenous ancestries (Europeans) and heterogeneous ancestries (South Asians). As we did for the simulated data, we used MSE and r of the imputed z-scores as our performance metrics. Here, we estimated Σ using a ‘best guess’ reference panel, 1KG-Chrom and 1KG-Window. We chose to optimize frequencies for the 1KG reference panels over each chromosome and each window because these two approaches performed the best in our simulations. We imputed the 100th SNP in each window and we restricted our analyses here to SNPs that had (mixture) MAF $\ge 0.01$.

As the ‘best guess’ reference panel for C4D, we used GIH and CEU because the C4D discovery cohort was composed of roughly an equal number of individuals with a European or South Asian ancestry. When imputing we saw similar results to our simulations. Compared to using CEU or GIH, there was a decrease of 30.1% or 36% in MSE, respectively (Table 5). In terms of r, we saw increases of about 7% over CEU and about 9% over GIH for both 1KG-Window and 1KG-Chrom. The increase in correlation is equivalent to an increase of 15% in effective sample size compared to CEU.

Table 5.

The performance of each reference panel when imputing z-scores for the C4D dataset

Panel	n	MSE	r
CEU	2637	0.379	0.813
GIH	2627	0.414	0.796
1KG-Chrom	2651	0.272	0.870
1KG-Window	2628	0.265	0.872

4 Discussion

Summary statistics-based methods requiring an estimate of the genetic correlation matrix are becoming increasingly popular; however, very few GWAS include LD information in their released data. In prior work, this information has been approximated by using LD information from ‘best guess’ reference panels, but here we show that this can lead to high error rates even when a population closely matching the study population is available (Zaitlen et al.., 2009). Our method can be used to improve the accuracy of any summary statistics-based method that requires LD information by more accurately estimating the local genetic correlation structure using information available across several reference populations.

Our simulations have demonstrated the importance of accurately estimating the genetic correlation matrix. Using Adapt-Mix to estimate LD for summary statistics methods can increase their power and decrease their false positive rates. For example, for z-score imputation, Pasaniuc et al. (2014) showed that as long as there is a best guess reference panel available, there is no increase in false positive rate when imputing summary statistics. However, in the case that there is no best guess panel available, we have shown that there is a potential for increased false positives by using the wrong reference panel.

One of the biggest benefits of our method is allowing the analysis of arbitrary populations when a matching reference panel is not available. We were able impute z-scores and compute joint statistics with better precision ‘best guess’ panels alone even after leaving out the relevant ‘best guess’ panels from our computation of Σ. For datasets with admixed individuals, the high variability of ancestry proportions may make it harder to consistently model LD in an accurate manner with a single reference panel. For example, in the Native American component Latinos, there is a high level of population substructure (Wang et al.., 2008). In the 1000 Genomes reference panels, there are currently no Native American reference panels available. Although proxy populations such as CHB and JPT are often used, they are unlikely to capture the full resolution of each underlying sub-population. Accounting for all the fine scale differences seen in admixed individuals will improve with the collection of additional reference panels.

In this work, we aimed to minimize the MSE of imputed summary statistics in our objective function because imputation was one of our main focuses. For other purposes, it may be more appropriate to use a different objective depending on how the pairwise correlation estimates will ultimately be used. For example, Hormozdiari et al. (2014) use summary statistics to fine map causal variants by finding the set of variants that maximize the likelihood of a multivariate normal distribution. In this case, optimizing frequencies for reference panels by using the multivariate normal likelihood may improve performance.

Improvements to Adapt-Mix may be made by using an out-of-sample approach to learning the mixture frequencies due to the potential of overfitting. Typically, overfitting will cause high prediction error variances. We have shown though, with the example of joint-testing, that overfitting should not be a major concern as the error variances are smaller when using Adapt-Mix compared with a ‘best guess’ panel. Another enhancement could be made to Adapt-Mix by using partial correlations. Often covariates such as principal components are included in GWAS, which alter the genetic correlation structure of the individuals being studied. Partial correlations which account for these covariates may provide even more accurate estimates of the Σ for use in summary statistics methods.