INTRODUCTION
The ultimate teacher on human physiology is human pathology and the clinical trials aimed at its amelioration. However, the pathway between disease and cure most frequently arises from a reductionist approach. Perhaps no better illustration of this process is the history of the diagnosis and treatment of hemophilia A, which involved the identification of the defect in blood, in plasma, in cryoprecipitate [1] and ultimately by the absence or impairment of the factor (F)VIII molecule. Essential to the evolution of the development of knowledge and treatment were in vitro tests and experimental methods, the results of which could be validated in clinical trials while simultaneously providing the quantitative methods essential to identify the FVIII molecule.
The aPTT test [2], still essential in hemophilia diagnosis and management, is clearly biologically artificial, employing citrate plasma and a non-physiologic activator with excess phospholipid. Nonetheless, its utility is not in doubt. However, the relevance of some molecular defects in “hemostasis” identified using the aPTT are in doubt since they are not associated with a hemostatic pathology.
Our laboratory, while predominately reductionist in approach uses a variety of models including: numerical synthesis of the clotting reaction solved on a computer [3]; closed and open (flow) systems utilizing the reconstituted synthetic plasma clotting proteome [4-6]; minimally altered, corn trypsin inhibitor-treated whole blood with and without endothelial and inflammatory cells [7, 8]; and blood oozing from microvascular wounds in volunteers [9]. The numerical models have been used in studies to discriminate between potential mechanistic pathways [10-12], epidemiologic studies of hemorrhage control and thrombosis [13] and in support of drug design and evaluation[14] [15, 16].
NUMERICAL MODELS SYSTEMS AND THEIR VALIDATION
Human biology is fundamentally opaque while numerical models are fundamentally transparent (Figure 1); the gradient from numerical models through proteome to human physiology becomes less and less transparent. When the results of these models converge we believe we understand the process; when they diverge it becomes the basis of the discovery of new pathways. The fundamental utility of the role of numerical models in the long term project of understanding coagulation has and continues to be recognized by a number of investigators at all levels of empirical model complexity. Mathematical constructs of the coagulation reaction network have been developed using ensembles of differential equations [3, 17-22] or more elaborate constructs for both closed and flow based model systems [19, 23-32]. All these numerical models develop within and from the gradient of empirical model systems used to investigate the chemistry of coagulation. The coincidence of numerical and empirical proteome models suggests the models are correct at this level.
Figure 1.
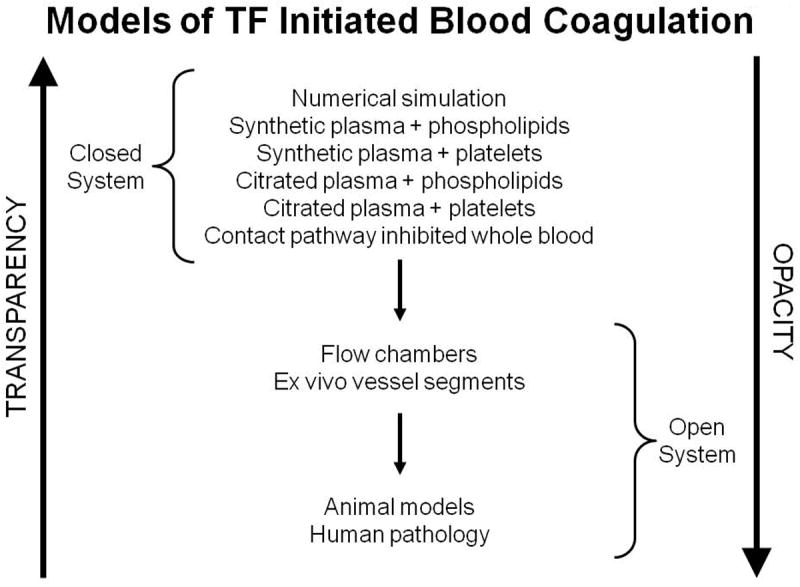
The gradients of biochemical “transparency” and biological “opacity” proceeding from numerical models to human biology [62]. This research was originally published in: Mann KG, Brummel-Ziedins K, Orfeo T, Butenas S. Models of blood coagulation. Blood Cells Mol Dis. 2006; 36: 108-17. With permission.
Numerical models present a distillation of the insights from empirical models and offer the promise of predicting outcomes when reaction networks are perturbed. Like the empirical models from which they derive their content, numerical models are both incomplete and imperfect representations of the living systems they attempt to describe. The gradient from totally transparent numerical models to human physiology (Figure 1) requires constant empirical validation with increasingly complex and opaque empirical studies. Any discontinuity observed in proceeding through the gradient results in the identification of new discoveries. At each step in the progression (Figure 1), the costs and time for execution increases in an exponential fashion. Numerical hypotheses tested on the computer take seconds and cost little. Clinical trials take years and are exorbitantly expensive.
(a)“Clot Speed”
Biochemistry is fundamentally a reductionist science. My laboratory’s initial foray into blood clotting dealt with the isolation and characterization of the multiple forms of thrombin [33] and the activation of prothrombin [34]. These studies subsequently proceeded through the isolation of FV [35], its activation to FVa [36], and the participation of FVa, FXa and phospholipid in the prothrombinase complex [37]. The greater than 300,000 fold increase in prothrombin activation rates by the FXa, FVa, phospholipid, Ca2+ complex (prothrombinase) when compared to FXa in solution led to the thesis that part of the amplification arose from compartmentalization of the reactants in a restricted volume element such that substrate (prothrombin) and enzyme (FXa-FVa) were simultaneously confined to a limited volume on the surface of a phospholipid vesicle [38] (Figure 2). The nominal concentrations of enzyme and substrate in bulk solution only predicts the “true” reaction conditions occurring in the restricted volume identified as the “interface shell” surrounding the lipid vesicle where enzyme and substrate must meet. As a consequence, the binding of substrate and enzyme were themselves in competition for phospholipid binding sites. Thus alterations of any component’s concentration would alter the phospholipid bound concentrations of the other components as they occupied similar sites.
Figure 2.
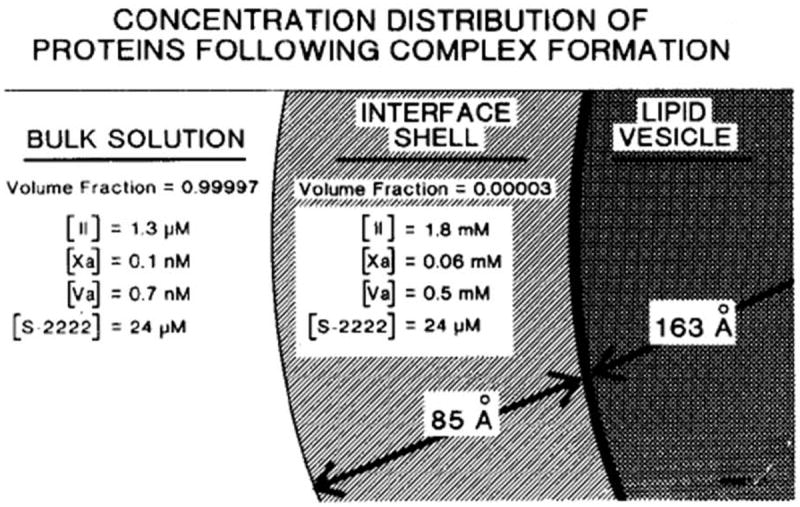
Model depicting distributions of prothrombin, FXa, and FVa between bulk solution and the phospholipid vesicle in the assembly of prothrombinase [38]. The region designated as interface shell is presumed that in which enzyme (FXa) and substrate concentrate, and in which catalysis occurs. The volume of this region is about 4.6 × 10-20 liters/vesicle. The indicated concentrations are those which apply at equilibrium and were calculated from the initial concentrations stated in the text and published binding parameters for the interactions of the various species with phospholipid vesicles and each other. The indicated distribution of components plus the enhanced Vmax conferred by FVa are sufficient to enhance the rate of prothrombin conversion (per unit volume of bulk solution) by a factor of 2.8 × 105. This research was originally published in J Biol Chem. Nesheim ME, Eid S, Mann KG. Assembly of the prothrombinase complex in the absence of prothrombin. J Biol Chem. 1981; 256: 9874-82. © The American Society for Biochemistry and Molecular Biology.
The classical approach in enzyme kinetics with multiple reactants involves altering one component while keeping the others constant. This is impossible with studies of prothrombinase because of the multiple equilibria which change occupancy in the hypothesized restricted volume.
Our approach to test the complex binding-restricted volume hypothesis was to develop a numerical simulation “clotspeed,” where the newly available Apple II computer was used to predict the consequences of alterations in the concentrations of the various components on the production of thrombin [39]. A week of desktop computer time produced hypothetical titrations of the various reactants over several orders of magnitude. These syntheses predicted conditions under which concentrations of substrate (fII), enzyme (FXa/FVa) and phospholipid (PS) would inhibit the reaction. In this paradoxical prediction, the addition of excess enzyme or excess substrate to the reaction would produce inhibition through site competition, while excess phospholipid would dilute the reactants. Figure 3 shows the predicted rate of thrombin production as the enzyme (fXa-fVa) concentration is increased with constant substrate (fII) and vesicle concentrations. Increased fXa-fVa occupancy results in decreased fII binding and ultimately a paradoxical decrease in rate of thrombin formation. Following several weeks of empirical enzymology studies based upon the predictions of the numerical model, we tested empirically the conditions under which enzyme, substrate and phospholipid would paradoxically inhibit the reaction and found the model to be correct.
Figure 3.
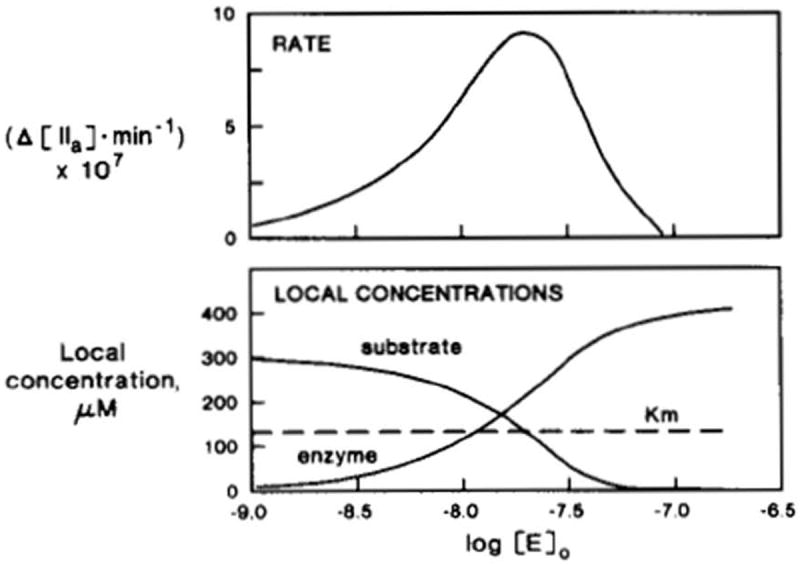
Simulated inhibition of initial rates of prothrombin activation by excess enzyme [39]. The logarithms of enzyme concentrations are indicated by the units of the horizontal axis. Top, simulated reaction rates (moles of thrombin*min-1) are shown; bottom, local (interface shell) concentrations are shown for both substrate and enzyme. With increased levels of added enzyme, its local concentration increases, resulting in increased reaction rates. Excess enzyme, however, competes with the substrate in the interface shell, lowering its local concentration, thus resulting in decreased reaction rates. This research was originally published in J Biol Chem. Nesheim ME, Tracy RP, Mann KG. “Clotspeed,” a mathematical simulation of the functional properties of prothrombinase. J Biol Chem. 1984; 259: 1447-53. © The American Society for Biochemistry and Molecular Biology.
(b) The plasma coagulation proteome
Over the next three decades a remarkable series of research contributions from many laboratories led to the isolation and characterization of the components of the plasma procoagulation pathway and their quantitative kinetics of formation and function [40]. We constructed the empirical plasma-tissue factor (TF) pathway procoagulant proteome utilizing isolated proteins [4]. We simultaneously modeled the reaction system using the required collection of ordinary differential equations [41]. Subsequently the stoichiometric inhibitors antithrombin and TF pathway inhibitor were added to the empirical and numerical models [3, 42]. New models currently developed but not yet published include the contributions of FXI [43], platelets, fibrinogen, protein C [44] and thrombomodulin. These models are always tested empirically prior to their publication [4] and subsequently [14, 15, 45, 46]. In addition, mathematical analyses probing the sensitivity of these models to variations in rate constants and coagulation factor composition have been performed [47, 48]. Without validation numerical models are of little use. Testing requires the empirical reconstitution of the appropriate proteome from molecular and cellular elements. Until empirically validated, a numerical model cannot be rationally applied and remains only a “flight of fancy”.
APPLICATIONS
1. Descriptions of molecular events
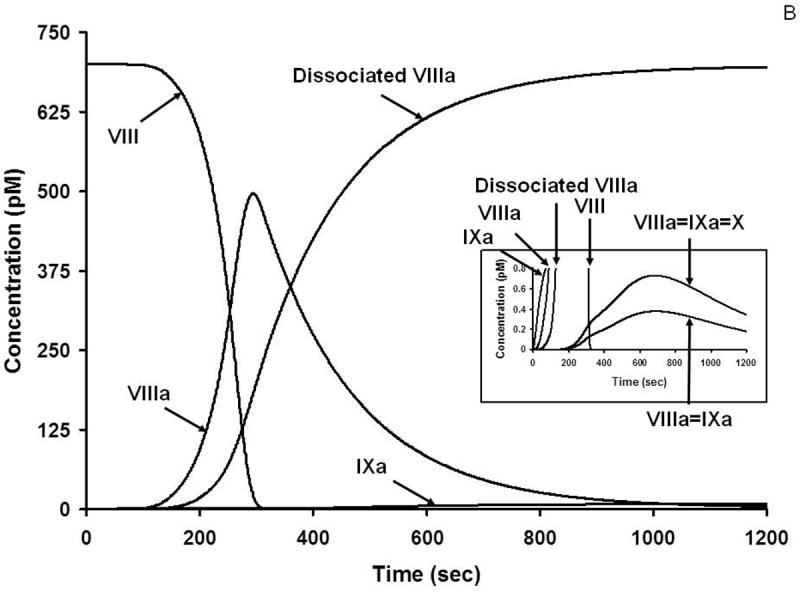
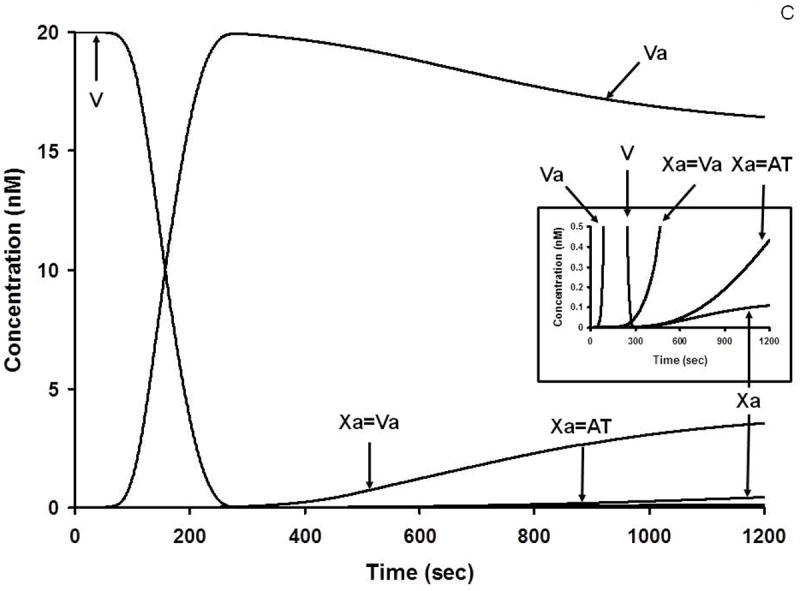
During the complex interplay of TF induced thrombin generation, multiple substrates are converted to products, products combine to form the procoagulant/complexes, stoichiometric inhibitors defeat the procoagulant enzymes and the dynamic thrombin-thrombomodulin-EPCR system inactivate FV/FVa and FVIlI/FVIIIa. Collectively the inhibitory systems terminate the reaction. Thus, as the reactions proceed, multiple substrates, products, enzyme complexes and inhibitor complexes are formed and consumed. The distribution and the concentrations of the initial substrates range from micromolar to nanomolar; thus the evolution of intermediates and products covers an extraordinary concentration range, most of which is not measurable by available analytical tools. Empirical quantitative methods are frequently inadequate to determine the time course of appearance and disappearance of many species. In contrast, the computer is not limited by these difficulties. Figure 4 illustrates the history of substrate-product relationships for the extrinsic FXase (Figure 4A) the intrinsic FXase (Figure 4B) and prothrombinase (Figure 4C) over the course of a hypothetical TF initiated reaction. In each of these figures the consumption of zymogens and procofactors with the evolution of enzymes and cofactors is illustrated along with the appearance of the procoagulant complexes of fVIIa-Tf, fIXa-fVIIIa and fXa-fVa.
Figure 4.
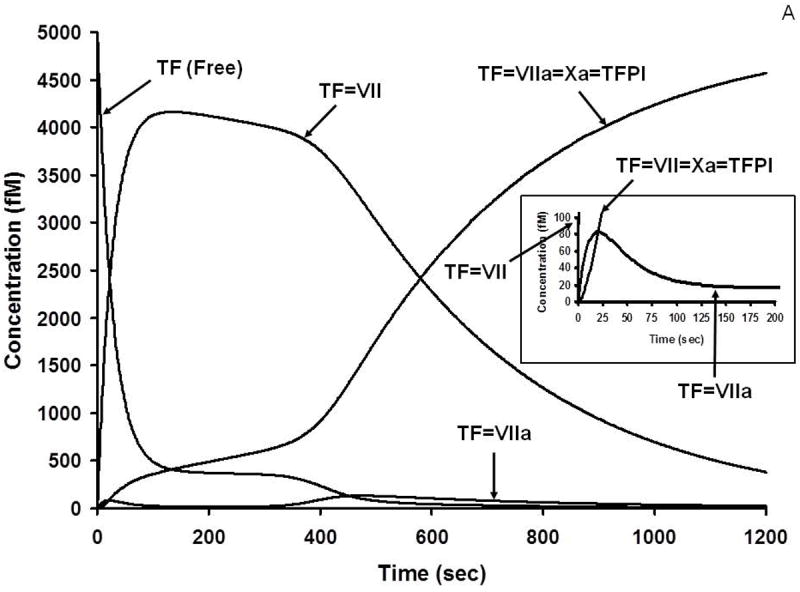
A. Numerical simulation: the formation of TF complexes during coagulation [10]. The reaction in electronic plasma is started by addition of 5 pM TF (t = 0). Data are expressed as metabolite concentration (femtomolar) versus time (s). Early formation of TF-FVIIa-FXa-TFPI complex is also shown (inset). This research was originally published in J Biol Chem. Orfeo T, Butenas S, Brummel-Ziedins KE, Mann KG. The tissue factor requirement in blood coagulation. J Biol Chem. 2005; 280: 42887-96. © The American Society for Biochemistry and Molecular Biology.
B. Numerical simulation: the formation of VIIIa complexes during coagulation. The reaction in electronic plasma is started by addition of 5 pM TF (t = 0). Data are expressed as metabolite concentration (picomolar) versus time (s). Complexes in the subpicomolar concentration range are also shown (inset). This research was originally published in J Biol Chem. Orfeo T, Butenas S, Brummel-Ziedins KE, Mann KG. The tissue factor requirement in blood coagulation.J Biol Chem. 2005; 280: 42887-96. © The American Society for Biochemistry and Molecular Biology.
C. Numerical simulation: the formation of Va and Xa complexes during coagulation. The reaction in electronic plasma is started by addition of 5 pM TF (t = 0). Data are expressed as metabolite concentration (nanomolar) versus time (s). Complexes in the subnanomolar concentration range are also shown (inset). This research was originally published in J Biol Chem. Orfeo T, Butenas S, Brummel-Ziedins KE, Mann KG. The tissue factor requirement in blood coagulation. J Biol Chem. 2005; 280: 42887-96. © The American Society for Biochemistry and Molecular Biology.
The expanded insets show the very low concentrations of these complexes actually presented. These latter relative concentrations are presented on an exponential scale in Figure 5. This figure illustrates the “amplifier” effect suggested by the Davie and Ratnoff “waterfall” [49] and by Macfarlane’s “cascade” [50].
Figure 5.
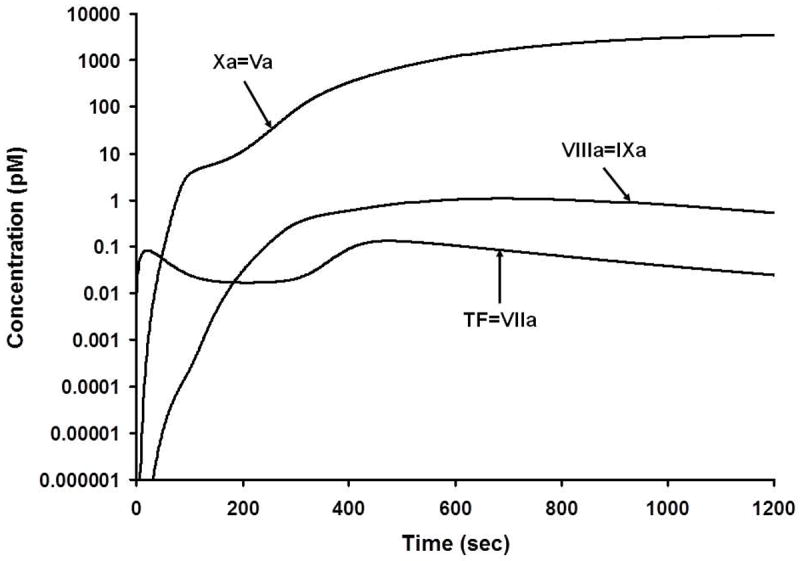
Numerical simulation of the active procoagulant complexes. The scale is logarithmic and illustrates the generation of these complexes from their onset at subfemtomolar levels. Mann, KG. Thrombin generation in hemorrhage control and vascular occlusion. Circulation. 124:225-35, 2011. PMID: 21747067
Figure 5 [51] highlights the relatively small concentrations of the active catalysts elaborated during the process. Each of these concentrations were calculated in seconds. While immeasurably small amounts of products and reactants are initially represented, they are consistent with measurements which can be made as higher product concentrations are evolved. Since only partial validation is possible, it must be anticipated that the lower concentrations of reactants depicted in these figures must have existed. This conclusion is not unlike the circumstance of viral infection prior to viral pathology or DNA amplification, i.e. there must have been exposure to immeasurable virus at the point of infection which could not have been directly quantitated. The absence of a requirement for TF over the course of the reaction and the stability of the procoagulant complexes once formed were predicted by these models and subsequently empirically validated [10, 52].
2. Drug Design
Multiple targets are potential choices for anticoagulant development. The qualities and effective concentrations of a potential drug are also questions, as the key to anticoagulation is to “thread the needle” of efficacy relative to safety. Early hypothetical studies evaluated different targets and the kinetic properties which would be required for drug efficacy. Analyses of on (kon) and off (koff) rates as well as overall affinity (Kd) were explored.
More recently, we have focused our analyses on new drug pharmacokinetics in human populations to estimate the safety and anticoagulant efficacy of the direct acting anticoagulants from dose to dose. These studies are then correlated with historical data associated with warfarin and heparin. These computational model studies have been validated by empirical proteome studies. Comparative evaluations of the new and historic anticoagulant performance using a validated computational version of the INR (cINR) attempts to predict drug efficacy and safety [15]. The hypothesis is that if we can mimic the function of the new drugs with respect to efficacious and safety ranges by comparison to the INR evaluated safe and therapeutic ranges we may be able to predict new drug “windows” of safety and efficacy on an individual recipient basis.
3. Epidemiology
The heterogeneity of the human blood coagulation phenotype is extremely broad in terms of “stimulus response” coupling [53]. The individual thrombin production response evaluated as the thrombin-antithrombin (TAT) accumulated with a fixed TF challenge is over five-fold in the blood of the healthy population (Figure 6). It seems reasonable to hypothesize that susceptibility to bleeding or thrombosis may in part be associated with the propensity to form thrombin. My colleagues have been collaborating with members of the epidemiology community to discern correlations between thrombin and FXa formation and hemostatic and thrombotic risk [46, 54]. These studies have also been extended to evaluate crisis events in arterial thrombosis [55]. The plasma factor composition data for the individuals in this study were utilized to predict the time courses for thrombin generation following a TF stimulus. These data show a propensity to generate more thrombin (based on the numerically modeled plasma) for the individuals during an acute coronary event when compared to the population of individuals with no event but equivalent atherosclerotic burden (Figure 7). These data suggest that the plasma composition of the affected subjects evoked more thrombin with the same TF stimulus.
Figure 6.
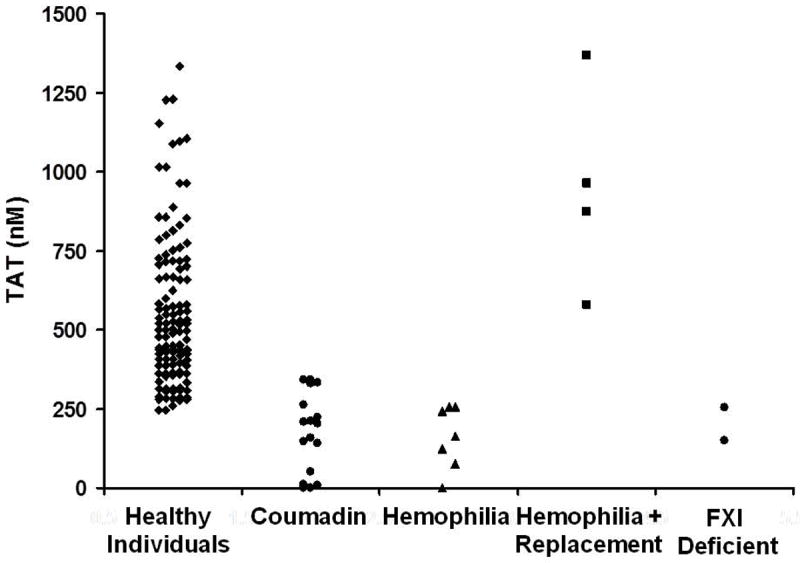
Thrombin–antithrombin (TAT) levels at 20 min as an evaluator of an individual’s hemostatic competence [53]. TAT at 20 min is illustrated for our group of 119 controls conducted over a 7-year time period, showing thrombin values ranging from approximately 250 to 1350 nM. Also represented are TAT data for individuals undergoing warfarin therapy, as well as individuals with hemophilia (with and without replacement) and FXI deficiency. Modified from: Brummel-Ziedins KE, Pouliot RL, Mann KG. Thrombin generation: phenotypic quantitation. J Thromb Haemost. 2004; 2: 281-8. With Permission.
Figure 7.
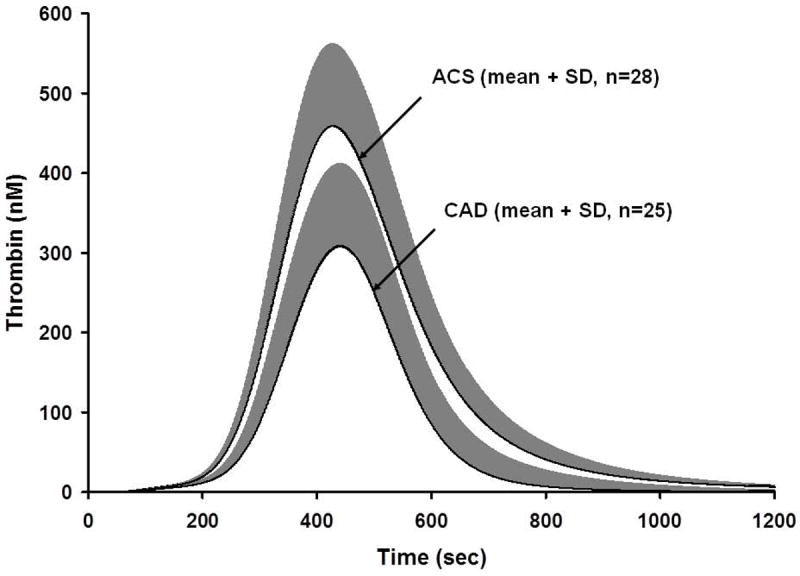
Thrombin simulations of acute coronary syndrome (ACS) and coronary artery disease (CAD) populations [55]. Plasma compositions from 28 ACS individuals and 25 CAD individuals were used to generate thrombin simulations over 1200 s. Data are shown as the mean for the ACS and CAD population. This research was originally published in: Brummel-Ziedins K, Undas A, Orfeo T, Gissel M, Butenas S, Zmudka K, Mann KG. Thrombin generation in acute coronary syndrome and stable coronary artery disease: dependence on plasma factor composition. J Thromb Haemost. 2008; 6: 104-10.
4. Real time coagulation process monitoring
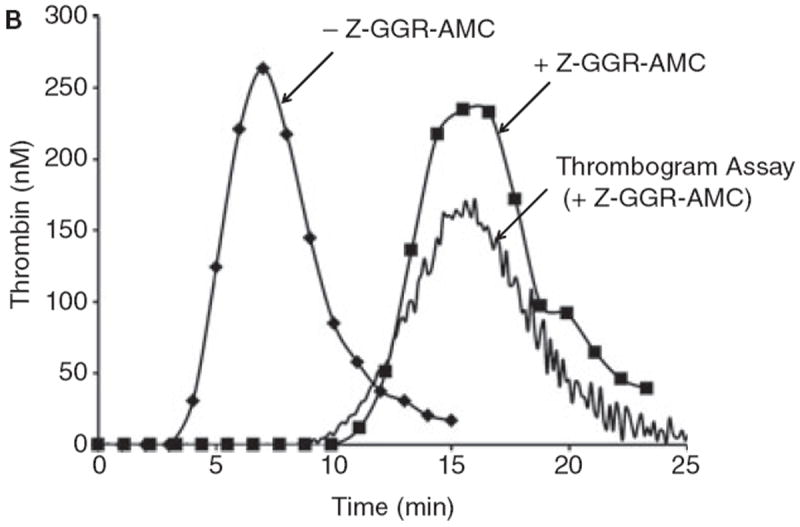
The incorporation of protease substrates into plasma to provide continuous evaluation of product formation has been utilized in biochemistry [38] and to evaluate human pathologic conditions [56]. This approach is valuable in that it provides substantially more information than a simple clot endpoint; which occurs with <5% of the thrombin generated [57]. However, the incorporation of a substrate for thrombin also provides additional complexity since the substrate is also an inhibitor and thus will influence the reaction progress [58]. The incorporation of Z-GGR-AMC to evaluate thrombin generation in the numerical model adds equations based on the Ki of the substrate toward various enzyme species including thrombin, fXa, fXa-fVa and fVIIa-Tf. The resulting numerical syntheses (± Z-GGR-AMC) presented in Figure 8A are compared to empirical equivalents constructed using the synthetic proteome (with subsampling), and a CAT assay monitoring, AMC (fluorescence) in Figure 8B.
Figure 8.
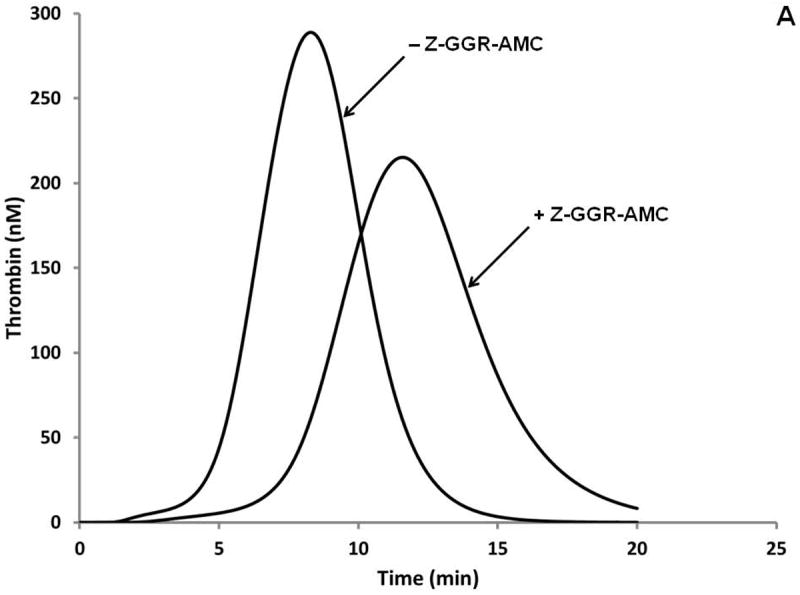
A. Simulations of the activation of the “normal” plasma proteome ± Z-GGR-AMC at 418 μM.
B. Synthetic proteome activation by 5 pM Tf with 50 μM phosphatidyl serine/phosphatidyl choline (25%:75%). Represented are the control with subsampling (no Z-GGR-AMC, diamonds); in the presence of 418 μM Z-GGR-AMC with subsampling (squares) and by continuous monitoring of Z-GGR-AMC hydrolysis (solid line). Note that the empirical curves with Z-GGR-AMC are right-shifted relative to the predictive curves of Figure 8A.
While the control proteome and model are nearly identical, the model does not replicate the proteome including Z-GGR-AMC whether evaluated by subsampling or continuous evaluation by hydrolysis of the internal substrate. These observations suggest that in addition to inhibiting thrombin, fVIIa-Tf, fXa and fXa-fVa, Z-GGR-AMC influences other reactions occurring during the Tf initiated reaction.
5. A Recent Exercise
Recently a colleague, Walter Dzik1, inquired whether the anticoagulant Pradaxa (dabigatran extilate) could be reversed by excess prothrombin. As an initial approach to this question we modeled active dabigatran at pharmacologic concentrations in a “normal” value plasma synthetic proteome with increasing prothrombin concentrations. The “plasma” dabigatran concentration chosen represents the Cmax, free concentration for a “normal” individual’s “plasma” [59, 60]. Shown in Figure 9 are the predicted thrombin generation results [56, 61] with and without dabigatran2 and additional prothrombin. As prothrombin concentrations are increased the area under the curve signifies more thrombin is produced. The data (Figure 9) suggest that an increase to 200% the prothrombin concentration would restore a reasonable propagation phase of thrombin generation while having a limited effect on the cINR (clot time). A corollary to this hypothesis is that a subject’s endogenous prothrombin concentration may alter the effectiveness of Pradaxa.
Figure 9.
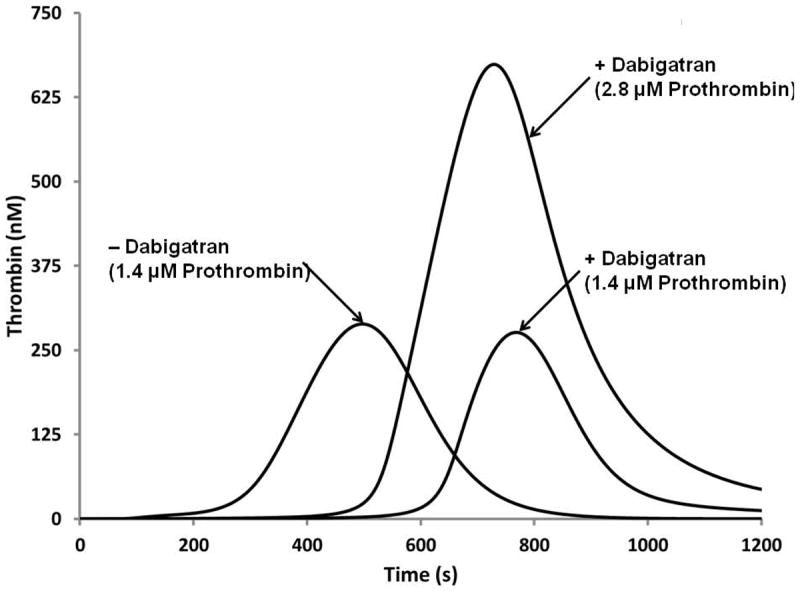
Numerical simulation of the reversal of dabigatran therapy with exogenous prothrombin. Dabigatran concentration (250 nM) is the effective Cmax concentration at the pharmacokinetic 50th percentile. Three curves are illustrated; a “normal” thrombin generation curve with 1.4 μM prothrombin, the same numerical proteome mixture with Dabigatran added and the latter to which a 100% increase in prothrombin is included.
Were we to pursue this question further, the next step would be to empirically reconstruct the synthetic empirical proteome in the presence of excess prothrombin and dabigatran (the active drug). Subsequently, we would test the hypothesis in corn trypsin inhibitor-blocked whole blood from volunteer donors to which dabigatran and excess prothrombin would be added in vitro. These studies, if successful, could initiate a clinical trial. At each step in the process there are exponential increases in time and cost. Thus the model is principally a “thinking” tool.
CONCLUSION
I enjoy the sport of fishing; the success of this venture is in part related to the number of times my bait is presented to a location where the fish are likely to reside, with bait that the fish might prefer to eat. The analogy with numerical models is that they efficiently and cheaply allow casting for the molecular and mechanistic “fish”. These models are not a panacea nor are they a replacement for empirical fishing, but they are a useful thinking tool.
Acknowledgments
This research was supported by the National Institutes of Health grant #P01HL46703 and the US Army Department of Defense contract #W911NF-10-1-0376. I would also like to acknowledge the contributions of my colleagues Dr. Kathleen Brummel-Ziedins, Dr. Saulius Butenas, Dr. Thomas Orfeo and Matthew Gissel in the preparation of this document.
Footnotes
Walter H. Dzik, MD, Blood Transfusion Service, Massachusetts General Hospital, Boston, MA.
Pradaxa is the prodrug of dabigatran.
CONFLICT OF INTEREST DISCLOSURE: Kenneth Mann is COB of Haematologic Technologies Inc.
References
- 1.Pool JG. Cryoprecipitated factor VIII concentrate. Thromb Diath Haemorrh Suppl. 1968;35:35–40. [PubMed] [Google Scholar]
- 2.Langdell RD, Wagner RH, Brinkhous KM. Effect of antihemophilic factor on one-stage clotting tests; a presumptive test for hemophilia and a simple one-stage antihemophilic factor assy procedure. J Lab Clin Med. 1953;41:637–47. [PubMed] [Google Scholar]
- 3.Hockin MF, Jones KC, Everse SJ, Mann KG. A model for the stoichiometric regulation of blood coagulation. J Biol Chem. 2002;277:18322–33. doi: 10.1074/jbc.M201173200. [DOI] [PubMed] [Google Scholar]
- 4.Lawson JH, Kalafatis M, Stram S, Mann KG. A model for the tissue factor pathway to thrombin. I. An empirical study. J Biol Chem. 1994;269:23357–66. [PubMed] [Google Scholar]
- 5.Haynes LM, Dubief YC, Orfeo T, Mann KG. Dilutional control of prothrombin activation at physiologically relevant shear rates. Biophys J. 2011;100(3):765–73. doi: 10.1016/j.bpj.2010.12.3720. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Haynes LM, Dubief YC, Mann KG. Membrane binding events in the initiation and propagation phases of tissue factor initiated zymogen activation under flow. J Biol Chem. 2012;287:5225–34. doi: 10.1074/jbc.M111.302075. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Rand MD, Lock JB, van’t Veer C, Gaffney DP, Mann KG. Blood clotting in minimally altered whole blood. Blood. 1996;88:3432–45. [PubMed] [Google Scholar]
- 8.Campbell JE, Brummel-Ziedins KE, Butenas S, Mann KG. Cellular regulation of blood coagulation: a model for venous stasis. Blood. 2010;116:6082–91. doi: 10.1182/blood-2010-01-266395. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Undas A, Brummel KE, Musial J, Mann KG, Szczeklik A. Simvastatin depresses blood clotting by inhibiting activation of prothrombin, factor V, and factor XIII and by enhancing factor Va inactivation. Circulation. 2001;103:2248–53. doi: 10.1161/01.cir.103.18.2248. [DOI] [PubMed] [Google Scholar]
- 10.Orfeo T, Butenas S, Brummel-Ziedins KE, Mann KG. The tissue factor requirement in blood coagulation. J Biol Chem. 2005;280:42887–96. doi: 10.1074/jbc.M505506200. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Butenas S, Orfeo T, Gissel MT, Brummel KE, Mann KG. The significance of circulating factor IXa in blood. J Biol Chem. 2004;279:22875–82. doi: 10.1074/jbc.M400531200. [DOI] [PubMed] [Google Scholar]
- 12.Orfeo T, Brufatto N, Nesheim ME, Xu H, Butenas S, Mann KG. The factor V activation paradox. J Biol Chem. 2004;279:19580–91. doi: 10.1074/jbc.M400727200. [DOI] [PubMed] [Google Scholar]
- 13.Brummel-Ziedins K, Vossen CY, Rosendaal FR, Umezaki K, Mann KG. The plasma hemostatic proteome: thrombin generation in healthy individuals. J Thromb Haemost. 2005:1472–81. doi: 10.1111/j.1538-7836.2005.01249.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Orfeo T, Butenas S, Brummel-Ziedins KE, Gissel M, Mann KG. Anticoagulation by factor Xa inhibitors. J Thromb Haemost. 2010;8:1745–1753. doi: 10.1111/j.1538-7836.2010.03917.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Orfeo T, Gissel M, Butenas S, Undas A, Brummel-Ziedins KE, Mann KG. Anticoagulants and the propagation phase of thrombin generation. PLoS One. 2011;6(11):e27852. doi: 10.1371/journal.pone.0027852. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Brummel Ziedins K, Rivard GE, Pouliot RL, Butenas S, Gissel M, Parhami-Seren B, et al. Factor VIIa replacement therapy in factor VII deficiency. J Thromb Haemost. 2004 Oct;2(10):1735–44. doi: 10.1111/j.1538-7836.2004.00922.x. [DOI] [PubMed] [Google Scholar]
- 17.Panteleev MA, Ovanesov MV, Kireev DA, Shibeko AM, Sinauridze EI, Ananyeva NM, et al. Spatial propagation and localization of blood coagulation are regulated by intrinsic and protein C pathways, respectively. Biophys J. 2006;90:1489–500. doi: 10.1529/biophysj.105.069062. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Luan D, Zai M, Varner JD. Computationally derived points of fragility of a human cascade are consistent with current therapeutic strategies. PLoS Comput Biol. 2007;3:e142. doi: 10.1371/journal.pcbi.0030142. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Anand M, Rajagopal K, Rajagopal KR. A model for the formation, growth, and lysis of clots in quiescent plasma. A comparison between the effects of antithrombin III deficiency and protein C deficiency. J Theor Biol. 2008;253:725–38. doi: 10.1016/j.jtbi.2008.04.015. [DOI] [PubMed] [Google Scholar]
- 20.Chatterjee MS, Denney WS, Jing H, Diamond SL. Systems biology of coagulation initiation: kinetics of thrombin generation in resting and activated human blood. PLoS Comput Biol. 2010;6 doi: 10.1371/journal.pcbi.1000950. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Mitrophanov AY, Reifman J. Kinetic modeling sheds light on the mode of action of recombinant factor VIIa on thrombin generation. Thromb Res. 2011;128:381–90. doi: 10.1016/j.thromres.2011.05.013. [DOI] [PubMed] [Google Scholar]
- 22.Lo K, Denney WS, Diamond SL. Stochastic modeling of blood coagulation initiation. Pathophysiol Haemost Thromb. 2005;34:80–90. doi: 10.1159/000089929. [DOI] [PubMed] [Google Scholar]
- 23.Hall CL, Slack SM, Turitto VT. A computational analysis of FXa generation by TF:FVIIa on the surface of rat vascular smooth muscle cells. Ann Biomed Eng. 1998;26:28–36. doi: 10.1114/1.120. [DOI] [PubMed] [Google Scholar]
- 24.Kuharsky AL, Fogelson AL. Surface-mediated control of blood coagulation: the role of binding site densities and platelet deposition. Biophys J. 2001;80:1050–74. doi: 10.1016/S0006-3495(01)76085-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Ataullakhanov FI, Panteleev MA. Mathematical modeling and computer simulation in blood coagulation. Pathophysiol Haemost Thromb. 2005;34:60–70. doi: 10.1159/000089927. [DOI] [PubMed] [Google Scholar]
- 26.Fogelson AL, Tania N. Coagulation under flow: the influence of flow-mediated transport on the initiation and inhibition of coagulation. Pathophysiol Haemost Thromb. 2005;34:91–108. doi: 10.1159/000089930. [DOI] [PubMed] [Google Scholar]
- 27.Xu Z, Chen N, Kamocka MM, Rosen ED, Alber M. A multiscale model of thrombus development. J R Soc Interface. 2008;5:705–22. doi: 10.1098/rsif.2007.1202. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Runyon MK, Kastrup CJ, Johnson-Kerner BL, Ha TG, Ismagilov RF. Effects of shear rate on propagation of blood clotting determined using microfluidics and numerical simulations. J Am Chem Soc. 2008;130:3458–64. doi: 10.1021/ja076301r. [DOI] [PubMed] [Google Scholar]
- 29.Wajima T, Isbister GK, Duffull SB. A comprehensive model for the humoral coagulation network in humans. Clin Pharmacol Ther. 2009;86:290–8. doi: 10.1038/clpt.2009.87. [DOI] [PubMed] [Google Scholar]
- 30.Xu Z, Kamocka M, Alber M, Rosen ED. Computational approaches to studying thrombus development. Arterioscler Thromb Vasc Biol. 2011;31:500–5. doi: 10.1161/ATVBAHA.110.213397. [DOI] [PubMed] [Google Scholar]
- 31.Fogelson AL, Hussain YH, Leiderman K. Blood Clot Formation under Flow: The Importance of Factor XI Depends Strongly on Platelet Count. Biophys J. 2012;102:10–8. doi: 10.1016/j.bpj.2011.10.048. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Xu Z, Lioi J, Mu J, Kamocka MM, Liu X, Chen DZ, et al. A multiscale model of venous thrombus formation with surface-mediated control of blood coagulation cascade. Biophys J. 2010;98:1723–32. doi: 10.1016/j.bpj.2009.12.4331. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Mann KG, Batt CW. The molecular weights of bovine thrombin and its primary autolysis products. J Biol Chem. 1969;244:6555–7. [PubMed] [Google Scholar]
- 34.Mann KG, Heldebrant CM, Fass DN. Multiple active forms of thrombin. II. Mechanism of production from prothrombin. J Biol Chem. 1971;246:6106–14. [PubMed] [Google Scholar]
- 35.Nesheim ME, Myrmel KH, Hibbard L, Mann KG. Isolation and characterization of single chain bovine factor V. J Biol Chem. 1979;254:508–17. [PubMed] [Google Scholar]
- 36.Nesheim ME, Mann KG. Thrombin-catalyzed activation of single chain bovine factor V. J Biol Chem. 1979;254:1326–34. [PubMed] [Google Scholar]
- 37.Nesheim ME, Kettner C, Shaw E, Mann KG. Cofactor dependence of factor Xa incorporation into the prothrombinase complex. J Biol Chem. 1981;256:6537–40. [PubMed] [Google Scholar]
- 38.Nesheim ME, Eid S, Mann KG. Assembly of the prothrombinase complex in the absence of prothrombin. J Biol Chem. 1981;256:9874–82. [PubMed] [Google Scholar]
- 39.Nesheim ME, Tracy RP, Mann KG. “Clotspeed,” a mathematical simulation of the functional properties of prothrombinase. J Biol Chem. 1984;259:1447–53. [PubMed] [Google Scholar]
- 40.Brummel-Ziedins KE, Orfeo T, Jenny NS, Everse SJ, Mann KG. Blood Coagulation and Fibrinolysis. In: Greer JP, Foerster J, Rodgers GM, Paraskevas F, Glader B, Arber DA, et al., editors. Wintrobe’s Clinical Hemotology. 12. New York: Lippincott Williams & Wilkins; 2009. pp. 528–619. [Google Scholar]
- 41.Jones KC, Mann KG. A model for the tissue factor pathway to thrombin. II. A mathematical simulation. J Biol Chem. 1994;269:23367–73. [PubMed] [Google Scholar]
- 42.van’t Veer C, Mann KG. Regulation of tissue factor initiated thrombin generation by the stoichiometric inhibitors tissue factor pathway inhibitor, antithrombin-III, and heparin cofactor-II. J Biol Chem. 1997;272:4367–77. doi: 10.1074/jbc.272.7.4367. [DOI] [PubMed] [Google Scholar]
- 43.Orfeo T, Gissel M, Whelihan MF, Butenas S, Mann KG. Factor XI activation in tissue factor-initiated blood coagulation. Blood. 2011;118:2239. [Google Scholar]
- 44.Bravo MC, Orfeo T, Mann KG, Everse SJ. Empirical validation of a mathematical model of the protein C pathway. J Thromb Haemost. 2011;9(Suppl. 2):357–8. [Google Scholar]
- 45.Butenas S, van’t Veer C, Mann KG. “Normal” thrombin generation. Blood. 1999;94:2169–78. [PubMed] [Google Scholar]
- 46.Brummel-Ziedins KE, Orfeo T, Gissel M, Mann KG, Rosendaal FR. Factor Xa generation by computational modeling: an additional discriminator to thrombin generation evaluation. PLoS One. 2012;7:e29178. doi: 10.1371/journal.pone.0029178. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Danforth CM, Orfeo T, Mann KG, Brummel-Ziedins KE, Everse SJ. The impact of uncertainty in a blood coagulation model. Math Med Biol. 2009;26:323–326. doi: 10.1093/imammb/dqp011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Danforth CM, Orfeo T, Everse SJ, Mann KG, Brummel-Ziedins KE. Defining the boundaries of normal thrombin generation: investigations into hemostasis. PLoS One. 2012;7:e30385. doi: 10.1371/journal.pone.0030385. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Davie EW, Ratnoff OD. Waterfall Sequence for Intrinsic Blood Clotting. Science. 1964;145:1310–2. doi: 10.1126/science.145.3638.1310. [DOI] [PubMed] [Google Scholar]
- 50.Macfarlane RG. An Enzyme Cascade in the Blood Clotting Mechanism, and Its Function as a Biochemical Amplifier. Nature. 1964;202:498–9. doi: 10.1038/202498a0. [DOI] [PubMed] [Google Scholar]
- 51.Mann KG. Thrombin generation in hemorrhage control and vascular occlusion. Circulation. 2011;124:225–35. doi: 10.1161/CIRCULATIONAHA.110.952648. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Orfeo T, Brummel-Ziedins KE, Gissel M, Butenas S, Mann KG. The nature of the stable blood clot procoagulant activities. J Biol Chem. 2008;283:9776–86. doi: 10.1074/jbc.M707435200. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Brummel-Ziedins KE, Pouliot RL, Mann KG. Thrombin generation: phenotypic quantitation. J Thromb Haemost. 2004;2:281–8. doi: 10.1046/j.1538-7933.2003.00576.x. [DOI] [PubMed] [Google Scholar]
- 54.Brummel-Ziedins KE, Orfeo T, Rosendaal FR, Undas A, Rivard GE, Butenas S, et al. Empirical and theoretical phenotypic discrimination. J Thromb Haemost. 2009;7(Suppl 1):181–6. doi: 10.1111/j.1538-7836.2009.03426.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Brummel-Ziedins K, Undas A, Orfeo T, Gissel M, Butenas S, Zmudka K, et al. Thrombin generation in acute coronary syndrome and stable coronary artery disease: dependence on plasma factor composition. J Thromb Haemost. 2008;6:104–10. doi: 10.1111/j.1538-7836.2007.02799.x. [DOI] [PubMed] [Google Scholar]
- 56.Hemker HC, Wielders S, Kessels H, Beguin S. Continuous registration of thrombin generation in plasma, its use for the determination of the thrombin potential. Thromb Haemost. 1993;70:617–24. [PubMed] [Google Scholar]
- 57.Brummel KE, Paradis SG, Butenas S, Mann KG. Thrombin functions during tissue factor-induced blood coagulation. Blood. 2002;100:148–52. doi: 10.1182/blood.v100.1.148. [DOI] [PubMed] [Google Scholar]
- 58.Butenas S, Mann KG. Caution in the interpretation of continuous thrombin generation assays. J Thromb Haemost. 2007;5:1084–5. doi: 10.1111/j.1538-7836.2007.02512.x. [DOI] [PubMed] [Google Scholar]
- 59.Blech S, Ebner T, Ludwig-Schwellinger E, Stangier J, Roth W. The metabolism and disposition of the oral direct thrombin inhibitor, dabigatran, in humans. Drug Metab Dispos. 2008;36:386–99. doi: 10.1124/dmd.107.019083. [DOI] [PubMed] [Google Scholar]
- 60.van Ryn J, Stangier J, Haertter S, Liesenfeld KH, Wienen W, Feuring M, et al. Dabigatran etexilate--a novel, reversible, oral direct thrombin inhibitor: interpretation of coagulation assays and reversal of anticoagulant activity. Thromb Haemost. 2010;103:1116–27. doi: 10.1160/TH09-11-0758. [DOI] [PubMed] [Google Scholar]
- 61.Mann KG, Whelihan MF, Butenas S, Orfeo T. Citrate anticoagulation and the dynamics of thrombin generation. J Thromb Haemost. 2007;5:2055–61. doi: 10.1111/j.1538-7836.2007.02710.x. [DOI] [PubMed] [Google Scholar]
- 62.Mann KG, Brummel-Ziedins K, Orfeo T, Butenas S. Models of blood coagulation. Blood Cells Mol Dis. 2006;36:108–17. doi: 10.1016/j.bcmd.2005.12.034. [DOI] [PubMed] [Google Scholar]


