Skip to main content
PMC home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2016 Sep 1.
Published in final edited form as: Neuroimage. 2015 Jun 11;118:667–675. doi: 10.1016/j.neuroimage.2015.06.016

Human brain diffusion tensor imaging at submillimeter isotropic resolution on a 3 Tesla clinical MRI scanner

Hing-Chiu Chang 1, Mark Sundman 1, Laurent Petit 2, Shayan Guhaniyogi 1, Mei-Lan Chu 1, Christopher Petty 1, Allen W Song 1, Nan-kuei Chen 1,*
PMCID: PMC4554968  NIHMSID: NIHMS699628  PMID: 26072250

Abstract

The advantages of high-resolution diffusion tensor imaging (DTI) have been demonstrated in a recent post-mortem human brain study (Miller et al., NeuroImage 2011;57(1):167–181), showing that white matter fiber tracts can be much more accurately detected in data at submillimeter isotropic resolution. To our knowledge, in vivo human brain DTI at submillimeter isotropic resolution has not been routinely achieved yet because of the difficulty in simultaneously achieving high resolution and high signal-to-noise ratio (SNR) in DTI scans. Here we report a 3D multi-slab interleaved EPI acquisition integrated with multiplexed sensitivity encoded (MUSE) reconstruction, to achieve high-quality, high-SNR and submillimeter isotropic resolution (0.85 × 0.85 × 0.85 mm3) in vivo human brain DTI on a 3 Tesla clinical MRI scanner. In agreement with the previously reported post-mortem human brain DTI study, our in vivo data show that the structural connectivity networks of human brains can be mapped more accurately and completely with high-resolution DTI as compared with conventional DTI (e.g., 2 × 2 × 2 mm3).

Introduction

The advantages of high-resolution diffusion tensor imaging have been clearly demonstrated in a recent imaging study, which achieved 0.73 × 0.73 × 0.73 mm3 resolution at 3 Tesla, of post-mortem human brain (Miller et al., 2011). This study shows that white matter fiber tracts, including curved and crossing pathways, can be much more accurately detected in data at submillimeter isotropic resolution, as compared with conventional DTI data (e.g., 2 × 2 × 2 mm3) (Miller et al., 2011).

In addition to post-mortem human brain imaging, in vivo human brain DTI at high in-plane resolution (e.g., 0.5 × 0.5 × 6 mm3) has also been achieved in studies using a number of 2D acquisitions, including interleaved echo-planar imaging (EPI) (Bammer, 2003; Chen et al., 2013; Jeong et al., 2013; Miller and Pauly, 2003; Van et al., 2009), interleaved spiral imaging (Butts et al., 1997; Li et al., 2005; Liu et al., 2004; Truong and Guidon, 2013), readout segmented EPI (Porter and Heidemann, 2009), short-axis PROPELLER EPI (Skare et al., 2006), and PROPELLER fast spin-echo pulse sequences (Pipe et al., 2002). However, because of the limited signal-to-noise ratio (SNR) and difficulty in effectively suppressing fat signals for thin slices (e.g., < 1.5 mm), it is challenging to achieve submillimeter isotropic resolution with 2D DTI protocols. These limitations have been partially addressed in a recently developed 3D multi-slab parallel EPI based DTI technique, making it possible to acquire human brain DTI data at 1.3 × 1.3 × 1.3 mm3 resolution (Engstrom and Skare, 2013). However, due to the undesirable noise amplification associated with parallel EPI reconstruction, it remains challenging to simultaneously achieve both high SNR and high resolution using existing 3D parallel EPI based DTI protocols. To our knowledge, in vivo human brain DTI at submillimeter isotropic resolution has not yet been routinely achieved.

In this paper we report that, through integrating 3D multi-slab interleaved EPI acquisition and multiplexed sensitivity encoded (MUSE) reconstruction (Chen et al., 2013), in vivo human brain DTI of high quality, high SNR and submillimeter isotropic resolution (specifically: 0.85 × 0.85 × 0.85 mm3) can be achieved on a 3 Tesla clinical MRI scanner. We show by several examples that the structural connectivity networks of human brains can be mapped more accurately and completely with high-resolution DTI as compared with conventional DTI (e.g., 2 × 2 × 2 mm3).

Methods

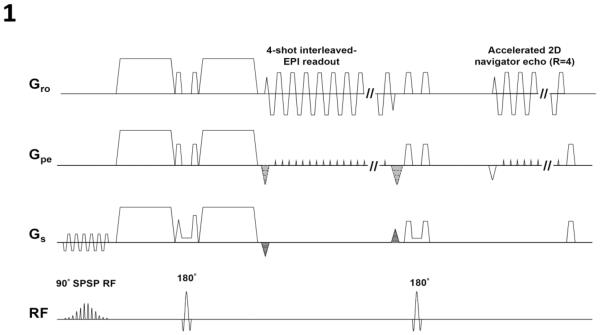
Figure 1 shows slab-selected 3D interleaved EPI sequence that we used to acquire diffusion-weighted signals (after the first 180° pulse) and 4× accelerated navigator echoes (after the second 180° pulse: without kz encoding). It has been shown previously that this DWI sequence, with phase-encoding gradients applied along the slice-direction for 3D encoding, has higher SNR efficiency than 2D DWI and is well suitable for high-resolution imaging (Engstrom et al., 2014; Engstrom and Skare, 2013; Frank et al., 2010; Frost et al., 2014; Frost et al., 2013; Van et al., 2014).

Figure 1.

Figure 1

Open in a new tab

A slab-selected 3D interleaved EPI pulse sequence that acquires diffusion weighted signals and accelerated navigator signals.

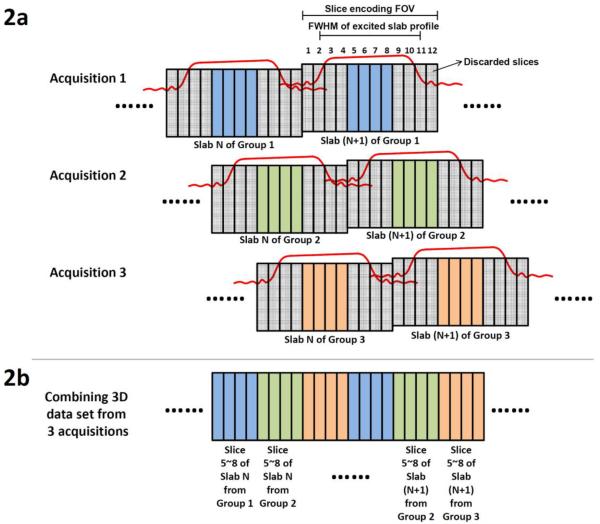
A well-known challenge in a slab-selected 3D DWI scan is that the signals along the slice-direction may be nonuniformly distorted when the RF excitation pulses are not well calibrated. In our experiments, we simply used an existing spatially-spectrally selective RF pulse that was designed for 2D EPI (i.e., a GE product) in our slab-selected 3D DWI scans without implementing an RF pulse suitable for 3D imaging. For this reason, we needed to 1) discard two thirds of the acquired slab signals (where RF profile distortions were pronounced: Figure 2a), and 2) repeat the scans three times to acquire whole-brain images without any gap (Figure 2b).

Figure 2.

Figure 2

Open in a new tab

(a) Three sets of 3D images (with slab profiles shifted) are acquired. (b) The acquired data are combined to produce a final set of 3D images with minimal through-plane signal non-uniformity resulting from RF profile distortions.

DTI data were acquired from four healthy volunteers on a 3 Tesla MRI scanner (MR750, General Electric, Waukesha, WI, USA) equipped with an 8-channel head coil. Scan parameters of our slab-selected 3D 4-shot interleaved EPI pulse sequence included: effective TEs = 59 ms (for image signals) and 115 ms (for navigator echoes), TR = 3000 ms, partial-Fourier factors along the ky direction = 70% (for image signals) and 67% (for navigator echoes), slab thickness = 9.4 mm, FOVz = 10.2 mm, number of kz phase-encoding steps = 12, number of axial slabs = 39, FOVxy = 21.8 cm, matrix size = 256 × 256 × 12 per slab, voxel size = 0.85 × 0.85 × 0.85 mm3, number of diffusion encoding directions = 12 (for subject #1) or 6 (for subjects #2, #3 and #4), and b = 800 s/mm2. The scan time was 32 min for each acquisition. We acquired three sets of data (with slab profiles shifted: as illustrated with Figure 2) from subject #1, and thus the total imaging time was 96 min in a single scan session. Using the scheme shown in Figure 2b, the effective brain coverage along the z direction was 132.6 mm (156 slices) for subject #1. For subjects #2, #3 and #4, we acquired only a single data set (i.e., blue slices in Figure 2b), mainly to compare the SNR in images obtained from different reconstruction methods.

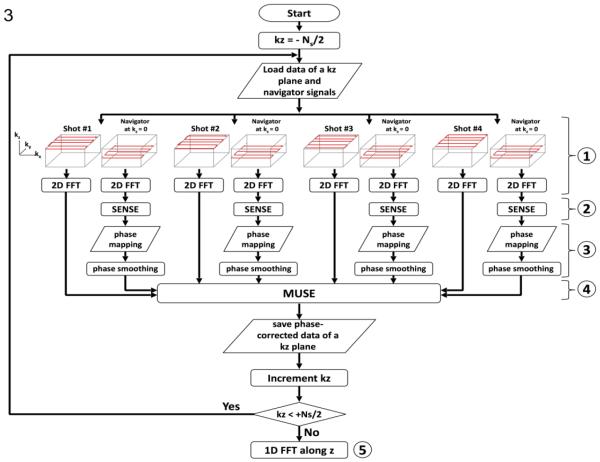
Shot-to-shot phase inconsistencies were measured from accelerated navigator echoes. This information was then used to minimize aliasing artifacts in interleaved EPI data through the MUSE algorithm (Chen et al., 2013), comprising five steps as shown in Figure 3: First, each 3D k-space interleaf and its associated accelerated 2D navigator echo were Fourier transformed along the kx and ky directions (i.e., into x-y-kz space); Second, images free from aliasing artifacts were reconstructed from accelerated navigator signals using the SENSE algorithm (Pruessmann et al., 1999); Third, the phase information obtained from step 2 was spatially smoothed; Fourth, the smoothed phase information (from step 3) and known coil sensitivity profiles were incorporated into a mathematical framework that jointly calculates the unknown source signals from all EPI segments in the x-y-kz space, producing slab-selected data free from aliasing artifacts. Fifth, the slab-selected data obtained from step 4 (in x-y-kz-space) were Fourier transformed along the kz direction, producing 3D images (in x-y-z-space). We then used the scheme shown in Figure 2b to combine signals from three acquisitions, producing a final set of 3D image data (with 156 slices). Afterward, the eddy current and motion correction was performed using the DTIPrep software (http://www.nitrc.org/projects/dtiprep/), and fractional anisotropy (FA) maps were calculated with the FSL software. A deterministic streamline tracking procedure was carried out using TrackVis (http://www.trackvis.org). A maximum curvature was set at 35°/voxel as the only tracking criterion, without applying other threshold or filter.

Figure 3.

Figure 3

Open in a new tab

The flow chart of reconstructing 3D interleaved DW-EPI data with 3D MUSE algorithm.

In addition to the MUSE reconstruction, we also processed the same k-space data with the conventional parallel MRI reconstruction algorithm to produce another set of 3D images for comparison. Specifically, step 4 of the above-described procedure was replaced by the conventional parallel imaging reconstruction, and images reconstructed from each of the EPI segments (in x-y-z plane) with the SENSE algorithm were phase corrected (using the smoothed phase variation maps obtain from step 3 described in the previous paragraph) and averaged in the complex domain. Similar to the MUSE-produced images, the eddy current and motion correction was performed with DTIPrep and FA maps were calculated with FSL.

To assess the dependence of the DTI quality on spatial resolution, a set of lower resolution images (2 × 2 × 2 mm3) was generated by down-sampling the MUSE-produced high-resolution images with a cubic resampling algorithm available from the FreeSurfer software package (https://surfer.nmr.mgh.harvard.edu/).

Results

Figure 4a shows x-y-kz space data of a selected slab, before applying the MUSE based artifact correction procedure. It can be seen that the uncorrected data were degraded by significant aliasing artifacts resulting from shot-to-shot phase variations (e.g., indicated by yellow arrows). Figure 4b shows that, after applying the 3D MUSE algorithm, the aliasing artifacts in each x-y-kz plane can be effectively removed. 3D images (in x-y-z space) before and after MUSE based artifact correction are shown in Figures 4c and 4d, respectively.

Figure 4.

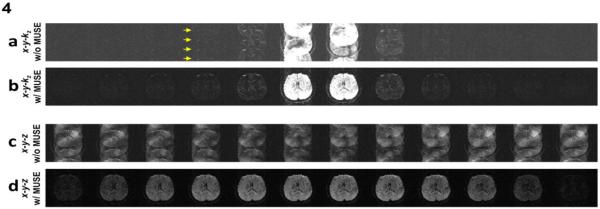
Figure 4

Open in a new tab

(a) 3D data (in x-y-kz space) of a selected slab are affected by aliasing artifacts due to shot-to-shot phase variations. (b) The aliasing artifact in each kz plane can be effectively removed with the 3D MUSE algorithm. (c) 3D images (in x-y-z space) without applying MUSE-based artifact correction procedure. (d) 3D images (in x-y-z space) reconstructed with the 3D MUSE algorithm.

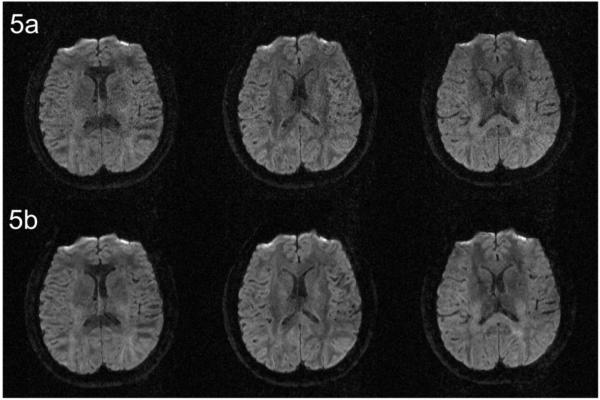
Figures 5a and 5b compare three selected DWI images (of an axial slice) reconstructed by the SENSE method and our 3D MUSE algorithm, respectively. It can be seen that the undesirable noise amplification associated with the conventional SENSE method can be largely avoided in 3D MUSE produced images. The white-matter SNR (measured by the ratio of “mean of signals” to “standard deviation of noises” within white matter ROIs across four subjects) of 3D MUSE produced images is 45%±7% higher than that of SENSE produced images (see Appendix).

Figure 5.

Figure 5

Open in a new tab

(a) Three selected DWI images (of an axial slice) reconstructed by the conventional SENSE algorithm. (b) DWI reconstructed by the developed 3D MUSE algorithm. This comparison shows that the undesirable noise amplification associated with the conventional SENSE method (the top row) can be largely avoided in 3D MUSE produced images (the bottom row).

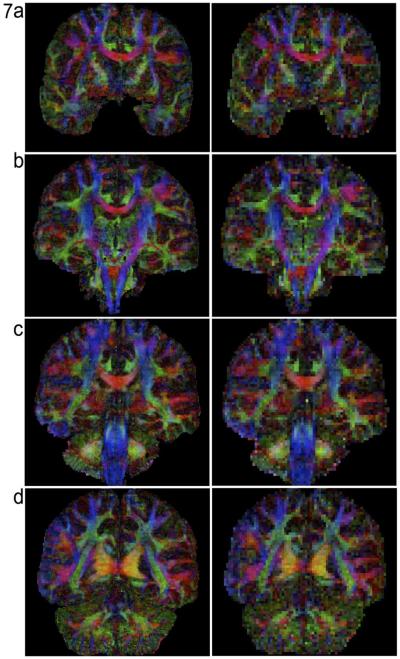
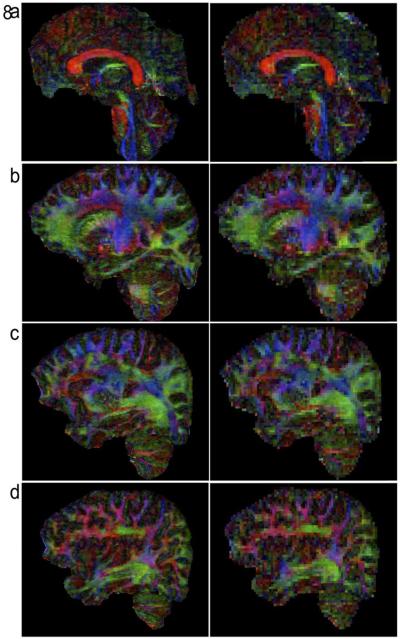
Figures 6, 7, and 8 compare FA maps of high-resolution (left column: 0.85 × 0.85 × 0.85 mm3) and conventional resolution (right column: 2 × 2 × 2 mm3) in axial, coronal and sagittal planes, respectively. It can be seen that, in agreement with the previously reported post-mortem imaging study, white matter fiber tracts can be better detected in high-resolution data. For example, the external and extreme capsules (arrows in Figure 6b) can only be resolved in FA maps of submillimeter resolution, but not in low-resolution FA maps.

Figure 6.

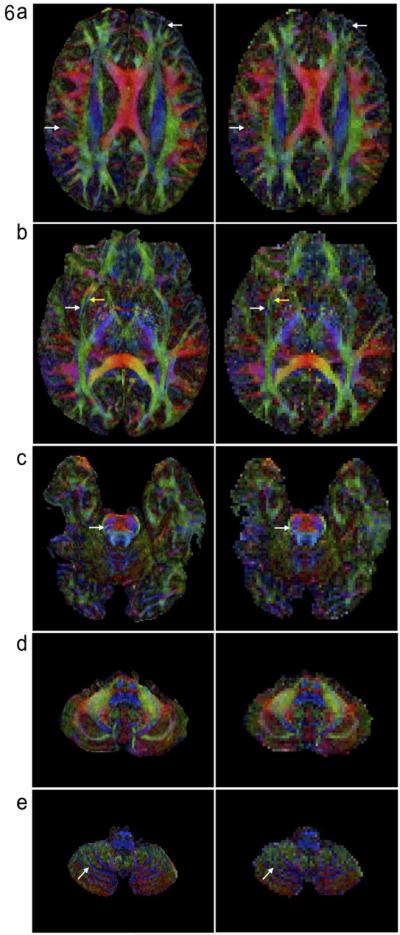
Figure 6

Open in a new tab

Comparison of high-resolution FA maps (left column: 0.85 × 0.85 × 0.85 mm3) and low-resolution FA maps (right column: 2 × 2 × 2 mm3) in axial-plane. The external and extreme capsules (arrows in Figure 6b) can only be resolved in FA maps of submillimeter resolution.

Figure 7.

Figure 7

Open in a new tab

Comparison of high-resolution FA maps (left column: 0.85 × 0.85 × 0.85 mm3) and low-resolution FA maps (right column: 2 × 2 × 2 mm3) in coronal-plane.

Figure 8.

Figure 8

Open in a new tab

Comparison of high-resolution FA maps (left column: 0.85 × 0.85 × 0.85 mm3) and low-resolution FA maps (right column: 2 × 2 × 2 mm3) in sagittal plane.

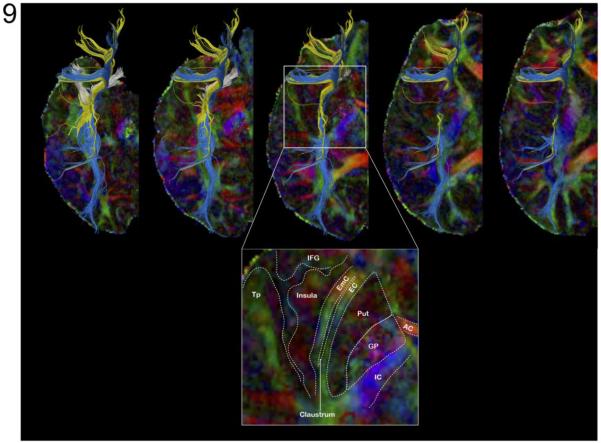
Figure 9 shows the fiber tracts of the inferior fronto-occipital fasciculus (IFOF) passing through the external (blue) and extreme (yellow) capsules and the fiber tracts of the uncinate fasciculus (white) using ROI seeds manually chosen from FA maps. These results confirm that spatially adjacent fiber tracts within IFOF, which may not be resolved with conventional DTI protocol, can be more accurately mapped with our high-resolution DTI protocol.

Figure 9.

Figure 9

Open in a new tab

Top: Fiber tracts of the inferior fronto-occipital fasciculus passing through the external (blue) and extreme (yellow) capsules and fiber tracts of the uncinate fasciculus (white) mapped with high-resolution FA map. Bottom: zoom on the external/extreme capsules for anatomical labeling. AC: Anterior Commissure; EC: External Capsule; EmC: Extreme Capsule; GP: Globus Pallidus; IC: Internal Capsule; IFG: Inferior Frontal Gyrus; Put: Putamen; Tp: Temporal pole.

Discussion

Our study shows that in vivo human brain DTI data of high quality and submillimeter resolution can be achieved with a protocol that integrates slab-selected 3D interleaved EPI acquisition and 3D-MUSE reconstruction. We have previously demonstrated that the MUSE reconstruction algorithm has better matrix inversion conditioning and is less susceptible to undesirable noise amplification, as compared with the SENSE reconstruction. As a result, in comparison to the slab-selected 3D parallel EPI data acquired with the same scan time, DWI images produced by our acquisition and reconstruction approaches have higher SNR in white-matter areas (by 45%±7%: see Appendix).

As shown in recent papers, 2D MUSE was designed to estimate shot-to-shot phase variations directly from interleaved EPI data without relying on navigator echoes (Chang et al., 2014; Chen et al., 2013; Chu et al., 2014). However, for 3D interleaved EPI, navigator signals with zero kz encoding are needed (Figure 1), because the shot-to-shot phase variations cannot be inherently estimated from weak DWI signals at high kz planes. We would like to point out that, unlike most interleaved EPI studies that acquired non-accelerated navigator echoes, in this study we implemented accelerated navigator acquisition so that high-resolution navigator echoes can be acquired at shorter TE. Another advantage of accelerated navigator scan, as compared with non-accelerated navigator scans, is that the associated EPI geometric distortions are more similar to that in interleaved EPI based DWI data, making the phase correction more reliable.

A limitation of our implemented 2D phase correction procedure is that it cannot correct through-slab phase variations, which fortunately can be reduced by choosing a thinner slab thickness. Previous studies have shown that the slab thickness should be smaller than 30mm in DWI scans with 1000 s/mm2 b-value (Engstrom et al., 2014; Engstrom and Skare, 2013; Frost et al., 2013; Van et al., 2014), otherwise the artifacts resulting from through-slab phase variations may not be well suppressed by 2D phase correction. In our study, the slab thickness was set to only 9.4 mm in DWI scans with 800 s/mm2 b-value, and therefore the through-slab phase variations were insignificant. We would like to point out that the slab thickness may need to be further reduced in DWI scans with higher b values (e.g., >1000 s/mm2).

In this study we simply used a product RF pulse, originally designed for 2D EPI, in our 3D DWI scans. As a result, we needed to repeat the scans three times (as illustrated in Figure 2) to acquire whole-brain DWI data without significant through-plane signal non-uniformity. Although this approach is obviously not ideal, we were able to demonstrate, as a proof of concept, the feasibility of acquiring DTI data at submillimeter resolution on a clinical scanner. In order to acquire whole-brain high-resolution DTI data within a more acceptable scan time (e.g., < 30 min), one has to use an appropriate 3D imaging RF pulse (Engstrom et al., 2014; Engstrom and Skare, 2013; Frank et al., 2010; Frost et al., 2014; Frost et al., 2013; Van et al., 2014) or incorporate the recently developed approaches that minimize the through-plane banding artifacts in 3D DTI scans (Van et al., 2014). In addition, the 3D DTI scan time can be reduced by incorporating partial Fourier scans along the kz direction (e.g., acquiring only 7 out of the 12 kz planes), although at the cost of SNR.

In this study, high-resolution DTI data were acquired from cooperative subjects who were able to stay still during scans, and thus we did not have to perform motion correction between the various interleaved shots for each imaging volume. If there is significant subject motion between EPI shots, either a prospective motion correction (Herbst et al., 2014) or a modified MUSE reconstruction procedure (Guhaniyogi et al., 2015) may be used to minimize artifacts resulting from shot-to-shot position changes.

Figures 6 to 8 clearly show that white matter fiber tracts can be much better visualized in high-resolution FA maps, as compared with low-resolution FA maps. Although in some cases the fiber tracking is more accurate in high-resolution DTI data (e.g., in Figure 8 and in (Song et al., 2014)), we would like to point out that the accuracy of fiber tracking depends on many other factors (such as the tracking algorithm; stopping criteria) and the advantages of the enhanced spatial-resolution for fiber tracking remain to be investigated.

As compared with single-shot EPI, interleaved EPI is less susceptible to geometric distortions resulting from eddy currents and susceptibility field gradients, and thus can produce high-resolution DWI data with higher spatial accuracy. We would like to point out that residual geometric distortions in interleaved EPI based DWI data may be further reduced with existing distortion correction techniques (Jezzard et al., 1998; Truong et al., 2011).

In conclusion, here we first demonstrate in vivo whole-brain DTI at submillimeter isotropic resolution on a clinical MRI scanner. The integration of slab-selected 3D interleaved EPI acquisition and 3D MUSE reconstruction makes it possible to simultaneously achieve high-quality, high-SNR and high-resolution DTI. With further protocol optimization (e.g., improved RF pulse design), the high-resolution DTI protocols should prove highly valuable for neuroscience research.

Acknowledgments

This research was supported by NIH grants R01 NS-074045, R21 EB-018419, R01 NS-075017, and R24 MH-106048.

Appendix: The SNR penalty in SENSE and MUSE reconstruction

As reported by Pruessmann et al., the noise amplification associated with the SENSE reconstruction can be quantified with a geometry-factor (g-factor) map, which mainly depends on coil sensitivity profiles (Pruessmann et al., 1999). Figures A1a to A1d show the 1/(g-factor) maps of SENSE reconstruction corresponding to four different acceleration factors (R=4, 2, 1.33 and 1) for the coil used in our study. The map shown in Figure A1d is also the 1/(g-factor) map of MUSE in the absence of shot-to-shot phase variation, which reconstructs images from full k-space data.

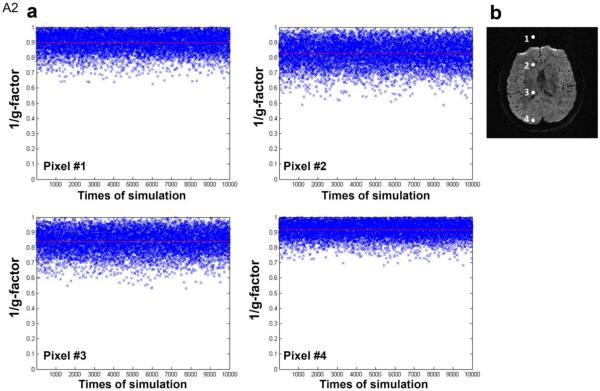
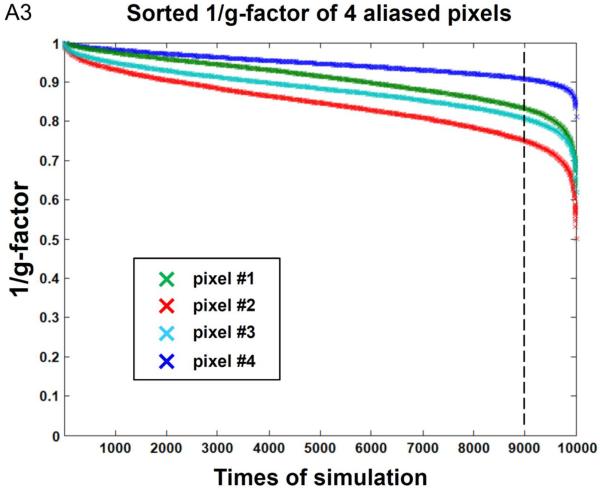
In order to investigate the impact of shot-to-shot phase variations on MUSE reconstruction of 4-shot DWI data, we first performed Monte Carlo simulation to measure g-factor with these inputs: 1) experimentally measured coil sensitivity profiles (derived from human data of subject #1) and 2) mathematically added phase variations (randomly distributed between +π and −π) across 4 shots. Figure A2a shows the Monte Carlo simulation results of 1/(g-factor) for MUSE produced signals in four aliased pixels (Figure A2b) corresponding to 10,000 sets of random phase variations. The means of 1/(g-factor) for four aliased pixels are greater than 0.8 (as indicated by red horizontal lines). Figure A3 shows the sorted 1/(g-factor) values, from high to low, for those 4 pixels shown in Figure A2. It can be seen (as indicated by vertical dotted lines) that 90% of the 1/(g-factor) values are greater than 0.83, 0.75, 0.81, and 0.91 for pixel #1, #2, #3, and #4, respectively. Our simulations shows that, although the SNR penalty in MUSE reconstruction depends on shot-to-shot phase variations, it is overall much less significant than that of 4x SENSE reconstruction (with 1/(g-factor) being 0.50, 0.35, 0.45, and 0.64 for those 4 chosen pixels).

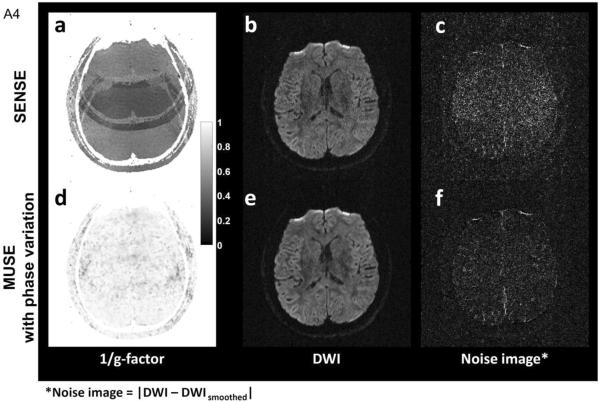
In addition to Monte Carlo simulation, we have also compared the noise levels in SENSE and MUSE images obtained from human scans. Figure A4a shows the 1/(g-factor) map for SENSE reconstruction with an acceleration factor of 4, based on coil sensitivity maps derived from data of subject #1. Figure A4b shows the DWI image obtained from averaging four SENSE produced images (i.e., reconstructed from each of the four EPI segments using SENSE algorithm), and Figure A4c shows the corresponding noise image calculated with |DWI – DWIsmoothed|. Figure A4d shows the g-factor map of four-shot MUSE, with shot-to-shot phase variations measured from 2D navigator echoes. Figure A4e shows the DWI image reconstructed by MUSE, and Figure A4f shows the corresponding noise image.

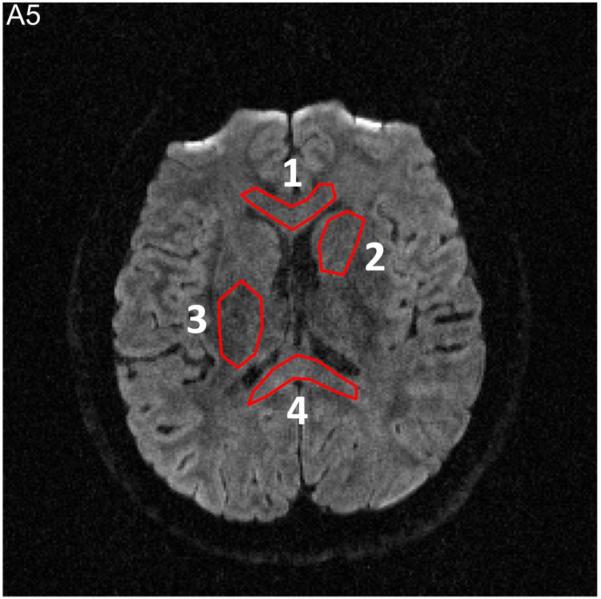
The SNR values in four ROIs (Figure A5), calculated by the ratio of “mean value of signals” (e.g., in Figure A4e) to “standard deviation of noises” (e.g., in Figure A4f) within each ROI, were then experimentally measured from SENSE and MUSE reconstructed images. The SNR difference between SENSE and MUSE reconstruction, derived from both theoretical prediction (i.e., based on g-factor maps shown in Figures A4a and A4d) and experimental measures (i.e., based on Figures A4b, A4c, A4e, A4f), are shown in Table A1.

Table A1.

ROI# SNR of SENSE SNR of MUSE SNR difference (experimental data) l/(g-factor) for SENSE l/(g-factor) for MUSE SNR difference (theoretical prediction)
1 10.18 16.13 36.88% 0.49 0.92 46%
2 8.81 15.29 42.39% 0.42 0.90 53%
3 6.89 11.36 39.39% 0.36 0.93 61%
4 9.40 16.77 43.92% 0.44 0.88 50%
Open in a new tab

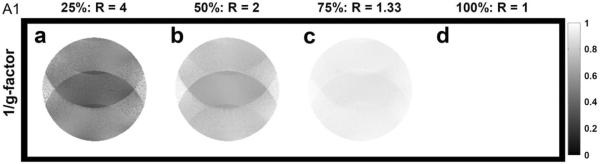
Figure A1.

Figure A1

Open in a new tab

1/(g-factor) maps of SENSE reconstruction with different acceleration factors (R=4, 2, 1.33 and 1).

Figure A2.

Figure A2

Open in a new tab

The Monte Carlo simulation results of 1/(g-factor) values for 4-shot MUSE reconstruction in the presence of random shot-to-shot phase variations.

Figure A3.

Figure A3

Open in a new tab

The sorted 1/(g-factor) values, from high to low, for four pixels shown in Figure A2.

Figure A4.

Figure A4

Open in a new tab

(a) (1/g-factor) map of SENSE reconstruction with an acceleration factor of 4. (b) DWI image reconstructed with SENSE. (c) Noise image of DWI data reconstructed with SENSE. (d) (1/g-factor) map of four-shot MUSE in the presence of shot-to-shot phase variations (measured by 2D navigator echoes). (e) DWI image reconstructed with 3D MUSE. (f) Noise image of DWI data reconstructed with 3D MUSE.

Figure A5.

Figure A5

Open in a new tab

Four ROIs used for measurement of SNR difference between SENSE (i.e., Figure A4b) and MUSE (i.e., Figure A4e) reconstruction.

Footnotes

Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.

References

  1. Bammer R. Basic principles of diffusion-weighted imaging. Eur J Radiol. 2003;45:169–184. doi: 10.1016/s0720-048x(02)00303-0. [DOI] [PubMed] [Google Scholar]
  2. Butts K, Pauly J, de Crespigny A, Moseley M. Isotropic diffusion-weighted and spiral-navigated interleaved EPI for routine imaging of acute stroke. Magn Reson Med. 1997;38:741–749. doi: 10.1002/mrm.1910380510. [DOI] [PubMed] [Google Scholar]
  3. Chang HC, Guhaniyogi S, Chen NK. Interleaved diffusion-weighted improved by adaptive partial-Fourier and multiband multiplexed sensitivity-encoding reconstruction. Magn Reson Med. 2014 doi: 10.1002/mrm.25318. doi: 10.1002/mrm.25318. [Epub ahead of print] [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Chen NK, Guidon A, Chang HC, Song AW. A robust multi-shot scan strategy for high-resolution diffusion weighted MRI enabled by multiplexed sensitivity-encoding (MUSE) Neuroimage. 2013;72:41–47. doi: 10.1016/j.neuroimage.2013.01.038. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Chu ML, Chang HC, Chung HW, Truong TK, Bashir MR, Chen NK. POCS-based reconstruction of multiplexed sensitivity encoded MRI (POCSMUSE): A general algorithm for reducing motion-related artifacts. Magn Reson Med. 2014 doi: 10.1002/mrm.25527. doi: 10.1002/mrm.25527. [Epub ahead of print] [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Engstrom M, Martensson M, Avventi E, Skare S. On the signal-to-noise ratio efficiency and slab-banding artifacts in three-dimensional multislab diffusion-weighted echo-planar imaging. Magn Reson Med. 2014 doi: 10.1002/mrm.25182. doi: 10.1002/mrm.25182. [Epub ahead of print] [DOI] [PubMed] [Google Scholar]
  7. Engstrom M, Skare S. Diffusion-weighted 3D multislab echo planar imaging for high signal-to-noise ratio efficiency and isotropic image resolution. Magn Reson Med. 2013;70:1507–1514. doi: 10.1002/mrm.24594. [DOI] [PubMed] [Google Scholar]
  8. Frank LR, Jung Y, Inati S, Tyszka JM, Wong EC. High efficiency, low distortion 3D diffusion tensor imaging with variable density spiral fast spin echoes (3D DW VDS RARE) Neuroimage. 2010;49:1510–1523. doi: 10.1016/j.neuroimage.2009.09.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Frost R, Jezzard P, Douaud G, Clare S, Porter DA, Miller KL. Scan time reduction for readout-segmented EPI using simultaneous multislice acceleration: Diffusion-weighted imaging at 3 and 7 Tesla. Magn Reson Med. 2014 doi: 10.1002/mrm.25391. doi: 10.1002/mrm.25391. [Epub ahead of print] [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Frost R, Miller KL, Tijssen RH, Porter DA, Jezzard P. 3D Multi-slab diffusion-weighted readout-segmented EPI with real-time cardiac-reordered k-space acquisition. Magn Reson Med. 2013 doi: 10.1002/mrm.25062. doi: 10.1002/mrm.25062. Epub 2013 Dec 17. [DOI] [PubMed] [Google Scholar]
  11. Guhaniyogi S, Chu ML, Chang HC, Song AW, Chen NK. Motion immune diffusion imaging using augmented MUSE for high-resolution multi-shot EPI. Magn Reson Med. 2015 doi: 10.1002/mrm.25624. DOI: 10.1002/mrm.25624. [Epub ahead of print] [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Herbst M, Zahneisen B, Knowles B, Zaitsev M, Ernst T. Prospective motion correction of segmented diffusion weighted EPI. Magn Reson Med. 2014 doi: 10.1002/mrm.25547. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Jeong HK, Gore JC, Anderson AW. High-resolution human diffusion tensor imaging using 2-D navigated multishot SENSE EPI at 7 T. Magn Reson Med. 2013;69:793–802. doi: 10.1002/mrm.24320. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Jezzard P, Barnett AS, Pierpaoli C. Characterization of and correction for eddy current artifacts in echo planar diffusion imaging. Magn Reson Med. 1998;39:801–812. doi: 10.1002/mrm.1910390518. [DOI] [PubMed] [Google Scholar]
  15. Li TQ, Kim DH, Moseley ME. High-resolution diffusion-weighted imaging with interleaved variable-density spiral acquisitions. J Magn Reson Imaging. 2005;21:468–475. doi: 10.1002/jmri.20287. [DOI] [PubMed] [Google Scholar]
  16. Liu C, Bammer R, Kim DH, Moseley ME. Self-navigated interleaved spiral (SNAILS): application to high-resolution diffusion tensor imaging. Magn Reson Med. 2004;52:1388–1396. doi: 10.1002/mrm.20288. [DOI] [PubMed] [Google Scholar]
  17. Miller KL, Pauly JM. Nonlinear phase correction for navigated diffusion imaging. Magn Reson Med. 2003;50:343–353. doi: 10.1002/mrm.10531. [DOI] [PubMed] [Google Scholar]
  18. Miller KL, Stagg CJ, Douaud G, Jbabdi S, Smith SM, Behrens TE, Jenkinson M, Chance SA, Esiri MM, Voets NL, Jenkinson N, Aziz TZ, Turner MR, Johansen-Berg H, McNab JA. Diffusion imaging of whole, post-mortem human brains on a clinical MRI scanner. Neuroimage. 2011;57:167–181. doi: 10.1016/j.neuroimage.2011.03.070. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Pipe JG, Farthing VG, Forbes KP. Multishot diffusion-weighted FSE using PROPELLER MRI. Magn Reson Med. 2002;47:42–52. doi: 10.1002/mrm.10014. [DOI] [PubMed] [Google Scholar]
  20. Porter DA, Heidemann RM. High resolution diffusion-weighted imaging using readout-segmented echo-planar imaging, parallel imaging and a two-dimensional navigator-based reacquisition. Magn Reson Med. 2009;62:468–475. doi: 10.1002/mrm.22024. [DOI] [PubMed] [Google Scholar]
  21. Pruessmann KP, Weiger M, Scheidegger MB, Boesiger P. SENSE: sensitivity encoding for fast MRI. Magn Reson Med. 1999;42:952–962. [PubMed] [Google Scholar]
  22. Skare S, Newbould RD, Clayton DB, Bammer R. Propeller EPI in the other direction. Magn Reson Med. 2006;55:1298–1307. doi: 10.1002/mrm.20890. [DOI] [PubMed] [Google Scholar]
  23. Song AW, Chang HC, Petty C, Guidon A, Chen NK. Improved delineation of short cortical association fibers and gray/white matter boundary using whole-brain three-dimensional diffusion tensor imaging at submillimeter spatial resolution. Brain Connect. 2014;4:636–640. doi: 10.1089/brain.2014.0270. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Truong TK, Chen NK, Song AW. Dynamic correction of artifacts due to susceptibility effects and time-varying eddy currents in diffusion tensor imaging. Neuroimage. 2011;57:1343–1347. doi: 10.1016/j.neuroimage.2011.06.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Truong TK, Guidon A. High-resolution multishot spiral diffusion tensor imaging with inherent correction of motion-induced phase errors. Magn Reson Med. 2013 doi: 10.1002/mrm.24709. doi: 10.1002/mrm.24709. [Epub ahead of print] [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Van AT, Aksoy M, Holdsworth SJ, Kopeinigg D, Vos SB, Bammer R. Slab profile encoding (PEN) for minimizing slab boundary artifact in three-dimensional diffusion-weighted multislab acquisition. Magn Reson Med. 2014 doi: 10.1002/mrm.25169. doi: 10.1002/mrm.25169. [Epub ahead of print] [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Van AT, Karampinos DC, Georgiadis JG, Sutton BP. K-space and image-space combination for motion-induced phase-error correction in self-navigated multicoil multishot DWI. IEEE Trans Med Imaging. 2009;28:1770–1780. doi: 10.1109/TMI.2009.2023212. [DOI] [PubMed] [Google Scholar]

RESOURCES