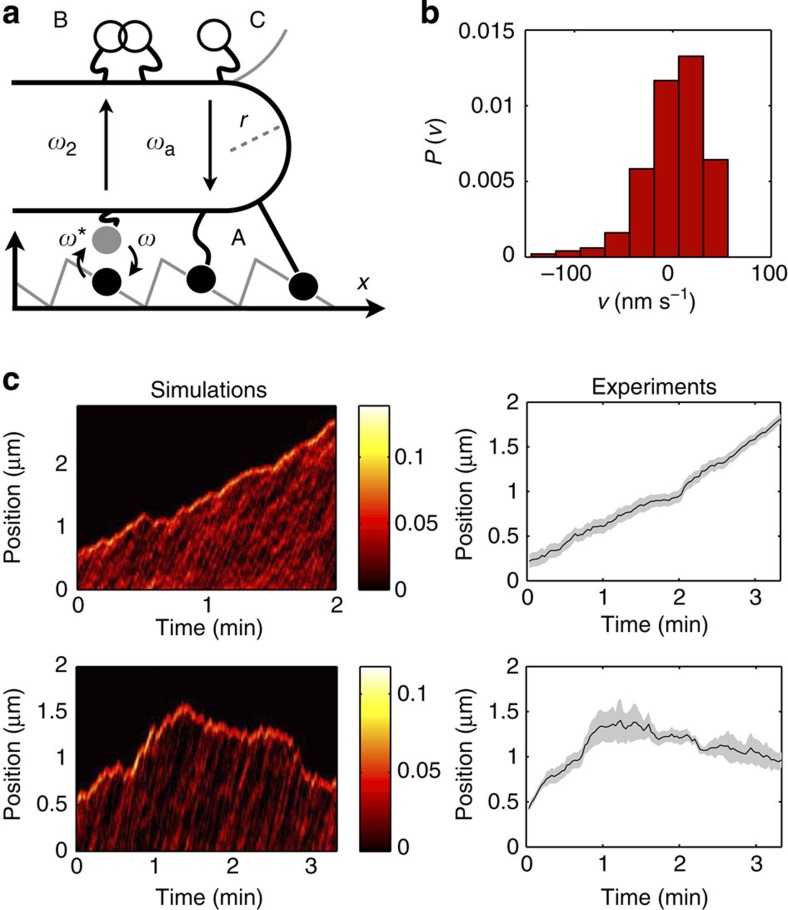
Figure 3. In silico model for longitudinal tube pulling.

(a) Schematic description of the tube tip. Three different regions can be identified (A–C). In region A, motors are either strongly bound (black circles) or weakly bound (grey circles) to the MT. They are excited and decay with average rates ω*, ω respectively. In region B, motors are detached from the MT and diffuse freely away from the tip, where overlapping is allowed. Motors switch between regions A and B with mean rates ω₂ and ω_a via detachment or attachment transitions respectively. Finally, detached motors in region C feel a soft repulsion which prevents them to enter the tip region (Supplementary Note 2). (b) Instantaneous tip velocity distribution using the data in c (bottom, left). For illustrative purposes, the time window was chosen 1 s to improve the statistics at the expense of increasing the dispersion. (c) Growth (top) and bistable motion (bottom) of a membrane tube. (Left) Simulation of the motor density plot showing tube growth with ρ_∞=1,000 μm⁻² (top) and ρ_∞=200 μm⁻² (bottom), γ=0.05 pN nm⁻¹, κ=10k_BT. The rest of parameters are specified in the Supplementary Table 1. The colour bar indicates the density of bound motors (arbitrary units). (Right) Experimental trajectories of the tube tip for 0.1 mol% biotinylated lipids. The grey region depicts the uncertainty of the tip position corresponding to 1.96 s.d. (see Methods). We find excellent quantitative agreement between velocities in experiments and in simulations.