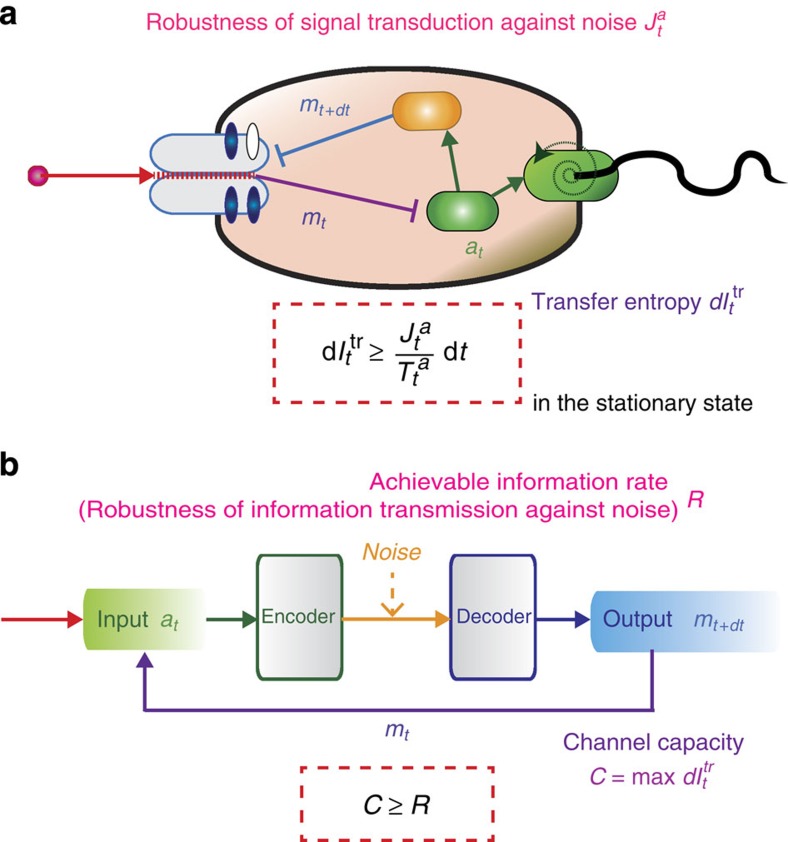
Figure 5. Analogy and difference between our approach and Shannon's information theory.

(a) Information thermodynamics for biochemical signal transduction. The robustness 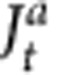is bounded by the transfer entropy 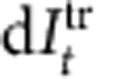in the stationary states, which is a consequence of the second law of information thermodynamics. (b) Information theory for artificial communication. The archivable information rate R, given by the redundancy of the channel coding, is bounded by the channel capacity 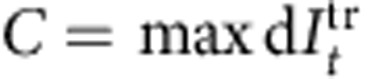, which is a consequence of the Shannon's second theorem. If the noise is Gaussian as is the case for the E. coli chemotaxis, both of the transfer entropy and the channel capacity are given by the power-to-noise ratio 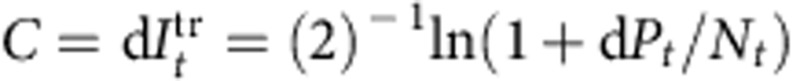, under the condition that the initial distribution is Gaussian (see Methods section).