Dose-schedule finding in phase I/II clinical trials using a Bayesian isotonic transformation

Summary

A dose-schedule-finding trial is a new type of oncology trial in which investigators aim to find a combination of dose and treatment schedule that has a large probability of efficacy yet a relatively small probability of toxicity. We demonstrate that a major difference between traditional dose-finding and dose-schedule-finding trials is that while the toxicity probabilities follow a simple nondecreasing order in dose-finding trials, those of dose-schedule-finding trials may adhere to a matrix order. We show that the success of a dose-schedule-finding method requires careful statistical modeling and a sensible dose-schedule allocation scheme. We propose a Bayesian hierarchical model that jointly models the unordered probabilities of toxicity and efficacy, and apply a Bayesian isotonic transformation to the posterior samples of the toxicity probabilities, so that the transformed posterior samples adhere to the matrix order constraints. Based on the joint posterior distribution of the order-constrained toxicity probabilities and the unordered efficacy probabilities, we develop a dose-schedule-finding algorithm that sequentially allocates patients to the best dose-schedule combination under certain criteria. We illustrate our methodology through its application to a clinical trial in leukemia, and compare it to two alternative approaches.

1 Introduction

In oncology, treatments are often administered under different schedules. For example, a patient in a certain oncology trial (further discussed in Section 5) is administered one of multiple doses of a kinase inhibitor under one of two schedules. The time over which toxicity will be assessed lasts 42 days for both schedules. In schedule 1, the kinase inhibitor is given to patients as a continuous 5-day treatment regimen with two days of rest per 7-day cycle for six cycles. In schedule 2, it is given as a continuous 15-day treatment regimen with six days of rest per 21-day cycle for two cycles. The total amount of the drug administered during the toxicity assessment window at any given dose is the same between schedules. While it may not always be true that the toxicity rate increases with schedule, in this trial schedule 2 is considered more toxic than schedule 1 due to the known pharmacokinetics of the drug. As the investigators’ goal is to find a desirable dose-schedule combination of tolerable toxicity and high efficacy, we call trials of this type dose-schedule-finding trials. Investigators at M. D. Anderson Cancer Center initiated at least one such trial per month during the period of October 2005 to September 2006.

There is a rich body of statistical literature on dose-finding methodologies accounting for toxicity and efficacy [1–5]; however, all of these studies have assumed that the schedule is fixed. Braun et al. [6,7] proposed innovative designs for finding the maximum tolerated schedule, in which schedule finding corresponds to optimizing the total number of treatment cycles given. In contrast, the schedule finding we consider attempts to determine if one method of treatment administration is better than an alternative method of treatment administration. To our knowledge, comparing and selecting doses under qualitatively different schedules remains an important open problem.

For ease of exposition, we focus on a two-schedule dose-finding design, although our method can be easily adapted to trials with multiple schedules. Specifically, suppose D doses and two different schedules are under consideration, resulting in D × 2 dose-schedule combinations.

The toxicity probabilities are assumed to follow an order constraint both within and between schedules. Specifically, we assume that toxicity increases with an increasing dose given the same schedule, and that for a given dose, toxicity increases with schedule. Based on these assumptions, the toxicity probabilities follow a matrix order [8]. Denoting p_jk as the probability of toxicity for dose j under schedule k, we have under the matrix order constraints that p_jk ≤ p_j+1,k, j = 1, …, D − 1, k = 1, 2, and p_j1 ≤ p_j2, j = 1, …, D, or equivalently, p_j1 ≤ p_j+1,1 ≤ p_j+1,2 and p_j1 ≤ p_j2 ≤ p_j+1,2. Note that the order between p_j+1,1 and p_j2 is not specified, leading to a partial order among (p_j1, p_j+1,1, p_j2, p_j+1,2).

The main challenge in dose-schedule finding is to model the matrix-ordered toxicity probabilities. Because of the matrix ordering constraints, it is not possible to combine the two sets of dose-schedule combinations into one completely ordered set. One intuitive way to model the order-constrained toxicity probabilities is to write logit(p_jk) = μ+α_j +β_k, where α_j and β_k are constrained a priori so that α_j ≤ α_j+1 for j = 1, …, D − 1 and β₁ ≤ β₂, thus constraining the probability of toxicity to increase in both dose and schedule. Although this logit model has fewer parameters, it imposes an assumption that the effects of dose and schedule on the toxicity rate are additive. Furthermore, usual order-constrained priors for α_j and β_k may lead to biased posterior estimates in the small sample context [9]. Nontrivial calibration of this type of priors is usually required in an attempt to mitigate this bias.

Assuming nondecreasing dose toxicity probabilities, Stylianou et al. [10] have used isotonic regression to calculate all the toxicity probabilities to facilitate locating the target dose following a phase I trial. To further calculate the distribution of the estimated toxicity probability at the recommended dose, they proposed a bootstrap method. While their bootstrap method may perform well in estimating the distribution of the estimated toxicity probability at the target dose, computational constraints limit its use in repeated calculation of the distributions of the estimated toxicity probabilities at multiple dose-schedule combinations at every assessment point of a dose-schedule-finding trial.

A related problem to dose-schedule finding is dose finding for ordered groups [11–13]. While these two problems involve the same issue of modeling matrix-ordered toxicity probabilities, a phase I/II dose-schedule-finding design has two important distinctions from a dose-finding design for ordered groups. First, the goal of a dose-schedule-finding trial is to recommend a desirable dose-schedule combination with high efficacy and low toxicity, while that of a dose-finding trial with ordered groups is to identify a desirable dose within each group. Consequently, different decision rules are required. Second, our method simultaneously monitors toxicity and efficacy outcomes while [11–13] model toxicity outcomes alone.

Our proposed design consists of three elements: a bivariate binary model, a Bayesian isotonic transformation (BIT) with respect to matrix ordering, and a dose-schedule-finding algorithm. Specifically, to estimate the joint posterior distribution of the matrix-ordered toxicity probabilities and the unordered efficacy probabilities, we first implement the global cross-ratio model [14] for the unordered toxicity and efficacy probabilities; we then, by regarding the order-constrained toxicity probabilities as an isotonic transformation of the unordered toxicity probabilities, extend the BIT by Dunson and Neelon [9] to the case of matrix ordering. To compute the isotonic regression transformation for each unordered posterior sample of the toxicity probabilities, we use the minimum lower sets algorithm (MLSA) [15]. The joint posterior distribution of the order-constrained toxicity probabilities and the unordered efficacy probabilities is thus estimated based on these order-constrained posterior samples of the toxicity probabilities and the posterior samples of the remaining unordered parameters. With this estimated joint posterior distribution, we develop a dose-schedule-finding algorithm to sequentially allocate patients to dose-schedule combinations of potential and make a final recommendation of the combination at the end of the trial.

The remainder of the article is organized as follows. In Section 2, we present the probability model, including the likelihood, priors and posteriors. We introduce the BIT approach in Section 3 and the dose-schedule-finding algorithm in Section 4. In Section 5, we introduce a motivating example and compare the operating characteristics of the proposed design with those of two alternative approaches. We provide concluding remarks in Section 6. In Section 7, we present appendices that illustrate the MLSA and its computational aspects, and describe in detail two alternative designs used for comparison to our proposed design.

2 Probability model

We assume there are D doses and that each dose may be administered under two different schedules. Let (j, k) represent dose j under schedule k, j = 1, …, d and k = 1, 2. Denote X_ijk as the binary toxicity outcome for subject i administered at dose-schedule combination (j, k), and Y_ijk as the binary efficacy outcome for the same subject. We assume that X_ijk = 1 with probability p_jk and that Y_ijk = 1 with probability q_jk. Let n_jk denote the number of subjects that have been currently treated at dose j under schedule k. We formulate the global cross-ratio model [14] for the bivariate toxicity and efficacy outcomes as follows: Define ${\pi }_{xy}^{(jk)}=Pr(X_{\mathit{ijk}}=x,Y_{\mathit{ijk}}=y)$, x, y = 0, 1, to be the joint probability of the toxicity and efficacy outcomes, and let

$${\theta }_{jk}=\frac{{\pi }_{00}^{(jk)}{\pi }_{11}^{(jk)}}{{\pi }_{01}^{(jk)}{\pi }_{10}^{(jk)}}$$

quantify the association between the two outcomes. Then the cell probabilities ${\pi }_{xy}^{(jk)}$ can be obtained from p_jk, q_jk, and θ_jk by

$$\begin{array}{c}{\pi }_{11}^{(jk)}=\{\begin{array}{ll}\left(a_{jk}-\sqrt{a_{jk}^2+b_{jk}}\right)/\{2({\theta }_{jk}-1)\}\hfill & {\theta }_{jk}\ne 1\hfill \\ p_{jk}{q}_{jk}\hfill & {\theta }_{jk}=1,\hfill \end{array}\\ {\pi }_{10}^{(jk)}=p_{jk}-{\pi }_{11}^{(jk)},{\pi }_{01}^{(jk)}=q_{jk}-{\pi }_{11}^{(jk)},{\pi }_{00}^{(jk)}=1-p_{jk}-q_{jk}+{\pi }_{11}^{(jk)},\end{array}$$ (1)

where a_jk = 1 + (p_jk + q_jk)(θ_jk − 1) and b_jk = −4θ_jk(θ_jk − 1)p_jkq_jk.

We further define μ_jk and γ_jk as follows:

$${\mu }_{jk}=\text{logit}(p_{jk})\text{and}{\gamma }_{jk}=\text{logit}(q_{jk}).$$ (2)

Denoting μ = (μ₁₁, …, μ_D1, μ₁₂, …, μ_D2)′, γ = (γ₁₁, …, γ_D1, γ₁₂, …, γ_D2)′ and θ = (θ₁₁, …, θ_D1, θ₁₂, …, θ_D2)′, the contribution of dose-schedule combination (j, k) to the likelihood is given as

$$L_{jk}(\mathit{\mu },\mathit{\gamma },\mathit{\theta })=\prod _{i=1}^{n_{jk}}{\{{\pi }_{00}^{(jk)}\}}^{(1-x_{\mathit{ijk}})(1-y_{\mathit{ijk}})}{\{{\pi }_{10}^{(jk)}\}}^{x_{\mathit{ijk}}(1-y_{\mathit{ijk}})}{\{{\pi }_{01}^{(jk)}\}}^{(1-x_{\mathit{ijk}})y_{\mathit{ijk}}}{\{{\pi }_{11}^{(jk)}\}}^{x_{\mathit{ijk}}{y}_{\mathit{ijk}}},$$ (3)

where x_ijk and y_ijk are the observed efficacy and toxicity outcomes for the ith patient treated at dose j and schedule k. The full likelihood, denoted as L(μ, γ, θ), is the product of L_jk’s over all dose-schedule combinations that have currently been evaluated.

To specify the priors, we assume that μ_jk, γ_jk and θ_jk are mutually independent, and their priors are given by ${\mu }_{jk}~\mathrm{N}(0,{\sigma }_{\mu }^2),{\gamma }_{jk}~\mathrm{N}(0,{\sigma }_{\gamma }^2)$, and $log{\theta }_{jk}~N(0,{\sigma }_{\theta }^2)$, where ${\sigma }_{\mu }^2,{\sigma }_{\gamma }^2$ and ${\sigma }_{\theta }^2$ are prior variances taking large values (e.g., ${\sigma }_{\mu }^2={\sigma }_{\gamma }^2={10}^4$ and ${\sigma }_{\theta }^2=10$).

At any point of the trial, let h₁ and h₂ denote the highest tried doses of schedules 1 and 2, respectively. The highest tried dose under a schedule refers to the highest dose at which at least one cohort of patients has been treated under the schedule. If no dose has been tried under schedule k, we then define h_k = 0. We assume that the starting combination is (1, 1), i.e., the lowest dose under schedule 1. Therefore, we always have h₁ ≥ 1 and h₂ ≥ 0, if at least one cohort of patients has been treated. Note that only the parameters associated with tried dose-schedule combinations appear in the full likelihood. We therefore define μ^(h₁h₂) = (μ₁₁, …, μ_h11, μ₁₂, …, μ_h22)′, γ^(h₁h₂) = (γ₁₁, …, γ_h11, γ₁₂, …, γ_h22)′ and θ^(h₁h₂) = (θ₁₁, …, θ_h11, θ₁₂, …, θ_h22)′. The joint posterior distribution is then given by

$$g\left({\mathit{\mu }}^{(h_1{h}_2)},{\mathit{\gamma }}^{(h_1{h}_2)},{\mathit{\theta }}^{(h_1{h}_2)}\mid \text{Data}\right)\propto L(\mathit{\mu },\mathit{\gamma },\mathit{\theta })·\pi \left({\mathit{\mu }}^{(h_1{h}_2)}\right)\pi \left({\mathit{\gamma }}^{(h_1{h}_2)}\right)\pi \left({\mathit{\theta }}^{(h_1{h}_2)}\right),$$ (4)

where π(μ^(h₁h₂)), π(γ^(h₁h₂)), and π(θ^(h₁h₂)) are the prior densities for μ^(h₁h₂), γ^(h₁h₂), and θ^(h₁h₂), respectively.

Given the joint posterior distribution, all full conditional distributions for Gibbs sampling can be derived in a straightforward manner. To sample from these full conditional distributions, we use the adaptive rejection Metropolis sampling (ARMS) algorithm [16]. Although it is possible to sample the toxicity and efficacy probabilities directly, the transformations given in (2) resulted in increased numerical stability when using the ARMS algorithm.

3 Bayesian isotonic transformation

The probabilities of toxicity p_jk are assumed to follow the matrix ordering exemplified by p_jk ≤ p_j+1,k and p_jk ≤ p_j,k+1, as previously discussed. Because the transformation of p_jk in (2) is monotone, the μ_jk’s follow the same order

$${\mu }_{jk}\le {\mu }_{j+1,k}\text{and}{\mu }_{jk}\le {\mu }_{j,k+1}.$$ (5)

To make order-restricted inference on μ, we propose a Bayesian isotonic transformation (BIT) that extends the approach in the simple-order setting in Dunson and Neelon [9] to one that accounts for matrix ordering. Although a similar ordering assumption may be plausible for the efficacy probabilities, such an assumption does not always hold, especially for cytostatic agents. It has been documented that the efficacy probability may not increase beyond certain dose levels. See, e.g., [17–19]. Nevertheless, if there is strong prior information that efficacy increases with dose, then our method can be modified so that a BIT is applied to both toxicity and efficacy. We should note that such an increasing efficacy assumption should be used with caution since it could lead to an aggressive design by encouraging escalation and thus potentially exposing more patients to toxic dose-schedule combinations.

Let C = {(j, k) : j = 1, …, h_k, k = 1, 2} be the set of all tried dose-schedule combinations. Define an order ⪯ on C as follows:

$$(j_1,k_1)\preccurlyeq (j_2,k_2)\text{if}{j}_1\le j_2\text{and}{k}_1\le k_2.$$ (6)

It is straightforward to verify that C is a partially-ordered set (see the formal definition of a partial order in [15]).

Given the above definition of C with order ⪯, an unconstrained draw μ̃ of μ from its posterior (4) can be regarded as a real-valued function on C, and the isotonic regression μ̃^* of μ̃ is an isotonic function that minimizes the weighted sum of squares

$$\sum _{(j,k)\in C}{({\stackrel{\sim }{\mu }}_{jk}-{\stackrel{\sim }{\mu }}_{jk}^{\ast })}^2{w}_{jk},$$ (7)

subject to the constraints ${\stackrel{\sim }{\mu }}_{j_1{k}_1}^{\ast }\le {\stackrel{\sim }{\mu }}_{j_2{k}_2}^{\ast }$ whenever (j₁, k₁) ⪯ (j₂, k₂). The weights {w_jk, j = 1, …, h_k, k = 1, 2} are taken to be the posterior precisions of μ_jk. Note Equation (7) implies that this isotonic regression transformation of μ is a minimal distance mapping from the unconstrained to the constrained parameter space.

Directly calculating the isotonic regression μ̃^* using the min-max formula in [15] for a partially-ordered set is computationally burdensome. An improved strategy is the following three-step approach: first, enumerate all simple orders nested within the matrix order, then apply the pool-adjacent-violators algorithm (PAVA) under each simple order, and lastly, find the “best” estimates among them [8]. In the context of dose-schedule finding, such an approach is also computationally intensive due to the large number of enumerations required to completely order the dose-schedule combinations. We apply an alternative algorithm, the minimum lower sets algorithm (MLSA) [15], to compute the isotonic regression μ̃^*. For a general description of the algorithm, see [15]. In Appendices 1 and 2, we provide a simplistic example to illustrate the algorithm and summarize its computational properties. Additional details of the algorithm specific to the matrix ordering are available from the first author upon request.

Overview of computational steps

To clarify our algorithm, we present the reader with an outline of the computational steps involved in the estimation of model parameters.

1. For each dose-schedule combination, obtain samples from the posterior distributions of (μ_jk, γ_jk, θ_jk) via the ARMS Markov chain Monte Carlo (MCMC).

2. For each realization μ̃ from the unconstrained joint posterior distribution of μ obtained in step 1, use the MLSA to obtain the order-restricted posterior sample μ̃^*.

3. Obtain the order-restricted posterior samples of p_jk by taking the transformations ${\mathit{logit}}^{-1}({\stackrel{\sim }{\mu }}_{jk}^{\ast })$, and similarly obtain the unconstrained posterior samples of q_jk and θ_jk.

4. Obtain posterior samples of ${\pi }_{xy}^{(jk)}$, if necessary, based on the samples of p_jk, q_jk and θ_jk for x = 0, 1, y = 0, 1, using (1).

As can be seen from the steps above, the isotonic regression is performed after obtaining all samples from the unconstrained posterior via MCMC. Because the isotonic regression as a minimal distance mapping is a measurable function, and a measurable function of a random variable is itself a random variable, the isotonically transformed sample μ̃^* together with the untransformed samples γ̃ and θ̃ can be considered a random sample from a constrained joint posterior distribution of (μ, γ, θ). Using (1) and (2), Bayesian inference on the joint posterior distribution of the order-constrained toxicity probabilities and the unordered efficacy probabilities can then proceed based on these order-constrained posterior samples of μ and the unordered posterior samples of γ and θ.

4 Dose-schedule-finding algorithm

We propose an algorithm that sequentially allocates new patients to dose-schedule combinations that are safe and efficacious. The allocation scheme is based on the constrained joint posterior distribution of toxicity and efficacy probabilities at each dose-schedule combination. All accumulated data are used in the estimation procedure under the Bayesian model.

We first define a target dose-schedule combination, i.e., a combination at which the toxicity probability p_jk ≤ p̄ and the efficacy probability q_jk ≥ q, where p̄ and q are physician-specified upper limit for toxicity (e.g., 0.3) and lower limit for efficacy (e.g., 0.3), respectively. Given this definition, we select the dose-schedule combination at the end of the trial that maximizes the posterior probability Pr(p_jk ≤ p̄, q_jk ≥ q | Data). Note that this criterion has a decision-theoretic justification since it is equivalent to maximizing the posterior expected utility with the utility function defined as I(p_jk ≤ p̄, q_jk ≥ q), where I(·) is an indicator function.

Before describing the proposed dose-schedule-finding algorithm, we categorize a dose-schedule combination as having negligible, acceptable, or unacceptable toxicity as follows.

• A dose-schedule combination (j, k) has negligible toxicity if Pr(p_jk ≤ p̄ | Data) > P_n, where P_n is a chosen probability cutoff with a relatively large value (say, 0.5). By this definition, a dose-schedule combination has negligible toxicity when there is a relatively large posterior probability that its toxicity probability is less than the upper limit p̄.

• A dose-schedule combination (j, k) has acceptable toxicity if Pr(p_jk ≤ p̄|Data) > P_a, where P_a is a cutoff smaller than P_n (say, 0.05). Therefore, that a dose-schedule combination has negligible toxicity implies that it has acceptable toxicity.

• A dose-schedule combination (j, k) has unacceptable toxicity if Pr(p_jk ≤ p̄| Data) ≤ P_a. By this definition, when there is a small posterior probability that the toxicity probability is less than or equal to the upper limit p̄, the dose-schedule combination is very likely to be highly toxic, therefore it is considered unacceptable with high toxicity.

These rules for defining negligible, acceptable, and unacceptable toxicity are not standard, but they are consistent with the preferences of clinical investigators. Typically, investigators are willing to try higher dose-schedule combinations only after seeing evidence that previously tried lower dose-schedule combinations are safe (i.e., have negligible toxicity). Alternatively, they want to continue learning about the toxicity profile of dose-schedule combinations with acceptable toxicity.

In addition to the above categorization based on toxicity, each dose-schedule combination is deemed to have acceptable efficacy if the posterior probability that its efficacy probability is at least as large as q is greater than a certain cutoff (say, 0.02). Mathematically, if Pr(q_jk ≥ q | Data) > Q_a for some small cutoff Q_a ∈ (0, 1), then the dose-schedule combination has acceptable efficacy. A dose-schedule combination is deemed acceptable if it has both acceptable toxicity and efficacy.

We propose an algorithm that finds a target dose-schedule combination with a probability of toxicity less than or equal to 0.3 and a probability of efficacy greater than or equal to 0.3. First, we introduce some notation. Let

$$\mathcal{A}=\{(j,k):(j,k)\text{is}\mathit{acceptable},1\le j\le h_k,k=1,2\}$$

denote the set of all acceptable dose-schedule combinations that have been tried (recall that h₁ and h₂ denote the highest tried doses in schedules 1 and 2, respectively). Let ${\widehat{\pi }}_{01}^{(jk)}={\widehat{q}}_{jk}-{\widehat{\pi }}_{11}^{(jk)}$ be an estimate of ${\pi }_{01}^{(jk)}$, in which q̂_jk is the posterior mean of q_jk and ${\widehat{\pi }}_{11}^{(jk)}$ is a plug-in estimate of ${\pi }_{11}^{(jk)}$ (i.e., replacing p_jk with the mean of its isotonically transformed posterior samples, and q_jk and θ_jk with their posterior means in (1)). A large value of ${\widehat{\pi }}_{01}^{(jk)}$ implies a large probability of efficacy and no toxicity. With the goal of finding a target dose-schedule combination, we propose the following dose-schedule-finding algorithm:

1. As general rules, under a given schedule a dose is never skipped; in addition, for a fixed dose a schedule is never skipped. If the lowest combination (1, 1) has unacceptable toxicity, or the maximum sample size is reached, the trial is terminated.

2. Start treating patients at (1, 1). If (1, 1) has negligible toxicity, the next cohort of patients is treated at (1, 2).

3. When h₁ < D and h₂ < D,

   1. if both (h₁, 1) and (h₂, 2) have negligible toxicity, the next cohort of patients is treated at (h₁+1, 1) or (h₂+1, 2), depending on which of the probabilities Pr(p_hk,k ≤ p̄| Data), k = 1, 2, is larger;

   2. if only (h₁, 1) has negligible toxicity, the next cohort of patients is treated at (h₁ + 1, 1); if instead only (h₂, 2) has negligible toxicity, the next cohort of patients is treated at (h₂ + 1, 2);

   3. if neither (h₁, 1) nor (h₂, 2) has negligible toxicity, the next cohort of patients is treated at the dose-schedule combination in that has the largest value of ${\widehat{\pi }}_{01}^{(jk)}$, or the trial is terminated if is empty.

4. When h₁ = D and h₂ < D, if (h₂, 2) has negligible toxicity, the next cohort of patients is treated at (h₂ + 1, 2). Otherwise, the next cohort of patients is treated at the dose-schedule combination in 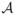that has the largest value of ${\widehat{\pi }}_{01}^{(jk)}$, or the trial is terminated if 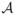is empty.

5. When h₁ = h₂ = D, the next cohort of patients is treated at the dose-schedule combination in 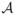that has the largest value of ${\widehat{\pi }}_{01}^{(jk)}$, or the trial is terminated if 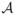is empty.

6. At the end of the trial, the dose-schedule combination in with the largest value of Pr(p_jk ≤ p̄, q_jk ≥ q | Data) is selected as the recommended combination.

Note that the case where h₁ < D and h₂ = D is not discussed above. This is because dose D under schedule 2 cannot be tried without having first tried dose D under schedule 1, based on the general rules specified in step 1. In fact, based on the order assumption that schedule 2 is at least as toxic as schedule 1 at any given dose, the estimated toxicity probability for a dose under schedule 1 cannot be larger than that for the same dose under schedule 2. This, combined with rules 2 and 3(a) in the algorithm, makes it impossible to have a larger h₂ than h₁. In other words, our algorithm will not treat patients at a dose under schedule 2, which is more toxic, without treating patients at the same dose under schedule 1 first.

5 Application and Simulation

Our proposed design was motivated by a clinical trial of a kinase inhibitor in patients with acute leukemia, myelodysplastic syndromes, or chronic myeloid leukemia in blast phase. These diseases have been found to be associated with unregulated kinase activity. Thus, the kinase inhibitors are an important set of treatment options for hematologic malignancies. The goal of this trial was to assess five doses of a kinase inhibitor administered under two different treatment schedules, a continuous 5-day administration with a 2-day rest per week for six weeks (schedule 1), and a continuous 15-day administration with a 6-day rest per 21-day cycle for two cycles (schedule 2).

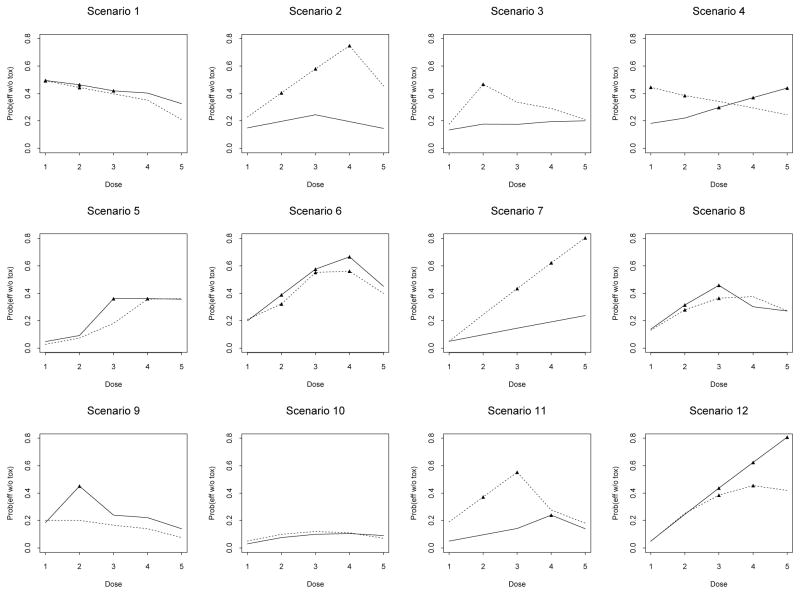
Based on this trial, we constructed 12 scenarios with different true probabilities of toxicity and efficacy across the dose-schedule combinations (Figure 1). The toxicity and efficacy outcomes were assumed to be independent. Therefore, for example, the joint probability of efficacy and no toxicity is the product of the marginal probability of efficacy and (1 − the marginal probability of toxicity). The maximum sample size chosen for the simulations was 60. The toxicity upper limit and efficacy lower limit were taken to be p̄ = q = 0.3, and the chosen cutoff probabilities were P_n = 0.5, P_a = 0.05 and Q_a = 0.02. Under each scenario, we simulated 1,000 trials.

Figure 1.

Scenarios in the simulation study for the leukemia trial: —— schedule 1; . . . . . . schedule 2. There are five doses (horizontal axis) in each schedule. The vertical axis is the joint probability of efficacy without toxicity. Points marked by black triangles correspond to the target dose-schedule combinations, at which the probability of toxicity does not exceed 0.3 and the probability of efficacy is at least 0.3.

After obtaining 6,000 Gibbs samples from the posterior density (4), we discarded the first 1,000 samples (burn-in), recorded every fifth subsequent sample to reduce the autocorrelation in the Markov chain, applied the isotonic transformations to the samples of μ_jk, and then implemented the proposed dose-schedule-finding algorithm. The Markov chains converged fast and mixed well.

For comparison purposes, we implemented two alternative designs. The first method performs dose finding independently under each schedule based on efficacy and toxicity responses, using a Bayesian isotonic transformation (BIT) for toxicity. We call this design the one-dimensional BIT design, and accordingly, we call our proposed design the two-dimensional BIT design. Details of the one-dimensional BIT design are given in Appendix 3.

The second method is a two-stage design in which we use the Continual Reassessment Method (CRM, [20]) in the first stage to independently locate the MTD under each schedule, and then adaptively randomize (AR) patients over all dose-schedule combinations at or below the MTDs in the second stage. We name this method the CRM + AR design. We use rule 6 of the dose-schedule-finding algorithm in Section 4 for the final selection of a dose-schedule combination. Details of the CRM + AR design are given in Appendix 4.

We summarize the operating characteristics of all three designs under the 12 scenarios in Table 1, which is organized in scenario sections. For each scenario section, the first and sixth rows detail the pair of true marginal probabilities of toxicity and efficacy (multiplied by 100) for schedules 1 and 2, respectively; the second and seventh rows detail the true joint probabilities of efficacy and no toxicity; the third and eighth rows detail the selection percentages of the doses in schedules 1 and 2 using the two-dimensional BIT design (BIT-2d), with the average numbers of patients treated at each dose-schedule combination given in parentheses; the fourth and ninth rows and the fifth and 10th rows are analogous to the results presented in the third and eighth rows, differing only in that they summarize the operating characteristics of the one-dimensional BIT design (BIT-1d) and the CRM+AR design, respectively. The columns labeled “Sce” and “Sch” indicate the scenarios and schedules, respectively. The “None” column represents the percentages of the 1,000 simulated trials in which no dose-schedule combinations were selected due to either excessive toxicity or a lack of response, i.e., inconclusive trials. The last two columns give the observed toxicity and efficacy percentages out of the 1,000 simulated trials.

Table 1.

Selection percentage of dose-schedule combination and number of patients treated for the leukemia trial. “Sce” and “Sch” denote the scenario and schedule numbers, respectively. Each pair in parentheses denotes the true probabilities of toxicity and efficacy (multiplied by 100) for the dose-schedule combination with the schedule given in the same row and the dose specified above in the same column. The underlined pairs are target dose-schedule combinations with a toxicity probability ≤ 0.3 and an efficacy probability ≥ 0.3. π₀₁ represents the joint probability of efficacy and no toxicity. Independence between toxicity and efficacy responses is assumed in generating the data. “None” denotes the percentage of the times that no combination is selected. “Tox” denotes the overall percentage of toxicity. “Eff” denotes the overall percentage of efficacy.

Dose
Sce	Sch	1	2	3	4	5	None	Tox	Eff
1	1	(10, 55)	(20, 58)	(30, 60)	(35, 62)	(50, 65)
π01		.50	.46	.42	.40	.33
BIT-2d		41.1 (15.4)	23.7 (11.6)	4.5 (6.7)	.7 (3.8)	0 (1.5)
BIT-1d		42.9 (15.8)	11.9 (7.9)	1.7 (3.7)	.2 (1.8)	0 (.7)
CRM+AR		38.3 (11)	13.9 (8.3)	4.5 (7.2)	1.1 (3.9)	.3 (1.1)
1	2	(15, 58)	(25, 59)	(35, 61)	(45, 64)	(70, 70)
π01		.49	.44	.40	.35	.21
BIT-2d		25.0 (11.9)	4.8 (6.0)	0 (2.3)	0 (.7)	0 (.1)	.2	20	58
BIT-1d		38.4 (18.7)	4.4 (6.7)	.5 (2.8)	0 (1.1)	0 (.3)	0	19	58
CRM+AR		30.7 (12)	8.0 (7.7)	2.7 (5.6)	.5 (2.4)	0 (.4)	0	23	59
2	1	(1, 15)	(1.5, 20)	(2, 25)	(2.5, 20)	(3, 15)
π01		.15	.20	.25	.20	.15
BIT-2d		.4 (3.7)	1.7 (3.9)	3.5 (4.7)	1.9 (3.9)	.4 (3.4)
BIT-1d		.7 (5.4)	1.7 (5.9)	3.1 (7.9)	1.6 (5.9)	.9 (4.7)
CRM+AR		.7 (4.6)	2.5 (4.8)	4.0 (5.3)	1.2 (5.0)	.2 (7.1)
2	2	(9, 25)	(10, 45)	(11, 65)	(12, 85)	(35, 70)
π01		.23	.41	.58	.75	.46
BIT-2d		2.2 (4.0)	11.0 (5.7)	29.1 (9.2)	49.1 (17.7)	.3 (3.7)	.4	9	52
BIT-1d		3.9 (5.4)	20.5 (6.8)	36.8 (8.0)	30.5 (7.0)	.3 (2.3)	0	7	39
CRM+AR		2.5 (6.9)	15.8 (6.8)	29.8 (7.5)	41.0 (7.5)	2.2 (7.5)	.1	9	40
3	1	(10, 15)	(12, 20)	(30, 25)	(35, 30)	(50, 40)
π01		.14	.18	.18	.20	.20
BIT-2d		3.8 (5.6)	5.8 (6.0)	6.9 (5.3)	3 (3.7)	.2 (1.7)
BIT-1d		2.0 (8.6)	4.3 (8.4)	3.3 (6.3)	2.0 (3.4)	0 (1.1)
CRM+AR		2.7 (7.3)	6.4 (7.2)	3.7 (7.3)	2.6 (4.4)	.2 (1.5)
3	2	(12, 20)	(15, 55)	(40, 56)	(50, 58)	(70, 70)
π01		.18	.47	.34	.29	.21
BIT-2d		4.8 (5.5)	68.3 (22.7)	2.9 (6.1)	0 (1.3)	0 (.1)	4.3	21	40
BIT-1d		5.9 (6.6)	75.3 (17.6)	6.4 (4.7)	.3 (1.6)	0 (.4)	.5	20	35
CRM+AR		5.2 (9.0)	69.2 (13)	6.6 (7.4)	1.5 (2.6)	.8 (.4)	1.1	22	35
4	1	(9, 20)	(12, 25)	(15, 35)	(18, 45)	(20, 55)
π01		.18	.22	.30	.37	.44
BIT-2d		2.1 (4.6)	3.9 (4.5)	9.9 (5.9)	15.3 (7.1)	12.5 (7.4)
BIT-1d		1.3 (7.1)	2.9 (6.3)	7.0 (6.4)	6.9 (5.5)	4.7 (3.6)
Ind YLJ		3.7 (5.4)	3.6 (5.1)	5.6 (5.2)	11.4 (6.0)	17.9 (6.6)
CRM+AR		1.7 (6.8)	3.9 (5.7)	7.7 (6.9)	13.0 (6.6)	9.7 (4.9)
4	2	(11, 50)	(30, 55)	(40, 57)	(50, 59)	(60, 61)
π01		.45	.39	.34	.30	.24
BIT-2d		41.3 (15.2)	10.6 (8.6)	.9 (3.6)	.1 (1.0)	0 (.2)	3.4	19	45
BIT-1d		65.1 (19.6)	11.0 (7.5)	1.1 (2.8)	0 (.9)	0 (.2)	0	17	43
CRM+AR		52.2 (13)	9.5 (9.1)	1.7 (5.4)	.4 (1.6)	.1 (.2)	.1	20	44
5	1	(5, 5)	(8, 10)	(10, 40)	(28, 50)	(49, 70)
π01		.05	.09	.36	.36	.36
BIT-2d		1.2 (3.6)	1.7 (3.9)	50.9 (14.5)	35.6 (13.0)	1.4 (7.4)
BIT-1d		.3 (4.1)	2.1 (4.2)	51.4 (10.6)	28.0 (6.9)	2.7 (2.6)
CRM+AR		.1 (4.8)	1.7 (5.1)	55.6 (11)	23.5 (9.2)	3.7 (3.9)
5	2	(8, 3)	(9, 8)	(10, 20)	(49, 70)	(60, 90)
π01		.03	.08	.18	.36	.36
BIT-2d		.8 (3.3)	1.6 (3.5)	4.3 (4.2)	0 (2.4)	0 (3.1)	2.5	20	38
BIT-1d		.2 (5.0)	1.2 (5.8)	11.1 (9.2)	.1 (3.1)	1.5 (5.6)	1.4	18	31
CRM+AR		.2 (5.1)	.4 (4.9)	8.2 (7.7)	3.8 (6.5)	1.5 (1.5)	1.3	20	34
6	1	(1, 20)	(3, 40)	(4, 60)	(5, 70)	(40, 75)
π01		.20	.39	.58	.67	.45
BIT-2d		.7 (3.5)	4.4 (4.7)	29.8 (10.8)	47.3 (14.8)	.4 (5.1)
BIT-1d		.2 (3.6)	8.1 (5.7)	34.0 (8.8)	35.2 (8.7)	.2 (3.2)
CRM+AR		.5 (4.6)	7.5 (5.7)	25.5 (6.8)	38.6 (7.7)	.9 (6.8)
6	2	(5, 22)	(8, 35)	(15, 65)	(20, 70)	(50, 80)
π01		.21	.32	.55	.56	.40
BIT-2d		.6 (3.3)	1.2 (3.8)	11.6 (7.0)	3.4 (4.8)	0 (1.9)	.6	11	59
BIT-1d		.7 (5.4)	3.3 (6.8)	14.8 (9.9)	3.5 (5.1)	0 (2.1)	0	11	54
CRM+AR		.5 (5.3)	3.3 (5.5)	13.5 (7.3)	9.7 (6.9)	0 (3.4)	0	14	55
7	1	(1, 5)	(2, 10)	(3, 15)	(4, 20)	(5, 25)
π01		.05	.10	.15	.19	.24
BIT-2d		0 (3.1)	0 (3.1)	.2 (3.3)	.4 (3.4)	.8 (3.5)
BIT-1d		0 (4.0)	.1 (4.8)	.3 (5.6)	.8 (7.4)	1.2 (7.8)
CRM+AR		0 (3.8)	0 (4.0)	.1 (4.5)	.3 (4.9)	.5 (7.8)
7	2	(1.5, 5)	(2.5, 25)	(3.5, 45)	(4.5, 65)	(5.5, 85)
π01		.05	.24	.43	.62	.80
BIT-2d		0 (3.0)	.6 (3.5)	6.7 (5.3)	29.4 (10.7)	61.4 (20.9)	.5	4	51
BIT-1d		0 (3.1)	1.3 (3.7)	13.8 (5.6)	41.2 (8.8)	41.3 (8.8)	0	4	36
CRM+AR		0 (3.8)	.8 (5.1)	8.9 (6.9)	24.9 (11.0)	64.5 (8.2)	0	4	39
8	1	(8, 15)	(10, 35)	(12, 52)	(45, 55)	(55, 60)
π01		.14	.32	.46	.30	.27
BIT-2d		2 (4.4)	21.4 (9.3)	53.8 (18.5)	1 (6.4)	0 (2.1)
BIT-1d		1.3 (4.9)	22.2 (8.5)	47.2 (10.6)	2.5 (3.5)	.3 (1.2)
CRM+AR		1.3 (6.4)	20.8 (8.2)	52.8 (11)	1.9 (6.2)	.1 (1.7)
8	2	(13, 15)	(20, 35)	(30, 52)	(50, 75)	(65, 78)
π01		.13	.28	.36	.38	.27
BIT-2d		1.6 (3.7)	8.8 (5.5)	7.4 (5.8)	0 (2.0)	0 (.1)	4.0	21	44
BIT-1d		1.4 (6.9)	15.0 (11.9)	9.8 (7.5)	.2 (2.1)	0 (.4)	.1	20	40
CRM+AR		1.0 (7.9)	10.4 (8.2)	10.4 (7.1)	1.0 (3.1)	0 (.5)	.3	22	40
9	1	(8, 20)	(10, 50)	(40, 40)	(45, 40)	(60, 35)
π01		.18	.45	.24	.22	.14
BIT-2d		6 (6.8)	84.7 (33.9)	4.9 (6.8)	.6 (3.0)	0 (.6)
BIT-1d		8.6 (6.2)	78.3 (16.0)	6.8 (4.5)	1.4 (2.0)	0 (.5)
CRM+AR		3.2 (9.5)	88.2 (21.0)	2.3 (9.0)	.9 (3.7)	.3 (.8)
9	2	(50, 40)	(60, 50)	(70, 55)	(80, 70)	(90, 75)
π01		.20	.20	.17	.14	.08
BIT-2d		1.3 (5.7)	.1 (1.9)	0 (.2)	0 (0)	0 (0)	2.4	21	44
BIT-1d		1.3 (13.8)	0 (2.2)	0 (.2)	0 (0)	0 (0)	3.6	29	41
CRM+AR		.6 (14)	.3 (1.1)	.2 (.2)	.7 (0)	.5 (0)	2.8	27	41
10	1	(40, 5)	(50, 15)	(60, 25)	(70, 35)	(80, 45)
π01		.03	.08	.10	.11	.09
BIT-2d		1.4 (7.1)	.6 (4.5)	.2 (1.0)	0 (.1)	0 (.0)
BIT-1d		2.2 (7.2)	5.5 (4.4)	.8 (.8)	0 (.1)	0 (0)
CRM+AR		0 (14)	0 (2.4)	0 (.7)	.4 (.1)	.2 (.1)
10	2	(50, 10)	(60, 25)	(70, 40)	(80, 55)	(90, 70)
π01		.05	.10	.12	.11	.07
BIT-2d		.2 (3.6)	0 (.8)	0 (.0)	0 (0)	0 (0)	97.6	47	11
BIT-1d		.9 (7.9)	.2 (2.7)	0 (.2)	0 (.0)	0 (0)	90.4	48	12
CRM+AR		0 (13)	.1 (1.5)	.3 (.3)	.1 (0)	0 (0)	98.9	49	9
11	1	(2, 5)	(4, 10)	(6, 15)	(20, 30)	(30, 20)
π01		.05	.10	.14	.24	.14
BIT-2d		.2 (3.4)	.6 (3.7)	1.3 (4.0)	6.5 (5.8)	.5 (3.2)
BIT-1d		0 (4.3)	.5 (5.5)	.8 (6.4)	4.9 (9.0)	.6 (4.0)
CRM+AR		.2 (4.3)	.3 (4.5)	.8 (5.0)	3.9 (6.9)	.9(6.9)
11	2	(5, 20)	(7, 40)	(8, 60)	(45, 50)	(55, 40)
π01		.19	.37	.55	.28	.18
BIT-2d		2.2 (4.5)	20.5 (9.7)	66.8 (20.1)	.7 (4.4)	0 (1.0)	.7	13	38
BIT-1d		3.6 (4.9)	27.8 (8.3)	60.4 (12.1)	1.2 (3.4)	0 (1.5)	.2	13	32
CRM+AR		2.2 (6.2)	21.2 (8.2)	69.0 (11)	1.3 (6.5)	.2 (6.5)	0	16	33
12	1	(1, 5)	(2, 25)	(3, 45)	(4, 65)	(5, 85)
π01		.05	.25	.44	.62	.81
BIT-2d		0 (3.0)	.3 (3.4)	5.1 (4.9)	26.5 (10.6)	65.8 (23.8)
BIT-1d		0 (3.1)	1.3 (3.7)	11.2 (5.5)	36.3 (8.4)	42.4 (9.2)
CRM+AR		0 (3.7)	.8 (5.1)	6.1 (6.5)	22.0 (7.7)	66.9 (7.7)
12	2	(5, 5)	(10, 28)	(20, 48)	(30, 65)	(40, 70)
π01		.05	.25	.38	.46	.42
BIT-2d		0 (3.0)	.4 (3.3)	1.4 (3.5)	.4 (3.0)	0 (1.4)	.1	8	60
BIT-1d		0 (3.7)	1.5 (8.1)	5.2 (9.9)	1.9 (5.0)	.2 (1.9)	0	11	49
CRM+AR		0 (4.3)	1.0 (5.6)	2.2 (7.2)	1.0 (5.9)	0 (5.9)	0	10	50

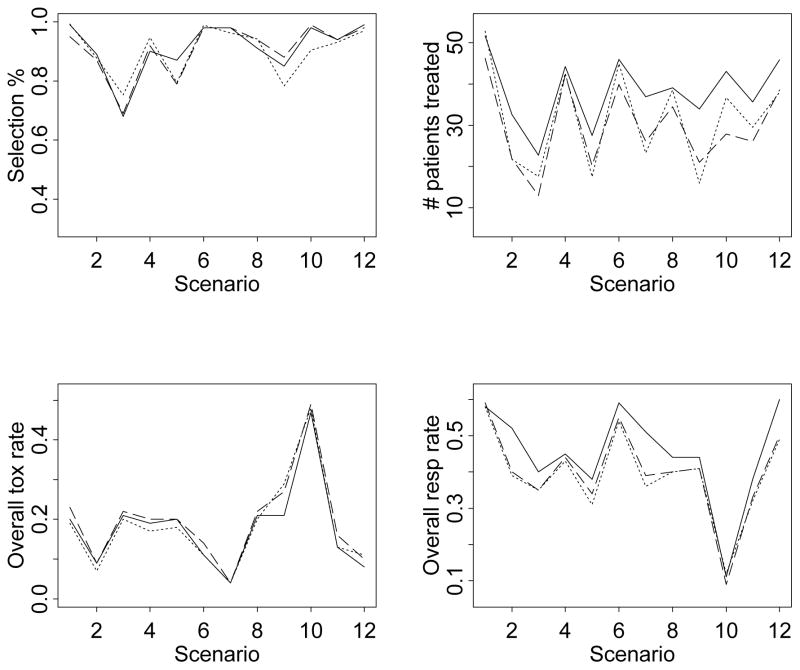
For ease of exposition, we provide summary plots of the main simulation results in Figure 2. Table 1 and Figure 2 suggest that the one-dimensional BIT design and the CRM + AR design both perform comparably to the two-dimensional BIT design in terms of the percentage of selecting the target dose-schedule combinations. The main advantage of the two-dimensional BIT design is that it assigns more patients to the target dose-schedule combinations than the other two methods. The one- and two-dimensional BIT designs are comparable in terms of the overall toxicity rates. Both designs yield slightly lower toxicity rates than the CRM + AR design. Finally, the two-dimensional BIT design has the highest overall response rates among all three designs.

Figure 2.

Summary operating characteristics based on the simulations: —— two-dimensional BIT design . . . . . . one-dimensional BIT design – – – CRM+AR design. The top two plots are the selection percentages of the target dose-schedule combinations and the numbers of patients treated (averaged across 1000 simulated trials) at these combinations. The bottom two plots are the overall observed toxicity and response rates, calculated by dividing the total numbers of patients who experienced toxicity and efficacy, respectively, by the total numbers of patients treated in the 1000 simulated trials.

We also evaluated the operating characteristics of three alternative designs. The first design used the model proposed by Yin et al. [5] (YLJ design) independently for each schedule (in a manner similar to the one-dimensional BIT design). The second and third designs were similar to the two stage CRM + AR design, in which we used either the CRM or the 3+3 algorithm [21] during the first stage while during the second stage we replaced the adaptive randomization with equal randomization at the MTDs. None of these designs performed as well as the one-dimensional, two-dimensional BIT design, or the CRM + AR design. Therefore, we did not include comparison results to these methods.

Because independence was assumed in our simulation scenarios, we performed additional simulations assuming different levels of (positive) correlation (odds ratio = 5 or 2.5) between the efficacy and toxicity outcomes in our simulation scenarios. The results from these simulations were not appreciably different from the results summarized above and are available from the first author upon request.

6 Discussion

We have proposed a Bayesian adaptive design for finding a desirable dose-schedule combination by jointly modeling binary toxicity and efficacy outcomes. To our knowledge, this is the first application of a Bayesian isotonic transformation (BIT) to the calculation of posterior distributions of partially-ordered toxicity probabilities in a dose-finding setting. The proposed two-dimensional BIT design performs better than the one-dimensional BIT design and the various two-stage designs we have explored.

Instead of performing an isotonic regression on samples drawn from the posterior distribution of the unconstrained toxicity probabilities, we implemented the isotonic transformation on the posterior means of the unconstrained toxicity probabilities and obtained considerably worse operating characteristics (results not shown). This suggests the advantage of transforming the draws from the unconstrained posterior density in small sample settings such as phase I/II oncology trials.

In applying our method, considerations should be given to the choice of the maximum sample size. In general the maximum number of patients in a dose-schedule-finding trial is a function of the number of doses and schedules examined. A rule of thumb in phase I studies is to use approximately six patients per dose studied (by which we arrived at 60 patients for the leukemia trial since we had 10 dose-schedule combinations). In addition, the operating characteristics achieved in our simulation studies further justified the use of this sample size. We recommend using the above rule of thumb as an initial guess in designing a dose-schedule-finding trial, and then further identifying an appropriate maximum sample size to achieve desirable operating characteristics via simulations, in conjunction with the calibration of the tuning parameters P_n, P_a and Q_a.

The proposed design can be directly applied to a two-agent trial where only two dose levels are under consideration for one of the agents. In this case, the model, algorithm, and matrix-order constraints can be used without modification. Although we assumed the same number of doses between schedules, the proposed design is also applicable to cases in which the number of doses between schedules is different. In addition, the proposed design is applicable to dose-finding trials in which both single and combination therapies are under investigation. For example, the investigator in an oncology trial may be interested in studying a range of chemotherapy doses with or without radiation therapy at a fixed dose. The goal of such a study is to determine the best combination of treatment options (i.e., dose of chemotherapy and radiation versus no radiation). The radiation therapy above can also be replaced with a second chemotherapy at a fixed dose. In these cases, the toxicity matrix ordering assumption across combinations of treatment options remains plausible, thus allowing the application of the proposed BIT design.

The proposed design can be extended to accommodate different order constraints than the matrix ordering among the toxicity and efficacy probabilities, such as increasing or umbrella ordering [22] for efficacy. In these cases, the minimum lower sets algorithm (MLSA) remains applicable, and the dose-schedule-finding algorithm can be modified accordingly.

Extension of the proposed design to trials with more than two schedules is straightforward. The MLSA can be implemented in a manner similar to the implementation described for the two-schedule case. Computational intensity will increase with the number of schedules. For example, when the number of schedules is three and the number of doses for each schedule is five, the maximum possible number of weighted averages to be calculated in each step of the MLSA is $\left(\begin{array}{c}3+5\\ 3\end{array}\right)-1=55$ [15]. Since in practice it is uncommon that the number of schedules under consideration exceeds 3, the efficiency of the proposed dose-schedule-finding algorithm is adequate.

As an alternative, one may model the toxicity and efficacy outcomes independently. Specifically, one could proceed by specifying independent beta priors for the toxicity and efficacy probabilities at each dose-schedule combination (hence resulting in beta posteriors) and order the posterior draws of the toxicity probabilities using the MLSA. This would reduce the complexity of the model considerably although it might potentially lead to less reliable estimates of the joint probabilities of toxicity and efficacy. Furthermore, under such an independence model, one would need to modify the proposed decision rules since rules 3–6 in our dose-schedule-finding algorithm depend on the joint posterior probabilities of toxicity and efficacy.

In our trial example, six cycles of treatment were administered under schedule 1 while two cycles of treatment were administered under schedule 2. Treating these as nested schedules, one can extend the dose-schedule-finding method of Braun et al. [7]. Specifically, one would need to model both toxicity and efficacy, and to find the best dose per treatment administration, the optimal number of treatment cycles, and the best qualitative schedule.

The decision rules in our design are based on posterior probabilities (computed using transformed posterior samples) which explicitly take into account the variability in the posterior distribution. Moreover, when performing the BIT, dose-schedule combinations with less information are assigned less weights. In exploring alternative decision rules, we found that our rules, which incorporate posterior probabilities, tend to perform better than those based solely on posterior means. Ivanova and Wang [13] proposed a practical and novel approach based on a bivariate isotonic regression of the toxicity estimates. While easier to implement, their decision rules do not take into account the variability in the parameter estimates. A potential area of future research would be to explore the utility of the simple bivariate isotonic regression in the context of dose-schedule finding. Such an implementation would require defining a suitable model and decision rules.

7 Appendices

1. An example of applying the minimum lower sets algorithm (MLSA)

We give a simplistic example of how the MLSA is carried out in obtaining the isotonically transformed sample μ̃^*.

Suppose doses 3 and 2 are the highest tried doses in schedules 1 and 2, respectively. We assume an untransformed sample μ̃ with weights w_jk as follows (taken from a similar simulation realization):

$$\begin{array}{l}{\stackrel{\sim }{\mu }}_{11}=-1.3(w_{11}=3/8),{\stackrel{\sim }{\mu }}_{12}=-1.2(w_{12}=1/8),{\stackrel{\sim }{\mu }}_{13}=-1.8(w_{13}=1/8),\\ {\stackrel{\sim }{\mu }}_{21}=-1.6(w_{21}=2/8),{\stackrel{\sim }{\mu }}_{22}=-1.4(w_{22}=1/8).\end{array}$$

These μ̃_jk correspond to the unordered toxicity probabilities p̃_jk as follows:

$$\begin{array}{l}{\stackrel{\sim }{p}}_{11}=.21,{\stackrel{\sim }{p}}_{12}=.23,{\stackrel{\sim }{p}}_{13}=.14,\\ {\stackrel{\sim }{p}}_{21}=.17,{\stackrel{\sim }{p}}_{22}=\mathrm{.20.}\end{array}$$

The partial order is violated between (p̃₁₁, p̃₁₂) and p̃₁₃, between p̃₁₁ and p̃₂₁, and between p̃₁₂ and p̃₂₂. The weights w_jk (as precisions) are positively correlated with the sample sizes at the corresponding dose-schedule combinations. That is, with a given toxicity probability, the larger the sample size, the larger the weight. To calculate μ̃^*, the MLSA proceeds as follows.

• Step 1: All possible nonempty lower sets can be found as {(1, 1)}, {(1, 1), (1, 2)}, {(1, 1), (1, 2), (1, 3)}, {(1, 1), (2, 1)}, {(1, 1), (1, 2), (2, 1)}, {(1, 1), (1, 2), (2, 1), (2, 2)}, {(1, 1), (1, 2), (1, 3), (2, 1)}, and {(1, 1), (1, 2), (1, 3), (2, 1), (2, 2)}. For definitions of lower and level sets, see [15]. Also, contact the first author for the closed-form expressions of the nonempty lower sets in the matrix ordering case.

  The MLSA computes the weighted average of the μ̃_jk’s on each of the above lower sets and finds the minimum average value, which is −1.44, and the corresponding lower set (also level set) of the largest size, which is {(1, 1), (1, 2), (1, 3), (2, 1)}. Hence we obtain ${\stackrel{\sim }{\mu }}_{11}^{\ast }={\stackrel{\sim }{\mu }}_{12}^{\ast }={\stackrel{\sim }{\mu }}_{13}^{\ast }={\stackrel{\sim }{\mu }}_{21}^{\ast }=-1.44$.

• Step 2: Consider all the nonempty level sets of the form L ∩{(1, 1), (1, 2), (1, 3), (2, 1)}^c, where L is any nonempty lower set (listed in Step 1), i.e., level sets consisting of lower sets with {(1, 1), (1, 2), (1, 3), (2, 1)} subtracted. There is only one such level set, which is {(2, 2)}. The minimum weighted average, which is simply the weighted average of μ̃_jk on the level set {(2, 2)}, is μ̃₂₂ = −1.4. Hence we have ${\stackrel{\sim }{\mu }}_{22}^{\ast }=-1.4$.

The isotonically transformed μ̃^* thus is

$$\begin{array}{l}{\stackrel{\sim }{\mu }}_{11}^{\ast }=-1.44,{\stackrel{\sim }{\mu }}_{12}^{\ast }=-1.44,{\stackrel{\sim }{\mu }}_{13}^{\ast }=-1.44,\\ {\stackrel{\sim }{\mu }}_{21}^{\ast }=-1.44,{\stackrel{\sim }{\mu }}_{22}^{\ast }=-1.4;\end{array}$$

and the corresponding toxicity probabilities that satisfy the specified partial order constraints, denoted as ${\stackrel{\sim }{p}}_{jk}^{\ast }$, are

$$\begin{array}{l}{\stackrel{\sim }{p}}_{11}^{\ast }=.19,{\stackrel{\sim }{p}}_{12}^{\ast }=.19,{\stackrel{\sim }{p}}_{13}^{\ast }=.19,\\ {\stackrel{\sim }{p}}_{21}^{\ast }=.19,{\stackrel{\sim }{p}}_{22}^{\ast }=\mathrm{.20.}\end{array}$$

2. Computational aspects

Computing

Suppose ${\stackrel{\sim }{\mathit{\mu }}}_{jk}^{(1)},\dots ,{\stackrel{\sim }{\mathit{\mu }}}_{jk}^{(M)}$ are M thinned, unconstrained posterior samples of μ_jk from the Gibbs sampler. Then each weight w_jk (required to calculate the weighted average of μ_jk) as the inverse variance of the samples ${\stackrel{\sim }{\mathit{\mu }}}_{jk}^{(1)},\dots ,{\stackrel{\sim }{\mathit{\mu }}}_{jk}^{(M)}$ is computed only once. Given the weights w_jk, the calculation of the weighted average is simple arithmetic and the amount of calculation depends mainly on the number of μ_jk belonging to a level set, which is always a subset of the largest possible lower set. In fact, one can derive a formula for the upper bound of the size of the largest possible lower set (not shown). In particular, when two schedules and five doses under each schedule are under investigation, at most 20 weighted averages are to be calculated in each step of the MLSA. Furthermore, such calculation will be reduced considerably and adaptively while the trial proceeds because of the reduced sizes of the level sets. In sum, calculations using the MLSA in dose-schedule-finding settings compare favorably in efficiency with other general algorithms given in [15].

Programming

Due to the relatively simple form of the lower and level sets (not shown), the programming of the MLSA is straightforward. A C++ function for this algorithm is available from the first author upon request. We are also in the process of making R code available.

3. Details of the one-dimensional BIT design

In the one-dimensional BIT design, we start a phase I/II trial under schedule 1 assuming a maximum of 30 patients will be enrolled at this schedule. We apply the Bayesian isotonic transformation approach in which we order-transform the unconstrained posterior MCMC draws of the toxicity probabilities using the PAVA. We use the PAVA because of the simple toxicity probability ordering. Dose assignments follow the same principles in the two-dimensional BIT design, modified to allow only within-schedule dose escalation. Once a maximum of 30 patients have been evaluated under schedule 1, we choose a target dose under this schedule that has the largest posterior probability of {p ≤ .3, q ≥ .3} and then begin enrolling a maximum of (60 - the number treated under schedule 1) patients under schedule 2. Once all patients have been evaluated under schedule 2, we select a target dose that has the largest posterior probability of {p ≤ .3, q ≥ .3}. For this dose-schedule-finding design, there are three possibilities for selecting target doses under the two schedules: 1) No target dose is selected for either schedule. In this case we will not select a final dose-schedule combination; 2) Only one target dose is selected. Then this dose-schedule combination is selected as the final dose-schedule combination; 3) For each schedule, one target dose is selected. In this case the dose-schedule combination with a larger posterior probability of {p ≤ .3, q ≥ .3} (out of the two selected) is chosen as the final dose-schedule combination. In those rare cases when the two selected doses have the same posterior probability of {p ≤ .3, q ≥ .3}, we select the dose under schedule 1 as the final dose-schedule combination (alternatively, one could also select the other combination or randomly select from these two).

4. Details of the CRM + AR design

In the CRM + AR design a total of 60 patients will be allocated to dose-schedule combinations in order to find the best combination. In the first stage of the design, we employ the CRM under each schedule to locate the within-schedule MTD. We set a maximum number of 18 patients per schedule for the CRM in the first stage.

For the CRM, the model parameters within the kth schedule are (p̂_1k, …, p̂_Dk, α) such that the probability of toxicity at dose level j under schedule k equal to ${\widehat{p}}_{jk}^{\alpha }$. Each p̂_jk is fixed with 0 < p̂_1k < p̂_2k <···< p̂_Dk < 1, and α a priori follows an exponential distribution with mean 1. For the simulations described in Section 5, we use (p̂_1k, p̂_2k, …, p̂_Dk) = (0.05, 0.15, 0.20, 0.30, 0.45), k = 1, 2. The CRM proceeds by sequentially selecting a dose under a given schedule that minimizes | $E({\widehat{p}}_{jk}^{\alpha }\mid \text{Data})-\overline{p}$|. To ensure a fair comparison, we use a version of the CRM which stops early for excessive toxicity within a schedule, since our proposed method can stop at anytime due to excessive toxicity. The additional rule is to terminate the trial if $Pr({\widehat{p}}_{1k}^{\alpha }>\overline{p}\mid \text{Data})>0.95$. Note that it is possible that two MTDs are selected, only one MTD is selected (in cases where the CRM indicates that all doses under a particular schedule are overly toxic), or no MTD is selected (in cases where the CRM indicates that all doses under both schedules are overly toxic). When no MTD is selected in the first stage, the trial is terminated. Below, we assume an MTD is selected for at least one schedule.

Denote n₁ the total number of patients allocated to both schedules by the CRM. After the MTDs under both schedules have been selected, in the second stage we adaptively randomize the remaining (60 − n₁) patients to the set of doses at or below the MTDs. Based on a simple model to be described below, we use the probability ${AR}_{jk}^{\ast }=Pr(p_{jk}\le \overline{p},q_{jk}\ge \underset{\_}{q}\mid \text{Data})$ for adaptive randomization, such that the next patient to enroll in the trial during the second stage is assigned to the jth dose and kth schedule with probability

$$A{R}_{jk}=\frac{{AR}_{jk}^{\ast }}{{\displaystyle \sum _{jk}}{AR}_{jk}^{\ast }}.$$

The above posterior probability is computed under a simple Bayesian model, which we now describe. Using the notation introduced in this paper, we assume that the joint toxicity and efficacy response at any dose-schedule combination (j, k) follows a multinomial distribution, which leads to the same likelihood function given by (3). In addition, we assume that the joint probabilities of toxicity and efficacy, given in the vector ${\pi }^{(jk)}=({\pi }_{00}^{(jk)},{\pi }_{01}^{(jk)},{\pi }_{10}^{(jk)},{\pi }_{11}^{(jk)})$, follows a vague Dirichlet prior Dir(.25, .25, .25, .25). Under the multinomial likelihood function (3), the posterior of π^(jk) is also a Dirichlet. Then the AR probability above can be easily computed using this Dirchlet posterior since $p_{jk}={\pi }_{10}^{(jk)}+{\pi }_{11}^{(jk)}$ and $q_{jk}={\pi }_{01}^{(jk)}+{\pi }_{11}^{(jk)}$.

In addition to the adaptive randomization scheme described above, efficacy is monitored according to the probability rule: P(q_jk < q | Data) > 0.95, where q = 0.3 is the target efficacy probability. Similarly, toxicity is monitored according to the probability statement: P(p_jk > p̄ | Data) > 0.95 where p̄ = 0.3 is the target toxicity probability. Specifically, if at any point during the course of the trial either of the above two inequalities is satisfied, patients will no longer be randomized to that dose-schedule combination. At the end of the trial the dose with the largest Pr(p_jk ≤ p̄, q_jk ≥ q| Data) is selected as the recommended dose-schedule combination.