A model for attentional information routing through coherence predicts biased competition and multistable perception

Abstract

Selective attention allows to focus on relevant information and to ignore distracting features of a visual scene. These principles of information processing are reflected in response properties of neurons in visual area V4: if a neuron is presented with two stimuli in its receptive field, and one is attended, it responds as if the nonattended stimulus was absent (biased competition). In addition, when the luminance of the two stimuli is temporally and independently varied, local field potentials are correlated with the modulation of the attended stimulus and not, or much less, correlated with the nonattended stimulus (information routing). To explain these results in one coherent framework, we present a two-layer spiking cortical network model with distance-dependent lateral connectivity and converging feed-forward connections. With oscillations arising inherently from the network structure, our model reproduces both experimental observations. Hereby, lateral interactions and shifts of relative phases between sending and receiving layers (communication through coherence) are identified as the main mechanisms underlying both biased competition as well as selective routing. Exploring the parameter space, we show that the effects are robust and prevalent over a broad range of parameters. In addition, we identify the strength of lateral inhibition in the first model layer as crucial for determining the working regime of the system: increasing lateral inhibition allows a transition from a network configuration with mixed representations to one with bistable representations of the competing stimuli. The latter is discussed as a possible neural correlate of multistable perception phenomena such as binocular rivalry.

it is a widespread belief that the brain has limited resources available for information processing (Marois and Ivanoff 2005). Selective attention provides a means of efficient and flexible operation under this restriction by allowing preferential allocation of processing resources to a particular area or feature in the visual scenery while ignoring distractors.

Hints towards the mechanisms selective attention employs are provided by two seminal studies. By showing a preferred and a nonpreferred stimulus at separate spatial locations to a V4 neuron, Moran and Desimone (1985) discovered that presenting both at the same time results in an averaged rate between the rates the stimuli would elicit if presented alone. Attending one stimulus biased the response towards the rate the attended stimulus would evoke if presented alone (biased competition). These results suggest that attention selectively modulates the information flow through the visual hierarchy. Grothe et al. (2015) tested this hypothesis directly for the first time: by independently varying the luminance of two stimuli eliciting equally strong responses in V4 neurons, it was found that the luminance modulation of the attended stimulus was represented in the neuronal activity, but the modulation of the nonattended stimulus, however, was represented to a much lesser degree.

Fries (2005) proposed a possible mechanistic explanation for these effects by introducing the concept of “Communication through Coherence” (CTC): a neuron with oscillating membrane potential can be driven to fire by relatively weak input when it is close to the threshold, while if it is in a phase of low excitability, even stronger input might fail to elicit an action potential. Thus shifting relative phases of oscillating sending and receiving populations could be utilized to gate information. Experimental support is provided by the findings that attention increases synchrony of γ-oscillations within V4 (Taylor et al. 2005; Fries et al. 2001, 2008), that communication between different populations oscillating in the γ-band is most effective for a specific phase relation (Womelsdorf et al. 2007), and that the γ-coherence between neuronal ensembles in V1 and V4 is elevated under attention (Grothe et al. 2012; Bosman et al. 2012). Also, Gregoriou et al. (2009) showed that CTC might be used for effective communication between the frontal eye field and V4.

Several models were conceived that exploit oscillatory dynamics to explain information routing or biased competition (Masuda 2009; Akam and Kullmann 2010; Boergers and Kopell 2008; Boergers et al. 2008; Tiesinga and Sejnowski 2010; Wildie and Shanahan 2012; Zeitler et al. 2008; Montijn et al. 2012; Mishra et al. 2006). However, there is no model that has been shown to reproduce both key experimental findings in a unifying framework while implementing a phase-shifting mechanism in a biologically plausible manner. We hypothesize that feed-forward networks of recurrently coupled, mixed excitatory and inhibitory neurons with distance-dependent lateral interaction are capable of achieving just that.

By constructing a two-layered, fan-in feed-forward system with lateral connectivity, mimicking the convergent architecture of the visual system, we show that intrinsically generated oscillations “self-organize” their relative phase relations to optimize information transmission for attended stimuli. This enables our model to reproduce both biased competition and information routing. We query the robustness of our finding and confirm that both effects are observed over a broad range of relevant model parameters. Furthermore, we identify different working regimes of the model, enabling both mixed and bistable representations of the competing stimuli, which establishes a link to the occurrence of multistable perception phenomena, such as binocular rivalry.

MATERIALS AND METHODS

Neuron and synapse model.

We modeled both excitatory and inhibitory neurons as quadratic integrate and fire units with a membrane potential described by

$$C_{\text{m}}\dot{V}=p_{\text{2}}{V}^{\text{2}}+p_{\text{1}}V+p_{\text{0}}+g_{\text{e}}\left(V-V_{\text{e}}\right)+g_{\text{i}}\left(V-V_{\text{i}}\right),$$ (1)

where the membrane capacitance C_m is calculated as

$${\mathit{\text{C}}}_{\mathit{\text{m}}}=\text{1}\frac{\mu \text{F}}{{\text{cm}}^{\text{2}}}\cdot \mathit{\text{A}}.$$ (2)

A denotes the surface area of the neuron. The surface of excitatory neurons (A_e) is bigger than the surface of inhibitory ones (A_i). Numerical values for A_e and A_i are in accordance with Pospischil et al. (2008). The dynamic equation for excitatory and inhibitory neurons only differs in the value of C_m. The parameters p_0,1,2 were found by mathematical reduction of a Hodgkin-Huxley type model (Abbott and Kepler 1990) similar to the one used by Bartos et al. (2002) to model inhibitory neurons generating γ-rhythms in cortex. The variable g_e (g_i) is the excitatory (inhibitory) conductance with respective reversal potential V_e (V_i), governed by

$$g_{\mathrm{e}}\left(t\right)={\omega }_{\mathrm{e}}{\displaystyle \sum _{\mathit{\text{s}}=1}^{n_{\mathrm{e}}}\mathrm{\Theta }\left(t-t_{\text{s},\mathrm{e}}-d\right)\exp \left(\frac{-\left(t-t_{\text{s},\mathrm{e}}-d\right)}{{\tau }_{\mathrm{e}}}\right)}$$ (3)

$$g_{\text{i}}\left(t\right)={\omega }_{\text{i}}{\displaystyle \sum _{s=1}^{n_{\text{i}}}\mathrm{\Theta }\left(\text{t}-t_{\text{s},\text{i}}-d\right)\left[{\chi }_1\hspace{0.17em}\exp \left(\frac{-\left(t-t_{\text{s},\text{i}}-d\right)}{{\tau }_{\text{i}}^1}\right)+{\chi }_{\text{2}}\hspace{0.17em}\exp \left(\frac{-(t-t_{\text{s},\text{i}}-d)}{{\tau }_{\text{i}}^{\text{2}}}\right)\right]}\hspace{0.17em}\cdot$$ (4)

Here, t_s,e denote the times of presynaptic excitatory spikes and t_s,i the times of inhibitory ones. Θ Is the Heaviside function. The synaptic delay is symbolized by d. Furthermore, in accordance with Bartos et al. (2002), the synaptic weight ω_i of inhibitory connections is generally taken to be stronger than the weight ω_e of excitatory synapses and the response to an inhibitory spike has a fast and a slow component, where relative contributions are controlled by χ_1,2 with χ₁ + χ₂ = 1. The absolute values of ω_e and ω_i were chosen such that the network is in an oscillatory activity regime under stimulation. If the membrane potential crosses V_θ, a spike is generated and the potential set back to V_reset. The model parameters and their default values can be found in Table 1. If not stated otherwise, the default values were used.

Table 1.

Model parameters

Variable	Ae	Ai	p0	p1	p2
(Default) value	2.88 × 10−4 cm2	1.2 × 10−4 cm2	3.90 × 10−9 A	1.30 × 10−7 $\frac{\text{A}}{\text{V}}$	1.08 × 10−6 $\frac{\text{A}}{{\text{V}}^2}$
Variable	Vθ	Vreset	τe	τi1	τi2
(Default) value	−56.23 mV	−67.00 mV	3 ms	1.2 ms	8 ms
Variable	χ1	χ2	Ve	Vi	ωe
(Default) value	0.9	0.1	0 mV	−75 mV	0.4 nS
Variable	ωi	plocie	plocii	pAC	μ
(Default) value	1.2 nS	0.2	0.2	0.1125	0.5
Variable	pABei	pCDie	pCDii
(Default) value	0.08	0.10	0.10

If not stated otherwise, the default values were used.

A_e,i, surface area of excitatory, respectively, inhibitory neurons; p_0,1,2, parameters of the quadratic integrate- and-fire model; V_θ, firing threshold; V_reset, reset potential; τ_e, excitatory synaptic time constant; τ_i^1,2, inhibitory synaptic time constants; χ_1,2, relative contribution of fast and slow inhibitory components to the joint inhibitory response. V_e,i, excitatory respectively inhibitory reversal potential; ω_e,i, excitatory respectively inhibitory synaptic weight; p_loc^ie, connection probability from inhibitory to excitatory neurons in a local population; p_locⁱⁱ, connection probability between inhibitory neurons in a local population; p_AC, connection probability from excitatory neurons in local population A to all neurons in local population C; μ, cross-talk parameter (p_BC = μ · p_AC); p_AB^ei, connection probability from excitatory neurons in A to inhibitory neurons in B and vice versa; p_CD^ie, connection probability from inhibitory neurons in C to excitatory neurons in D and vice versa; p_CDⁱⁱ, connection probability between inhibitory neurons in C and D.

Local structure.

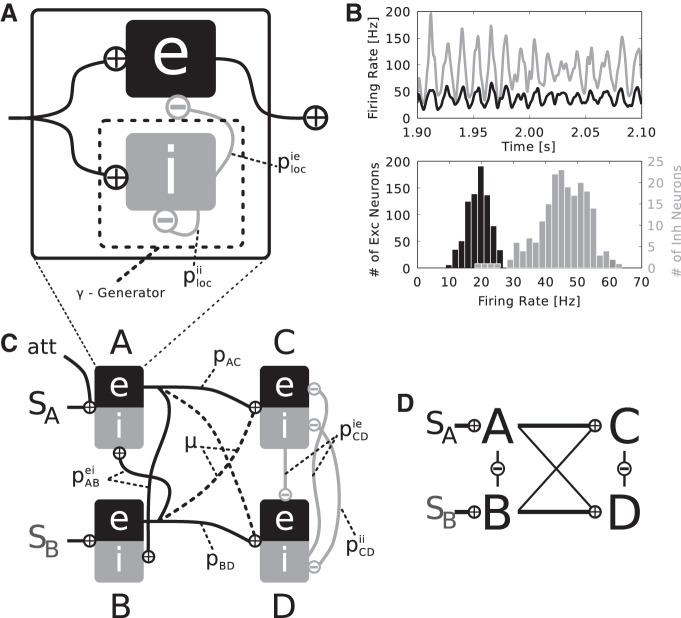
Local populations were formed as recurrent networks of 800 excitatory and 200 inhibitory neurons [ratio of 4:1 (Beaulieu et al. 1992)] with sparse connectivity probabilities p_loc^ie and p_locⁱⁱ, i.e., recurrent connections only exist within the inhibitory population and from the inhibitory to the excitatory population. We assume that the neurons making up a local population represent a patch of visual cortex that is activated by a circular stimulus of 1° diameter. Assuming retinotopy and a cortical magnification factor of 1°/mm (Albus 1975; Tusa et al. 1978), this translates to a stimulated cortical area of 1-mm diameter. All recurrent connections within the local population are inhibitory, which were found to have a conduction speed of ∼0.1 m/s (Salin and Prince 1996). Thus we would expect conduction delays to range from 0 to 10 ms. For simplicity we set all delays d to the mean of 5 ms. Figure 1A shows a schematic drawing of the basic local circuitry.

Fig. 1.

Local and global network setup. A: a local population consists of externally driven, recurrently coupled 800 excitatory and 200 inhibitory neurons. Recurrent synapses in the inhibitory subpopulation, instantiated with coupling probability p_locⁱⁱ, generate a γ-rhythm. This rhythm is imposed onto the excitatory subpopulation via connections from the inhibitory to the excitatory subpopulation with probability p_loc^ie. B: such a local population generates a stable γ-population-rhythm, as seen in the exemplary time courses of activity of the inhibitory (gray) and excitatory (black) subpopulation (top). Inhibitory neurons fire at markedly higher rates than their excitatory counterparts, as shown in the mean firing rate histogram (bottom). C: 4 local populations are interconnected to form the 2-layered global setup. The 1st layer populations A and B are driven by Poissonian spike trains representing 2 different stimuli S_A and S_B. Both 1st layer populations project to both 2nd layer populations C and D, whereas A and C, respectively B and D, are connected with the same coupling probability p_AC = p_BD. The strength of cross talk between A and D, respectively B and C, is regulated by the mixing parameter μ, i.e., p_AD = p_BC = μ·p_AC with μ $\in$ [0,1]. The value of μ determines the relative preference of S_A and S_B to C and D, i.e., if 0 < μ < 1, S_B (S_A) will be a nonpreferred stimulus for C (D). Intralayer lateral interactions differ between the 2 layers and depend on connection probabilities p_AB^ei, p_CD^ie, and p_CDⁱⁱ. In the 2nd layer, populations C and D are assumed to act as similar computational units due to the partly overlapping receptive fields, thus the lateral connectivity is the same as within local populations (see A) at lower strength (p_CD^ie < p_loc^ie and p_CDⁱⁱ < p_locⁱⁱ). Attention is introduced as an additional input to 1 1st layer population (here A). All coupling probabilities and model parameters can be found in Table 1. D: simplified layout diagram of the full setup depicted in C used in Fig. 2.

Input to the population is delivered via afferent connections that impinge onto both excitatory and inhibitory neurons (Zemankovics et al. 2013; Haeusler and Maass 2007; Lee et al. 2014). This setup can be seen as an extended implementation of the dynamical network motif of feed-forward inhibition, which is frequently encountered in local cortical, cotico-cortical, and thalamo-cortical cicuits (Womelsdorf et al. 2014). The most stripped down version of this motif only has an inhibitory connection onto the excitatory subpopulation and common input driving both excitatory and inhibitory subpopulations. The functional interpretation is that potential oscillations in the input stream are selectively extracted: The inhibitory subpopulation resonates with the input oscillation, and, with a certain conduction delay, rhythmically inhibits the excitatory subpopulation. Since the excitatory subpopulation receives the same input as the inhibitory one at the same time, but is inhibited with a delay, the peak that causes the inhibitory population spike is passed through the excitatory subpopulation. Thus such circuitry is prone to selectively gate oscillatory input in a certain frequency range, depending on neuronal time constants and the delay of local inhibition. Our implementation is extended in the sense that the inhibitory subpopulation generates a local γ-oscillation via recurrent inhibition, which is imposed onto the excitatory population, even in the absence of oscillations in the input. The design of this inhibitory subnetwork stems from a model of γ-generating circuits in the cortex by Bartos et al. (2002).

Figure 1B shows example mean firing rate traces and rate distributions of the excitatory and inhibitory subpopulation when driven by 135 independent Poissonian spike trains, each at a rate of 13 Hz, revealing stable γ-oscillations. Whereas most inhibitory neurons fire slightly below the population frequency of the network, the excitatory neurons fire typically at markedly lower rates, as observed in electrophysiological studies (Csicsvari et al. 1998, 1999; Kerlin et al. 2010; Hofer et al. 2011; Vinck et al. 2013; Constantinidis et al. 2002; Mitchell et al. 2007).

Global structure.

To emulate the converging feed-forward characteristic of the visual system, we arrange four local populations A, B, C, and D in two layers. In the first layer, populations A and B are driven by stimuli S_A and S_B. The excitatory subpopulations of A (A_exc) and B (B_exc) project to C and D in the second layer. Pairs AC and BD are connected by equal probabilities p_AC = p_BD, where as the strength of crosstalk between pairs AD and BC is determined by p_AD = p_BC = μ·p_AC, with μ $\in$ [0, 1]. The mixing variable μ controls the relative preference of the stimuli to the populations in the second layer. The fact that in the first layer the populations are driven directly only by one stimulus, but by both in the second layer, reflects the growth of receptive field sizes along the visual stream (Kretzberg and Ernst 2013).

We implement lateral interaction within the layers as structured according to the tuning properties of populations. Feature-specific lateral coupling has been proposed to account for various computational effects, for example, iso-feature suppression in V1 (Li 2005) or contrast invariance of tuning curves (Ben Yishai et al. 1995). For a variety of features, specificity of lateral connections in visual cortex has been confirmed, showing that columns with similar tuning properties are more likely to be interconnected (Bosking et al. 1997; Chisum and Fitzpatrick 2004; Malach et al. 1993).

We presume the same to hold true when the feature is visual space and the tuning curve is usually called the receptive field. Hence, lateral coupling between populations with overlapping receptive fields should be different from lateral coupling between populations with nonoverlapping receptive fields, following the reasoning of Deco and Rolls (2005), who used as similar model setup to study biased competition with spiking neurons in the absence of oscillations. In that manner, we assume that between A and B with nonoverlapping classical receptive fields, lateral interaction is mediated by cross coupling from excitatory to inhibitory subpopulations. Lateral interaction in the second layer, where receptive fields overlap, is implemented by coupling the inhibitory subpopulation of C to the inhibitory and excitatory subpopulations of D and vice versa.

We make this particular choice for two reasons. Firstly, the lateral coupling between populations C and D is similar to the coupling within a local population (compare Fig. 1A), albeit at lower strength, which is consistent with assuming that populations with overlapping receptive fields become closer to act as one single rather than two separate computational units. On the other hand, populations A and B process different stimuli and can be interpreted as two separate computational units. Thus the lateral coupling between A and B is different to the coupling within a local population. Secondly, if the layers in the model are retinotopically organized, the distance-dependent lateral interaction in visual space translates to distance-dependent interaction in cortical space. The connectivity scheme we propose is then in line with the finding that in early visual cortex lateral connections reaching beyond the local column are usually mediated by excitatory neurons (Rockland and Lund 1983), whereas inhibitory projections are confined to the same or neighboring columns (Helmstaedter et al. 2009).

The delay d of the lateral synapses between C and D is also set to 5 ms, consistent with the assumption that both populations are in close vicinity and act similar to one population. In the first layer, we assume that A and B are populations directly adjacent in cortical space, thus processing different stimuli in their classical receptive field while lying in each others suppressive surround. Following the same reasoning as above, the mean distance between neurons in both populations is ∼1 mm. With a higher conductance speed of pyramidal axons, which we set to 0.2 m/s (Murakoshi et al. 1993; Nelson and Katz 1995; Hirsch and Gilbert 1991), this distance also translates to a delay of 5 ms.

The difference in the implementation of the lateral connectivity results in a differential effect on the phase relation between the populations in the first and second layer. In the second layer, C_exc and D_exc will tend to oscillate in phase, since the lateral coupling is conceived as similar to the coupling within each local population. In the first layer however, A_exc and B_exc will tend to oscillate in anti-phase. This can intuitively be understood by considering A_exc and B_exc as mutually inhibiting oscillators, where A_inh and B_inh merely serve to convert the excitatory output of A_exc and B_exc to inhibitory signals and add an additional time delay. The traveling time of the inhibitory signals between A_exc and B_exc is ∼14.2 ms (5 ms from A_exc to B_inh + 5 ms from B_inh to B_exc and vice versa). In addition to this, there is also the rise time of inhibitory (1.2 ms) and excitatory (3 ms) conductances. Roughly speaking, if the traveling time of the signal is close to the period of the oscillation T, A_exc and B_exc will tend to push each other out of phase, since this is the configuration in which the impact of the mutual inhibition is lowest. More precisely, the anti-phase steady-state solution of two inhibitory pulse coupled oscillators is stable for delays approximately in the interval from $\frac{3}{4}\text{T}$ to $\frac{5}{4}\text{T}$ (Klinshov and Nekorkin 2011). This situation is given with populations A and B oscillating at ∼70 Hz, resulting in a period T of ∼14 ms.

The layer-specific lateral connectivities also lead to distinctive effects on the mean firing rate. If populations A and B are both active, they will suppress each other, since the lateral coupling from excitatory to inhibitory subpopulations increases the overall inhibition in the layer. Thus A and B can be interpreted as acting as each others suppressive surround. In the second layer, populations C and D do not have a strong mutual suppressive effect. The lateral coupling mainly synchronizes C_inh and D_inh and overall inhibition remains largely unchanged.

Figure 1C shows the global setup of the model and Fig. 1D shows a simplified layout diagram used in following figures. The values of the connection parameters can be found in Table 1.

Stimuli.

The first layer populations A and B are driven by different input stimuli S_A and S_B. These stimuli are modeled as firing rates from which Poissonian spike trains are drawn. Every neuron (excitatory and inhibitory) in A and B receives 135 input synapses, which each transmit a Poissonian spike train at a mean rate of 13 Hz. Around the mean, the firing rates of S_A and S_B are independently modulated by a uniformly distributed random process with an amplitude of 2 Hz, where every 10 ms a new value is drawn. This models the effect of the luminance “flicker” signal used in the study of Grothe et al. (2015).

Attention.

In accordance with many experimental studies showing that directing attention towards a stimulus leads to a moderate increase in firing rate in early visual neurons driven by that stimulus (e.g., Chalk et al. 2010; McAlonan et al. 2008; Thiele et al. 2009; Herrero et al. 2008), attention is manifested as a supplementary input to both excitatory and inhibitory subpopulations in the respective local population (A or B) that processes the attended stimulus. More specifically, the supplementary input raises the mean rate of the Poisson process representing the attended stimulus by 1 to 14 Hz.

Simulation and analysis.

We simulated neural activity of networks in epochs of 2.4 s with a time step of 0.1 ms. The simulations were realized in the framework of the BRIAN neural network simulator (V1.4.1, http://briansimulator.org/; RRID:nif-0000-30223) (Goodman and Brette 2009). Every simulation for each set of parameters was performed 50 times with randomized initial conditions.

When we consider rates of neurons in response to a stimulus, we refer to the firing rates averaged over time, trials, and neurons within excitatory subpopulations.

To quantify the biased competition effect, we introduce two different scores. The intermediate response factor quantifies the relation of the rate at which neurons fire when both stimuli are present (r_b) to the rate observed when only the preferred (r_p) or the nonpreferred (r_np) stimulus is present as

$$\frac{r_{\text{b}}-r_{\text{np}}}{r_{\text{p}}-r_{\text{np}}}\cdot$$ (5)

A value of 0.5 thus describes the situation when the response to both stimuli is exactly between the two rates elicited by the preferred respectively nonpreferred stimulus alone. Here, information about both stimuli is represented to the same degree in the firing rate, concurrent with the biased competition effect.

The biased competition score indicates the effectiveness of rate recovery under attention. We consider the cases of “attend preferred” and “attend nonpreferred” separately. In the former case, the biased competition score is defined as

$$\frac{r_{\text{b}}^{\text{att p}}-r_{\text{b}}}{r_{\text{p}}-r_{\text{b}}},$$ (6)

in the latter case it is

$$\frac{r_{\text{b}}^{\text{att np}}-r_{\text{b}}}{r_{\text{np}}-r_{\text{b}}},$$ (7)

where r_b^{att p} (r_b^{att np}) is the rate when both stimuli are present and the preferred (nonpreferred) is attended. For perfect rate recovery, we would observe a value of 1 and 0 if attention had no effect at all on the rates.

To investigate the phase relation between two neuronal populations or subpopulations, we want to construct a measure that is 0 if both populations are in-phase and π/−π if they are in anti-phase. Due to the conduction delays in the network and a phase lag between membrane current and population spikes, it is not feasible to directly compare the population rates. Instead, we first compute the instantaneous phase ϕ_s(t) of the mean incoming current c_s(t) from all sending neurons via the analytic signal c_s^a(t):

$$c_{\text{s}}^{\text{a}}\left(t\right)=F^{-1}[F\text{(}{c}_{\text{s}}\text{(}t\text{))}\cdot 2\text{Θ}\left(\text{2π}f)\right]=c_{\text{s}}\text{(}t\text{)}+i\cdot H\text{(}{c}_{\text{s}}\text{(}t\text{)),}$$ (8)

where i is the imaginary unit, $F$ denotes the Fourier transform, and $H$ the Hilbert transform. Θ Is the Heaviside function and f symbolizes frequency. The phase ϕ_s(t) of c_s(t) is then the angle of the complex number c_s(t) + i·$H$[c_s(t)]. In the same way, we calculate the instantaneous phase ϕ_r(t) of the mean total incoming current c_r(t) to all receiving neurons. The phase difference Δϕ(t) is taken as the minimal difference of ϕ_s(t) and ϕ_r(t), i.e.

$$\Delta \varphi (t)=\arg \left[{\varphi }_{\mathit{\Upsilon }}(t)-{\varphi }_{\text{s}}(t)\right]$$ (9)

resulting in Δϕ $\in$ [−π, +π). In the course of this paper we only consider phase differences between excitatory subpopulations. As an example, a phase difference Δϕ of 0 between A and C means that the peaks of the mean current to C_exc originating from A_exc coincide with the peaks of the total mean current flowing into C_exc (i.e., the sum of the mean currents to C_exc originating from A_exc, B_exc, C_inh, and D_inh). In the same way, a phase difference Δϕ of π/−π occurs when the current peaks from A_exc coincide with the troughs of the total incoming current to C_exc.

The spectral coherence is a measure that was used to quantify information transmission between luminance signals and the activity of neurons in V4 by Grothe et al. (2015). For two signals x(t) and y(t) it is defined as

$${\text{SC}}_{xy}(f,\tau )=\left|{\displaystyle \sum _k{C}_{xy}^k(f,\tau )}\right|,$$ (10)

with

$$C_{xy}(f,\hspace{0.17em}\tau )\hspace{0.17em}=\frac{{\mathrm{\Sigma }}_i{W}_x^{*}(f,\hspace{0.17em}{t}_i)\hspace{0.17em}{W}_y(f,\hspace{0.17em}{\mathit{t}}_i+\hspace{0.17em}\tau )}{{\mathrm{\Sigma }}_i\left|W_{\mathit{x}}(f,\hspace{0.17em}{t}_i)\right|\hspace{0.17em}{\mathrm{\Sigma }}_i\left|W_y(f,\hspace{0.17em}{t}_i+\hspace{0.17em}\tau )\right|}\mathrm{.}\hspace{0.17em}$$ (11)

Here, W denotes the wavelet transform (the Morlet mother wavelet was used with width parameter 6), f symbolizes frequency, τ a time delay, i the time index, and k the trial index. We collapse the spectral coherence to a single spectral coherence score, independent of f and τ, by taking the mean over the full frequency spectrum and a set of τ for every frequency f. The width of this region of interest of τ (see nonhatched area in Fig. 6A) as a function of f is $\frac{6}{f}$. The center of the region is found ad hoc by taking the mean of the maxima of SC(f, τ) $\forall f\in$ [25 Hz, 65 Hz] and is the same for all frequencies f.

Fig. 6.

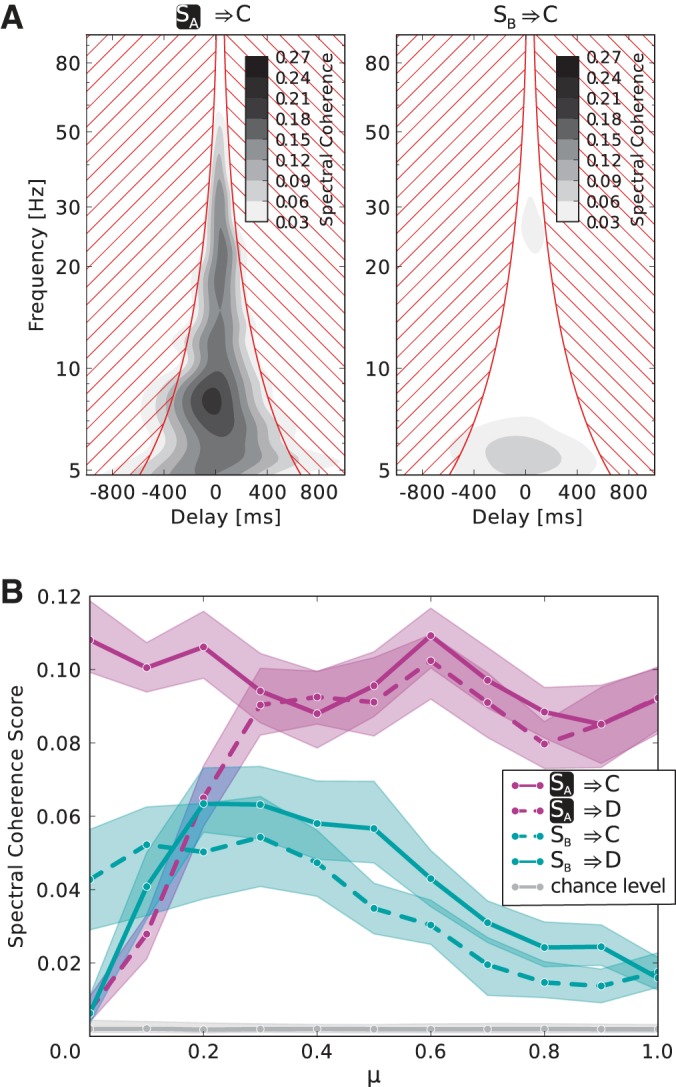
Information routing effect for different values of the mixing parameter μ. A: example of the full spectral coherence for the case that both stimuli are present and S_A is attended (μ = 1). Transmission from the attended stimulus to C (left) is much higher than from the nonattended 1 (right). The spectral coherence score is calculated by averaging the spectral coherence in the non hatched region. B: spectral coherence scores of all 4 possible transmission combinations from stimuli to 2nd layer populations are plotted vs. the mixing parameter μ. Both stimuli are presented and S_A is attended. If μ = 0, i.e., S_A(S_B) does not elicit a response in population D(C), there is no significant information transmission via these pathways. For μ ≥ 0.3, i.e., in the range where the nonpreferred stimulus actually induces a response significantly bigger than zero (see Fig. 5A), the spectral coherence score is consistently higher for information transfer from the attended stimulus to both 2nd layer populations than from the nonattended stimulus.

Chance levels are calculated by the same procedure, pairing luminance signals with firing rates from different trials.

Error bars are obtained by bootstrapping. We assume the 50 simulated trials for every parameter combination from which we calculate the spectral coherence score to be a representative sample of the distribution. We apply bootstrap case resampling (Efron 1979) 100 times for every parameter combination and calculate the spectral coherence score for each. For every point in parameter space we thus obtain a distribution of 100 values of the spectral coherence score. The shaded areas in the plots show the 95% confidence interval.

We also determine the phase coherence PC at a specific frequency f and time t between two population rates x and y, which is given as

$${\text{PC}}_{xy}\left(f,t\right)=\frac{1}{N_k}\left|{\displaystyle \sum _{k=1}^{N_k}{e}^{i\left[\arg \left(W_x\left(f,t\right)\right)-\arg \left(W_y\left(f,t\right)\right)\right]}}\right|\cdot$$ (12)

W_x(f, t) denotes the wavelet transform of the rate x at the frequency f and time t, k the trial index, N_k the number of trials, and arg() the argument function (angle of a complex number with respect to the positive real axis). Possible values of the phase coherence lie between 0 (random phase relation) and 1 (complete phase locking). Note that this value does not give information on the actual value of the phase lag between x and y, only how stable this phase lag is over time and trials. This method is also used by Grothe et al. (2012).

Data analysis and visualization was performed using IPython (V1.1.0, http://ipython.org/, RRID:nlx 153939) (Pérez and Granger 2007); Numpy (V1.8.0, http://www.numpy.org/, RRID:nif-0000-32013); Scipy(V0.13.2, http://scipy.org/, RRID:nif-0000-10422) (Oliphant 2007); and Matplotlib (V1.3.1, http://matplotlib.org/, RRID:nif-0000-31991) (Hunter 2007).

RESULTS

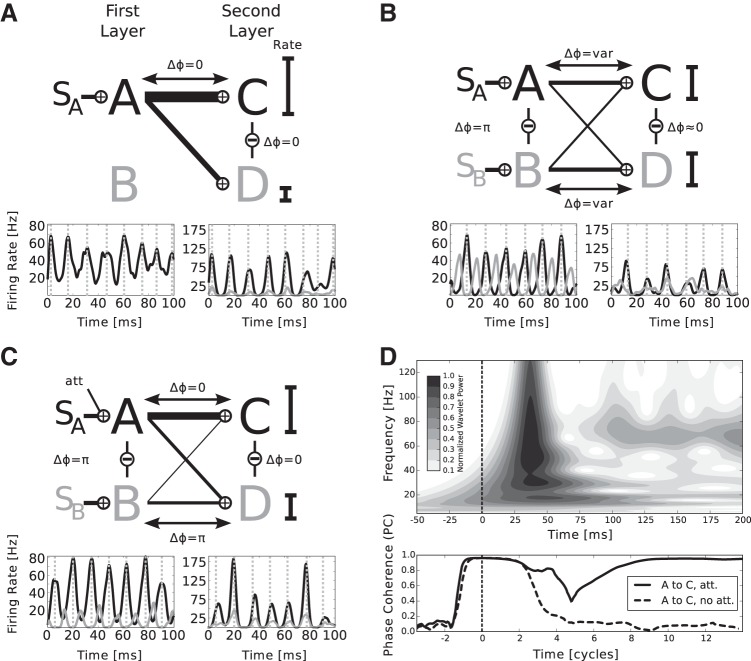
When the first layer populations are stimulated, by construction they engage in γ-oscillations. If only one stimulus is presented, say S_A, the second layer populations receive input according to their feed-forward connection probabilities and show respective firing rates, i.e., a high rate for a preferred and a low rate for a nonpreferred stimulus. The first layer population processing the attended stimulus, in this case A, entrains both C and D, setting a favorable phase relation for information transfer (Fig. 2A).

Fig. 2.

The mechanism of information routing and biased competition. The network architecture is symbolized by the simplified diagram in Fig. 1D. A: if 1 stimulus is present (here S_A), both 2nd layer populations are entrained by the corresponding 1st layer population. The phase is suitable for information transfer and the mean rates of C_exc and D_exc, symbolized by the black bars, scale monotonously with the feed-forward connection probabilities. The width of the lines connecting the 1st and 2nd layer corresponds to total input to the 2nd layer over the respective connection. A, bottom: example traces of mean firing rates of the excitatory subpopulations, where the line color corresponds to the color of the populations in the model diagram. The dashed gray lines mark the peaks of oscillations in A. For better visualization, the firing rate traces in the 1st layer are shifted to account for transmission delay and the phase shift between incoming currents peaks and rate peaks in the 2nd layer, such that rate peaks in the 1st layer are aligned with the corresponding peaks caused in the 2nd layer. Please note that the phase differences are calculated between currents, as described in materials and methods and not mean population rates, which we show for the sake of clarity. B: adding the 2nd stimulus (here S_B) brings A_exc and B_exc out of phase, whereas C_exc and D_exc tend to stay in-phase, due to the respective lateral interactions. The stimuli compete for representation in the 2nd layer. The outcome depends on temporal fluctuations in the peak rates of A and B. Thus the phases between the 1st and 2nd layer populations vary over time, favoring either A or B. Mean firing rates lie at approximately the mean of the 2 rates of C and D observed in A. C: symmetry is broken by adding an additional input representing the influence of attention. The higher rate of A_exc driven by the attended stimulus S_A more likely entrains populations C and D and thus renders input from B ineffective. The mean firing rates of A, where only the attended stimulus is present, are partially recovered. D: transient dynamics of the network shown in the interval of −50 to 200 ms after stimulus onset. Top: wavelet power spectrum of the mean firing rate of population C_exc (attention on S_A as in C), averaged over 100 trials. About 30 ms after stimulus onset (vertical dashed line), the population responds to the input with a strong, transient activation. Approximately 100 ms after stimulus onset, the population settles into a stable γ-rhythm with a frequency of ∼70 Hz. Bottom: amplitude of the phase coherence between A_exc and C_exc at a frequency of 70 Hz when S_A is attended (solid black line) and when no attention is involved (dashed black line). The abscissa is given in units of 70-Hz cycles. At stimulus onset, there is a period of almost complete “synchrony” since the feed-forward input arrives in every trial at the same point in time and leads to the same initial activation. Subsequently, γ-oscillations begin to emerge in both populations, which are initially in a random phase relationship (dip around 5 cycles poststimulus onset), and then become more and more coherent in the case of attention on S_A (solid line, after 9 cycles). Without attention, the phases remain on average in a random relationship leading to a low phase coherence amplitude.

Upon simultaneously presenting a second stimulus S_B, the inhibitory interaction in the first layer reduces mean rates of A_exc and B_exc and drives the populations out of phase. Simultaneously, the interactions between C and D bring both in-phase, entailing that if one stimulus is in a favorable in-phase relation, the other will be forced into a nonfavorable anti-phase relation with respect to both populations in the second layer. Which first layer population is in a favorable, and which is in a nonfavorable phase relation to C and D changes over time, depending on temporal fluctuations in the firing rates of A_exc and B_exc. It follows that both rates of C_exc and D_exc show approximately the same, normalized rate (Fig. 2B).

Attending to one stimulus, e.g., S_A, breaks the symmetry by raising the firing rate of A_exc and thereby reducing the rate of B_exc. The higher output of A_exc to the second layer results in a bias for A_exc to be in a favorable in-phase relation to transmit information to C, for which, in case of μ < 1, it is the preferred stimulus. At the same time, due to the in-phase relation between C and D mediated by the lateral interaction, it also enters a favorable phase relation with D. Consequently, the weaker output from B_exc will be in a nonfavorable phase relation to both C and D and hence less likely to elicit spikes in the second layer. Thus it is possible that if a nonpreferred stimulus is attended, here S_A with respect to D, the mean rate of the second layer population drops although the preferred stimulus is present at the same time (Fig. 2C).

Since synchrony emerges in a self-organized manner rather than being imposed by a common external source, coherent oscillations need a few γ-cycles to emerge. This behavior is most obvious at stimulus onset (Fig. 2D), where transient activation is followed by the organization of γ-activity. In particular, a stable phase relationship between an attended sending population in the first layer and the second layer populations takes approximately nine cycles (≈130 ms) to be fully established, thus imposing a temporal constraint on our CTC scheme. The transient of >100 ms is well in line with studies demonstrating that attention can only be shifted three to five times a second (Wolfe et al. 2000).

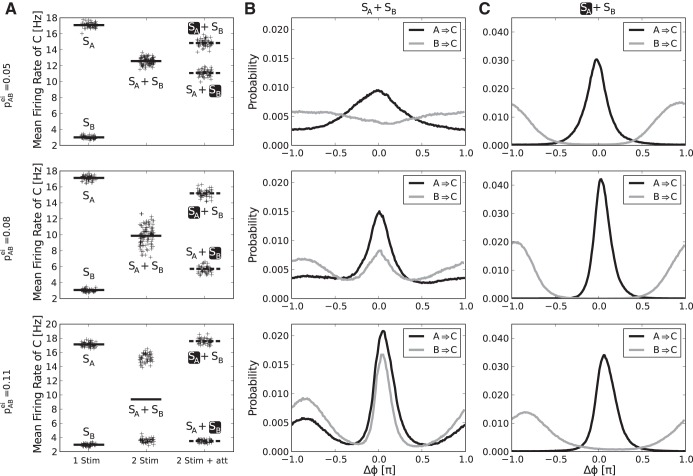
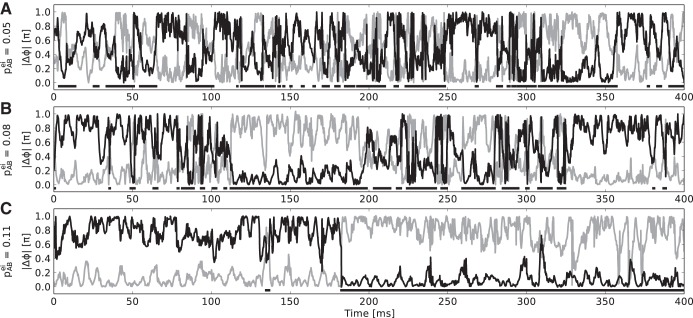
We find that especially the strength of lateral inhibition in the first layer, which realizes competition between A and B, determines the mode of operation of the network. Figure 3 shows the biased competition effect and respective phase difference distributions between first and second layer populations for different values of p_AB^ei. For weak competition in the “both stimuli, no attention” case, we observe weakly modulated monomodal phase distributions with broad peak widths between sending and receiving populations, implying a rather continuous and “mixed” representation of both stimuli over time in both populations C and D. The stronger the cross coupling gets, the more bimodal, peaked, and similar the phase distributions become (Fig. 3B). At the same time, the distribution of firing rates for the “both stimuli, no attention” case are also getting more and more bimodal, indicating a mode of bistable representation, where one stimulus is exclusively represented in the second layer for an extended period of time (Fig. 3A). Under attention, we find that the attended first layer population is almost exclusively in a favorable phase relation and the nonattended one in anti-phase, with virtually no overlap between the phase difference distributions. This holds for all values p_AB^ei (Fig. 3C). As a consequence, the rate recovery under attention is almost perfect in the bistable regime, i.e., with strong competition in the first layer (Fig. 3A, bottom). The emergence of bistability is further illustrated in Fig. 4, which shows example traces of the phase difference between populations A and C and the phase difference between B and C when both stimuli are present but none is attended. With increase in the lateral inhibition in the first layer, the dominance periods lengthen and the phase differences tend to be closer to the “best” (|Δϕ| = 0) and “worst” (|Δϕ| = 1) case and less in between (compare Fig. 3B).

Fig. 3.

Rate and phase distributions for different strengths of lateral inhibition in the 1st layer. A: plots show mean rates, denoted by lines, of population C_exc in response to different stimulus conditions: 1 stimulus present, 2 stimuli present, and 2 stimuli present while attending to 1. The focus of attention is marked by the black box. The black crosses around the mean rates show single trial values, jittered horizontally to better visually assess their distribution. The same plot is shown for 3 different strength of lateral inhibition between A and B, determined by the value of p_AB^ei. With increasing p_AB^ei, the response to presenting S_A and S_B at the same time becomes bimodal and the attentional rate recovery of the rates the stimuli elicit on their own becomes nearly perfect. B: plots show the phase difference distribution between A and C (A → C) and B and C (B → C) when both stimuli are present for the same three values of p_AB^ei as in A. We observe monomodal phase difference distributions between 1st and 2nd layer populations for p_AB^ei = 0.05. Population A, representing the preferred stimulus S_A, is more likely to be in-phase and population B, representing the nonpreferred stimulus, more likely in anti-phase. Increasing lateral inhibition causes the distributions to become bimodal and more similar, indicating a bistable regime where 1 stimulus is represented exclusively for an extended amount of time. C: same situation as B but with attention on S_A. The attended 1st layer population is mostly in-phase with the 2nd layer, the nonattended mostly in anti-phase, with virtually no overlap of the phase difference distributions. This effect is independent of the strength of lateral inhibition in the 1st layer.

Fig. 4.

Example traces for absolute phase differences |Δϕ| between A and C (black line) and B and C (gray line) for weak (A), intermediate (B), and strong (C) lateral inhibition in the 1st layer. Both stimuli are present but none is attended. The horizontal black bars indicate the time periods in which |Δϕ_AC| < |Δϕ_BC|, i.e., where population A is in a more favorable position to transmit information to C than B. With rising lateral inhibition, these dominance periods lengthen and the absolute phase differences tend to lie more closely to the edges of the spectrum, i.e., 1 respectively 0 (compare Fig. 3B).

A parameter that is furthermore important in a realistic setting is μ, describing relative stimulus preference, which in reality depends on the placing of the stimuli in visual space and the recording position in the cortex. Figure 5 shows the biased competition effect on firing rates over the full range of possible values for μ. We find that the general effect is present for all values (Fig. 5A) and that the intermediate response rate, when both stimuli are present but none is attended, lies approximately at the mean of the rates when only the preferred or nonpreferred stimulus is present (intermediate response factor ≈0.5; Fig. 5B), as reported in the literature (Reynolds et al. 1999; Moran and Desimone 1985). The biased competition score, showing how good the recovery of the single stimulus responses under attention is, lies around 0.6 to 0.8 for intermediate values of μ, with a bias for the higher, preferred rate. This nonsymmetric split up is also noted by Reynolds et al. (1999). In our model, this feature comes about due to the way attention is applied. Increasing the overall input to the first layer consequently increases the overall output to the second, increasing the activity averaged over the whole second layer.

Fig. 5.

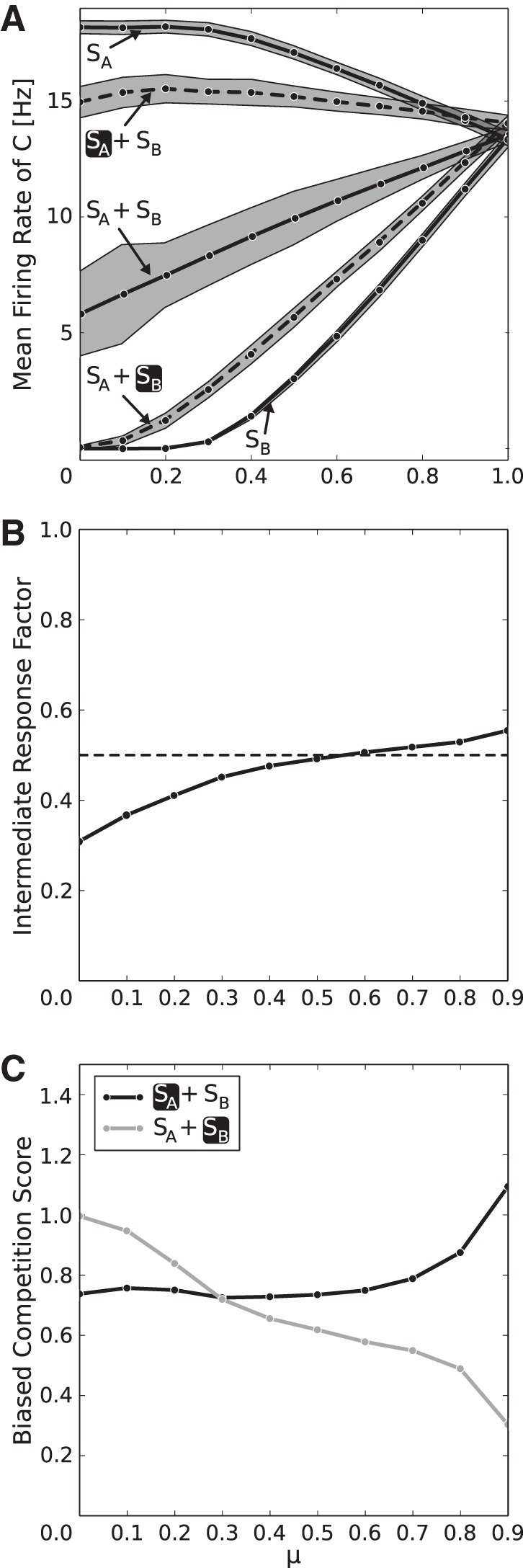
Biased competition effect for different values of the mixing parameter μ, which regulates the relative stimulus preference. A: in the 2nd layer, mean firing rates show consistent normalization if both stimuli are present (S_A + S_B) and partial attentional recovery (dashed lines, black box marks attentional focus) to the rates the stimuli elicit when presented alone (S_A/S_B) over the full range of possible values for μ. If μ = 0, S_B elicits no response in C, whereas if μ = 1, responses elicited by S_A and S_B are equally strong. The shaded areas visualize the SE. B: for values of μ ≥ 0.3, i.e., where the nonpreferred stimulus elicits a nonzero response (see A), we observe an intermediate response factor of ≈0.5, which means that the rate when both stimuli are presented lies approximately at the mean of the responses when only 1 stimulus is presented. C: in the same range, the biased competition score in population C, quantifying the degree to which single stimulus responses are recovered under attention, is ∼0.8 for preferred-rate recovery (black line) and around 0.6 for nonpreferred-rate recovery (gray line), revealing a slight bias of the attentional rate recovery for the preferred stimulus. A value of 1 would correspond to perfect rate recovery, whereas 0 would mean that attention has no effect on the firing rates.

We also investigated information transmission for the case that both stimuli were present and S_A was attended in the same parameter regimes using the method of Grothe et al. (2015): We computed the spectral coherence between the two competing, temporally modulated input stimuli and the neuronal activities in the second layer. Figure 6A shows an example of the spectral coherence for μ = 1. There was considerably stronger information flow from the attended stimulus S_A to the second layer populations than from the unattended stimulus S_B.

We again considered the variation of the parameter μ. For sufficiently large values of μ (≥0.3), i.e., where the stimulus S_A elicits a significant response in D (see Fig. 5A), the attended stimulus clearly dominates the activity of the second layer populations, specifically for μ = 1, which corresponds to the stimulus placement in the study of Grothe et al. (2015) (Fig. 6B).

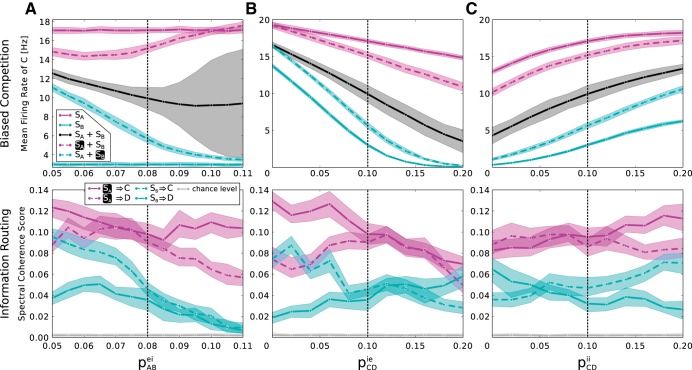
In addition to these primary results, also the general stability of both effects was investigated for variations of the connectivity parameters. Figure 7 illustrates the biased competition of mean rates and information routing for variations of p_AB^ei, p_CD^ie, and p_CDⁱⁱ. Qualitatively, the principal effects were observed across the whole parameter space, albeit at varying strengths, showing that the basic mechanisms are robust.

Fig. 7.

Robustness of biased competition and information routing to parameter variations. A–C, top: mean firing rate of C_exc in response to the different possible stimulus conditions (compare Fig. 5A) as a function of the strength of lateral inhibition in the 1st layer, controlled by p_AB^ei (A), the lateral coupling from inhibitory to excitatory neurons in the 2nd layer, controlled by p_CD^ie (B), and the lateral coupling between inhibitory neurons in the 2nd layer, controlled by p_CDⁱⁱ (C). μ Is set to 0.5. For all variations, the biased competition effect, i.e., the partial rate recovery under attention, remains intact. The SE around the intermediate rate, when both stimuli are present but none is attended, grows for high values of p_AB^ei due to the bimodal character of the rate distribution (compare Fig. 3A). A–C, bottom: spectral coherence score for variations of the same parameters (compare Fig. 6B). Also here, the main effect, meaning higher transmission from the attended stimulus to both 2nd layer populations under attention, is preserved over most of the parameter space. The dashed black lines mark the default value of the respective parameter.

We furthermore probed the susceptibility of information routing to neuronal noise in our framework. The amount of noise in the system was controlled by introducing a noise factor that scales all connection probabilities down and all synaptic weights up accordingly. This keeps the mean input to every neuron constant, i.e., preserves important quantities like absolute rates, while increasing the noise in the system by making single spikes more influential. Figure 8A shows that the selectivity of information transmission degrades gradually with increasing noise factor. The main reason is that a certain degree of recurrent connectivity is needed within the inhibitory subpopulations to generate a stable γ-rhythm. As p_locⁱⁱ decreases, this is no longer given. This point is illustrated in the insets of Fig. 8A that show example traces of the mean rate of A and B for a noise factor of 1 and 3.89. However, we find that the coefficient of variation of single spike train interspike intervals is widely distributed in a range between ∼0.35 and 1 as shown in Fig. 8B, in line with studies on the variability of neuronal responses in cortex (Softky and Koch 1993; Burns and Webb 1976). This holds also for conditions in which the noise factor is close to 1 and information transmission selectivity is optimal. The decrease of stability of the γ-rhythm generated by the inhibitory subpopulations is reflected in the notable increase in the coefficient of variation of inhibitory neurons with the noise factor.

Fig. 8.

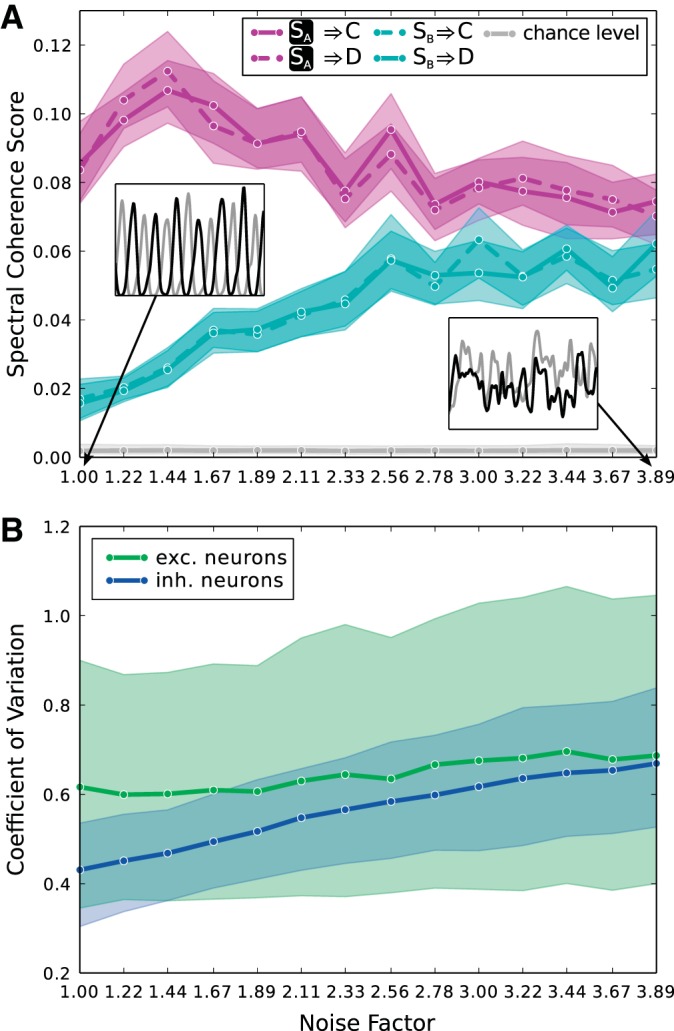
Robustness of information transmission to noise. A: noise in the system is increased by scaling all connection probabilities down and all synaptic weights up by the same noise factor. The plot shows the spectral coherence score for all 4 information transmission pathways for the case that both stimuli are present and S_A is attended. The mixing parameter μ is set to 1. Selectivity of information transmission from the attended stimulus to the 2nd layer degrades with increasing noise factor. The main reason is that as the recurrent connectivity within inhibitory subpopulations decreases, determined by p_locⁱⁱ, the γ-rhythms these populations generate get less and less stable. This fact is illustrated in the insets, which show example time courses of the mean activity of excitatory subpopulations in A (black) and B (gray) for noise factors of 1 and 3.89. B: coefficient of variation of interspike intervals of single neuron spike trains for all excitatory (green) and all inhibitory neurons (blue) in the network is displayed for various values of the noise factor. The solid lines denote mean values, and the shaded areas denote 75% confidence intervals. The increase of the coefficient of variation of inhibitory neurons correlates with the decreasing stability of generated γ-rhythms. Taken all neurons together, we observe coefficients of variation between ca. 0.35 and 1 over the whole range of the noise factor.

DISCUSSION

In summary, we designed a realistic, two-layered neural network, mimicking the converging feed-forward structure of the visual processing stream and incorporating intralayer lateral connectivity. The mechanism for information routing relies on anti-phase synchronization in the first layer and in-phase synchronization in the second layer, thereby introducing a phase competition between the driving, first layer populations. Attention is conceived in the most simple way, namely as an additional selective input to the first layer. The idea of utilizing a phase competition to selectively route information is a direct implementation of the CTC hypothesis (Fries 2005, 2009). Primarily we showed that both hallmark effects of visual attention, biased competition and information routing, can be successfully and robustly reproduced in a broad parameter regime, while single neurons show realistic response variabilities. As an explanation we found a twofold mechanism: firstly, by adding input to the first layer population processing the attended stimulus, its firing rate increases, leading to a stronger driving current targeting the second layer populations. At the same time, via the lateral connections, the increased activity in the attended population induces a decrease of activity in the unattended one, rendering its output to the second layer less effective. Secondly, this bias in the input of the higher area in favor of the attended population induces a phase relation between sending and receiving populations, which facilitates information transfer from the attended population and attenuates transmission from the unattended one.

Comparison to related models.

Other models put forward to explain information routing in biologically realistic networks of excitatory and inhibitory populations share certain commonalities: two distinct populations in one layer are connected to one population in a second layer, and competition between two stimuli is established ultimately by the fact that both first layer populations drive the same (or partly the same) inhibitory subpopulation in the second layer, be it directly or indirectly (Zeitler et al. 2008; Boergers et al. 2008; Wildie and Shanahan 2012; Deco and Rolls 2005). Of this, the model we propose is no exception. However, the lateral interactions we introduce are a novelty and allow our model to “self-organize” phase relations for stimulus selection and the use of a simple attentional direction signal, whereas in other approaches either a desired phase relation was “manually” constructed (Masuda 2009; Tiesinga and Sejnowski 2010) or oscillations were externally imposed (Zeitler et al. 2008; Wildie and Shanahan 2012). We specifically focus here on information-routing models based on oscillations but also other mechanisms not involving oscillations were proposed, e.g., utilizing specialized routing areas (Zylberberg et al. 2010) or nonlinear dendritic computation and hierarchical feedback propagation (Bobier et al. 2014).

Physiological plausibility.

Our model is structured as a self-consistent common motif in the visual pathway, where input from several cortical (hyper)columns in one area impinges onto the same (hyper)column in a higher area. Thus going upstream from the first layer to lower visual areas will result in even smaller receptive fields that have less mutual interactions, thereby exhibiting a negligible attentional selection effect. Going downstream to higher areas, populations targeted by the input will even more act as one single rather than two different computational units, thus the attentional selection effect would stay constant or even enhance further. From this insight we conclude that depending on size and placing of stimuli, the actual stage at which competitive lateral interaction occurs may vary. In the information routing experiments (Grothe et al. 2015; Bosman et al. 2012), activity from V1 and V4 was recorded. Identifying the second layer with V4, the first model layer, following the above reasoning, does not necessarily have to correspond to V1 but could be a more downstream area like V2 or even a different cortical layer within V4.

For explaining γ-oscillations in visual cortex, two mechanisms are deemed plausible: interneuron network gamma (ING) and pyramidal-interneuron network gamma (PING). Whether ING or PING mechanisms underlie oscillations in the visual cortex is still debated and might depend on task requirements (Tiesinga and Sejnowski 2009; Isaacson and Scanziani 2011; Buzsáki and Wang 2012; Gregoriou et al. 2015), but a combination of both seems most likely, considering the local connectivity structure (Haeusler and Maass 2007). In the current study, we focused on a “pure” ING-mechanism (no connections between excitatory and from excitatory to inhibitory subpopulations). However, we note that the specific implementation of the local and lateral connectivity is not of crucial importance. The proposed mechanism could be supported by any connectivity scheme that causes suppression and anti-phase synchronization in the first layer and in-phase synchronization in the second, while the local circuitry generates oscillatory activity. The only crucial constraint for effective routing to occur seems to be that γ-frequencies in all four populations are approximately equal. The specific value of this γ-frequency need not be fixed but may vary depending on stimulus properties as has been shown experimentally (Ray and Maunsell 2010). Stimulus-dependent changes in γ-frequency do not impede the routing mechanism as long as the frequencies of communicating populations covary. Dynamic frequency matching between V1 and V2 populations with overlapping receptive fields has indeed been demonstrated recently by Roberts et al. (2013). It can also be inferred that similar routing schemes could be used in different frequency bands, for example, in the β-range, which has been proposed to be a channel for top-down information flow (Buschmann and Miller 2007, 2009).

Another important model aspect is the attentional gating signal. We assume a tonic, additional input to the first layer. Apart from considering energy efficiency, a gating signal that is only used to “switch” the attentional state would also be more aesthetically pleasing. Tiesinga and Sejnowski (2010) ventured in this direction, showing that pulses applied to an inhibitory subpopulation can shift the phase of the whole population in dependency on the phase at which the pulse is applied. Simply substituting our additional input with such a pulsatile signal would likely not work, since the attentional selection firstly relies on rate differences in the first layer. However, if our system is in the bistable regime, applying a short pulse to one population in the first layer could tip the relation of firing rates to its favor, setting a suitable phase for information transfer. In this state, the system would remain for a relatively long time without necessary intervention. The difference to the work of Tiesinga and Sejnowski (2010) is that the generator of the attentional signal does not have to “know” the phases of all involved populations to select from. This intriguing alternative possibility of an attentional gating signal will be investigated more closely in future work. A further point of consideration is the target of the attentional signal. In our model, we apply it to the first layer. However, Buffalo et al. (2010) described a backward progression of latency and size of attentional effects, being fastest and strongest in V4 and latest and weakest in V1. This apparent disagreement can be potentially explained by differences in tasks: The stimuli used in the experiment by Buffalo et al. (2010) were set up far apart as to not cause biased competition in the recorded V4 neurons. We conceptualize attention as a mechanism to resolve competition. We hypothesize that an attentional signal would be most effective at the stage of strongest competition (layer 1 in our model) before both stimuli are integrated in a successive processing stage, thus it is well conceivable that the area attention targets also depends on the stimulus and task configuration. Given the specific stimulus setup, this target area could well be V4 in the aforementioned experiments, meaning that V4 would correspond to layer 1 in our model, thereby not contradicting our approach.

Predictions of the model.

The model mechanisms for selective routing imply that attention can be traded against bottom-up stimulus saliency: if two stimuli of different saliency elicit different firing rates in the first layer, the weaker stimulus cannot be gated unless its associated firing rate in the first layer is enhanced by attention to be higher than the rate elicited by the unattended one. Hence it may be possible to construct pairs of stimuli with strong enough luminance or contrast difference such that the weaker stimulus cannot be attended any more. Although this has not been shown directly to our knowledge, the prediction is supported by several studies showing that attention acts similar to a contrast gain (Martinez-Trujillo and Treue 2002; Reynolds and Desimone 2003; Carrasco et al. 2004). In a setting similar to Grothe et al. (2015), our prediction could be tested by using two flickering stimuli with the same flicker amplitude but different mean luminance.

Since effective stimulus competition and routing in our model requires anti-phase synchronization between the two first layer populations, a further prediction is that we expect the phase difference between these populations to depend on the distance of the competing stimuli. This translates to the placing of stimuli in visual space in retinotopically organized areas if the competing feature is location in visual space [fully the case in Grothe et al. (2015) and partially in Moran and Desimone (1985) and Reynolds et al. (1999)]. More specifically, populations in close cortical vicinity should oscillate in phase, whereas at some “optimal” distance the oscillations should be out of phase. However, note that distance is not necessarily difference of locations but could be analogously defined for other receptive field dimensions such as orientation or color. To our knowledge, the dependency of oscillation phases on cortical distance or tuning property in visual cortex while two competing stimuli are presented has not been investigated to date.

In addition to the primary effects of biased competition and selective gating, we found that by increasing lateral inhibition in the first layer, the system transitions into a bistable regime. Bistability has also been found as an emergent model feature by Wildie and Shanahan (2012), where it too depends on the strength of lateral inhibitory interactions, albeit in the second model layer. We note that multistability is an inherent feature of a subset of oscillating, delay coupled networks with lateral inhibition that is not restricted to the specific realization in this model. A well-studied example of bistable perception is binocular rivalry, the alternating percept that is observed when two different stimuli are presented monocularly to corresponding retinal locations [see Blake (2001) for a comprehensive review]. Current theories propose that the bistability of the percept is at least in part attributable to interocular inhibition between monocular neurons in V1 and/or LGN (Tong et al. 2006), which concurs with our model architecture if we consider distance in the ocularity dimension [close (same eye) or far (other eye)].

By extending the distance-dependent architecture to other stimuli dimensions, we predict that the locus at which rivalry is initiated depends on the features of the stimuli that are in competition, e.g., orientation differences will elicit bistable dynamics early in the visual system, whereas the neural correlate of shape ambiguities will be found in higher areas where neurons with respective receptive field properties are located. Consequently we expect that rivalry effects of competing stimuli that differ in several stimulus dimensions can be spread out through the whole visual system, consistent with the explanation for binocular rivalry that Tong et al. (2006) promote.

GRANTS

This research project was funded by the Bundesministerium für Bildung und Forschung (Bernstein Award Udo Ernst Grant 01GQ1106).

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the author(s).

AUTHOR CONTRIBUTIONS

Author contributions: D.H., U.A.E., and K.R.P. conception and design of research; D.H. performed experiments; D.H. analyzed data; D.H., U.A.E., and K.R.P. interpreted results of experiments; D.H. prepared figures; D.H. drafted manuscript; D.H., U.A.E., and K.R.P. edited and revised manuscript; D.H., U.A.E., and K.R.P. approved final version of manuscript.