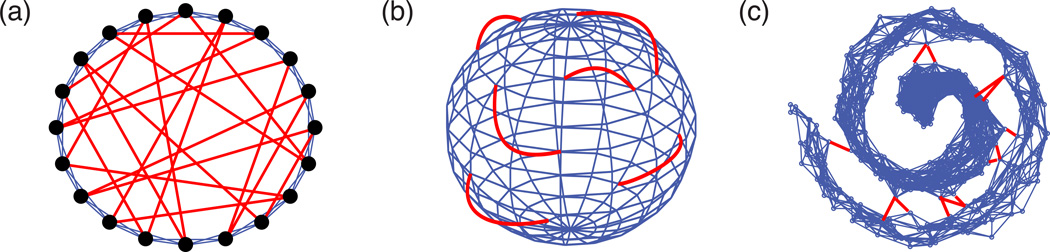
FIG. 1. Examples of noisy geometric networks.
Nodes are embedded in three manifolds: (a) a ring (1D) embedded as a circle in ℝ2; (b) a spherical surface (2D) in ℝ3; and (c) a bounded plane (2D) embedded (nonlinearly) in ℝ3 in a configuration known as the “swiss roll” [22]. Given a network with “geometric edges” (blue), in panels (a)–(b), we add “non-geometric edges” (red) uniformly at random. In panel (c), by contrast, we add noise to the nodes’ locations in the ambient space and place edges between nodes that are nearby in that space. In this scenario, we interpret edges between nodes that are nearby with respect to the ambient space but not the manifold as the nongeometric edges.