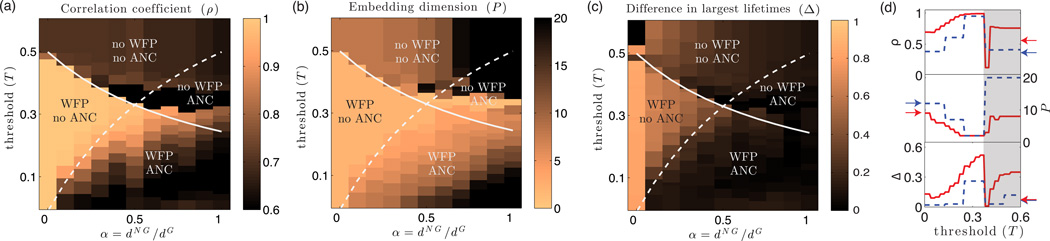
FIG. 6. Analyzing manifold structure in contagion maps.

We analyze the point clouds of WTM maps for various thresholds T for noisy ring lattices with N = 200 and various ratios α = d^(NG)/d^(G). (As an example, we show results for d^(G) = 20 and various values of d^(NG).) For each point cloud, we study (a) geometry through ρ, (b) dimensionality through P, and (c) topology through Δ (see the text and the Methods section). The transitions between qualitatively different structures in the WTM maps (i.e., as seen through ρ, P, and Δ) closely resemble the bifurcation structure from Eqs. (1) and (2), which we show for k = 0 using solid and dashed curves, respectively. In panel (d), we fix α = 1/3 and plot ρ, P, and Δ as a function of threshold T. We show results for (d^(G), d^(NG)) = (6, 2) (blue dashed curves) and (24, 8) (red solid curves). Note that there are activation times that are infinite for $T\ge T_0^{(\mathrm{W}\mathrm{F}\mathrm{P})}=3/8$ [shaded region in (d)]. The arrows indicate the ρ, P, and Δ values that we obtain for the embedding of nodes based on shortest paths, which (as we discuss in the text) one can construe as a variant of the dimension-reduction algorithm Isomap [22].