Fig. 5.

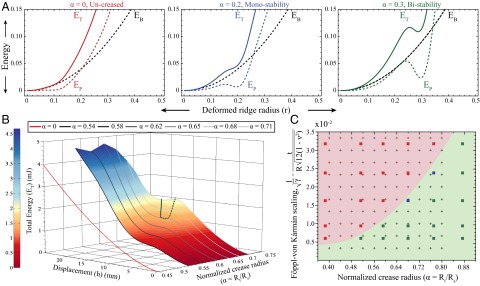
Stability of creased spherical shells (K > 0). (A) For an uncreased shell, the energy of an indented shell is composed of the bending energy $E_B$ (black dotted) and the Pogorelov ridge $E_P$ (colored dotted). For a creased shell $E_P$ takes a substantial dip localized at $r\sim R_t$, but the total energy $E_T$ (colored solid) only has a local minimum if the crease is large enough. In these schematics the function $t\left(r\right)$ is chosen to mimic the profile provided by experimental molds. (B) Numerically calculated energy landscape for a creased shell with $\gamma \approx {10}^4$ for a variety of α. The Pogorelov solution is recovered for $\alpha =0$ (red plot), whereas for small values of α the energy gain from the crease is insufficient to create a local minimum. However, above a critical α, local minima (solid green) and maxima (dashed green) bifurcate to generate a region of stability. (C) Phase diagram for snapping behavior of spherical shells over a wide range of geometrical parameters α and $1/\sqrt{\gamma }$. Stability behavior in experiments is characterized as bistable (, switches to folded state through a snapping mechanism), monostable (, prefers unfolded state), or temporarily stable (, closer to phase boundary: snap back on a timescale of seconds without external perturbations). Finite-element simulations (points solved denoted with +) provide regions of monostability (red shading) and bistability (green shading). Each experimental data point was analyzed for at least three shells of appropriate parameters.