Modeling the growth dynamics of glioblastoma using magnetic resonance imaging

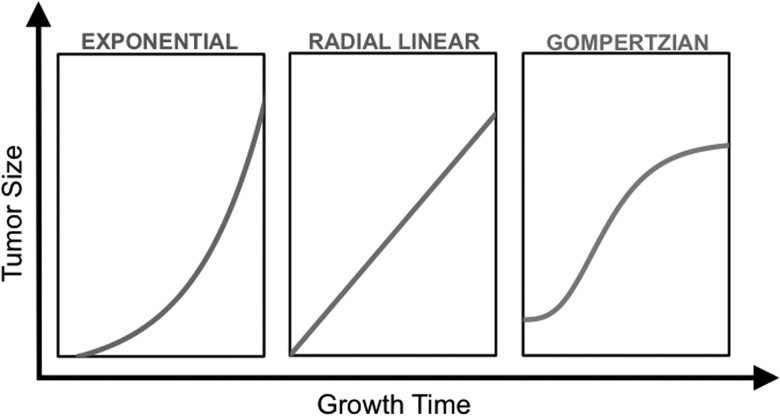
The significant intra- and intertumoral heterogeneity of gliomas, an improved appreciation for the biological differences among individual tumors, and the complexity of response assessment have led to increased interest in radiological modeling of glioma growth. The development of such models has been challenging due to the intra- and intertumoral heterogeneity of gliomas, as well as unique features of gliomas, including invasive growth, cellular migration, and differential tumor dispersion in gray and white matter.^1,2 Tumor growth is determined by the complex interactions among proliferation, angiogenesis, and dispersion balanced by necrosis, apoptosis, and cell death. Three primary growth patterns have been proposed to explain tumor growth rates: the exponential pattern, radial linear pattern, and Gompertzian growth pattern (Fig. 1). The exponential growth model is based on the assumptions that tumors have a constant volume doubling time, and thus the size of the tumor increases exponentially with time. Conversely, the radial linear growth model assumes that the mean linear radius increases linearly with time. The Gompertzian model assumes initial exponential growth which then slows to linear growth as tumor volume increases before reaching a plateau. However, the clinical evidence to support one growth model over another in untreated tumors has been sparse.

Fig. 1.

A schematic illustration of different growth models depicting tumor size as a function of time.

The study by Stensjøen and colleagues in this issue of Neuro-Oncology makes a significant contribution in this regard.³ The authors performed a retrospective analysis of the rate and growth dynamics of untreated solitary glioblastoma multiforme (GBM) in adults over more than a decade. Analysis of 106 consecutive, pretreatment, contrast-enhanced T₁-weighted MRI scans, acquired at least 2 weeks apart, demonstrated that although GBM growth rate varied significantly among individuals, smaller tumors had faster growth rates than larger lesions. Interestingly, the central nonenhancing regions within contrast-enhancing tumors also appeared to grow more quickly than the contrast-enhancing regions or the entire tumor mass. Their data demonstrate that the radial linear and Gompertzian growth models are more consistent with the observed growth dynamics than the exponential model.³ The authors also note that due to rapid growth—particularly in small and medium sized tumors (<3.88 mL and between 3.88 and 36.88 mL, respectively)—delays in care could potentially have significant adverse effects on patient outcomes.

Only a handful of previous imaging studies have attempted to model tumor growth in pretreatment gliomas in such large image sets. Yamashita et al⁴ reported one of the earliest studies measuring in vivo GBM growth rates based on contrast-enhanced CT imaging at the time of recurrence. Blankenberg et al⁵ demonstrated direct linear correlation between volume doubling time and survival using MRI, but similar to previous studies, the data were obtained only after treatment was completed or at the time of recurrence. The largest series, by Wang et al,⁶ which modeled growth dynamics of patients with untreated GBM using MRI, comprised only 32 patients. Interestingly, these authors also validated the utility of the radial growth model and demonstrated that modeling tumor growth and invasiveness in untreated GBM using this model could predict patient prognosis.⁶

The strength of the present study is the availability of large numbers of preoperative MRI on patients with GBM over an interval of 2 weeks or more.³ However, the study also has several limitations. While the preoperative images (at the second timepoint) were centrally obtained and of uniformly high quality, the baseline diagnostic images used in the calculation (the first timepoint) were performed at numerous hospitals with various types of scanners, different field strengths, different slice thicknesses, and different imaging parameters, which limits the precision of their data. In addition, in the sub-analysis of contrast enhancing and nonenhancing volumes, the time-dependent change in tumor enhancement after contrast administration was not considered.⁷ While the findings made by Stensjøen et al are intriguing, their primary analysis focused on differences in the growth rates of the enhancing and nonenhancing parts of the tumors and (in their supplementary analysis) on differences in growth rates among gliomas classified into 3 size categories. This is difficult to translate to the management of individual patients and (presumably) is applicable to only GBM, thus excluding lower-grade gliomas, which rarely have enhancement. Moreover, it does not account for other differences in imaging that might be attributable to intra- and intertumoral heterogeneity in GBM.

Gliomas are unique in that they are the only cancer in which nearly all of the morbidity is due to local progression (ie, within the brain). Consequently, better modeling of glioma growth and response to treatment is likely to have greater prognostic and therapeutic implications for glioma than for other diseases. Stensjøen and colleagues have made a novel and potentially useful contribution toward this important goal. Given the complexity and importance of the problem, continued research efforts are necessary to better understand and model growth and invasiveness of gliomas. An ideal model would provide insight into glioma growth and invasion, metabolism, and response to treatment across tumor grades and types, be objective and reproducible across imaging platforms, as well as be customizable for counseling individual patients. Quantitative imaging paradigms, which provide more precise and accurate data, should be applied in future studies. Advanced imaging tools such as PET, perfusion, spectroscopy, and diffusion tensor imaging may also improve our understanding of the multidimensional tumor growth processes in gliomas compared with routine MRI.⁸ Magnetic resonance fingerprinting, which rapidly and noninvasively quantifies multiparametric tissue properties, is another robust and objective tool which may also be potentially useful for quantification of early tumor growth and detection of tissue invasion.⁹

Funding

CB funding: None. AES is supported by the Peter D. Cristal Chair in Neurosurgical Oncology as well as the Kimble endowment for Neurosurgical Oncology.

Conflict of interest statement. None declared for both authors.