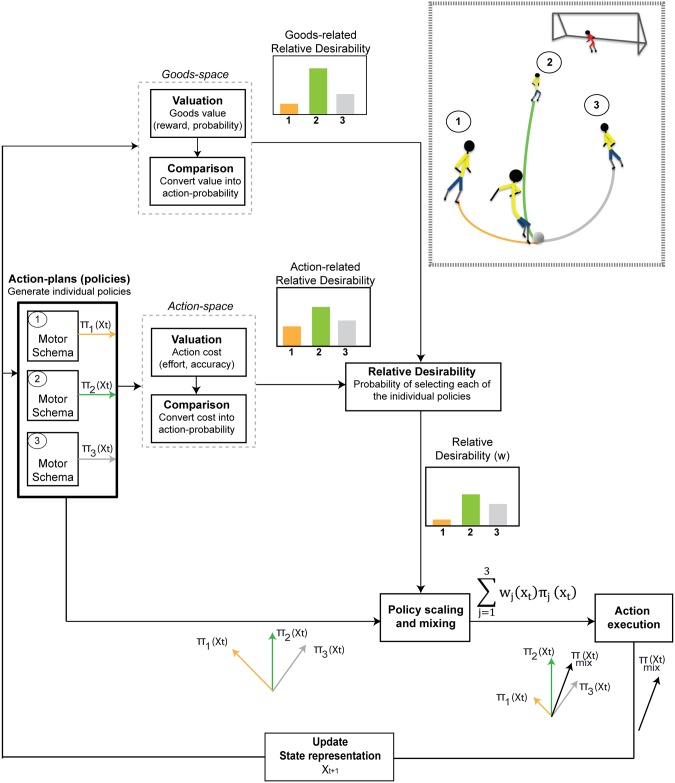
Fig 2. The architectural organization of the theory.
It consists of multiple stochastic optimal control schemes where each of them is attached to a particular goal presented currently in the field. We illustrate the architecture of the theory using the hypothetical scenario of the soccer game, in which the player who is possessing the ball is presented with 3 alternative options—i.e., 3 teammates—located at different distances from the current state x t. In such a situation, the control schemes related to these options are triggered and generate 3 action plans (u 1 = π 1(x t), u 2 = π 2(x t) and u 3 = π 3(x t)) to pursue each of the individual options. At each time t, desirabilities of the each policy in terms of action cost and good value are computed separately, then combined into an overall desirability. The action cost of each policy is the cost-to-go of the remaining actions that would occur if the policy were followed from the current state x t to the target. These action costs are converted into a relative desirability that characterizes the probability that implementing this policy will have the lowest cost relative to the alternative policies. Similarly, the good value attached to each policy is evaluated in the goods-space and is converted into a relative desirability that characterizes the probability that implementing that policy (i.e., select the goal i) will result in highest reward compare to the alternative options, from the current state x t. These two desirabilities are combined to give what we call “relative-desirability” value, which reflects the degree to which the individual policy π i is desirable to follow, at the given time and state, with respect to the other available policies. The overall policy that the player follows is a time-varying weighted mixture of the individual policies using the desirability value as weighted factor. Because relative desirability is time- and state- dependent, the weighted mixture of policies produces a range of behavior from “winner-take-all” (i.e., pass the ball) to “spatial averaging” (i.e., keep the ball and delay your decision).