Clinically feasible NODDI characterization of glioma using multiband EPI at 7 T

Abstract

Recent technological progress in the multiband echo planer imaging (MB EPI) technique enables accelerated MR diffusion weighted imaging (DWI) and allows whole brain, multi-b-value diffusion imaging to be acquired within a clinically feasible time. However, its applications at 7 T have been limited due to B1 field inhomogeneity and increased susceptibility artifact. It is an ongoing debate whether DWI at 7 T can be performed properly in patients, and a systematic SNR comparison for multiband spin-echo EPI between 3 T and 7 T has not been methodically studied. The goal of this study was to use MB EPI at 7 T in order to obtain 90-directional multi-shell DWI within a clinically feasible acquisition time for patients with glioma. This study included an SNR comparison between 3 T and 7 T, and the application of B1 mapping and distortion correction procedures for reducing the impact of variations in B0 and B1. The optimized multiband sequence was applied in 20 patients with glioma to generate both DTI and NODDI maps for comparison of values in tumor and normal appearing white matter (NAWM). Our SNR analysis showed that MB EPI at 7 T was comparable to that at 3 T, and the data quality acquired in patients was clinically acceptable. NODDI maps provided unique contrast within the T2 lesion that was not seen in anatomical images or DTI maps. Such contrast may reflect the complexity of tissue compositions associated with disease progression and treatment effects. The ability to consistently obtain high quality diffusion data at 7 T will contribute towards the implementation of a comprehensive brain MRI examination at ultra-high field.

Highlights

• •NODDI characterization of glioma at 7 T within 6 min with multiband EPI
• •An SNR comparison was performed between 7 T and 3 T SE-EPI.
• •SNR was comparable between 7 T and 3 T multiband SE-EPI.
• •NODDI maps provided unique contrast within the glioma T2 lesion.

1. Introduction

It is estimated that 68,470 new cases of primary brain and central nervous system tumors are expected to be diagnosed in the United States in 2015, and gliomas account for the majority of primary malignant brain tumors in adults (Ostrom et al., 2014). Although low-grade lesions have a better prognosis, they often undergo transformation to a more malignant, higher grade at the time of progression. Both primary and recurrent gliomas infiltrate into adjacent brain tissue, making it difficult to define tumor margins. Proper diagnosis and grading, correct localization, and assessment of response to therapy are of great importance for all phases of treatment planning and selection.

Conventional T1- and T2-weighted MRI are applied in conjunction with an injection of a Gadolinium-based contrast agent to delineate structural abnormalities in the brain and assess regions where the brain–blood barrier has been compromised. However, these conventional anatomic sequences have failed to reliably distinguish between complex tissue components within and around brain tumors such as interstitial edema, gliosis, inflammation, cysts, necrosis and active tumor. The specificity of conventional MRI is further compromised by treatment with radiation, temozolomide and anti-angiogenic agents (Wen et al., 2010).

Diffusion weighted imaging (DWI) has been a rapidly expanding field in MRI and has been found valuable in evaluating many diseases in the brain (Lerner et al., 2014; Rovaris et al., 2005; van Everdingen et al., 1998). By sensitizing MR signal to the random motion of water molecule protons at a microscopic level (of the order of 5–20 µm), it is able to probe tissue microstructures in the brain such as axons, dendrites, glial cells, and extra-cellular spaces (Yablonskiy and Sukstanskii, 2010), in a manner that may provide valuable insights into tumor physiology. A simple and most widely used model to describe changes in signal intensity is diffusion tensor imaging (DTI), where the directional motion of water behavior is characterized by a 3 dimensional tensor. The apparent diffusion coefficient (ADC) derived from tensor modeling is a sensitive yet non-specific metric when evaluated in the highly heterogeneous tumor environment. On serial MRI studies, reduction in ADC may be the result of decreasing vasogenic edema or an increase in cell density. Increased ADC may reflect tissue necrosis, an increase in interstitial fluid, or a decreasing cell density due to effective treatment. The ability to distinguish between the mechanisms that lead to changes in ADC would be very important for treatment planning and monitoring patients. One approach to addressing this problem is to use a more sophisticated diffusion model that can distinguish between the different tissue compartments.

Neurite Orientation Dispersion and Density Imaging (NODDI) is a recently proposed diffusion model that allows the quantification of specific microstructural features directly related to neuronal morphology (Zhang et al., 2012). In particular, the NODDI model ascribes the signal from water protons in neuronal tissue to one of three different pools: i) free water in areas such as the ventricles that contain CSF and exhibit isotropic diffusion; ii) restricted water within linear structures that represent dendrites and axons; and iii) water that is anisotropically hindered, representing diffusion within glial cells, neuronal cell bodies and extracellular environment. An orientation dispersion index (OD) is produced to describe the coherence of neurite directions, with a lower value indicating more coherent organization. The optimized 30-minute protocol limited the NODDI model to a 2-shell 90-direction DWI acquisition, which has been shown to produce reliable NODDI maps (Zhang et al., 2012). Recent applications of NODDI that have provided encouraging results are from patients with multiple sclerosis (Magnollay, 2014; Schneider et al., 2014), focal cortical dysplasia (Billiet et al., 2014; Winston et al., 2014), neurofibromatosis (Billiet et al., 2014), healthy newborn brain (Kunz et al., 2014), as well as in the spinal cord (Grussu et al., 2015). These results are all at 3 T, and the method has not yet been investigated at 7 T, or in patients with brain tumors. The technique is enticing for the evaluation of patients with glioma, in that we hypothesize that changes in vasogenic edema would be reflected in the free water compartment (Stummer, 2007), and changes in cell density would be associated with changes in the hindered water compartment.

The availability of improved hardware and fast acquisition techniques make it possible to obtain 90-directional multi-shell DWI within a clinically feasible time. Conventional parallel imaging (Blaimer et al., 2004; Deshmane et al., 2012) results in a significant loss in SNR because the number of phase encoding steps that are acquired is reduced. For 2D multi-slice imaging, significant improvements can be achieved by exciting several slices at the same time using multiband radio frequency (RF) pulses. Since each slice is excited and sampled identically without skipping or missing k-space data, there is no loss of SNR due to reduced acquisition time as is encountered with parallel imaging. This technique has been successfully implemented in the highly publicized Human Connectome Project for accelerated diffusion imaging acquisition at 3 T (Setsompop et al., 2013; Sotiropoulos et al., 2013). At higher field strengths, reduced T2 compromises the gain in SNR from the increased static magnetization, making the benefit of diffusion imaging at ultra-high field unclear. Other challenges, such as increased B0 and B1 field inhomogeneity, can also influence the quality of diffusion data at high field (Uğurbil et al., 2013). Wu et al. (Wu et al., 2013) have attempted to compensate for the B1 inhomogeneity through RF shimming of multiband pulses in both single and parallel transmit settings. Another group has also implemented the multiband spoke technique to both improve the B1 homogeneity across slices and reduce peak RF power (Sharma et al., 2015). With the efforts put into the optimization for acquisition of diffusion data at 7 T, it has been anticipated that the diffusion data set acquired with a more powerful gradient set at 7 T will be comparable to 3 T data (Uğurbil et al., 2013). Despite these advances, the applications of ultra-high field diffusion weighted imaging have been limited, and there has not yet been a rigorous direct comparison of the SNR for diffusion imaging between 3 T and 7 T.

The goal of this study was to use multiband DWI at 7 T in order to obtain 90-directional multi-shell data within a clinically feasible acquisition time for patients with glioma. This study included an SNR comparison between 3 T and 7 T, and the application of B1 mapping and distortion correction procedures for reducing the impact of variations in B0 and B1. The optimized multiband sequence was applied to generate both DTI and NODDI maps and to compare the values in tumor and normal appearing white matter (NAWM).

2. Data acquisition

2.1. Multiband acquisition

Multiband EPI was conducted with a quadrature transmit and 32-channel receive head coil (Nova Medical, Wilmington, MA) on GE scanners. Three slices (40 mm apart) were simultaneously excited (multiband factor of 3, or MB = 3) with a three-band RF excitation (no inter-slice shift) and axial spin-echo echo planer (SE-EPI) readout with phase encoding (PE) in the anterior–posterior (AP) direction, resulting in 60 slices for whole brain coverage with isotropic voxels of 2 × 2 × 2 mm³ over a field of view of 256 × 256 mm². 75% partial Fourier k-space sampling was employed to reduce TE and an in-plane acceleration factor of 3 (R = 3) was used, which we found to be the best trade-off between TE and distortion. With a 50 mT/m amplitude gradient system at b = 2000 s/mm², TE was 71.6 ms and TR was 3200 ms. Calibration images were acquired at the beginning of the sequence with the same three-band excitation pulses but with different phase offsets applied between the bands so that they could be separated through a Fourier Transform (FT). This used the same SE-EPI readouts but was interleaved three times to fully sample k-space while having the same k-space traversal speed as the actual accelerated acquisition.

A B1 mapping procedure was performed prior to the multiband acquisition to determine the optimal transmit gain (TG) (D. Kelley, 2013) that can account for the B1 inhomogeneity at high field. B1 maps were generated using a gradient echo acquisition sequence (TR/TE = 250/8 ms) with a 1 ms adiabatic Bloch–Siegert pulse and the transmitter gain was automatically adjusted based on the median B1 of the image volume.

To correct for the susceptibility-induced distortion, one additional b = 0 image was acquired with reversed phase encoding blips using the same multiband sequence. This resulted in a pair of b = 0 images with distortions going in opposite directions and allowed the off-resonance field to be estimated with a method similar to that described in Andersson et al. (2003) and implemented in FSL (Smith et al., 2004). The correction was then applied for the other DWIs.

2.2. Volunteers' data acquisition for SNR comparison

5 volunteers were scanned with both GE 3 T MR 750 and GE 7 T MR950 scanners (GE Healthcare, Waukesha, WI) using 32-channel receive-only head coils (Nova Medical, Wilmington, MA) and the same gradient system (50 mT/m amplitude and 200 T/m/s slew rate). Ten b = 0 (T2 weighted) images were repetitively acquired with both standard EPI (MB = 1) and MB = 3 using the acquisition parameters described above. With the same TR, only the central slab of the brain was acquired for MB = 1.

2.3. Phantom data acquisition for determination of g factor maps

A homogeneous spherical water phantom was used to evaluate the geometry factor (g-factor) map which quantifies the fractional loss in SNR caused by the non-orthogonality of the array coil sensitivities (Pruessmann et al., 1999). Two data sets were acquired in each scanner using a gradient-recalled echo (GRE) imaging sequence (FOV = 256 × 256 mm², matrix size = 64 × 64, slice thickness = 2 mm). The first data set was used to assess the noise covariance matrix and was obtained with all RF pulses suppressed. The second data set served to determine coil sensitivity maps for each coil element and was obtained with regular RF excitation.

2.4. Patients' NODDI data acquisition

Twenty patients with glioma (13 males and 7 females, median age = 54 years) were referred by physicians from the neuro-oncology service at our institution and recruited to this study. The characteristics of the patient population are summarized in Table 1. Tumors had been graded by histological examination of tissue samples obtained during biopsy or surgical resection: 10 had grade II, 3 had grade III and 7 had grade IV. All patients were recurrent and 4 patients were showing progressive disease at the time of the scan.

Table 1.

Characteristics of patients.

No.	Age	Sex	Grade	RT	Chemotherapy	Disease state	Image comments
1	59	M	2	Yes	TMZ	Recurrent	Stable
2	65	M	4	Yes	TMZ	Recurrent	Stable
3	48	M	2	Yes	None	Recurrent	Stable
4	68	F	2	Yes	TMZ	Recurrent	Progressive disease
5	60	F	3	Yes	TMZ	Recurrent	Stable
6	34	M	2	No	None	Recurrent	Stable
7	50	M	3	No	TMZ	Recurrent	Stable
8	44	F	4	Yes	TMZ	Recurrent	Progressive disease
9	48	M	4	Yes	TMZ	Recurrent	Progressive disease
10	59	M	2	Yes	TMZ	Recurrent	Stable
11	40	M	2	No	None	Recurrent	Stable
12	41	F	4	Yes	TMZ	Recurrent	Stable
13	65	M	2	Yes	RAD001	Recurrent	Stable
14	46	M	4	Yes	TMZ	Recurrent	Stable
15	57	F	4	Yes	None	Recurrent	Stable
16	55	M	4	Yes	TMZ	Recurrent	Stable
17	27	F	2	Yes	None	Recurrent	Stable
18	60	F	3	Yes	TMZ	Recurrent	Stable
19	52	M	2	Yes	TMZ	Recurrent	Stable
20	75	M	2	Yes	None	Recurrent	Progressive disease

A two-shell diffusion imaging protocol was acquired on the 7 T scanner with MB = 3. This protocol included 7 b = 0 images (and one additional b = 0 image with reversed phase-encoding gradient for distortion correction), 30 directions at b = 1000 s/mm², and 60 directions at b = 2000 s/mm² with a total acquisition time of 5′ 42″.

Anatomical images of these patients were acquired at the 3 T scanner, including sagittal T1-weighted spin echo, axial fluid attenuated inversion recovery (FLAIR), contrast-enhanced 3D spoiled gradient-recalled acquisition in the steady state (SPGR) T1-weighted and T1-weighted post-contrast spin echo images (T1-gad). In 14 patients, 24-directional DWI with a standard SE-EPI sequence was also acquired (repetition time (TR)/echo time (TE) = 10 s/99 ms, voxel size = 2×2 × 2 mm³, in-plane R = 2, b = 1000 s/mm²).

Table 2 summarized the data acquisition with phantom, volunteers and patients.

Table 2.

Summary of data acquisition with phantom, volunteers and patients.

	Phantom		Volunteer		Patient
Purpose	g-Factor estimation		SNR comparison		NODDI characterization
# subjects	1		5		20
Scanner	3 T	7 T	3 T	7 T	3 T	7 T
Sequences	GRE RF on GRE RF off	GRE RF on GRE RF off	MB1 MB3	MB1 MB3	T1-nogad T2 FLAIR T1-gad Standard DWI	MB NODDI

2.5. Postprocessing and analysis

2.5.1. Multiband image reconstruction

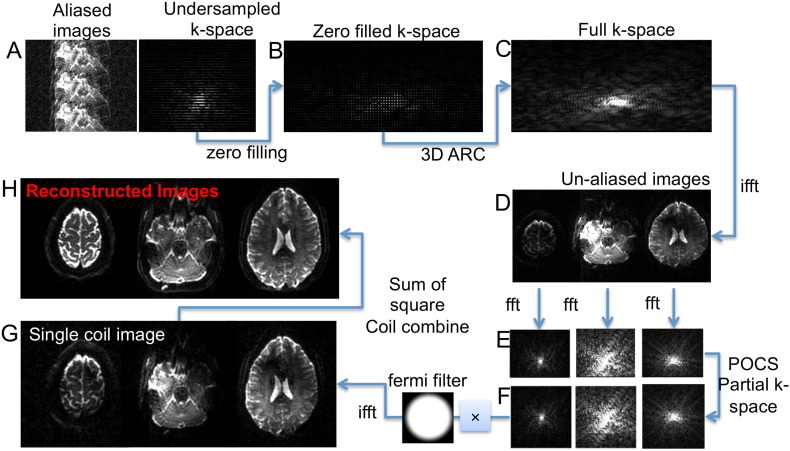
The image was aliased in both SI and AP directions, and was unfolded using the SENSE/GRAPPA procedure as described in Blaimer et al., (2004). The calibration data were first concatenated and Fourier transformed (FT) to generate the fully sampled k-space. Once the kernel has been generated, aliased images went through the reconstruction pipeline as illustrated in Fig. 1. The undersampled k-space was first zero filled in the direction that no acceleration was performed (left–right, Fig. 1B) and a standard GRAPPA/ARC procedure was applied to reconstruct the k-space data (Fig. 1C). After an inverse Fourier Transform (ifft), the unaliased images (Fig. 1D) were individually transformed into k-space again (Fig. 1E) to reconstruct the full k-space (Fig. 1F) through a partial k-space reconstruction method using projection onto convex sets (POCS) (Yudilevich and Stark, 1989). A 2D Fermi filter was then applied to reduce Gibbs ringing, and single coil images (Fig. 1G) were combined with a sum of squares coil combination (Fig. 1H).

Fig. 1.

Reconstruction flowchart for a data set with MB = 3 and in-plane R = 3. A. Aliased image and its undersampled k-space in PE direction. B. Zero filled k-space in the non-accelerated direction for un-folding aliased slices. C. Reconstructed full k-space with GRAPPA/ARC. D. Single coil un-aliased images. E. K-space of un-aliased slices. F. Full k-space after partial k-space reconstruction with POCS. G. Single coil images after Fermi filtering in k-space. H. Reconstructed images with sum of square coil combination.

2.5.2. SNR calculation and determination of g-factor

Repeated acquisitions of b = 0 (T2 weighted) images from MB1 and MB3 of all 5 volunteers were used to calculate SNR according to Dietrich O et al. (Dietrich et al., 2007). Each slice of the volunteer data was first smoothed with an 8-by-8 mean filter. The SNR was then calculated from Eq. (1) for each voxel within the brain.

$$SNR=\frac{mean\left(voxel\right)}{std\left(voxel\right)}$$ (1)

To calculate g-factor maps, phantom data were used to estimate relative coil sensitivity maps using the eigenvector method described by Walsh et al. (Walsh et al., 2000). g-Factor maps were then estimated from the sensitivity maps with the equation shown in Eq. (2) (Pruessmann et al., 1999) for different under-sampling schemes (MB1, R = 3 and MB3, R = 3).

$$g_j=\sqrt{{\left(C_R^{*}{\mathrm{\Psi }}^{-1}{C}_R\right)}_{j,j}{\left({\left(C_R^{*}{\mathrm{\Psi }}^{-1}{C}_R\right)}^{-1}\right)}_{j,j}}$$ (2)

C_R is the coil sensitivity encoding matrix corresponding to an R fold accelerated acquisition. $\mathrm{\Psi }$ is the noise covariance matrix of the 32-channel coils, which was estimated by calculating the covariate matrix of the noise data acquired with RF excitation disabled.

2.5.3. NODDI and DTI processing

After the multiband data were reconstructed, a susceptibility distortion correction was applied using the TOPUP method available in FSL (Andersson et al., 2003; Smith et al., 2004). Eddy current correction was followed by applying affine registration to a reference volume (eddy_correct, FSL).

The NODDI and DTI models were fitted within the brain mask. The NODDI MATLAB toolbox (http://www.nitrc.org/projects/noddi_toolbox/) was employed for NODDI. In order to fit the NODDI model, the two diffusivities representing the diffusion coefficient of the isotropic compartment (d_iso) and the intrinsic diffusivity of the intra-neurite compartments (d_//) were fixed as in the original model (Zhang et al., 2012) to d_iso = 3.00 µm²/s and d_// = 1.70 µm²/s, which are the values commonly employed in literature for the free diffusivity of water particles in CSF and neural tissue in vivo at body temperature. The DTI fitting program in FSL was employed to fit DTI with weighted least squares tensor fitting (dtifit, FSL). Both models were fitted to the whole double-shell data set, and the DTI model was also applied separately to the shell acquired at b = 1000 s/mm² and a shell acquired at b = 2000 s/mm².

The following voxel-wise maps were obtained. For NODDI: the isotropic volume fraction (v_iso), the intra-neurite (restricted) volume fraction (v_ic), the extra-neurite (hindered) volume fraction (v_ec) and the orientation dispersion index (OD). In this study, we calculated the effective volume fraction for v_ic and v_ec so that v_iso + v_ic + v_ec = 1. For DTI, we evaluated ADC and fractional anisotropy (FA).

3 T anatomical images were rigidly aligned (flirt, FSL) to 7 T diffusion images in order to generate region of interests (ROIs) for the evaluation of NODDI parameters. ROIs included voxels within the region of T2 hyperintensity (T2L) on the FLAIR images and contrast-enhancing lesions (CEL) on the T1-gad images. NAWM, gray matter (GM) and cerebrospinal fluid (CSF) were defined from the 3D SPGR brain images. Median values of diffusion maps were analyzed within each ROI.

2.5.4. Statistical analysis

Statistical analysis was performed using Matlab (Mathworks, Natick, MA). Nonparametric Wilcoxon rank sum tests were applied to assess differences in diffusion maps between tumor grades, or between different regions of interests (ROIs), including T2L, CEL, NAWM, GM and CSF. A p-value of 0.05 or smaller was considered to be significant. Adjustment for multiple comparisons was not applied due to the exploratory nature of this study.

3. Results

3.1. SNR comparison between 3 T and 7 T

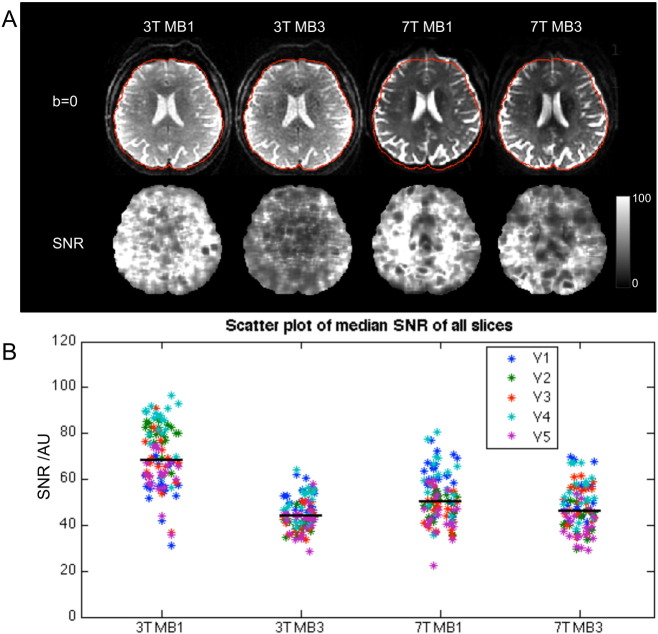
Fig. 2A showed the center slice and the SNR map in a volunteer acquired with MB1 and MB3 at 3 T and 7 T. It can be noted that SNR is less homogeneous at 7 T due to B1 inhomogeneity, and the reduction in SNR from MB1 to MB3 is smaller at 7 T compared to 3 T. The median SNRs of all slices were compared by a scatter plot for all 5 volunteers in Fig. 2B. The median SNR was 68.4 and 43.9 for MB1 and MB3 at 3 T, and 50.2 and 46.1 for MB1 and MB3 at 7 T.

Fig. 2.

A. Center slice and the SNR map of a volunteer acquired with MB1 and MB3 at 3 T and 7 T. It can be noted that SNR is less homogeneous at 7 T due to B1 inhomogeneity, and the reduction in SNR from MB1 to MB3 is smaller at 7 T compared to 3 T. B. Scatter plot of median SNR values of all slices of 5 volunteers (V1–V5). Median SNR of each method was highlighted with a black line, with median SNR = 68.4 and 43.9 for 3 T MB1 and MB3, 50.2 and 46.1 for 7 T MB1 and MB3.

3.2. g-Factor maps

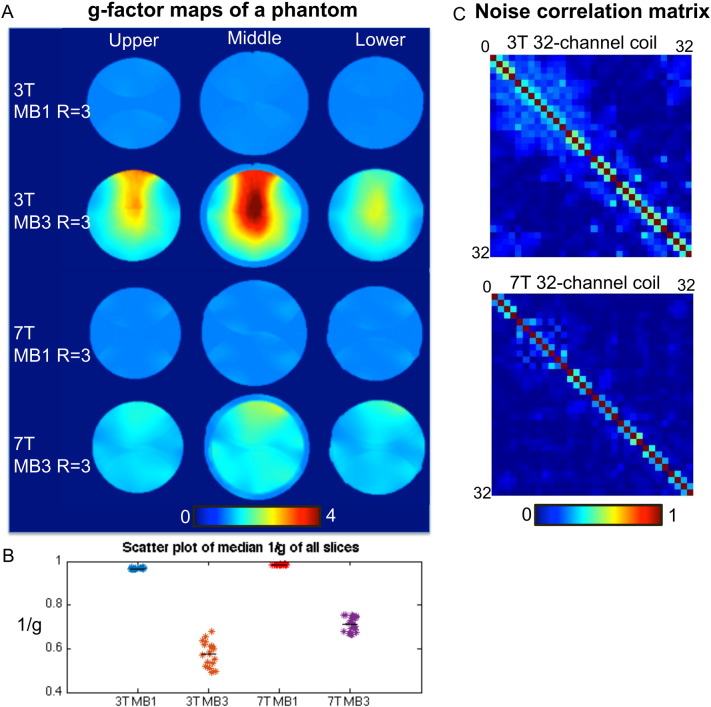
g-Factor maps (center slice and slices 40 mm above and below) at 3 T and 7 T for different undersampling schemes were shown in Fig. 3A. Median 1/g values of all slices were scatter plotted in Fig. 3B, with a black line indicating the median value of each method. Median 1/g was 0.97 and 0.57 for 3 T MB1 and MB3 and 0.98 and 0.71 for 7 T MB1 and MB3. The noise correlation matrix of the 3 T 32-channel coil and 7 T 32-channel coil was shown in Fig. 3C.

Fig. 3.

A. g-Factor maps at 3 T and 7 T when undersampling in one direction (MB1, in-plane, R = 3), or in two directions (MB3, in-plane R = 3). g-Factor maps were calculated from sensitivity maps estimated from a phantom data acquired at different field strengths with 32-channel coils. B. Scatter plot of median 1/g value of all slices. Median 1/g values of each method were shown in black line, with median 1/g = 0.97 and 0.57 for 3 T MB1 and MB3 and 0.98 and 0.71 for 7 T MB1 and MB3.

3.3. DTI and NODDI results in patients

3.3.1. Quality of fit of DTI

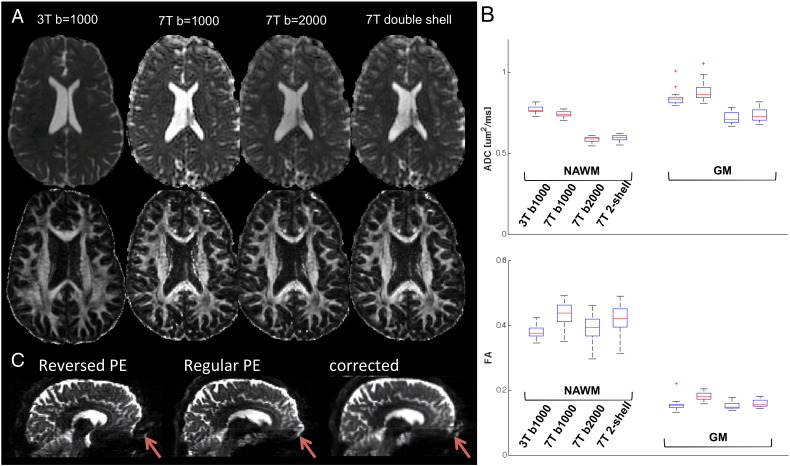
14 out of 20 patients had 3 T DTI data available acquired with a standard sequence. 3 T and 7 T DTI data were compared for this population in their native space, which included: (1) 3 T standard DTI with b = 1000, 24dir; (2) 7 T multiband DTI with b = 1000, 30dir; (3) 7 T multiband DTI with b = 2000, 60dir and (4) 7 T multiband double shell, 90dir. ADC and FA maps of a patient were shown in Fig. 4A. The median values of ADC and FA within NAWM and GM for 14 patients from different data sets are shown with bar plots in Fig. 4B. For b = 1000, the ADC was not significantly different between 3 T and 7 T within the NAWM, and FA was significantly higher at 7 T (p < 0.0001). As expected, the ADC obtained at b = 2000 was significantly lower than ADC at b = 1000 (p < 0.0001) due to the non-Gaussianity of water diffusion in a restricted environment, and the values fitted from the double shell were in between the values fitted from each shell.

Fig. 4.

A. ADC and FA maps for patient data acquired with (1) 3 T standard DTI, b = 1000, 24dir; (2) 7 T multiband, b = 1000, 30dir; (3) 7 T multiband, b = 2000, 60dir and (4) 7 T multiband, double shell. B. Box plots of median ADC and FA within NAWM, GM of 14 patients. C. Susceptibility artifact correction with TOPUP for a patient data set that was acquired with multiband at 7 T.

Correction for susceptibility artifacts with TOPUP is shown in Fig. 4C for a patient data set that was acquired at 7 T. It can be seen that distortions were in the opposite direction between reversed and regular phase encoding blips, and with TOPUP the distortion was well corrected.

3.3.2. Evaluation of NODDI parameters

The mean and standard deviation of NODDI and DTI parameters in the NAWM, GM, CSF, T2L and CEL were summarized in Table 3, as a function of tumor grade. Within both the T2L and CEL, the ADC was significantly higher and FA was lower than in NAWM (p < 0.0001). Both v_iso and v_ec were significantly elevated (p < 0.0001) compared to NAWM and v_ic was significantly decreased (p < 0.0001). ADC was significantly lower in the CEL than the T2L, while OD and Vic were significantly higher (p < 0.01, p < 0.001), v_iso was significantly lower (p < 0.05) and v_ec was not significantly different between the two lesions. These metrics were not found to be different between tumor grades (p > 0.1).

Table 3.

DTI and NODDI matrix values (mean ± SD) in the T2L, CEL, NAWM, GM and CSF.

	T2L	CEL	NAWM	GM	CSF
	N = 20	N = 11	N = 20	N = 20	N = 20
ADC	1.29 ± 0.21	0.97 ± 0.19	0.61 ± 0.03	0.79 ± 0.05	1.41 ± 0.20
FA	0.17 ± 0.04	0.17 ± 0.04	0.36 ± 0.05	0.15 ± 0.01	0.09 ± 0.02
OD	0.25 ± 0.08	0.35 ± 0.09	0.29 ± 0.03	0.46 ± 0.03	0.46 ± 0.03
viso	0.37 ± 0.19	0.15 ± 0.12	0.09 ± 0.05	0.11 ± 0.08	0.66 ± 0.19
vic	0.16 ± 0.08	0.32 ± 0.17	0.55 ± 0.06	0.38 ± 0.04	0.13 ± 0.07
vec	0.43 ± 0.15	0.44 ± 0.21	0.28 ± 0.06	0.34 ± 0.08	0.07 ± 0.10

	G2 T2L	G3 T2L	G4 T2L	G2 CEL	G3 CEL	G4 CEL
	N = 10	N = 3	N = 7	N = 5	N = 1	N = 5
ADC	1.27 ± 0.20	1.43 ± 0.22	1.24 ± 0.21	0.99 ± 0.25	1.05 ± 0.00	0.94 ± 0.16
FA	0.18 ± 0.04	0.13 ± 0.02	0.16 ± 0.04	0.18 ± 0.03	0.11 ± 0.00	0.18 ± 0.04
OD	0.23 ± 0.07	0.26 ± 0.10	0.28 ± 0.08	0.34 ± 0.08	0.44 ± 0.00	0.34 ± 0.11
viso	0.36 ± 0.21	0.43 ± 0.23	0.35 ± 0.17	0.15 ± 0.10	0.41 ± 0.00	0.10 ± 0.10
vic	0.15 ± 0.06	0.11 ± 0.05	0.19 ± 0.10	0.30 ± 0.24	0.24 ± 0.00	0.35 ± 0.12
vec	0.46 ± 0.16	0.42 ± 0.19	0.39 ± 0.14	0.44 ± 0.26	0.34 ± 0.00	0.47 ± 0.19

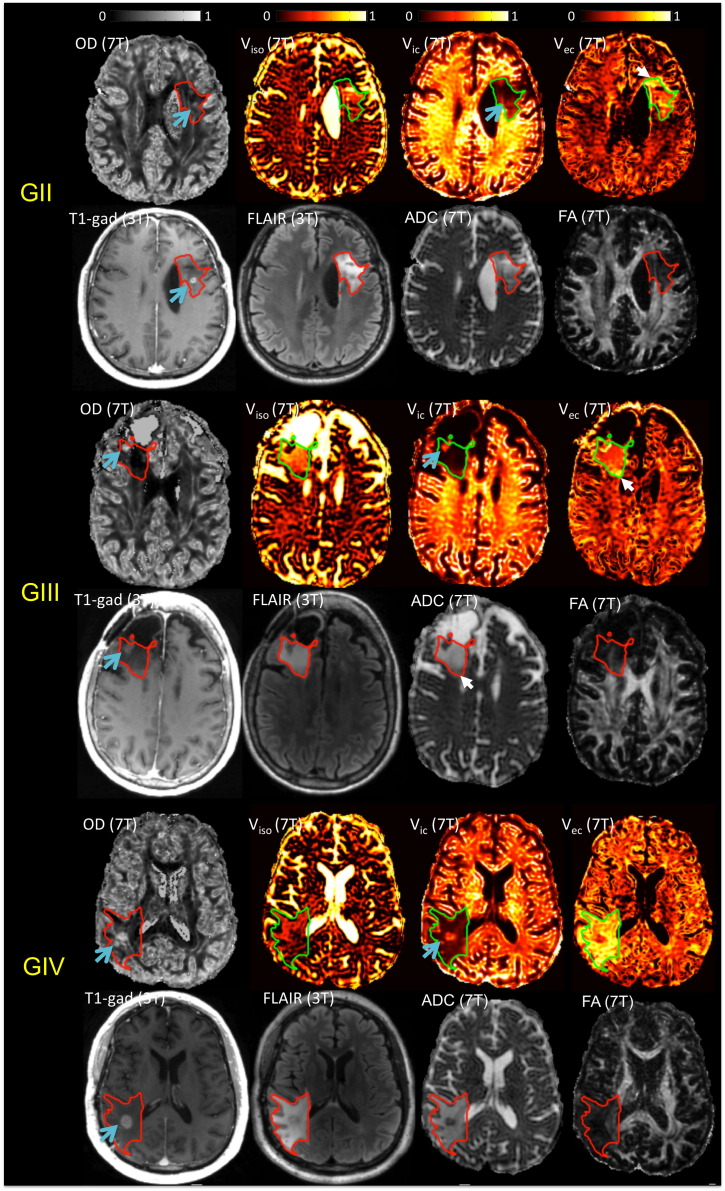
NODDI maps of three patients who had lesions with different grades are shown in Fig. 5, together with ADC and FA maps fitted from the same double-shell data, and 3 T T1-gad and FLAIR images. All three patients had received radiation therapy (RT) and were stable at the time of scan. Within in the T2L, variations were seen in v_iso, v_ic and v_ec, that reflected different water mobility characteristics. Contrast enhancing lesions were present in all patients (blue arrow) and all demonstrated elevated OD and v_ic compared to surrounding tissues. The white arrow indicates two interesting regions at the edge of T2L of the grade II and grade III patients. These regions could easily be missed on anatomical images and DTI maps, as their intensities were very close to NAWM, but were highlighted in NODDI maps due to elevated v_ec.

Fig. 5.

NODDI maps of three patients with lesions of different grades, together with ADC and FA maps fitted from the same double-shell data, and 3 T T1-gad and FLAIR images. T2L was outlined, defined as the hyperintensity abnormality in the FLAIR image. Within in the T2L, variations were seen in v_iso, v_ic, and v_ec, reflecting different water mobility characteristics at different parts of the lesion. Contrast enhancing lesions were present in all patients (arrow) and all demonstrated elevated OD and v_ic. The white arrow indicated two interesting regions at the edge of T2L of the grade II and grade III patients, which could easily be easily missed on anatomical images and DTI maps, but was highlighted due to elevated v_ec.

4. Discussion

The use of sophisticated diffusion models to provide improved characterization of tissue composition is a promising technique for evaluating lesion heterogeneity in patients with glioma. The application of these models has typically been limited by the need to acquire a large number of diffusion directions at high b-values which is not feasible in clinical settings (Assaf and Basser, 2005; Panagiotaki et al., 2014). In this study, we demonstrated the feasibility of acquiring multishell diffusion weighted data in the whole brain using the multiband technique within the same acquisition time that has been used to acquire routine DTI. The resulting data were fitted with both NODDI and standard DTI models. Our results showed that the NODDI maps were able to provide unique contrast within the T2L and are likely to provide information that is complementary to FA and ADC.

Major concerns for obtaining diffusion data using ultra high field strength MR scanners are increased variation in B0 and B1. In this study, we used 3-fold in-plane acceleration to shorten TE, as well as to increase the bandwidth in the phase-encoding direction in order to reduce the extent of distortion. To further correct for the susceptibility distortion, we used the TOPUP correction by adding an additional b = 0 image with reversed phase encoding blips into the sequence (Andersson et al., 2003; Smith et al., 2004). The correction performed well for these data, as was illustrated in Fig. 4C. B1 inhomogeneity caused spin-echo imperfections over the entire brain, resulting in non-uniform signal intensity. To ameliorate this situation, we optimized the transmitter gain based on the median B1 of the image volume by incorporating the measured B1 field strength. It has been previously demonstrated that this technique can improve the situation by providing 82% of the available spin echo signal (D. Kelley, 2013). The volunteer data in Fig. 2 illustrate uniform images from central slice.

The performance of the EPI sequence at ultra-high field has been difficult to assess because the T2 values of brain tissue are difficult to measure accurately at 7 T. We carried out a straightforward SNR comparison between 3 T and 7 T with the same hardware settings (gradient, coils) and acquisition parameters (TR, TE, k-space coverage and voxel size). Our results showed that without multiband, the SNR was higher at 3 T (SNR ≈ 68.4) than 7 T (SNR ≈ 50.2), indicating that the shortened T2 as well as increased B0 and B1 inhomogeneity at 7 T outweighed the increased static magnetization and the total signal was reduced at the same echo time. However, when 3-fold acceleration was applied with multiband, the SNR was comparable between 3 T (SNR ≈ 43.9) and 7 T (SNR ≈ 46.1). The SNR loss after simultaneous multi-slice acquisition is caused by the spatially dependent amplification of noise, known as the geometry factor, or ‘g-factor’. Our estimation of g-factor maps showed that with MB = 3 and in-plane R = 3, the g-factor was lower at 7 T (g = 1.4) than 3 T (g = 1.75). This explained why SNR is no longer superior at 3 T with a multiband factor of 3. The improved g-factor map at 7 T compared to 3 T that was observed in our study is in great agreement with the literature (Wiesinger et al., 2004b). It has been shown both in theory (Kelley et al., 2008; Ohliger et al., 2003; Wiesinger et al., 2004a) and in experiments (Kelley et al., 2008; Wiesinger et al., 2004b) that the g-factor is dependent upon B₀ field strength at high field (B₀ > 1.5 T), and improves as the field increases, because the coil sensitivities grow progressively asymmetric (Collins et al., 2002) and become increasingly structured due to the shortening RF wavelength and related interference effects (Yang et al., 2002). It has also been demonstrated that improvement in the g-factor at high field becomes more obvious as acceleration factor increases (Wiesinger et al., 2004b). Our data demonstrated comparable SNR between 7 T and 3 T with 9-fold acceleration, and it can be predicted that a higher acceleration factor can be achieved at 7 T with less reduction in SNR compared to 3 T.

The multiband diffusion sequence was applied to the characterization of glioma using a 2-shell, 90-direction protocol that is straightforward to implement and sufficiently economical for clinical applications, yet sophisticated enough to distinguish three types of water diffusion in the brain. The ADC and FA maps fitted from this 7 T protocol were first compared to the data acquired at 3 T for patients with both data sets available (N = 14). Our results showed that ADC values at b = 1000 mm²/s within NAWM and GM were close between 3 T and 7 T, with ADC higher in GM than NAWM, which is consistent with the trend reported in the literature (Helenius et al., 2002). FA values were higher at 7 T in both NAWM and GM, which could be caused by the difference in SNR between the two acquisitions, with a lower SNR at 7 T (MB3, SNR ≈ 46.1/33 dB) than 3 T (standard DTI, SNR > 68.4/37 dB). Increasing FA with decreasing SNR has been reported in both experiments and computer simulations. Pierpaoli et al. (Pierpaoli et al., 1996) showed that, for lower SNR, the longitudinal principal eigenvalue λ1 was overestimated, whereas the eigenvalues λ2/λ3 are underestimated, leading to overestimation of FA. Landman et al. (Landman et al., 2007) developed a theoretical framework to model the influence of noise in DTI and showed that for SNR < 40 dB in b = 0 s/mm² images, mean FA increased with decreasing SNR, and ADC was less affected than FA. Out results for FA and ADC were both supportive of these findings.

The NODDI model distinguishes three types of water diffusion behavior and each was quantified with a compartment fraction. When applied to tumor, it is natural to speculate that vasogenic edema would belong to v_iso given its isotropically fast diffusing movement. Invading tumor cells along fiber tracts should be categorized as v_ec, as they co-exist with glial cells in the space around the neurites. Our data were supportive of these assumptions by showing increased v_iso and decreased v_ic within T2L and CEL lesions compared to NAWM, consistent with increased edema and loss of neurons. The increased v_ec was likely to reflect the invading tumor cells. These assumptions should be validated with tissue samples, which were not available in the current study. Patients recruited into this study were at different stages of disease and had received varying treatments, which may explain why these matrices were not found to be significantly different between tumor grades.

The NODDI maps provided unique contrast across the tumor and highlighted interesting regions that could not be seen in ADC or FA maps. The different types of contrast observed may be reflective of progressive disease or of treatment effects that are worth noting for radiologists. Obtaining follow-up data at later time points would be valuable for tracking changes in these regions and may be helpful in interpreting them. Definitive verification and interpretation would require the use of image guided tissue samples and will be considered for future studies.

Another interesting finding that is observed in Fig. 5 was that v_ic values were higher in CEL compared to the T2L. In the NODDI model, v_ic represents neuron density, which conflicts with this finding as we know that the CEL contains less neurons than T2L and reflects either the most aggressive tumor packed with dense tumor cells or non-specific changes related to treatment effect. This suggests that when applied to tumor, v_ic can no longer be interpreted as “neuron density”. Rather, the elevated v_ic can be explained by the presence of restrictive structures with restrictions in all direction, which is consistent with the similarly elevated OD. This warned us that we should be very cautious when interpreting NODDI results in tumor, as this model was not directly built on tumor and some parameters were prefixed based on values in normal brain such as the intrinsic free diffusivity in v_ic.

The 3-fold acceleration in the slice direction was the highest that could be obtained with our current multiband technique, as the separation of aliased slices (40 mm) is close to the coil size and SNR lost would be exacerbated if a higher acceleration factor was used in that direction. Another technique, termed blipped-CAIPIRINHA can be implemented to both increase the SNR and achieve a higher acceleration factor (Setsompop et al., 2012). This technique can reduce the g-factor in simultaneous multi-slice acquisitions by introducing interslice image shifts and thus increase the distance between aliased voxels. Another limitation was that we used the Shinnar–Le Roux (SLR) optimized RF pulses where the high RF energy transmission limited the optimal TR that can be achieved at high field due to specific absorption rate (SAR). Advanced RF pulse design techniques have been reported to lower the peak RF power at ultra high field (Eichner et al., 2014; Sharma et al., 2015). Implementation of these techniques will further improve SNR and reduce the acquisition time. These will be considered for future studies.

In conclusion, we have demonstrated the feasibility of using multiband diffusion weighted imaging at 7 T within 6 min in order to apply the NODDI model to characterizing glioma. The 7 T diffusion data quality was generally comparable to data acquired at 3 T and quantitative diffusion measurements (ADC and FA) were similar. Anatomical imaging at 7 T benefits from the higher SNR, and the ability to consistently obtain high quality diffusion data at 7 T will contribute towards the implementation of a comprehensive brain MRI examination at ultra-high field. We have shown that NODDI maps provided unique contrast within the T2L lesion that was not seen in anatomical images or DTI maps. Such contrast may reflect the complexity of tissue compositions associated with disease progression and treatment effects. Changes in v_iso, v_ic and v_ec in tumor lesions compared with NAWM were consistent with the alternations in tissue components within tumor. Histological analysis of image-guided tissue samples is needed in future studies to better understand these variations.