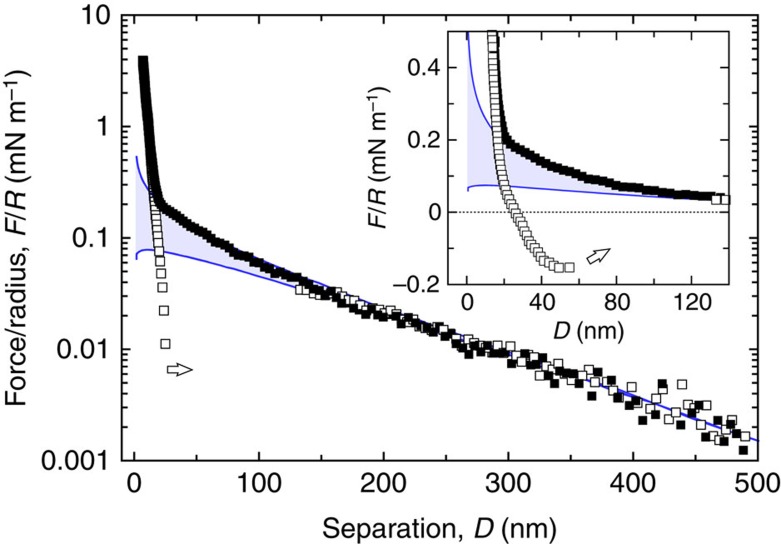
Figure 4. Total surface forces.

Measured forces, F, normalized by the mean radius of curvature of the surfaces, R, between the functionalized bilayers of Fig. 1, as a function of surface separation, D. Solid symbols (▪) describe forces on approach and open symbols (□) the corresponding forces on separation. The upper and lower solid lines are fits from a DLVO model34,35 with, respectively, a constant surface charge σ₀ or a constant surface potential Ψ₀ boundary conditions (best fit gives σ₀=28 μC m⁻²; Ψ₀=44 mV). The electrostatic component of the DLVO model is computed from numerical solutions of the nonlinear Poisson–Boltzmann equation36 and the attractive van der Waals force is obtained with a calculated non-retarded Hamaker constant A₁₂₁=1 × 10⁻²⁰ J using the Lifshitz theory37. Note that the DLVO fit is constrained by the long-range exponential nature of the force profile at large separation distances, with a Debye screening length κ⁻¹=110 nm. At small separations the force–distance profile deviates significantly from the predicted electrostatic repulsion due to the compression of the STL brush. Furthermore, at such strong compressions, the forces acquire an irreversible component and eventually a pull-off force must be applied to wrench the surfaces apart (arrows), as better seen in the linear scale plot of the inset.