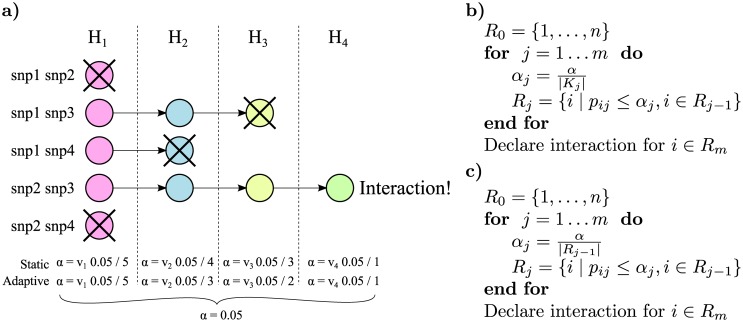
Fig 1. Illustration of the rejection procedure.

a) We have a set of four hypotheses that are closed under intersection. We start at stage 1 by testing the simplest null hypothesis H ₁ for each variant pair; the p-value threshold α for this test is corrected for the total number of pairs. In the figure H ₁ is accepted in the first and last pair, and these pairs will not be tested in the subsequent stages. We then continue through the null hypotheses from simple to complex but correcting the α for each stage only for the expected number of pairs, in the static method, or the actual number of pairs, in the adaptive method, that are tested at this stage. Finally if all null hypotheses could be rejected for a specific pair i (e.g., snp2 and snp3 in the figure), we declare pair i to be interacting. b) Pseudocode describing the static stage-wise testing method. Variant pairs are ordered from 1 to n. Null hypotheses are ordered from 1 to m in any order that respects the partial order of how they are nested. Only pairs for which the null hypothesis was rejected in the previous step are considered in the current step. The p-value for testing null hypothesis j for pair i is p _ij. Rejected hypotheses in stage j are contained in the set R _j, and α is the significance threshold. The hypotheses of interaction for pair i is accepted only if the null hypotheses for all m tests could be rejected. c) Pseudocode describing the adaptive method. The overall algorithm is the same as the static. However, the significance threshold is now determined by the total number of rejections in the previous stage ∣R _j−1∣.