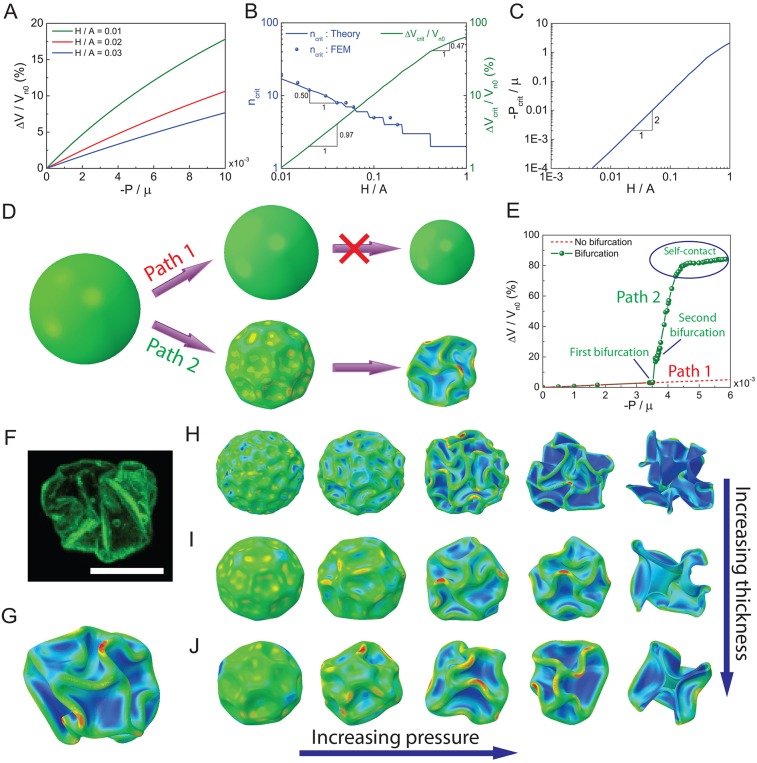
Fig. 7.
Model calculations of nuclear deformation and wrinkling. We model the nuclear envelope as an elastic shell with shear modulus μ. (A) Volumetric reduction under compressive pressure from homogeneous deformation for nuclei with different thickness-to-radius ratios (H/A; Eqn 2). The volume decreases with increasing compressive pressure. (B) With increasing pressure, the nuclear envelope buckles at a critical mode number, ncrit. This critical mode number and volume reduction depend on H/A. The theoretical results are compared to the numerical simulations using the FEM. (C) Dependence of the critical pressure at the onset of buckling on H/A. (D) Shape of the nucleus with increasing compressive pressure. Path 1 shows homogeneous deformation where the nucleus maintains spherical geometry. Path 2 contains two successive buckling transitions. The first buckling (bifurcation) transition develops regular dimples or polygons paving the nuclear surface. These regular buckling patterns are distorted by the second buckling transition, generating a folded structure. (E) Nuclear volume shrinkage with increasing compressive pressure. Path 1 and 2 are obtained from theoretical analysis and FEM simulation, respectively. (F) Confocal image of a fully buckled nucleus in an MEF cell after complete detachment. Scale bar: 10 μm. (G) Folded nucleus produced by FEM simulation. The thickness-to-radius ratio here is H/A≈0.027, which appears to match the experimental image. (H–J) FEM simulations of nuclei shape as a function of increasing compressive pressure with thickness-to-radius ratios (H/A) of 0.01, 0.027 and 0.05, respectively. The last column is a cross-section of a folded nucleus.