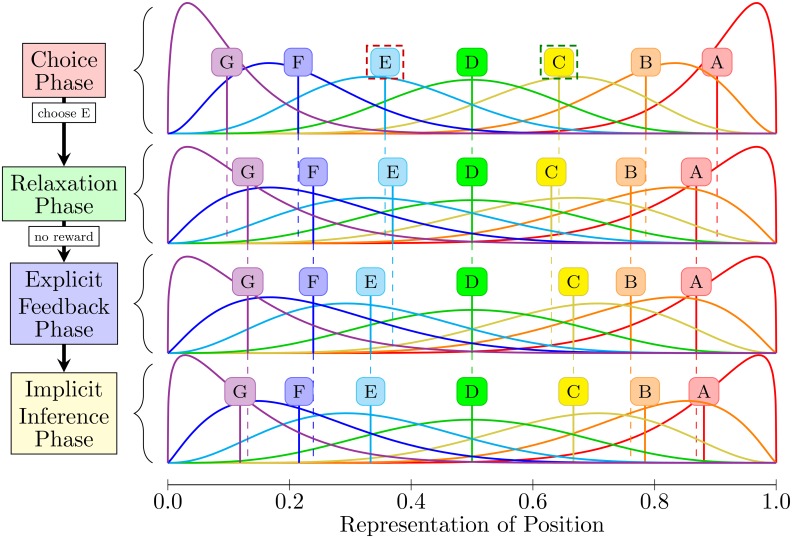
Fig 3. Visualization of Betasort’s adjustment of the beta distributions during a single trial in which an incorrect response is given.

For this example, the trial stimuli are the pair CE. The initial conditions show the beta distributions of a well-learned list, with means marked by a vertical line. During the choice phase, a value is drawn randomly from the beta distributions of each trial stimulus, and the stimulus with the larger random value is chosen. In this example, the algorithm incorrectly selects stimulus E, an unlikely but possible event. Immediately following the choice, but before feedback is taken into account, the positions of all stimuli are relaxed (using ξ = 0.6 for this example). This has the effect of making all density functions slightly more uniform, and reduces the influence of older trials in favor of more recent ones. During explicit feedback, the increases L _E by one, while also increasing U _C by one. This increases the odds of future selections of stimulus C, while decreasing the odds of future selections of stimulus E. Next, the algorithm makes implicit inferences about the positions of all known stimuli that did not appear during the trial. Because stimulus D falls between C and E, its count of successes and failures is consolidated and its position does not change. Stimuli A and B are positioned above the trial stimuli, and so are shifted upward. Stimuli F and G are shifted downward.