Viewpoint: Unresolved mysteries

in an editorial in the March 2012 issue of the Journal of Applied Physiology, Nieman (11) highlighted a topic that has simmered below the surface for decades, i.e., how does the lung acinus expand with lung inflation. Indeed, the topic may be the last frontier of gross anatomy, but it is one that is sufficiently important in lung health and disease that it warrants a more prominent status. The potential models of acinar expansion were nicely discussed over 25 years ago by Greaves et al. (6), and the schematic drawings of the different expansion modes illustrated in Fig. 1 are derived from this paper.

Fig. 1.

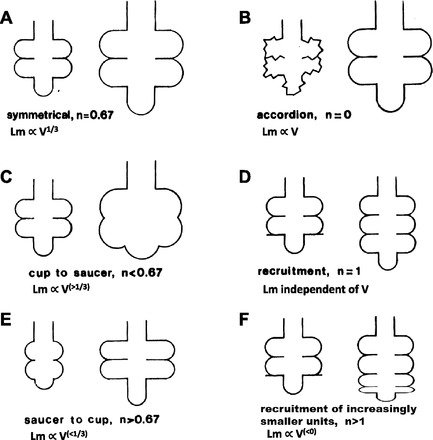
Models illustrating how surface area and linear intercept (Lm) may change with increasing lung volume. The n is the exponent on lung volume (V) reflecting how surface area (S) changes (S∝Vⁿ). Because Lm equals 4V/S (3), we also have added the relation between Lm and V. [Figure modified with permission from Greaves et al. (6).]

Most of the 19th and 20th century studies addressing this issue relied on lungs fixed at a single inflation, so even if all the problems associated with fixation, tissue processing, and interpreting three-dimensional (3D) structure from two-dimensional sections were resolved, the effect of changes at a different inflation level could still only be evaluated by looking at a different set of lungs. However, in the 21st century, modern imaging technology has advanced to the point where there is now hope that it may soon be possible to actually visualize the effects of lung inflation on 3D terminal lung structure (8, 10, 12, 15). Unfortunately, we are not yet there, so our understanding must still rely on the existing data. In an attempt to address this question, Hajari et al. (7) presented a sophisticated analysis of lung structural changes using diffusion MRI of hyperpolarized ³He. This method allows quantification of an apparent diffusion coefficient (ADC), which is approximately proportional to the mean diffusional displacement of ³He in three dimensions and is a parameter related to the mean linear intercept, Lm (9, 19). Hajari et al. went a step further and fitted their MRI data to a conceptual model of an alveolar duct. The results led to some provocative conclusions about how the lung structure changes with inflation, specifically that alveoli are recruited during lung inflation, but that this occurs with no change in internal surface area. However, the validity of these conclusions depends on adjusting the parameters of a model of a single alveolar duct (or many such randomly oriented ducts within the imaging space) to fit the data. In addition, an intact lung consists of many mechanically interdependent cylinders, that would likely result in increasing dimensional variability with lung inflation. Such variability in a 3D space-filling lung places limits on the ability of this simple model to assess lung structural dimensions as the lung inflates.

Alternatively, it is possible to estimate the 1D Lm in vivo with few assumptions by quantifying the settling of a monodisperse aerosol in alveoli and ducts. The settling rate in the gravitational field is constant, so the number of particles remaining airborne after a defined breath hold is directly related to the Lm. Using this aerosol method (16), we have found results that partially support the work of Hajari et al. (7). With inflation from a degassed state, particle deposition increased, which indicates that the mean Lm in the lung steadily decreased. This recruitment occurred at all volumes up to our defined total lung capacity. These results would be consistent with the calculated increase in alveolar number found by Hajari et al. (7) if the alveoli recruited later were increasingly smaller, but not consistent with their finding of an unchanging alveolar surface area with increasing lung volume. Their result is consistent with recruitment of alveoli of equivalent size. In addition, we also showed that once the lung was inflated, on deflation, there was no change in Lm. Because surface area is a function of the ratio of parenchymal volume to Lm, this result would suggest that on deflation there is a continuous fall in surface area. So these aerosol data are not consistent with the constant surface area data obtained with the hyperpolarized helium or the model proposed. It is also important to note that another group using ³He to measure ADC (but not the modeling done by Hajari et al.) has reported a decrease in ADC as the lung is inflated and interpreted the results by assuming alveolar recruitment (4).

Any workable model of alveolar geometry should be able to account for the pressure-volume behavior during inflation and deflation. Our aerosol data are also supported by observations related to pressure-volume hysteresis, something not examined by Hajari et al. We showed that in situ changes in mean linear intercept could provide insight into the differences between inflation and deflation. Our results parallel those reported by Radford (13, 14). He visualized subpleural alveoli during inflation and deflation, and his direct observations of decreasing airspace dimensions with inflation and a constant airspace diameter with deflation are strikingly similar to our quantitative measurements of airspace size using aerosol deposition. In humans, in vivo aerosol measurements of mean linear intercept in normal and diseased patients have also correlated well with PFT data (2) and with CT imaging (1). It is not easy to account for differences in these data and in the proposed model and explanations of Hajari et al. (7), because changes in the lung with inflation could affect both methods differently.

The different possibilities for acinar expansion are schematically illustrated in Fig. 1. Internal parenchymal surface area (S) is shown to vary with lung volume (V) raised to the nth power for the different conditions shown. We have added to the original figure, a new image in Fig. 1F, consistent with the aerosol deposition data. Because Lm equals 4V/S (3), for each inflation model, we have also added the equations showing how Lm will change with V. If there were a shortening of alveolar depth with inflation (Fig. 1C) as concluded by Hajari et al. (7), then this should have led to an increased settling time and increased Lm. This is what is in fact implied by the results from Hajari et al, but not from the results reported by Cereda et al. (4). Were there opposite changes in the duct, such that with inflation there was an increased alveolar depth [Fig. 1E; as was suggested by Radford (14)], this could be consistent with the aerosol data, but not with an increased number of alveoli. As noted by Greaves et al. (5), however, the insights gained from power law equations in such complex geometries may be quite limited. Further complicating the discrepancies with these in vivo measurements are unambiguous results from postmortem measurements of frozen lungs (5, 17, 18), which have been interpreted as showing isotropic expansion of all alveoli with lung inflation (Fig. 1A), a conclusion that is inconsistent with both the MRI modeling of hyperpolarized ³He and aerosol deposition data. Thus, although the mystery of Amelia Earhart may have been resolved (11), what happens to lung acinar structure with lung inflation in a pathologic or even in a normal healthy lung remains unresolved.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the authors.

AUTHOR CONTRIBUTIONS

Author contributions: G.C.S. and W.M. conception and design of research; G.C.S. and W.M. performed experiments; G.C.S. and W.M. analyzed data; G.C.S. and W.M. interpreted results of experiments; G.C.S. and W.M. prepared figures; G.C.S. and W.M. drafted manuscript; G.C.S. and W.M. edited and revised manuscript; G.C.S. and W.M. approved final version of manuscript.