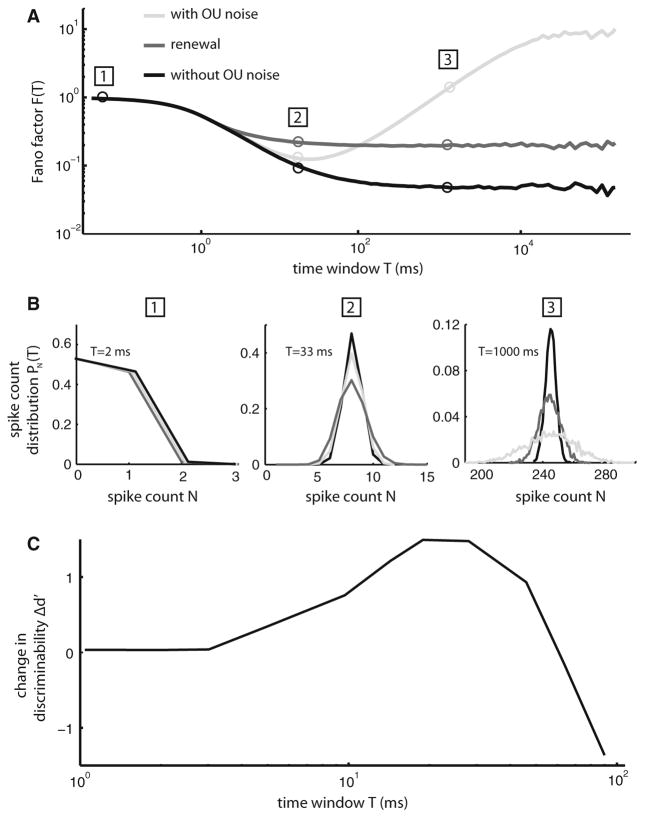
Fig. 5.

Positive and negative ISI correlations act to create a minimum in spike train variability for a given time window T. a Fano factor F(T) from the LIFDT neuron model driven by a weak Ornstein–Uhlenbeck (OU) noise with a long correlation time (light gray). Also shown are the Fano factor F(T) computed from the same model without the OU noise (black) and after shuffling the ISI sequence (dark gray). b Spike count distributions PN(T) obtained for all three conditions. For T = 2 ms (left), the distributions show almost complete overlap. However, for T = 33 ms (middle), the spike count distribution obtained from the LIFDT model without OU noise (black) shows the weakest variance, followed by the distribution obtained with the model with OU noise (light gray), followed by the distribution obtained after shuffling. However, for T = 1,000 ms (right), it is the distribution obtained from the model with OU noise (light gray) that has the highest variance. c Change in discriminability measure d′ (i.e. the difference between d′ computed from the model with OU noise and d′ computed after shuffling the ISI sequence) as a function of the time window length T. It is seen that the gain in discriminability is maximal for a value of T for which the Fano factor F(T) is minimum