Fig. 2.

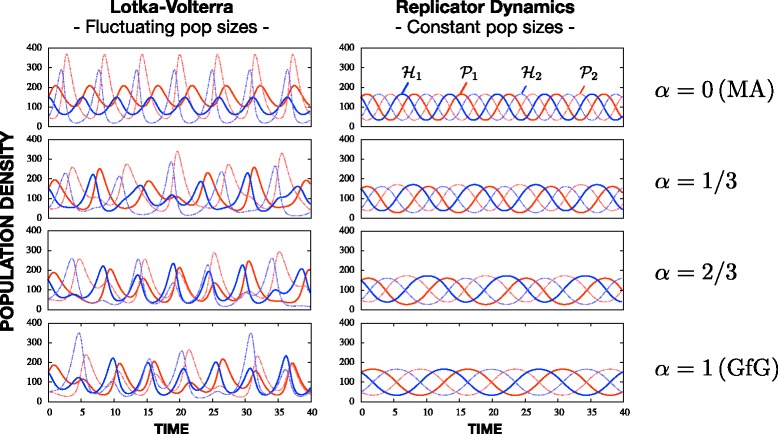
Example of population dynamics based on the Lotka-Volterra equations (left) and the Replicator Dynamics (right). While the dynamics on the right side resembles the common Red Queen pattern, the left side is more complex. In a pure matching-allele model (top), the plot on the left shows two independent sets of Lotka-Volterra dynamics, one for ${\mathcal{\mathscr{H}}}_1$ and ${\mathcal{P}}_1$ (blue and red solid lines, correspondingly) and a second one for ${\mathcal{\mathscr{H}}}_2$ and ${\mathcal{P}}_2$ (blue and red dotted lines). As the model deviates from MA model with increasing α (rows 2–4) more complicated dynamics arise, since the four population densities of ${\mathcal{\mathscr{H}}}_1$, ${\mathcal{\mathscr{H}}}_2$, ${\mathcal{P}}_1$, and ${\mathcal{P}}_2$ are coupled (parameters γ=0.005, κ=0.5, and σ=0.01 for both Lotka-Volterra and Replicator Dynamics. Host birth rate b _h=1.5 and parasite death rate d _p=1.0 in the Lotka-Volterra case. Initial population densities h ₁=p ₁=150, h ₂=p ₂=50)