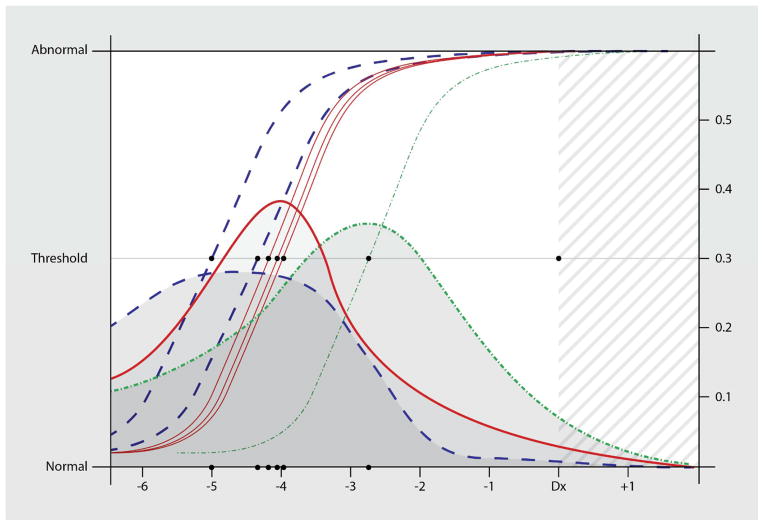
Figure 1.

Logistic curves (left-side Y-axis scale) represent the predicted clinical thresholds for decline on each of the subtests sensitive to disease onset. These thresholds are the models’ average departure from the stable state to the active disease state in participants who eventually develop PDD. They are derived from the probability densities (right-side Y-axis scale) which represent the cumulative distributions of these models’ estimated time-of- onset for the active disease state (changepoint). In this figure we have convolved the subtests’ distributions to indicate the 3 proposed epochs. These epochs are based on our previous longitudinal factor analysis using this sample. Standard errors reflect the sensitivity/specificity of the subtests to detect change (slope of the logistic curves measured at the threshold).

Epoch I – Working Memory (Long Dashed Lines)

• (a)
  Digit Span - Backwards Subtest of the WMS
• (b)
  Mental Control Subtest of the WMS

Epoch II – Visuospatial Processing (Solid Lines)

• (c)
  Digit Symbol Substitution Subtest of the WMS
• (d)
  Block Design Subtest of the WAIS
• (e)
  Benton Visual Retention Test – Copy

Epoch II – Semantic Memory (Short Dashed Lines)

• (f)
  Information Subtest of the WMS

Model Specification. Let Y_ij represent the j^th measurement time of the i^th individual. The models considered assumed that the Y_ij were distributed normally with expectation E[Y_ij] and variance ${\sigma }_{ij}^2$. The two phases were modeled as linear fixed-effects with slopes β₁, β₂. The transition between the phases is continuous at an individual’s changepoint, δ_i. δ_i was modeled as a random effect. The fixed-effect intercept (α) is interpreted as the level of the specific measurement at the changepoint. All parameters were assumed to be independent. Standard uninformative priors were chosen for the fixed effects and for the priors and hyper-priors of the random effects.

$$\begin{array}{l}{Y}_{ij}~N(E[Y_{ij}],{\sigma }_{ij}^2)\\ E[Y_{ij}]=\{\begin{array}{cc}\alpha +{\beta }_1(t_{ij}-{\delta }_i)& t_{ij}<{\delta }_i\\ \alpha +{\beta }_2(t_{ij}-{\delta }_i)& t_{ij}\ge {\delta }_i\end{array}\end{array}$$

Parameter Specification:

• α, β₁, β₂ ~ N (0,1000)
• δ_i ~ N(μ_i, τ_i)
• μ_i ~ N (0,1000) < 0
• τ_i ~ Gamma (0.001,0.001)
• ${\sigma }_{ij}^2~\mathit{Gamma}(0.001,0.001)$