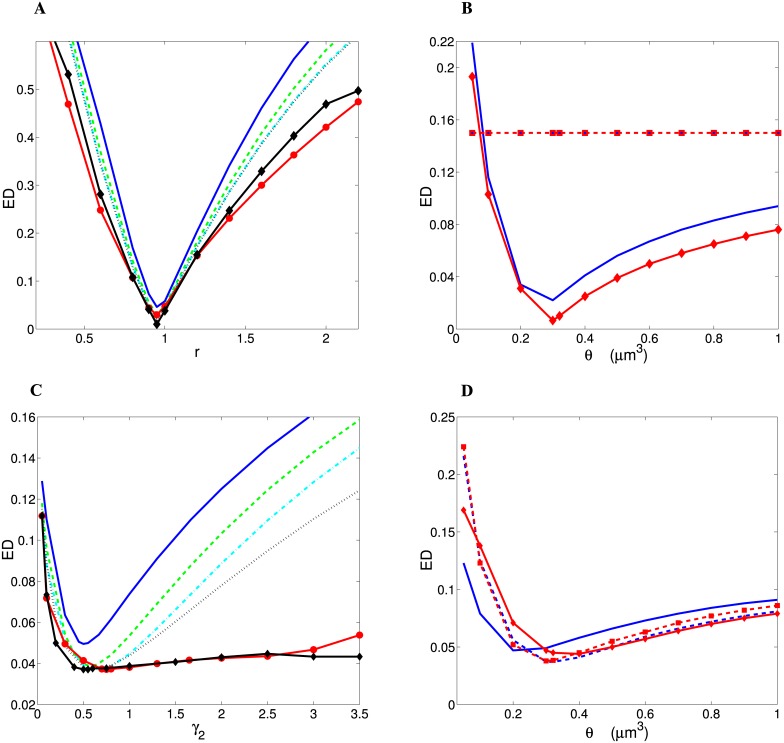
Fig 5. Euclidean distance (ED) between optimal theoretical results and empirical data as a function of r, threshold θ, and γ ₁, γ ₂.

Panels (A) and (B) refer to “wire minimization”, whereas panels (C) and (D) correspond to “spine economical maximization”. (A) Dependence of ED on r for all distributions of spine volumes for “wire volume minimization”, i.e. γ ₁ = 0. (B) ED as a function θ for r = 0.95. Blue lines correspond to Gamma (n = 2) distribution and red lines (with diamonds and squares) to Log-normal (γ ₁ = 0 for solid lines and γ ₁ = 0.65 for dashed lines). For Log-normal distribution σ = 0.3. Note that for γ ₁ > 0 ED is constant (dashed red line with blue squares), i.e. ED = 0.15. (C) Dependence of ED on γ ₂ for all distributions of spine volumes. (D) ED as a function θ. Blue lines correspond to Gamma (n = 2) distribution and red lines (with diamonds and squares) to Log-normal (γ ₂ = 0.3 for solid lines and γ ₂ = 0.65 for dashed lines). For Log-normal distribution σ = 0.25. In panels (A) and (C) θ = 0.321 μm³, and the following labels were used: Exponential distribution is shown as solid blue line, Gamma (n = 1) and Gamma (n = 2) are shown respectively as dashed green and dashdot cyan lines, Rayleigh distribution is represented by dotted black line, Log-logistic is shown as solid red line with circles, and Log-normal as solid black line with diamonds. The curves for Log-logistic and Log-normal correspond to different values of the parameters, respectively, β and σ that yield the minimal ED for a given r or γ ₂.