Figure 10. Modifying the countermanding model .

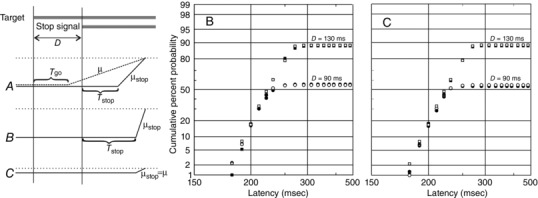
In the original model, there is a race between a Go unit and a Stop unit, which starts after a delay D; both have the same fixed delay T _go = T _stop, although μ_stop is greater than μ_go, such that the Stop process frequently overtakes the Go (A, left), with the decision signal reaching the threshold level (dotted line) sooner. Estimates of μ_stop in countermanding are smaller than we have observed for the Wheeless task, although the original countermanding behaviour can be accurately simulated with the increased value for μ_stop if T _stop is increased as well, relative to T _go. The results of such a simulation are presented in reciprobit plot B, which shows uncancelled responses in countermanding trials, with ΔT = 0 (filled symbols: μ_stop = 13.8 Hz, σ_stop = 3.0 Hz) and ΔT = +26 ms (open symbols: μ_stop = 24.0 Hz, σ_stop = 5.0 Hz). Simulations are shown for D = 90 ms and D = 130 ms; for all cases, μ = 6.11 Hz, σ = 1.05 Hz and T _go = 60 ms. Each simulation is of 1,000 trials, and the distributions for each value of D are not significantly different (P > 0.5, K–S 2). Furthermore, by assuming a reduced threshold level for the stop process (C, left), the values of μ and σ for the Stop unit can be the same as for the Go unit. Reciprobit plot C compares simulated reaction times, as in B, for the original model and for one in which μ_stop = μ_go and σ_stop = σ_go: the distributions are again statistically indistinguishable (P > 0.5, K–S 2).