Review of photoacoustic flow imaging: its current state and its promises

Abstract

Flow imaging is an important method for quantification in many medical imaging modalities, with applications ranging from estimating wall shear rate to detecting angiogenesis. Modalities like ultrasound and optical coherence tomography both offer flow imaging capabilities, but suffer from low contrast to red blood cells and are sensitive to clutter artefacts. Photoacoustic imaging (PAI) is a relatively new field, with a recent interest in flow imaging. The recent enthusiasm for PA flow imaging is due to its intrinsic contrast to haemoglobin, which offers a new spin on existing methods of flow imaging, and some unique approaches in addition. This review article will delve into the research on photoacoustic flow imaging, explain the principles behind the many techniques and comment on their individual advantages and disadvantages.

1. Introduction

Blood flow in arteries, veins and smaller capillaries is an important aspect in the diagnosis of a wide range of pathologies and diseases. Blood flow can be estimated with either flow imaging or perfusion imaging, and both provide distinct and valuable information. Flow imaging is the process of mapping where functional vascularity is, or what the flow profile is within an artery or vein. The latter can be used for estimating, for example, the wall shear rate [1] or detecting where turbulent blood flow occurs [2,3]. Imaging vascularity is important to reveal for example angiogenesis [4], the process during which rapid growth of new vasculature occurs. The resulting vasculature, irregularly and haphazardly shaped, is the pathological result of for instance tumour growth [5] and inflammatory diseases such as rheumatoid arthritis [6].

Perfusion imaging is related to flow imaging, but provides a more global picture of vascularity, that describes how much blood reaches organs, muscles or skin over time [7]. The amount of skin perfusion determines for instance the chance of a burn healing [8], and in cerebral ischemia, malperfusion of parts of the brain leads potentially to stroke [9]. The perfusion can be visualised as the integration of flow speed over the total cross sectional area of the feeding vasculature [10]. Perfusion and the amount of flow imaged are therefore closely related in some clinical applications, however, computing the perfusion from imaged vascularity is often challenging [11].

Photoacoustic imaging has the potential to do both: perfusion imaging and flow imaging. In this review we will only focus on the latter. A wide variety of methods investigated by different research groups, inspired by other imaging modalities, in addition to a few approaches that utilise unique aspects of photoacoustic imaging, make the review a worthwhile investigation. We will first briefly discuss existing imaging modalities that are capable of both perfusion imaging and flow imaging before describing the different photoacoustic approaches developed so far.

1.1. Current modalities

Magnetic resonance imaging (MRI) is a widely used modality for imaging perfusion and flow, using a range of methods [12,13]. For instance, imaging flow can be performed using phase contrast MRI [14], while perfusion imaging can be done with arterial spin labelling [15] or dynamic contrast enhanced imaging [16]. MRI can provide blood flow information of the whole body, with high sensitivity and resolution [17], which makes it unique in that aspect. Moreover, it can be combined with blood-oxygenation-level dependent (BOLD) MRI [18]. However, MRI is very expensive in both the initial investment and the upkeep, and the extensive pulsing schemes in MRI also make imaging a slow process [19].

Dynamic contrast enhanced computed tomography (CT) is a more affordable modality for perfusion imaging, unlike MRI. It can also be combined with positron emission tomography (PET) for quantification of e.g. glucose consumption for estimation of the complete metabolic activity [20]. Like MRI, CT is also capable of imaging complete organs or even the whole body, but with worse resolution and it relies on ionizing radiation, making it unpractical for monitoring [19].

Ultrasound (US) imaging is another widely used technique for both flow and perfusion imaging. Over several decades, the ultrasound community has developed many techniques. For instance, flow imaging can be performed using continuous wave excitation in spectral Doppler US [21], by imaging phase change of reflected US pulses in colour flow imaging [22] or by transverse speckle tracking [23]. Perfusion imaging is performed using dynamic contrast enhanced US, for example by using a flash-replenishment technique [24]. US imaging is very scalable through the inverse relationship of penetration depth and resolution, which can be tuned using the ultrasound emission frequency and bandwidth [25]. Furthermore, US imaging is both affordable and portable [26]. While imaging depth is larger than optical coherence tomography, the resolution is poorer and it suffers from clutter [27].

Several modalities are being developed to estimate flow and perfusion using visible or infrared light, which makes these techniques both harmless and affordable. For example, laser Doppler perfusion imaging (LDPI) and laser speckle imaging (LSI) are two modalities based on tracking diffusely reflected light over time and can be used for perfusion imaging of the skin [28], with the advantages of portability, low cost and real-time imaging [29,30]. On the other hand, LDPI and LSI are limited to superficial imaging and low resolution [28] and do not feature depth resolution. While LDPI has the objective underlying principle of velocity related Doppler shifts, quantifying perfusion in an absolute manner remains challenging in both LDPI and LSI because of the unknown optical properties of the tissue [31]. Another optical technique, orthogonal polarization spectral imaging (OPS), can be used for high-resolution imaging of micro-vasculature [32]. Resolution is high and penetration depth is fair, but flow quantification is very challenging.

Optical coherence tomography (OCT) is an optical technique which can be used for flow imaging as a function of depth [33]. Flow can be quantified, for instance, by tracking the phase change of the reflected light over time, or by computing the speckle variance [34]. OCT has high resolution, is depth resolved and can be portable, but suffers from limited penetration depth and is hindered by clutter [35].

In this regard PAI is comparable to fluorescence microscopy approaches like confocal microscopy [36] or the two-photon variant [37]. In both microscopy techniques flow imaging is performed by laser scanning along the flow direction. However, confocal and two-photon require fluorescent markers that are susceptible to photobleaching; are only useable in superficial applications; and the laser scanning makes it only suitable for imaging a few blood vessels at a time [38]. As we will see, photoacoustics can be used to overcome these problems in flow imaging. Photoacoustic flow imaging, uses endogenous contrast, and allows approaches not limited to specific targeting of blood vessels.

1.2. The case for PA flow imaging

Photoacoustic imaging (PAI) is an optical modality that relies on light pulses to generate ultrasound at locations of high optical absorption [39]. Nanosecond light pulses are directed onto the skin, where they diffuse through tissue, down to several centimetres for near-infrared light. The light is locally absorbed by tissue chromophores, and is converted into heat, causing a pressure build-up. This build-up is released in the form of pressure waves: sound waves very similar to those emitted in pulse-echo ultrasound.

The main tissue chromophores in the visible and near infrared wavelengths (NIR) are haemoglobin and melanin (<1000 nm); at NIR wavelengths (>930 nm) lipids also exhibit absorption peaks that can be utilized [40]. PAI can therefore be used spectroscopically and, using spectral unmixing, the relative concentrations of chromophores can be extracted [41]. In this way, the oxygenation of blood vessels can be determined by exploiting the oxygenation-dependent absorption spectrum of haemoglobin [42,43].

Like ultrasound imaging, PAI is relatively low cost, can be used in portable devices [44], and the resolution can be increased relatively easily though at the cost of imaging depth. PAI is used in microscopy, tomography and linear array systems, with varying resolutions and imaging depths [45]. An important distinction in systems can be made, namely between acoustic and optical resolution setups. In optical resolution mode, laser light is focussed onto a sample; in acoustic resolution mode, generated sound waves are focussed in detection with a large numerical aperture–either physically or in computed reconstruction. The focal size determines the lateral resolution. The optical focus therefore gives a higher resolution, but at the cost of penetration depth: optical scattering will broaden the optical focus considerably. It should be noted that in both cases the axial resolution–along the ultrasound transducer axis–remains governed by the acoustic bandwidth of the transducer.

The promise of using photoacoustics for imaging flow is due to its reliance on absorption for contrast, as opposed to backscattered waves in US and OCT. Moreover, because of the relatively low concentration of haemoglobin and other chromophores in tissue, there is a high contrast in PAI between vasculature and the surrounding tissue [46]. In addition, PAI–unlike ultrasound–is relatively speckle free [47,48]. The lack of these two properties is the main reason it is challenging to detect flow in small blood vessels and near vessel walls with OCT and US flow imaging [49–51].

In the following review, we present a summary of the research performed on photoacoustic flow imaging. We describe the similarities between some flow imaging methods using PA with other modalities, and conclude with the key advantages and unique features of PA flow imaging. The review is partly written as a tutorial on the various flow imaging techniques, but it will also go into detail on performance characteristics like the minimum and maximum measureable velocities.

2. Photoacoustic flow imaging methods

2.1. Doppler shift

2.1.1. Continuous-wave photoacoustic Doppler

Fang et al. proposed a technique where the Doppler shift of a PA modulation was estimated [52], similar to what is done with spectral Doppler US. The authors used a diode laser that was intensity modulated with a frequency $f_0$:

$$I\left(t\right)=\frac{I_0}{2}\left[1+\cos \left(2\pi f_{0}t\right)\right]$$

with $t$ the time within one acquisition, $I_0$ and $I\left(t\right)$ the maximum and time-variant light intensity respectively. A modulated laser will generate a PA response that is also oscillating with frequency $f_0$ (see Fig. 1). If excited red blood cells (RBCs) are flowing at $v_{flow}$, then the particles will emit a PA response that is Doppler shifted approximated by:

$$\Delta f=f_0\frac{v_{flow}}{v_s}\cos \theta$$

with $\theta$ the angle between the flow direction and the detector's viewing line, and $v_s$ the speed of sound. They implemented the technique on an acoustic resolution setup with a ∼2.5 MHz focussed mono-element transducer and a lock-in amplifier for detection; the modulation was matched to this frequency. Fang et al. measured a distribution of Doppler shifts–not a single value–due to spectral broadening, caused by the opening angle of the ultrasonic transducer and the presence of a distribution of velocities in the tubing.

Fig. 1.

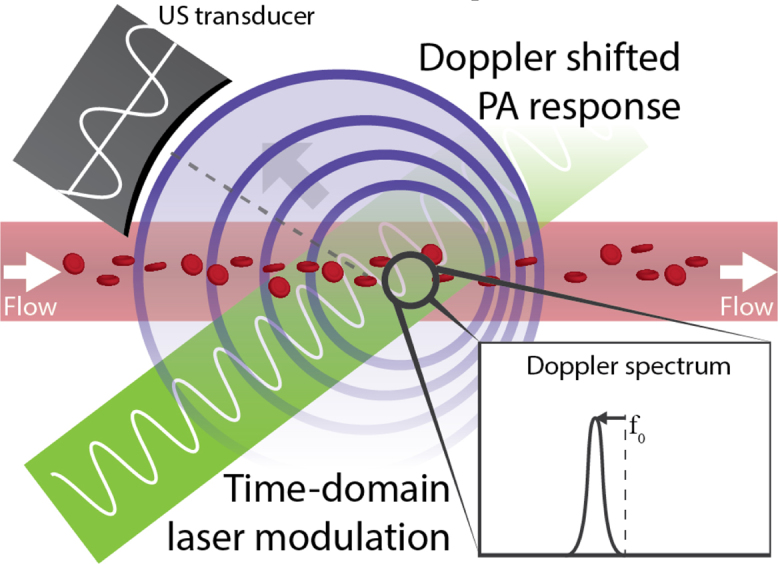
In continuous-wave photoacoustic Doppler, sinusoidal modulation of the excitation light source causes a photoacoustic response, which is Doppler shifted if absorbing particles or cells are flowing.

The authors demonstrated the technique on flowing carbon particles, which served as a model for RBCs. In their first paper they measured velocities of flowing carbon particles through tubing, which ranged from 0.055 to 8.8 mm/s. With their technique, the minimum measureable velocity was fundamentally limited by the frequency resolution (=1/acquisition time) of the system, whereas the maximum measureable velocity was limited by the system's SNR: for greater flow velocities the distribution of Doppler shifts broadened, and therefore the amplitude decreased.

In a second study they used a more realistic phantom where they included also scattering (${\mu }_s^{\text{'}}=0.4/\text{cm}$, path length 3 cm) and increased the density of carbon particles from 15% to 40% (v/v) [53]. The maximum measureable velocity dropped to 1 mm/s due to the scattering, which reduced the SNR; but measurements seemed unaffected by the increased particle concentration. The authors indicated blood measurements were successful, but only in water, without any scattering.

Sheinfeld et al. followed up on this work and improved the axial resolution using short bursts of modulated light [54,55]. They used rectangular bursts with intensity

$$I\left(t\right)=\frac{I_0}{2}\left[1+\cos \left(2\pi f_{0}t\right)\right]{\displaystyle \sum }_{n=1}^{N}rect\left(\frac{t-n{T}_{rep}}{T_{on}}\right)$$

where $T_{rep}$ and $T_{on}$ are the repetition interval and cycle length respectively, of burst number $n$.

They used an acoustic resolution setup with a 1 MHz transducer to detect the Doppler shift from the PA responses of flowing carbon particles (in their case in a 10% (v/v) suspension). They applied a time gate to the time traces and estimated the Doppler shift in a 3 μs window for a range of positions. The size of time gate determined the axial resolution, which therefore was 4.5 mm. Their 1 s acquisition length was long enough to detect multiple bursts, so the time gate was repeated every $T_{\text{rep}}=70\mu s$ to increase the spectral resolution.

The authors measured velocities from 3.5 to 203 mm/s; in their case the maximum speed was limited by the syringe pump, the minimum–as before–by the spectral resolution.

For both Sheinfeld et al. and Fang et al., the lateral resolution was determined by the ultrasound transducer's beam width. Speculating on the maximum penetration depth; it is expected to be fairly limited. In fact, Fang et al., found imaging through scattering (${\mu }_s^{\text{'}}=0.4/\text{cm}$ with a 3 cm path length) challenging in spite of using highly absorbing carbon particles and much lower optical scattering than in tissue (${\mu }_s^{\text{'}}\approx 8/\text{cm}$). For an overview of the technique's key attributes, see Table 1 at the end of the review article. In this table, the flow imaging techniques yet to be discussed will be listed also.

Table 1.

Summary of the attributes of photoacoustic flow imaging techniques. * indicates alternative resolution (acoustic/optical) might be usable, but has not been demonstrated yet.

	Method	Calibration required?	Meas. quantity	Flow axis	Resolution limit
					Lateral	Axial
Doppler shift
Continuous-wave (Sec. 2.1.1)	Fourier transform	No	Velocity spectrum	Axial	Acoustic*	#Cycles
Structured-illumination (Sec. 2.1.2)		No		Either	#Fringes	Acoustic
Density tracking
Time-domain (Sec. 2.2.1)	Cross correlation	No	Velocity	Axial	Acoustic or optical	Acoustic
Spatial domain (Sec. 2.2.2)		No		Lateral	Distance between foci	Acoustic
Transit time
Single-particles (Sec. 2.3.1)	FWHM	Yes	Speed	Lateral	Optical*	Acoustic
Particle ensembles (Sec. 2.3.2)	Autocorrelation or bandwidth	Yes	Velocity	Lateral	Optical*	Acoustic
Amplitude encoding
Contrast based (Sec. 2.4.1)	Contrast inflow	Yes	Speed	Any	Acoustic*	Acoustic
Heat encoding (Sec. 2.4.2)	Heated spot	No	Velocity	Any	Heating spot	Acoustic

2.1.2. Structured-illumination photoacoustic Doppler

Zhang et al. implemented photoacoustic modulation in the spatial domain instead of time domain by creating illumination fringes with a nanosecond pulsed laser [56]. The modulation frequency corresponds to $f_0=v_s/d$, with a fringe pitch of $d$; and the Doppler shift of the PA modulation as before: $\Delta f=f_0\frac{v_{flow}}{v_s}\cos \theta$

Since their detection geometry was parallel to the modulation–as can be seen in Fig. 2–the Doppler angle was $\theta =0^{\circ }$.

Fig. 2.

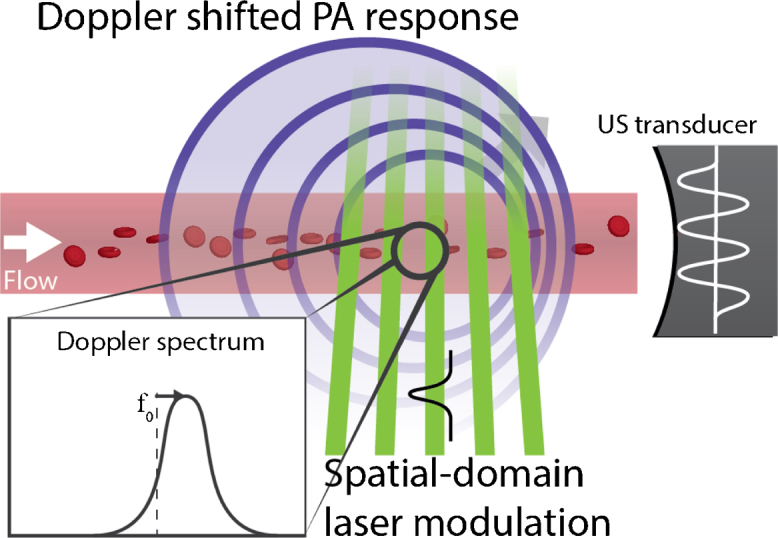
Using spatial laser modulation in structured-illumination photoacoustic Doppler causes a modulation of the PA response similarly to the time-domain version, and the modulation is likewise Doppler shifted under flow.

They estimated not only the Doppler shift, but also related quantities, namely the phase shift, the change in arrival time and time compression of the photoacoustic response. In their experiments they used an ink solution with flow speeds from 20 mm/s to 1400 mm/s. When the authors added optical scattering (${\mu }_s^{\text{'}}=6.2/\text{cm}$) they measured up to ∼600 mm/s. Zhang et al. found the time compression to give the best accuracy compared to the Doppler shift (Root-mean-square error, RMSE of 57 mm/s instead of 89 mm/s), especially with optical scattering (RMSE = 66 mm/s instead of 120 mm/s). Note that time compression is inversely related to bandwidth broadening: it seems likely that their flow setup shows a wide distribution of flow speeds, and therefore high amount of broadening.

The minimum and maximum measureable velocities were determined, as before, by the frequency resolution and the SNR respectively. The authors achieved a much higher SNR by using a pulsed laser–compared to CW modulation–which explains the high maximum measureable velocity.

Optical scattering decreases the modulation depth and therefore decreases the SNR of the Doppler shift. This makes spatial modulation more suited for flow estimation with superficial applications like photoacoustic microscopy. The lateral resolution would then be determined by the length of the fringe pattern; the resolution in depth would be very limited because the ultrasound transducer is used to determine flow component along the transducer time-axis.

Yao et al. presented a method using a microscopy setup with spatial light modulation to estimate the transverse flow component–which is perpendicular to the transducer's symmetry axis–instead of the axial component [57]. Modulation was performed using a laser fringe pattern:

$$I\left(x\right)\propto 1+a\cos \left(\frac{2\pi x}{d}\right)$$

with $a$ the modulation depth and $x$ the transverse axis. They recorded $p\left(n{T}_{rep}\right)$, the maximum of each photoacoustic response sampled at each excitation pulse $n$, also called the ‘slow-time response’. It is termed such to distinguish it from the fast-time response that is the result of an individual laser pulse, of which Zhang et al computed the Doppler shift. Yao et al.’s fast-time response was a representation of the particle density distribution that flowed through the fringe pattern, and the amplitude of any photoacoustic response was proportional to the number of particles within one fringe. This density distribution ‘finger print’ is deterministic and changes slowly over time. As the particle distribution flowed from fringe to fringe, an amplitude modulation was created in the slow-time response (see Fig. 3), which could be observed as side bands at $\pm 2\pi v_x/d$. They assumed the particles to have no correlation length and therefore a flat spatial frequency spectrum.

Fig. 3.

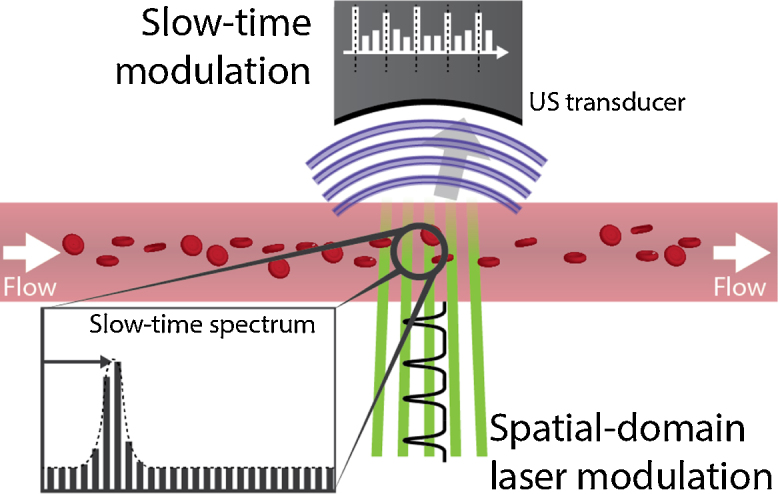
In the transverse structured-illumination method, the PA response as the cells or particles move through the fringes gets modulated with a frequency based on their flow speed.

Yao et al. first demonstrated the method by flowing bovine blood through tubing and for various (< 10 μm) particle sizes with flow speeds ranging from 5 to 20 mm/s. The authors also showed the radial flow profile of the flow in the tubing. They also demonstrated their method in the superficial vasculature of a mouse ear, where they measured a flow speed of approximately 1.9 mm/s.

The theoretical minimum measureable speed in the system was 0.01 mm/s, limited by the total acquisition time of 1 s. Their maximum measureable speed was ∼25 mm/s, limited in their case by the combination of fringe spacing and laser pulse repetition frequency (PRF), since the density distribution requires adequate sampling in time. The lateral resolution was limited by the size of the acoustic focus, about 71 μm and the axial resolution at ∼15 μm by the bandwidth of the ultrasound transducer.

Note that both spatial-modulation techniques only measure one lateral flow component at a time, and that no directionality is included; the latter might be possible by scanning the system back and forth. Also, a second scan could be made to determine the other lateral flow component.

2.2. Density tracking

2.2.1. Cross-correlation flow imaging in the time domain

Brunker and Beard used two pulsed lasers to excite particles with a small time delay in between, such that the time-of-flight could be extracted [58]. They use the fact that the density distribution of particles or RBCs can also be sampled along the transducer axis (the ‘fast-time response’). If the transducer is aligned along the particle flow then the distribution will move toward or away from the transducer–depending on the flow direction (see Fig. 4). This also holds when the transducer is aligned at an angle $\theta (\ne 90°)$ to the flow: the particles within the measurement volume will shift along the detection-time axis. During the two laser pulses the density distribution shifted along the detection time by $\Delta t$ in the fast-time response. This time shift could be estimated using a cross-correlation, and the axial velocity could then be estimated with:

$$v_{axial}=\frac{v_s\Delta t}{T_p\cos \left(\theta \right)}$$

with $T_p$ the time between the two laser pulses. The method is similar to how ultrasonic colour flow imaging works (CFI, also termed ‘Colour Doppler’), where the back scattering amplitude of ultrasound is linked to the particle density. In CFI the flow estimation is often performed with a two-dimensional autocorrelation, since the imaging is at a constant PRF (the reader is referred to [22] for more information).

Fig. 4.

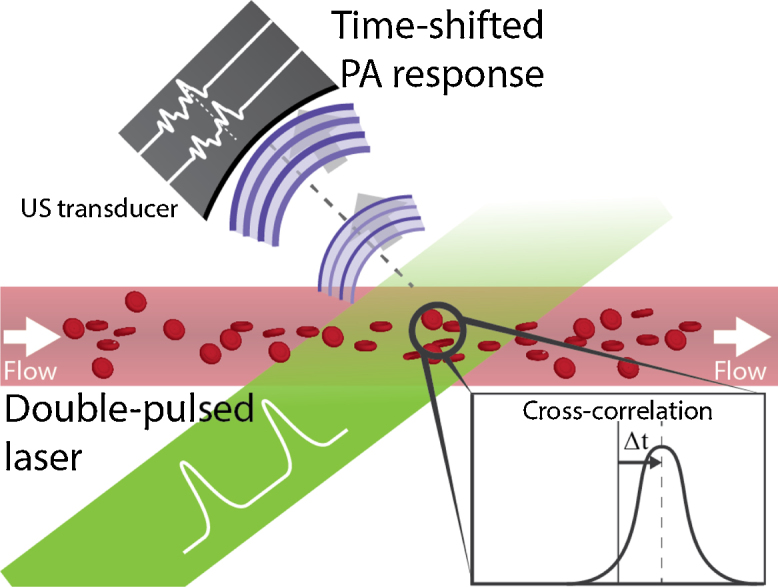
In time-domain cross-correlation flow imaging, the cells’ or particles’ density distribution is interrogated with two consecutive laser pulses. The PA response of these two pulses is shifted in time due to flow.

Brunker and Beard demonstrated the method on a rotating Perspex disk with an acetate sheet imprinted with a random dotted pattern. The rotation of these dots would simulate the flow of red blood cells. The authors initially used two individually triggered 10 Hz pulsed lasers to interrogate the random dotted pattern on the rotating disk. They measured velocities up to 1 m/s, with a systematic error of 1-3% and a random error of 0.02-0.05 m/s.

Brunker et al. later used a double-pulse laser, which provided 2 pulses per 10 Hz, and applied the method successfully to flowing particles and whole blood [59]. Here, they used time gating on the sampled density distribution to estimate the maximum velocity in the tubing. With whole blood the maximum measureable velocity was 20 mm/s and the random error ∼5 mm/s.

The minimum measureable velocity was limited by the precision of the time shift estimation. While this estimation can be performed sub-sample–interpolating or fitting the cross-correlation with a Gaussian function–it is fundamentally limited by the SNR. In addition, the degree of correlation between two subsequent PA responses and the transducer bandwidth also affect the precision. The fundamental lowest possible random error in delay estimation is described in ultrasound colour flow imaging by the Cramer Rao lower bound [60]:

$${\sigma }_{\Delta t}\ge \sqrt{\frac{3}{2f_0^3{\pi }^{2}T\left(B^3+12B\right)}\left(\frac{1}{{\rho }^2}{\left(1+\frac{1}{SN{R}^2}\right)}^2-1\right)}$$

with $T$ the window length of the time gate, $\rho$ the correlation coefficient of the two photoacoustic responses, $f_0$ the centre frequency and $B$ the fractional bandwidth.

The maximum measureable velocity in their rotating disk experiments was limited by the size of the transducer focus and $T_p$, because the dots had to be in the detection area for both laser pulses. On blood, their measurements at higher flow velocities were limited by decorrelation of the density distribution between the two laser pulses. In theory also aliasing might play a role, but this was not observed with the rotating disk, and it is expected at higher velocities than the authors could measure with blood. The axial resolution was determined by the size of the time gate; the lateral resolution by the size of the transducer focus.

Their setup would be limited in penetration depth to < 1 mm due to the use of 532 nm excitation (limited light penetration in tissue and blood), and the use of a 30 MHz transducer (high ultrasound attenuation in tissue). Nevertheless, there is no fundamental reason which prevents the technique from being used in a tomography or linear array system. This would also enable the estimation of the angle $\theta$, which in its current form would require scanning the mono-element transducer.

Yao et al. implemented a similar method using an optical resolution photoacoustic microscope (OR-PAM) [61]. Instead of computing the cross-correlation of two consecutive photoacoustic time traces, they estimated the phase shift $\Delta \varphi$ to determine the axial flow velocity:

$$v_{axial}=\frac{1}{2\pi }\frac{v_s\Delta \varphi }{f_0}$$

They validated the technique on blood flow in tubing, where they could measure flow velocities from 0.1 mm/s to 8 mm/s. Their theoretical maximum measureable velocity was 20 mm/s, limited by the width of their optical focus.

They combined the axial velocity estimation with a transverse method based on bandwidth broadening (see section 2.3.2). In this way they could estimate the total flow velocity and determine the Doppler angle; then scanning the optical focus allowed them to perform flow mapping as shown in Fig. 5.

Fig. 5.

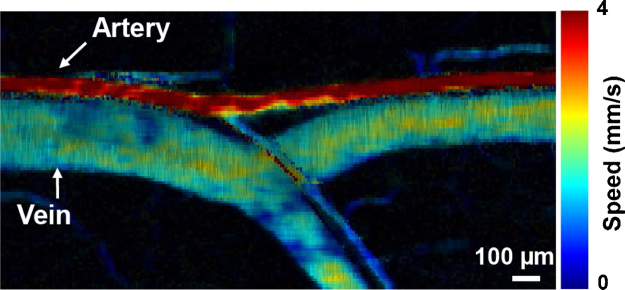
In-vivo example of flow mapping using a scanned photoacoustic microscope. Adapted with permission from [61]. Copyright (2012) by Sage Publications.

Song et al. applied this method with a laser scanning photoacoustic microscope (LS-PAM) [62]. In LS-PAM, an unfocussed ultrasound transducer is kept static, while the optical focus is scanned within the field of view of the transducer. From a scan line along tubing they used the depth information to estimate the flow angle $\theta$.

2.2.2. Cross-correlation flow imaging in the spatial domain

Liang et al. implemented cross-correlation flow imaging in the spatial-domain by projecting an image of a digital micro-mirror device (DMD) onto a sample using an objective [63]. The DMD was programmed to provide photoacoustic excitation at two locations, a certain distance $d$ apart. By switching the DMD pattern, the excitation locations could be alternated, thereby sampling the density distributions at either location separately (see Fig. 6). The time-shift $\Delta T$ between the two slow-time responses over successive laser pulses could be used to estimate the transverse flow velocity:

$$v_{trans}=\frac{d}{\Delta T\sin \left(\theta \right)}$$

Fig. 6.

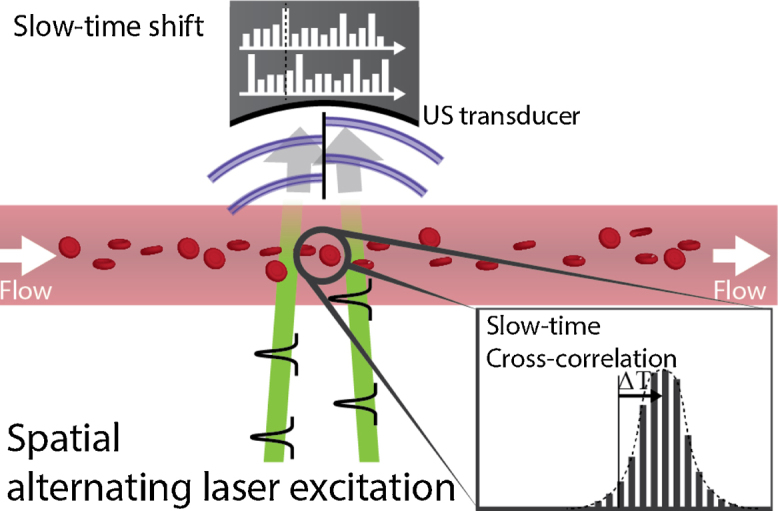
Principle behind spatial-domain cross-correlation flow imaging [63,64]. The density distribution is interrogated at two locations over with alternating laser pulses. The time-shift between the two slow-time responses is determined by the flow velocity.

They demonstrated the technique using various particle sizes (5, 10, 15 μm) and they showed the flow measuring performance is fairly independent of these particle sizes. Measureable flow velocities were from 1.13 to 13.20 mm/s when 300 μm of chicken breast was placed on top of the tubing. The systematic error in their latter experiments was ∼0.29 mm/s and their random error ∼0.19 mm/s. The same group demonstrated the technique with blood-flow in a different publication [64]. They showed measureable velocities of bovine blood flowing through tubing from 0.45 mm/s to 18 mm/s. Several examples of flow estimation in-vivo with mouse ear vasculature were also shown.

In theory the maximum measureable velocity was limited through $\left|v_{\max }\right|=d/T_{rep}$, but this limit was not reached. It seems likely that their measurements were limited by decorrelation of the density distribution, comparable to what Brunker et al. observed. As was the case with other methods, the minimum measureable velocity was limited by the accuracy of the errors in estimating the time-shift $\Delta T$. Implemented as a ‘point’ evaluation, the measurements did not take long (100 ms), but when scanned in 2D the technique would perhaps be on the slow side.

The axial resolution was limited as before by the transducer bandwidth; the lateral resolution along the flow direction was determined by the distance between the excitation spots; the lateral resolution across the flow direction was determined by the spot size.

Wang et al. developed a related technique [65]. They used PA microscopy with repeating line scanning along a vessel in a mouse ear to image individual RBCs in the vessel. By repeatedly scanning the vessel they could image the movement of these cells over time and could use this to quantify the flow velocity. They combined the flow velocity with the oxygenation to model the rate of oxygen release. The technique was also used by Yao et al. to determine the effect of sensory input on blood flow in mouse brains [66].

2.3. Transit time

2.3.1. Transit-time flow imaging of single-particles

Fang and Wang used a PAM, but in optical resolution mode to estimate the transit time of particles flowing through the optical focus [67]. This transit time, when combined with the size of the focus provided an estimation for the lateral flow velocity as can be seen in Fig. 7. Since the slow-time response as the particle transits the focus was a convolution of the optical intensity profile and the particle size, it needed compensation for the size of the particles. They approximated the response by a Gaussian function with a waist equal to the sum of the focal and particle sizes, and fitted the measured data using this approximation.

Fig. 7.

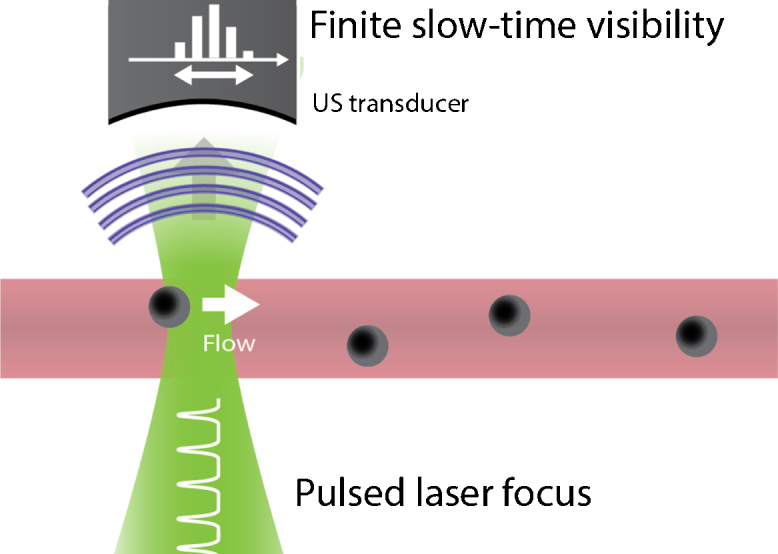
Transit-time flow imaging principle for single particles [67,68]: the time during which a cell or a particle is visible is determined by the speed at which it transits the optical focus.

They showed a parabolic flow profile of particles flowing in tubing, and measured speeds ranging from ∼0.35 mm/s to ∼1 mm/s. Note that only the magnitude of the flow could be determined, not its directionality in the lateral plane. The minimum and maximum measureable flow speeds were not investigated by the authors, but the maximum was likely determined by the optical focus size and the PRF: the particle must be in the focus during at least 3 laser pulses. The minimum was likely limited by the length of the total acquisition. The axial resolution was, as before, mainly determined by the transducer bandwidth, whereas the lateral resolution was determined simply by the optical focus.

Sarimallaoglu et al. applied the technique to estimate the flow speed of melanoma cells injected into mice [68]. They also used it in-vitro to determine whether gold nanorods (GNRs) were bound to breast cancer cells. They noticed a slower speed when GNRs were bound, arguing that unbound GNRs would flow in the centre of the tubing and these heavier cells would not. Besides investigating this transit time technique, Sarimallaoglu et al. also used a method similar to those in section 2.2.2, instead using three beams to record the time it takes melanoma cells to flow between these beams.

The method employed by both authors is limited to the detection of single particles or single cells: in an application on whole blood it is likely difficult to distinguish individual RBCs. Nevertheless, it might find an application in the detection of single contrast particles or circulating tumour cells in whole blood.

2.3.2. Transit-time flow imaging of particle ensembles

Yao & Wang and Chen et al. proposed a solution to make the single-particle method to more suitable for use on whole blood [69–72]. What holds for single particles also holds for a density distribution of particles moving through the focus. The faster the distribution moves through the optical focus, the sharper its features (the ‘peaks’) become (see Fig. 8). While it is ineffective to fit every single peak with a Gaussian function, it is relatively easy to compute either the autocorrelation or the bandwidth of the total photoacoustic acquisition: both determine the average peak width. For faster flow the autocorrelation coefficient becomes smaller, whereas the bandwidth increases, since the bandwidth is a Fourier transform pair with the autocorrelation function.

Fig. 8.

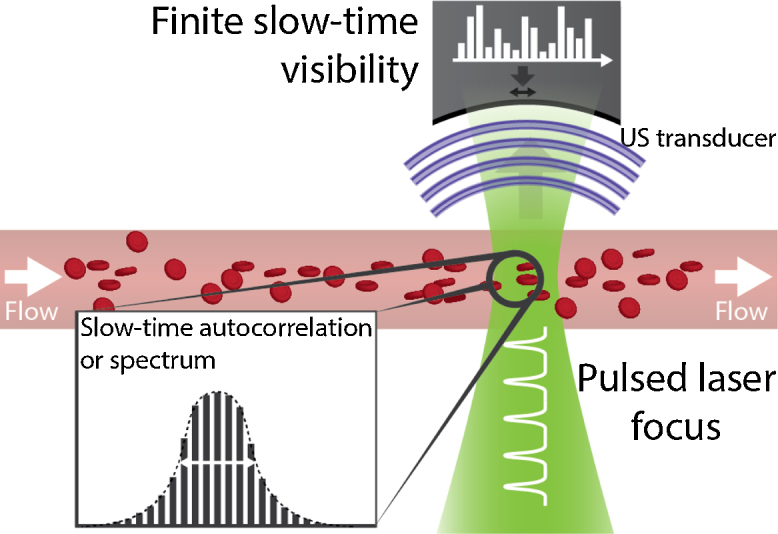
Transit-time principle for particle ensembles [69–72]. As cells transit the focus with a greater speed, features of the density distribution will show up with sharper peaks.

Starting with Yao and Wang, they used the slow-time bandwidth broadening for transverse flow velocity imaging [72]. As particles flow quicker through the focus, the transit time becomes shorter and the bandwidth, which is its inverse, broadens by:

$$B_d\approx f_0\frac{v_{trans}}{v_s}\frac{w}{R}\sin \left(\theta \right)$$

where $w$ is the optical focus width, $R$ the focal length and $f_0$ the centre frequency of the US transducer. The authors found their inspiration for this technique in OCT [73]. Yao and Wang applied the technique using an optical resolution PAM. They scanned the PAM back and forth, causing a change in broadening: an increase when moving against the flow and vice-versa. They used this change to determine the flow velocity via $v_{trans}=\sqrt{v_{t+}^2+v_{t-}^2-2v_m^2}$, where $v_{t+}$ and $v_{t-}$ are speeds measured in both directions while scanning, and $v_m$ is the motor speed. This scanning approach can be viewed as a combination of laser scanning confocal [36] and OCT [73].

They demonstrated the technique using particles (∅ 6 μm) flowing through tubing, with measureable flow velocities from ∼0.1 mm/s up to 2.5 mm/s. They also mapped the parabolic flow profile in the tubing. Yao et al., in a different article, subsequently applied the technique on blood-flow in-vitro and in-vivo [71]. In-vitro, they showed measureable flow velocities up to 5 mm/s, and used this to calibrate their in-vivo measurements. They finally applied their method to blood flow on vasculature in a chicken embryo (see Fig. 9), and were able to measure the flow-speed variations caused by the heart beating.

Fig. 9.

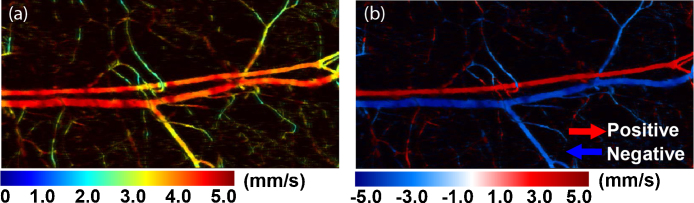
In-vivo example of flow mapping of the speed (a) and where the directionality is included (b). Adapted with permission from [71]. Copyright (2010) by OSA Publishing.

The theoretical maximum measureable flow velocity of this technique was limited by the optical focus and the PRF of the laser illumination, at about 7.4 mm/s. The minimum, indicated to be about 0.1 mm/s, was limited by SNR, and presumably acquisition time.

Chen et al. used the autocorrelation $G\left(\tau \right)=\delta P\left(t\right)\delta P\left(t+\tau \right)/P{\left(t\right)}^2$ to estimate the flow speed [69]. The autocorrelation function, when assuming a Gaussian optical focus, could be approximated by:

$$\frac{G\left(\tau \right)}{G\left(0\right)}=\exp \left(-{\left(\frac{\tau }{{\tau }_0}\right)}^2\right)$$

with ${\tau }_0=w/v_{trans}$. Instead of scanning the system, they limited themselves to estimating flow at a few locations, and therefore were not able to determine the flow direction. They demonstrated the method in their first article [69] using particles flowing at speeds from 14 μm/s to 200 μm/s. In their second article [70] they applied the method on chicken embryo vasculature, measuring flow speeds at individual locations 56-77 μm/s–based on an in-vitro calibration using particles.

Ning et al. used the autocorrelation approach to investigate blood flow in the ear of a nude mouse [74]. Using the diameter from the PA image, they were able to determine the volumetric flow rate of the vasculature, and the inflow and outflow at bifurcations. They calibrated their flow estimation and verified the computation of the volumetric flow rate both in-vitro.

Although not investigated by the authors of either approach, universal quantification of flow speed or velocity will remain difficult. The reason: quantification relies on knowledge of the optical focus and presumably also cell sizes. Although both can be either measured independently or otherwise calibrated for, the optical focus may increase through scattering, and RBCs can form clusters at small flow speeds.

Tay et al. proposed a technique to reduce the effect that optical scattering has on the optical focus [75]. They implemented wavefront shaping using the photoacoustic amplitude as a feedback mechanism. Wavefront shaping can be used to compensate for scattering by iteratively guessing the very complex phase-and-amplitude transformations that the input beam experiences. The ‘goodness’ of the guesswork was observed here using the photoacoustic amplitude, which therefore served as the feedback. This resulted in a bright optical spot at the location of the ultrasound focus. Tay et al. implemented the iterative process with a DMD projecting a series of Hadamard patterns on the sample. The optimal pattern could be found by multiplying the photoacoustic response of the m-th Hadamard pattern (vector $I_m$) by the inverse Hadamard matrix.

In this way, Tay et al. could measure the flow speed of particles behind a ground diffusor from ∼0.4 mm/s up to ∼2 mm/s. The random error of their measurements was–at ∼0.5 mm/s–quite high, which they attributed to particle size variations. The axial and lateral resolutions were governed here by the ultrasound transducer.

The optimization of the DMD pattern took 2 hours, making their setup unsuitable for tissue imaging as the authors note. To speed up the process, a faster DMD and laser would be required to beat the tissue dynamics, which are on a millisecond-timescale. A current limitation to their method is the inability to use wavefront shaping to focus on a spot inside and not behind a scattering medium. In theory the autocorrelation/bandwidth broadening technique likely also works based on just the acoustic focus, assuming the width and numerical aperture of the US transducer provide sufficient SNR without the optical focus.

2.4. Amplitude encoding

2.4.1. Photoconversion and replenishment

Li et al. estimated flow using a shape transition of gold nanorods [76]. Exciting the rods at their peak-absorption wavelength converts them to nanospheres, which have a different peak-absorption wavelength. Therefore, pulsing light on a volume of nanorods effectively photo-destroys the rods. After a light pulse, new nanorods will flow into the volume; a recovery that is related to the flow speed (see Fig. 10). Over time, repeated pulsing will bring the photoacoustic amplitude $P\left(k\right)$ down to a constant level $P_{const}$. The drop in amplitude could be approximated by:

$$P\left(k\right)=P_{const}+\left(1+P_{const}\right)r^k\exp \left(-u\frac{k}{PRF}\right)\text{,}$$

$$P_{const}=\frac{1-\exp \left(-u/PRF\right)}{1-r\exp \left(-u/PRF\right)}$$

with $k$ the k-th laser pulse, $u$ a parameter proportional to the flow speed, and $r$ a constant related to the laser power.

Fig. 10.

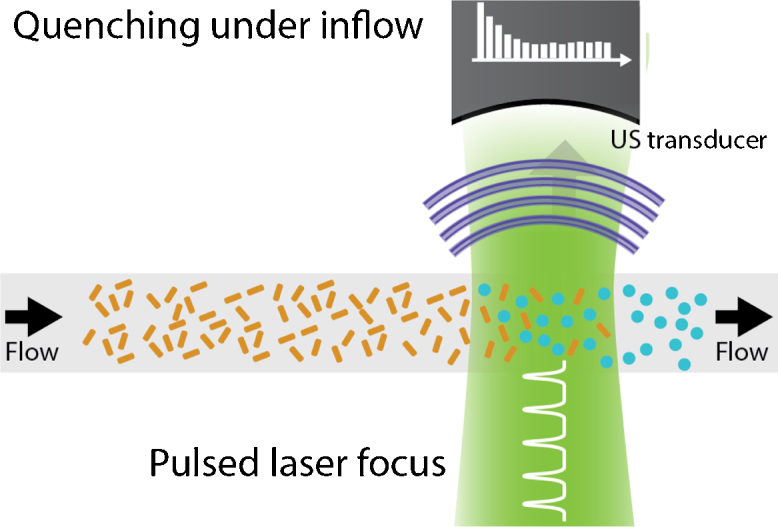
In the photoconversion and replenishment technique with constant energy [76], at every laser pulse, a fraction of the gold nanorods is converted into spheres. After every laser pulse, the rods replenish partly, until an equilibrium forms.

They estimated the flow speed of a suspension of gold nanorods flowing through tubing. They measured speeds from 0.35 mm/s up to 2.83 mm/s with a systematic error of ∼0.2 mm/s and random error of ∼30% the measured speed.

Wei et al. proposed an alternate method [77], using one initial high-energy laser pulse to convert a large fraction of the nanorods, and subsequently using lower-energy laser pulses to track the in-flow of new nanorods, as can also be seen in Fig. 11. The recovery of the photoacoustic amplitude could then be approximated by:

$$P\left(t\right)=1-c\exp \left(-\lambda v_{flow}t\right)\text{,}$$

with $c$ and $\lambda$ constants. This method is very similar to the ultrasound contrast flash-replenishment type methods, where a high-intensity burst of ultrasound is used to destruct micro-bubbles.

Fig. 11.

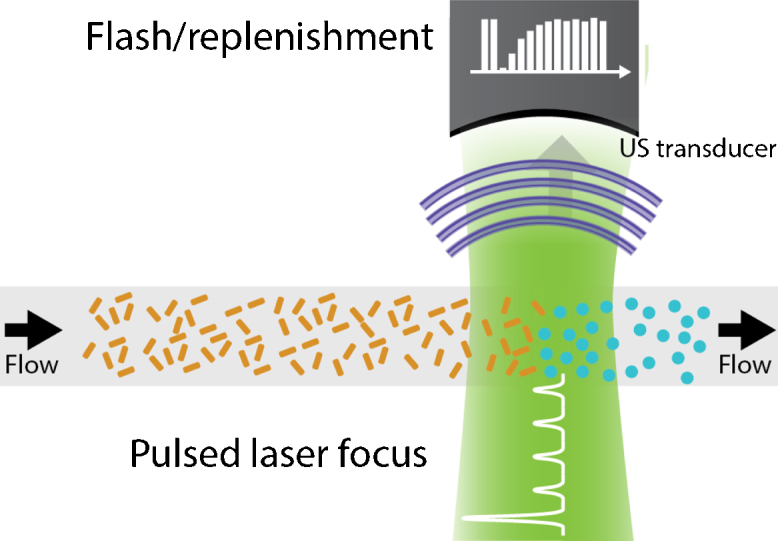
Flow measurement based on photoconversion using an a flash/replenishment approach [77]. A single intense laser pulse converts most of the nanorods, after which low intensity pulses are used to observe the rods’ replenishment.

The authors measured flow speeds of a GNR solution from 0.35 to 2.83 mm/s as before. They compared the photoacoustic flash-replenishment method with the constant-energy method from Li et al., but found the constant-energy method to provide the better performance. A reason for this might be, the authors write, their limited measurement time that made the measurements inaccurate.

Liao et al. implemented the constant-energy method with a linear array, providing B-mode flow imaging [78]. They also tested the performance under 5 mm of chicken breast, and could measure flow speeds from 0.125 to 2 mm/s with an average error of 30%. However, they had to recalibrate their measurements because the beam width had changed due to optical scattering. The axial and lateral resolutions were determined by the ROI selection in the B-mode image of the tubing, 0.6 mm and 1.2 mm respectively. The theoretical lower limits of these resolutions were determined by the point spread function of the system. The time resolution was determined by the total measurement time, 5-20 s depending on the settings.

Although not investigated by the authors, the maximum measureable speed–when there is only a relatively small drop in PA amplitude–was likely determined by the laser fluence at the GNRs and the measurement time. A larger fluence would cause a larger drop in amplitude and a longer measurement time would provide a more accurate determination of $P_{const}$. The minimum measureable speed likely depended on whether slow flow could be distinguished from no flow, which would be mainly determined by the SNR. Note that the authors did not mix the GNRs with blood, which might deteriorate the contrast further.

2.4.2. Heat encoding and convection

Sheinfeld and Eyal proposed the use of photothermal modulation for amplitude encoding [79]. They used two sine modulated laser diodes of different frequency to create an amplitude modulated photoacoustic signal: the heating of the medium increases its Grueneisen parameter and causes the photoacoustic response to increase (see Fig. 12). Modulating the heating process caused an amplitude modulation of the photoacoustic signal, of which the modulation frequency response was given by:

$$P\left({\omega }_{PT}\right)\propto \frac{t_{eff}}{1+j{\omega }_{PT}{t}_{eff}}$$

with ${\omega }_{PT}=2\pi f_{PT}$ the photothermal modulation frequency and $t_{eff}={\left(t_{conduction}^{-1}+t_{convection}^{-1}\right)}^{-1}$ a combination of time constants of conduction and flow-dependent convection. Sheinfeld and Eyal used a constant 0.5 MHz photoacoustic modulation and varied the PT modulation ${\omega }_{PT}$ from 0.1 Hz to 20 Hz. They fitted the observed $P\left({\omega }_{PT}\right)$ with the above function to determine $t_{eff}$. The authors obtained the contribution of conduction to $t_{eff}$ by measuring the response for zero flow, but found the contribution to be relatively small. They calibrated the relationship between $t_{eff}$ and the flow speed.

Fig. 12.

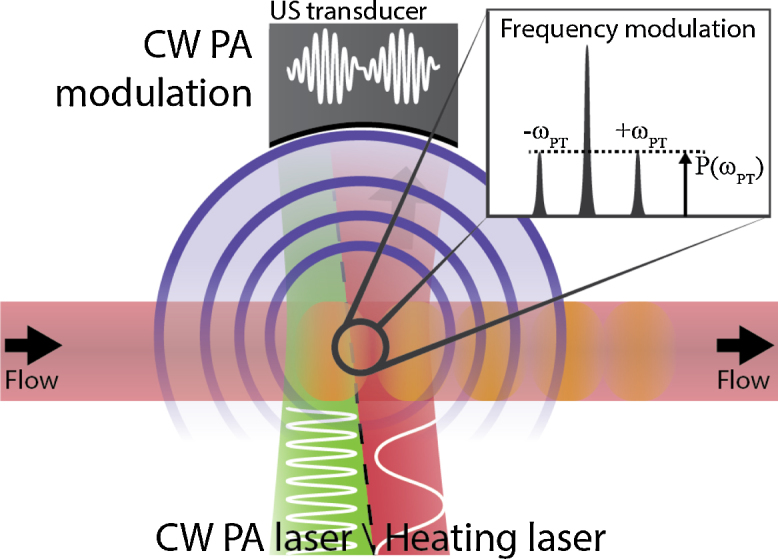
Flow measurement using photothermal modulation [79]. A low-frequency heating laser modulates the Gueneisen coefficient, which can be observed using a modulated PA laser.

The authors applied the PT modulation on sheep blood flowing through tubing, heating the blood less than 2 °C. They measured flows in a range of 1 to 21 mm/s. Their maximum error was 0.3 mm/s, which, when ignoring the contribution of conduction increased slightly to 0.75 mm/s. Although the authors did not investigate the speed limits, the minimum measureable speed was likely determined simply by whether flow and no flow can be distinguished, which might be dependent on whether the conduction can be modelled accurately. The maximum measureable speed was probably linked to the maximum modulation frequency, since for high flow speeds the modulation response changes only at higher frequencies. The axial resolution was likely very limited, whereas the lateral resolution was probably determined by the size of the heating beam. As with photoconversion, deep flow measurements with this technique are likely very challenging because optical scattering changes the size of the heating beam.

Wang et al. proposed to use ultrasound to heat the flowing medium [80] to solve the optical scattering issues with the above methods. They heated during a period of 300 ms, causing a 4 to 7 °C temperature increase, and measured the decrease in photoacoustic amplitude as the heated section travelled out of the ultrasound detection area. They found this decrease could be approximated by:

$$P\left(t\right)=c_1+c_2{e}^{-\lambda t}$$

with $c_1$ and $c_2$ constants and $\lambda =\lambda \left(v_{flow}\right)$ a flow-dependent decay constant. They implemented the method on an AR-PAM system to quantify bovine blood flowing through tubing under 1.5 mm chicken breast. After calibration they could measure flow speeds from 2.97 mm/s up to 41 mm/s.

Wang et al., in a separate paper, showed ultrasound-heating-based PA flowmetry using a tomography setup [81]. Instead of monitoring at a single point the photoacoustic response after heating, they used the tomography setup to reconstruct a 2D image of the tubing, in which they could track the movement of the heated spot (see Fig. 13). The setup was based on a HIFU transducer, which heated the medium with a 7.5 MHz waveform, which was modulated with a 0.0625 Hz sine to generate the heating in cycles. The amount heated was approximately 1 °C. The velocity could then be calculated from the rate at which the heating travels along the vessel at a certain radial position. This technique has some parallels with arterial spin labelling from MRI [15], although the spin labelling is used for perfusion imaging, and not for estimation of flow velocities because it allows longer labelling times but not a very rapid imaging rate.

Fig. 13.

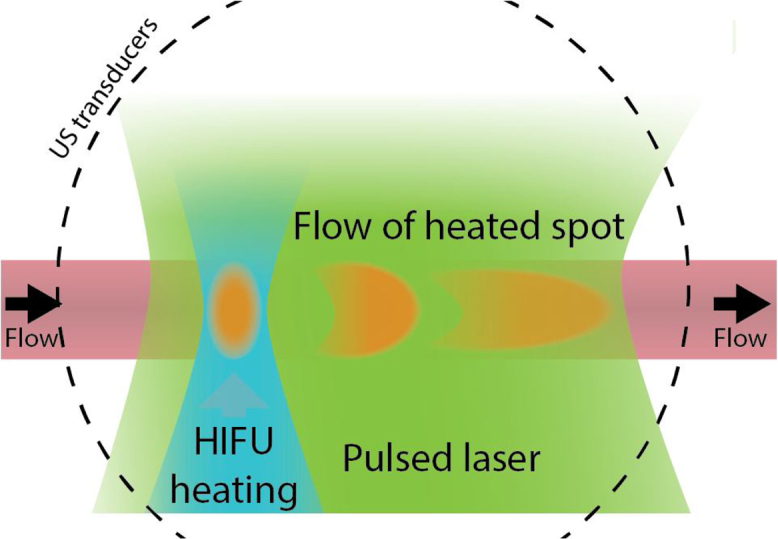
Flow measurement based on convection of an US-generated temperature increase [81]. High-frequency focussed ultrasound is emitted in bursts to heat a part of the flowing medium. The flow of this spot can be tracked using a photoacoustic tomography system.

Figure 14

Fig. 14.

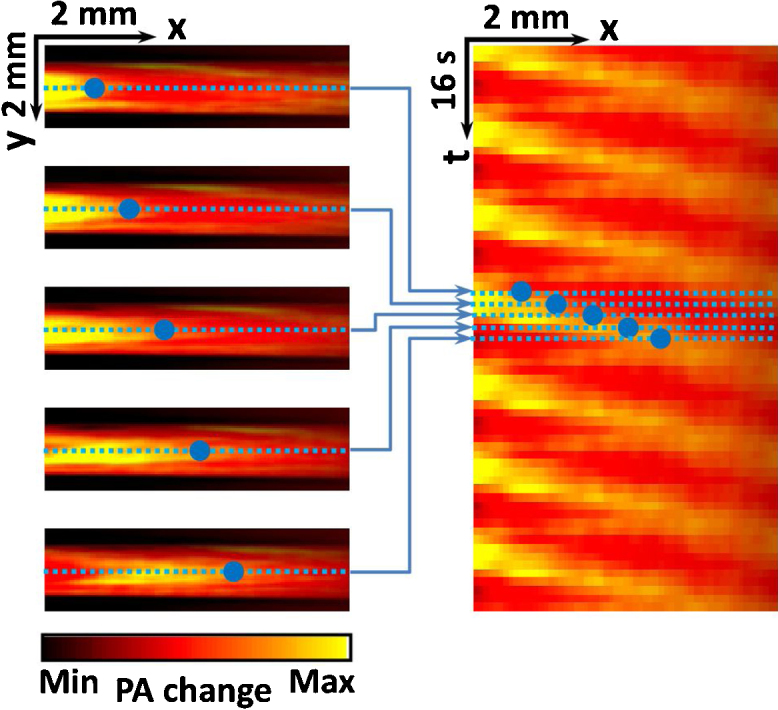
Example of in-vitro heat encoding. Adapted with permission from [81]. Copyright (2013) by The American Physical Society.

Wang et al. measured blood flow in tubing–without scattering–with velocities from 0.24 mm/s to 11.8 mm/s and a RMSE of 2.7%. They also showed a measurement under a 5 mm thick chicken breast layer with a single flow velocity, which they measured at 1.6 ± 0.2 mm/s. To achieve this they averaged over additional heating cycles (35 instead of 7).

Wang et al.’s minimum measureable velocity was determined by whether the flow was fast enough to ensure that the heated region was not yet smoothed by thermal conduction, and that the heated part would not be visible above the noise level. Their maximum measureable flow velocity was determined by the size of the field of view and the 2D imaging rate, since the heated spot needs to be within the field of view in at least a few images.

An advantage of this technique is its capability of imaging blood flow at diffuse optical depths, which is made possible due to the use of ultrasound instead of light for heating. Therefore, the maximum imaging depth will likely depend only on the SNR of the base photoacoustic response and on the acoustic attenuation by tissue of the HIFU cycles. The resolution in this case was likely optimal along the transducer axis and across the flow profile, however, along the flow direction it was limited by the distance the heated region was required to move.

Zhang et al. also applied this technique, but with optical CW heating instead of HIFU [82]. They implemented the technique on an OR-PAM system and scanned the microscope for 2D imaging instead of relying on a tomography system. Their analysis is identical to that of Wang et al. [81]. They could measure comparable in-vitro velocities (0.23 to 11 mm/s with a RMSE of 2%). Finally, they also successfully applied their technique to blood flow in a mouse ear.

2.5. Discussion and conclusion

In this review we investigated all the approaches that have been developed for photoacoustic blood flow imaging. Table 1 gives an overview of the key elements of each method. Our overview shows that photoacoustic flow imaging can overcome limitations of other modalities such as ultrasound and optical techniques. Photoacoustics allows a direct translation of flow imaging techniques from ultrasound pulse-echo, like the time-domain cross-correlation, or bandwidth broadening from OCT. There are also some similarities between heat encoding in PA and arterial spin labelling in MRI. But some approaches are unique for photoacoustics, like the spatial-domain Doppler flow imaging. All in all, a wide range of flow imaging methods is available, of which many warrant further investigation.

As described in the above review, not all methods are equally advanced in its development, and many have been applied only in-vitro with moderate results. Methods in the most advanced stage of development are the implementations using PA microscopy, having often been demonstrated in-vivo such as in a mouse ear or a chicken embryo. PAM allows high-frequency ultrasound detection and focussed optical excitation for an optimal SNR and interrogation of the densely packed red blood cells in blood–though at the cost of penetration depth.

Acoustic resolution setups also show promise, and a number of techniques, such as the tomography implemented heat encoding, have been shown to work under optical-scattering conditions. Signal tracking methods, such as the time-domain cross-correlation, in theory are also promising for tomography setups, as they are based only on the use of a pulsed laser. The methods do require some optimization of detection frequency and bandwidth however, for it seems that the same principle that makes PAI speckle-free at ∼5 MHz, will also smooth density variations in red blood cells. On the other hand, at higher frequencies it appears PAI might surpass ultrasound in the visibility of RBCs [47,48].

Up to now, PA flow imaging seems not yet applied clinically or pre-clinically. Although it will not likely compete with modalities like MRI or CT, it might find applications in areas where US, two-photon microscopy or OCT flow imaging are active. In the future, photoacoustic tomography and microscopy may provide flow imaging capabilities–exploiting its high contrast to haemoglobin–to applications ranging from rheumatoid arthritis diagnosis, to burn-wound assessment.

Conflict of interest

The authors declare that there are no conflicts of interest.

Biographies

Pim van den Berg is a PhD researcher at the University of Twente, the Netherlands. He is working on the European project Fullphase, which aims to develop an affordable and portable ultrasound/photoacoustic (US/PA) system for early disease detection. His main research interests are flow imaging using photoacoustics and the application of US/PA imaging for the assessment of rheumatoid arthritis. Before starting his PhD, Pim did his master studies on Optics and Biophysics, building a STORM super resolution microscope and used it for characterization of protein aggregation in Parkinson's disease. Interests also include high school science promotion, having participated in a media push around photoacoustic imaging for the popularization of applied sciences.

Khalid Daoudi received his PhD degree in Applied Optics from university Pierre et Marie Curie, Paris, France for his work on transient opto-elastography. He is currently working as Postdoctoral researcher at the Institute for Biomedical Technology and Technical Medicine, BMPI group, university of Twente in Netherlands. His research focuses on optical and hybrid acoustical and optical imaging methods: photoacoustics, acousto-optics, light tissue interaction and ultrasound.

Wiendelt Steenbergen obtained a master degree in aerospace engineering at the University of Technology in Delft. In 1995 he obtained a PhD degree in fluid dynamics at the Eindhoven University of Technology. In 1995 he joined the University of Twente, Enschede (the Netherlands) as a postdoc. In 2000 he was appointed assistant professor in biomedical optics in 2000 and broadened his scope to low coherence interferometry and photoacoustic and acousto- optic imaging. In 2007-2008 he was visiting researcher in the Kroto Institute of the University of Sheffield. In 2008 he was appointed associate professor, and in 2010 he became full professor and group leader of the newly formed Biomedical Photonic Imaging group of the University of Twente.