Accelerated Whole-Brain Multi-Parameter Mapping using Blind Compressed Sensing

Abstract

Purpose

To introduce a blind compressed sensing (BCS) framework to accelerate multi-parameter MR mapping, and demonstrate its feasibility in high-resolution, whole-brain T_1ρ and T₂ mapping.

Methods

BCS models the evolution of magnetization at every pixel as a sparse linear combination of bases in a dictionary. Unlike compressed sensing (CS), the dictionary and the sparse coefficients are jointly estimated from under-sampled data. Large number of non-orthogonal bases in BCS accounts for more complex signals than low rank representations. The low degree of freedom of BCS, attributed to sparse coefficients, translates to fewer artifacts at high acceleration factors(R).

Results

From 2D retrospective under-sampling experiments, the mean square errors in T_1ρ and T₂ maps were observed to be within 0.1% up to R=10. BCS was observed to be more robust to patient-specific motion as compared to other CS schemes and resulted in minimal degradation of parameter maps in the presence of motion. Our results suggested that BCS can provide an acceleration factor of 8 in prospective 3D imaging with reasonable reconstructions.

Conclusion

BCS considerably reduces scan time for multi-parameter mapping of the whole brain with minimal artifacts, and is more robust to motion-induced signal changes compared to current CS and PCA based techniques.

INTRODUCTION

The quantification of multiple tissue parameters from MRI datasets is emerging as a powerful tool for tissue characterization (1-8). Parameters such as proton density, longitudinal and transverse relaxation times (denoted by T₁ and T₂), relaxation times in the rotating frame (T_1ρ and T_2ρ), as well as diffusion have been shown to be useful in diagnosis of various diseases including cerebral ischemia (9), Parkinson’s disease (2-4), Alzheimer’s disease (2, 5, 7), epilepsy (7) multiple sclerosis (6, 7), edema (8), necrosis (8), liver fibrosis (10), and intervertebral disc and cartilage degeneration (11-13). Although a single parameter may be sensitive to a number of tissue properties of interest, it may not be specific. Acquiring additional parameters can improve the specificity. The main bottleneck in the routine clinical use of multi-parameter mapping is the long scan time associated with the acquisition of MR images with multiple weightings or contrast values. In addition, long scan times are likely to result in motion induced artifacts in the data.

A common approach to reduce the scan time is to limit the number of weighted images from which the parameters are estimated. However, this approach precludes the use of multi-exponential fitting methods, limits the accuracy of fits, and restrict the dynamic range of estimated tissue parameters. Several researchers have proposed to accelerate the acquisition of the weighted images using parallel imaging, model-based compressed sensing, and low-rank signal modeling (14-22). The use of parallel imaging alone can only provide moderate acceleration factors (14). Model-based compressed sensing methods rely on large dictionaries generated by Bloch equation simulations of all possible parameter combinations (23). A challenge associated with this scheme is its vulnerability to patient motion, mainly because the dictionary basis functions cannot account for motion induced signal changes. Another problem with the direct application of this scheme to multi-parameter imaging is the rapid growth in the size of the dictionaries with the number of parameters, which also results in increased complexity of the non-linear recovery algorithm. In this context, methods such as k-t PCA and PSF models that estimate the basis functions from the measured data itself are more desirable; the basis functions can model motion induced signal changes and thus provide improved recovery of weighted images (22, 24).

The main contribution of this paper is to optimize the blind compressed sensing (BCS) scheme, which was originally introduced for dynamic imaging (25), to accelerate multi-parameter mapping. The BCS scheme represents the evolution of the magnetization of the pixels as a sparse linear combination of basis functions in a finite dictionary V. Specifically, the Casorati matrix of the data X is modeled as X = UV. This model is ideally suited for multi-parameter mapping since there are finite number of distinct tissue types in the specimen with unique parameter values. The proposed algorithm learns the dictionary basis functions, as well as their sparse coefficients U, from the undersampled data by solving a constrained optimization problem. The criterion is a linear combination of the data fidelity term and a sparsity promoting ℓ₁ norm on the coefficient matrix U, subject to the Frobenius norm constraint on the dictionary V. Unlike methods such as (26) that pre-estimate the dictionary, this approach provides robustness to patient-specific motion. When the data is truly low-rank, the k-t PCA and PSF schemes (22, 24) requires very few basis functions to represent it. However, in many cases (e.g. in the presence of motion, multiple tissue types, and simultaneous mapping of multiple parameters), the rank of the dataset can be considerably higher; the larger degrees of freedom will translate to a tradeoff between accuracy and artifacts, especially at high acceleration factors. The BCS scheme uses a considerably larger dictionary of non-orthogonal basis functions, which provides a richer representation of the data compared to the smaller dictionary of orthogonal basis functions used in the k-t PCA and PSF schemes. The sparsity of the coefficients ensures that the number of active basis functions at each voxel are considerably lower than the rank of the dataset. Since the basis functions used at different spatial locations are different, the BCS scheme can be viewed as a locally low-rank scheme; the appropriate basis functions (subspace) at each voxel are selected independently. Since the number of basis functions required at each voxel is considerably lower than the global rank, the BCS scheme can provide a richer representation with lower degrees of freedom; this translates to better trade-offs between accuracy and achievable acceleration, especially in multi-parametric datasets with inter-frame motion.

The BCS algorithm (25) was inspired by the theoretical work on BCS by Gleichman et al. (27). The work by Gleichman et. al. considers the same sensing matrix for all time frames, for simplicity of the derivations. The proposed scheme uses different sensing matrices for different frames. The experiments in (25, 28) clearly demonstrate the benefit of higher spatial and temporal incoherency offered by this sampling strategy. In addition, the algorithm used in (27) is fundamentally different from our setting. The proposed scheme is also motivated by and have similarities to the partial separable function (PSF) model introduced by Liang et al. (16, 24, 29). However, there are several key differences between the PSF implementations and the proposed scheme. For example, (24) uses the power factorization method to exploit the low-rank structure of X. They jointly estimate U and V by alternating between two quadratic optimization schemes involving data consistency terms. Our previous work shows that the BCS scheme provides improved re-constructions than low-rank methods, including power-factorization (24, 25), mainly because of the richer dictionary and the lower degrees of freedom. Zhao et. al, assumes the data to be low-rank and pre-estimates the orthogonal basis set V from low resolution data (29); they then estimate the coefficients using a sparsity penalty on U. This approach can be seen as the first step of our iterative algorithm to jointly estimate U and V. Specifically, the joint estimation of U and V will provide a richer dictionary with non-orthogonal basis functions, which provide sparser coefficients than the orthogonal basis functions in (29). This is not unexpected since extensive work in image processing have shown that over-complete and non-orthogonal dictionaries/frames offer more compact representations than orthogonal basis sets. The comparisons in Fig. 4 demonstrate the performance improvement offered by the proposed joint estimation scheme.

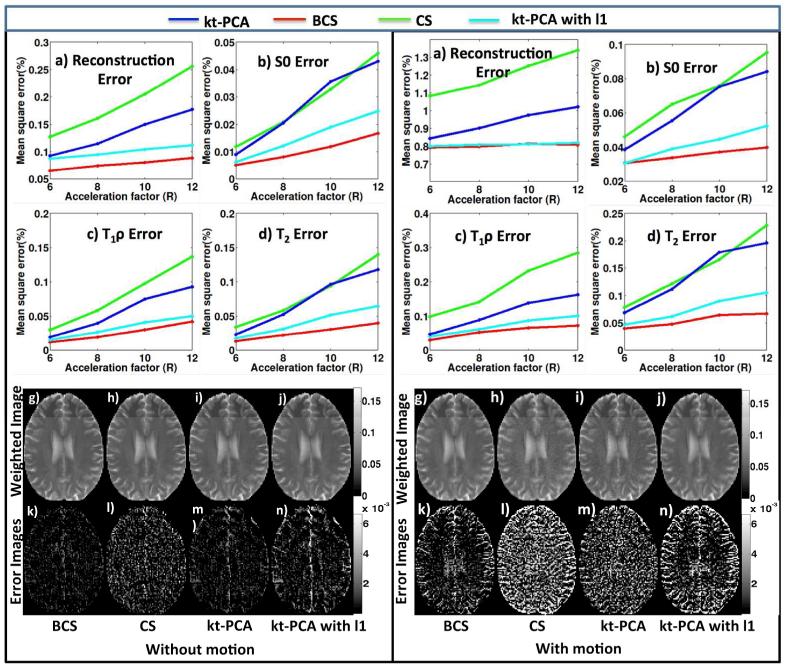
Fig. 4.

Comparison of the proposed BCS scheme with different reconstruction schemes on retrospectively under-sampled 2D dataset: The results for dataset without and with motion are shown in (i) and (ii) respectively. The plots for reconstruction error, S₀ map error, T_1ρ map error and T₂ map error for BCS, CS, kt-PCA and kt-CPA with ℓ₁ sparsity schemes are shown in (a-d). It is observed that the BCS scheme provides better recovery in both cases. The images in (g-j) show one weighted image of the reconstructed dataset at acceleration factor of 8 using the 4 different schemes. We observe that the CS and kt-PCA schemes were sensitive to motion and resulted in spatial blurring as seen in (ii)- (h-j), which is also evident from the error images.

We study the utility of the proposed BCS scheme to simultaneously recover T_1ρ and T₂ maps from under-sampled weighted images. We rely on Cartesian sub-sampling schemes. The proposed scheme yields reasonable estimates from the whole-brain for eight fold under-sampling over the fully-sampled setup, thereby reducing the scan time to 20 min.

METHODS

In a multi-parameter imaging, the k-space data corresponding to different image contrasts are often sequentially acquired by manipulating the sequence parameters (e.g. echo time, spin lock duration/amplitude and flip angle). We denote the parametric dimension by p. The multi-coil under-sampled acquisition of such an experiment is modeled as:

$$\mathbf{b}(\mathbf{k},p)=\mathcal{A}\left[\gamma \right(\mathbf{x},p\left)\right]+\mathbf{n}(\mathbf{k},p),$$ [1]

where b(k, t) represents the concatenated vector of the k – p measurements from all the coils. γ(x, p)(x = (x₁, y₁)) denotes the underlying images pertaining to different contrasts; and n is additive noise. $\mathcal{A}$ is the operator that models coil sensitivity and Fourier encoding on a specified k – p sampling trajectory.

Blind compressed sensing (BCS) formulation

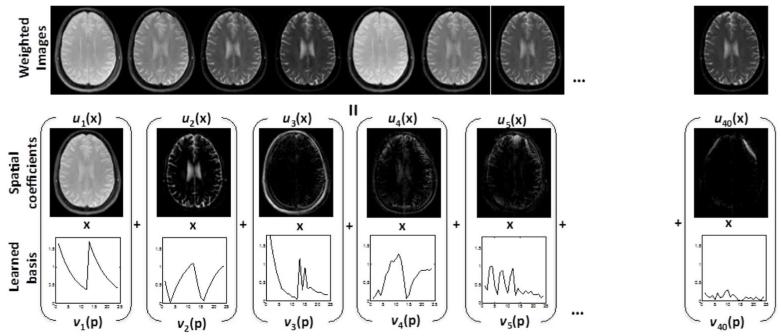
The BCS model relies on the assumption that there exists a finite number of distinct tissue types with unique relaxation parameter values within the specimen of interest; the evolution of the magnetization of the tissue types as a function of p can be represented efficiently as a linear combination of basis functions in a dictionary V_R×N. Here R denotes the total number of basis functions in the dictionary and N is the total number of contrast weighted images in the dataset. The signal evolution at the pixel specified by x is modeled as a sparse linear combination of basis functions v_i(p); i = 1, ..R in V (Also see Fig 1.):

$$\gamma (\mathbf{x},p)=\sum _{i=1}^R\underset{\text{sparse}\text{spatial}\text{weights}}{\overset{u_i\left(\mathbf{x}\right)}{\underbrace{}}}\underset{\text{learned}\text{bases}}{\overset{v_i\left(p\right)}{\underbrace{}}}.$$ [2]

Using the Casorati matrix notation (16), the above equation can be rewritten as

$${\Gamma }_{M\times N}=\left(\begin{array}{ccc}\hfill \gamma ({\mathbf{x}}_1,p_1)\hfill & \hfill .\hfill & \hfill \gamma ({\mathbf{x}}_1,p_N)\hfill \\ \hfill .\hfill & \hfill .\hfill & \hfill .\hfill \\ \hfill .\hfill & \hfill .\hfill & \hfill .\hfill \\ \hfill \gamma ({\mathbf{x}}_M,p_1)\hfill & \hfill .\hfill & \hfill \gamma ({\mathbf{x}}_M,p_N)\hfill \end{array}\right)={\mathbf{U}}_{M\times R}{\mathbf{V}}_{R\times N},$$ [3]

where M is the total number of pixels in the image, u_i(x) and v_i(p) in Eq. [2] are respectively the i^th column and row entries of U, V. We formulate the joint recovery of U, V from under-sampled multi-coil k – p measurements as the following constrained minimization problem:

$$\{{\mathbf{U}}^{\ast },{\mathbf{V}}^{\ast }\}=\underset{\mathbf{U},\mathbf{V}}{\arg \min }\underset{\mathcal{C}(\mathbf{U},\mathbf{V})}{\overset{{\mid \mid \mathcal{A}\left(\mathbf{UV}\right)-\mathbf{b}\mid \mid }_F^2+\lambda {\mid \mid \mathbf{U}\mid \mid }_{l_1}}{\underbrace{}}}\text{such}\text{that}{\mid \mid \mathbf{V}\mid \mid }_F^2<1.$$ [4]

The first term in Eq. [4] ensures data consistency. The second term promotes sparsity on the spatial coefficients u_i(x) by utilizing a convex ℓ₁ norm prior on U, which is given by ${\mid \mid \mathbf{U}\mid \mid }_{l_1}=\left({\Sigma }_{i=1}^M{\Sigma }_{j=1}^r\mid u(i,j)\mid \right)$, and λ is the regularization parameter. The optimization problem is constrained by imposing unit Frobenius norm on the over-complete dictionary V, making the recovery problem well posed. Note that we are jointly estimating the sparse coefficients U and the subject-specific dictionary V directly from the under-sampled k – p data. Since the dictionary is subject-specific, this approach ensures that any deviations from the true parametric encoding, such as subject motion, field inhomogeneity and chemical shift artifacts, are learned by the basis functions. The number of active bases at a specified voxel depends on several factors that include partial volume effects, motion, and magnetization disturbances due to inhomogeneity artifacts. The spatial weights u_i(x) are encouraged to be sparse since we expect only a few tissue types to be active at any specified voxel. The main difference of the proposed implementation from (25) is the use of an efficient algorithm and the extension to multi-coil formulation which enables better recovery at high acceleration rates.

Fig. 1.

BCS model representation: The model representation of the multi-parameter signal of a single brain slice with 24 parametric measurements (12 TEs and 12 TSLs) is shown above. The signal Γ is decomposed as a linear combination of Spatial weights u_i(x) (x are the spatial locations (pixels)) and temporal basis functions in v_i(p) (p are the parametric measurements). We observe that only 3-4 coefficients per pixel are sufficient to represent the data. The Frobenius norm attenuates the insignificant basis functions.

Optimization Algorithm

We majorize an approximation of the ℓ₁ penalty on U in (4) as ${\mid \mid \mathbf{U}\mid \mid }_{{\ell }_1}\approx {\min }_{\mathbf{L}}\frac{\beta }{2}{\mid \mid \mathbf{U}-\mathbf{L}\mid \mid }^2+{\mid \mid \mathbf{L}\mid \mid }_{{\ell }_1}$, where L is an auxiliary variable. This approximation becomes exact as β → ∞. When β is small, the majorization is equivalent to the Frobenius norm on U (30). We use a variable splitting and augmented Lagrangian optimization scheme to enforce the constraint in Eq. [4]. Thus, the optimization problem corresponds to

$$\{{\mathbf{U}}^{\ast },{\mathbf{V}}^{\ast }\}=\arg \underset{\mathbf{U},\mathbf{V}\mathbf{Q},\mathbf{L}}{\min \min }{\mid \mid \mathcal{A}\left(\mathbf{UV}\right)-\mathbf{b}\mid \mid }_F^2+\frac{\beta }{2}{\mid \mid \mathbf{U}-\mathbf{L}\mid \mid }^2+\lambda {\mid \mid \mathbf{L}\mid \mid }_{l_1}\text{such}\text{that}{\mid \mid \mathbf{Q}\mid \mid }_F^2<1,\mathbf{V}=\mathbf{Q}$$ [5]

Here, Q is the auxiliary variable for V. The constraint V = Q is enforced by adding the augmented Lagrangian term $\frac{\alpha }{2}{\mid \mid \mathbf{V}-\mathbf{Q}\mid \mid }^2+\langle \Lambda ,(\mathbf{V}-\mathbf{Q})\rangle$ to the above cost function. Here, Λ is the Lagrange multiplier term that will enforce the constraint. These simplifications enable us to decouple the optimization problem in (4) into different sub-problems. We use an alternating strategy to solve for the variables U, V, Q and L. All of these sub-problems are solved independently in an efficient fashion as described below, assuming the other variables to be fixed.

Update on L: The sub-problem can be solved analytically as

$${\mathbf{L}}_{n+1}=\frac{\mathbf{U}}{\mid {\mathbf{U}}_n\mid }{\left(\mid {\mathbf{U}}_n\mid -\frac{1}{\beta }\right)}_{+}$$ [6]

where ‘+’ represents the soft thresholding operator defined as (τ)₊ = max{0, τ} and β is the penalty parameter.

Update on U: The sub-problem on U, assuming the other variables to be fixed, can be written as

$${\mathbf{U}}_{n+1}=\underset{\mathbf{U}}{\arg \min }{\mid \mid \mathcal{A}\left({\mathbf{U}}_n{\mathbf{V}}_n\right)-\mathbf{b}\mid \mid }_2^2+\frac{\lambda \beta }{2}{\mid \mid \mathbf{U}-{\mathbf{L}}_{n+1}\mid \mid }_2^2$$ [7]

Since it is a quadratic problem, we solve it using a conjugate gradient (CG) algorithm. Here, U_n, V_n and L_n are the variables at the n^th iteration.

Update on Q: This sub-problem, assuming the other variables to be fixed, is solved using a projection scheme as specified in Eq. [8].

$${\mathbf{Q}}_{n+1}=\{\begin{array}{cc}{\mathbf{V}}_n\hfill & \text{when}{\mid \mid {\mathbf{V}}_n\mid \mid }_F^2\le 1\hfill \\ \frac{1}{{\mid \mid {\mathbf{V}}_n\mid \mid }_F}{\mathbf{V}}_n\hfill & \text{else}\hfill \end{array}\phantom{\}}$$ [8]

Note that Q_n is obtained by scaling V_n so that the Frobenius norm is unity.

Update on V: Minimizing the cost function with respect to V, assuming other variables to be constant yields

$${\mathbf{V}}_{n+1}={\mid \mid \mathcal{A}\left({\mathbf{U}}_{n+1}{\mathbf{V}}_n\right)-\mathbf{b}\mid \mid }_F^2+<{\Lambda }_n,{\mathbf{V}}_n-{\mathbf{Q}}_{n+1}>+\frac{\alpha }{2}{\mid \mid {\mathbf{V}}_n-{\mathbf{Q}}_{n+1}\mid \mid }_F^2.$$ [9]

The quadratic problem is solved using a CG algorithm. This usually takes a few steps to converge. We use the steepest ascent method to update the Lagrange multiplier at each iteration

$${\Lambda }_{n+1}={\Lambda }_n+\alpha ({\mathbf{V}}_{n+1}-{\mathbf{Q}}_{n+1})$$ [10]

The convergence of the algorithm depends on α and β parameters. Since we use the augmented Lagrangian framework for enforcing constraint on the dictionary, it is not necessary for α to tend to ∞ for the constraint to hold, allowing faster convergence. However, α is progressively updated every iteration to improve the convergence. The inner loop is terminated once the constraint is satisfied, meaning the difference between V and Q is less than a threshold of 10⁻⁵. In contrast, for the majorization to well approximate the ℓ_p penalty, β needs to be a high value. As discussed earlier, the majorization is only exact when β → ∞. Since the condition number of the U sub-problem is dependent on β, convergence of the algorithm will be slow at high values of β. In addition, the algorithm may converge to a local minimum if it is directly initialized with a large β value. Hence, we use a continuation on β, where we initialize it with a small value and increment it gradually when the cost in Eq. [4] stagnates to a threshold level of 10⁻³. Our previous work shows that this strategy significantly minimizes the convergence of the algorithm to local minima (25). The outer loop is terminated when constraints for sparse approximation are achieved; in other words, when the cost function given in Eq. [4] converges to a threshold value of 10⁻⁶.

The pseudo-code of the algorithm is shown below.

Algorithm.

BCS(A, b, λ)

Data Acquisition

To demonstrate the utility of the proposed BCS scheme in recovering T_1ρ, T₂ and S₀ parameters, healthy volunteers were scanned on a Siemens 3T Trio scanner (Siemens Healthcare, Erlangen, Germany) using a vendor provided 12-channel phased array coil. Written informed consent was obtained and the study was approved by the Institutional Review Board. The coil sensitivity maps were obtained using the Walsh method for coil map estimation (31).

To test the feasibility of the algorithm and to optimize the parameters, we first acquired a single-slice fully-sampled axial 2D dataset using a turbo spin echo (TSE) sequence, combined with T_1ρ preparatory pulses (32) and T₂ preparatory pulses (33). Scan parameters were turbo factor (TF) of 8, matrix size = 128×128, FOV= 22×22cm², TR=2500ms, slice thickness =5mm, B₁ spin lock frequency=330Hz, and band-width= 130Hz/pixel. T_1ρ and T₂ weighted images were obtained by changing the duration of the T_1ρ (referred as spin lock time) and duration of the T₂ preparation pulses (referred as echo time) respectively. The data was collected for 12 equi-spaced spin lock times (TSLs) and 12 equi-spaced echo times (TEs) values, both ranging from 10 ms to 120 ms. This provided a total of 24 parametric measurements. The scan time for this dataset was 16 min. Note that five or six spin lock times are sufficient for T_1ρ estimation using a single exponential fit. However, our main motivation is the future use of this scheme for multi-parametric mapping (e.g. joint imaging of T_1ρ, T₂, T_1ρ dispersion imaging, as well as time-resolved parametric mapping). The proposed scheme will prove very useful in these settings. Moreover, larger number of parametric images are essential for more sophisticated models such as multi-exponential model to account for partial volume issues.

To demonstrate the utility of the approach in accelerated 3-D imaging, we acquired a prospective 3D dataset using a segmented 3D gradient echo sequence based on the 3D MAPSS approach (34). Scan parameters were FOV = 22×22×22cm³, matrix size = 128×128×128, 64 lines/segments, TR/TE=5.6/2.53ms, recovery time=1500ms, resolution 1.7mm isotropic, bandwidth= 260Hz/pixel, B₁ spin lock frequency =330Hz and constant flip angle=10°. The readout (frequency encode) direction was (k_x), which enabled us to choose an arbitrary sampling pattern. TEs and TSLs of the T₂ and T_1ρ preparation pulses were varied uniformly from 10 to 100ms providing 10 measurements of each. Scan time of the prospective 3D dataset was 20 min. To be consistent with the 2D dataset the phase encoding plane (phase encode, slice encode) was oriented along the axial (k_y – k_z) plane. We perform the recovery of each y – z slice independently.

Optimization & validation of the algorithm using fully sampled 2-D acquisition

We used the fully sampled 2-D dataset to determine an optimal sampling pattern, optimize the parameters, and compare with other algorithms.

Determination of a sampling scheme

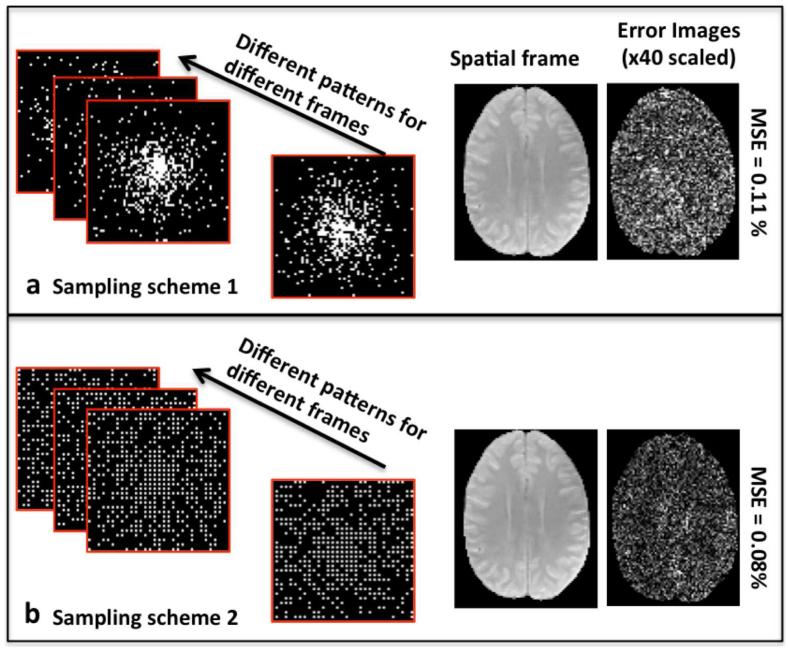
To choose an optimal sampling scheme that will work well with the multi-channel BCS scheme, we retrospectively under-sample the 2-D dataset using two different under-sampling schemes shown in Fig 2.(a-b). Both patterns correspond to an 8 fold under-sampling. Fig. 2(a) shows the pseudo-random variable density trajectory which over-samples the center of k-space. The sampling scheme 2 as shown in Fig. 2(b) is a combination of a 2×2 uniform Cartesian under-sampling pattern and a pseudo-random variable density pattern as in Fig. 2(a). Acceleration factor of 6,8,10 and 12 were achieved as 4- fold uniform under-sampling and 1.5, 2, 2.5 and 3 fold random variable density under-sampling respectively. The 2×2 uniform sampling pattern for different frames is randomly integer shifted in the range [x, y] = [−1, 1]×[−1, 1] as done in (35) to achieve more incoherency. This sampling scheme may be replaced with Poisson disc sampling (36). We compare the reconstructions provided by the proposed algorithm from the dataset under-sampled using both schemes.

Fig. 2.

Choice of sampling trajectories: The sampling patterns for a specific frame for the two choices of sampling schemes are shown in (a) and (b), respectively. The results are shown for an under-sampling factor of 8. The first sampling scheme (shown in (a)) is a pseudo-random variable density pattern, while the second sampling scheme (shown in (b)) is a combination of a uniform 2×2 under-sampling pattern and a pseudo-random variable density pattern. The second column shows one of the weighted images of the reconstructed data using BCS. As seen from the error images in third column, sampling scheme 2 yields better performance. Note that the sampling patterns are randomized over different parameter values to increase incoherency.

Details of algorithms & determination of their parameters

We compare the BCS algorithm against compressed sensing (CS) (26) and k-t principal component analysis (PCA) (22) methods. A training dataset of 10000 exponentials is generated assuming the exponential model in Eq. [12] for the CS scheme. A dictionary of 1000 atoms is learned from the training dataset using k-SVD algorithm (37). Specifically, we vary the T₂ and T_1ρ values from 1ms to 300ms in steps of 3. The learned dictionary is then optimized for signal approximation with at most K atoms. The sparsity value K is chosen as 7 based on the model fit with respect to fully sampled dataset. The dictionary learned from the training phase is used in the reconstruction. The data is reconstructed using an iterative procedure, which iterates between obtaining the K-term estimate of the signal using orthogonal matching pursuit (OMP) algorithm and minimizing data consistency as described in (26). kt-PCA is implemented as a two step approach where the first step is to estimate the orthogonal basis functions from the training data. The basis functions are estimated from the center 9×9 grid of the fully-sampled k-space data using PCA. In the second step, the estimated basis functions are used in reconstruction of the data. We also compare the BCS algorithm with the kt-PCA method with ℓ₁ sparsity constraint enforced on the coefficients. The algorithms are implemented in MATLAB on a quad core linux machine with a NVDIA Tesla graphical processing unit. The regularization parameters of all the algorithms were chosen such that the error between reconstructions and the fully-sampled data specified by

$$\mathrm{MSE}=\left(\frac{{\mid \mid {\Gamma }_{\mathrm{recon}}-{\Gamma }_{\mathrm{orig}}\mid \mid }_F^2}{{\mid \mid {\Gamma }_{\mathrm{orig}}\mid \mid }_F^2}\right)$$ [11]

is minimized. We iterate all algorithms until convergence (until the change in the criterion/cost function is less than a threshold which is 10e-6). With this setting, kt-PCA takes about 10-15 iterations, kt-PCA with ℓ₁ constraint takes 7-8 iterations, BCS takes 60-70 iterations while CS takes around 100 iterations to converge.

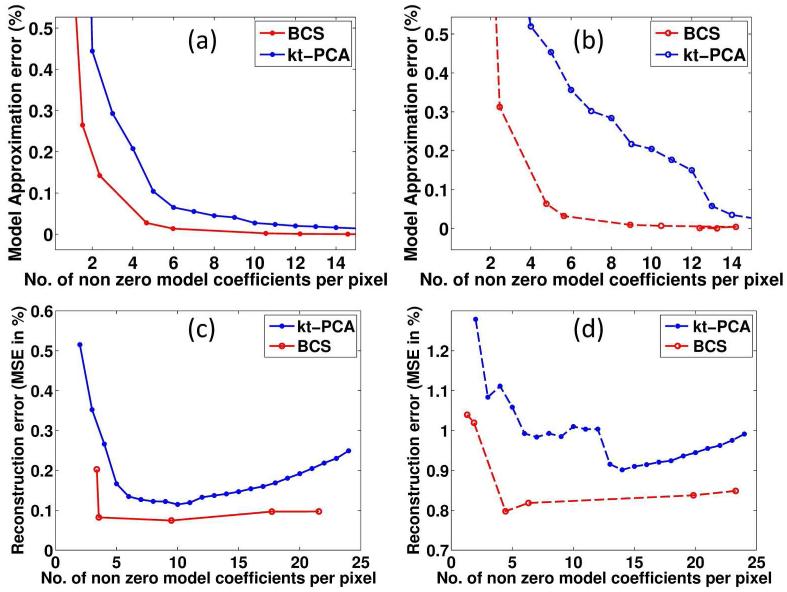
We also compare the BCS and kt-PCA methods for their compression capabilities. The 2D dataset with and without motion is represented using different number of basis functions in case of kt-PCA and different regularization parameters (and equivalently different sparsities) in case of BCS. For BCS model we considered dictionary V_us estimated from 6 fold under-sampled data. To determine the model representation at different compression factors we solved for the model coefficients U using the following equation:

$${\widehat{\mathbf{U}}}_{\lambda }=\arg \underset{\mathbf{U}}{\min }{\mid \mid \Gamma -{\mathbf{UV}}_{us}\mid \mid }_2^2+\lambda \mid \mid \mathbf{U}\mid \mid {\ell }_1$$ [12]

We varied the range of λ and minimized the above problem to control the sparsity levels of ${\widehat{\mathbf{U}}}_{\lambda }$, and hence the compression capabilities. A threshold of 0.1 % was applied on ${\widehat{\mathbf{U}}}_{\lambda }$ to shrink the coefficients that were very small and were not fully decayed to zero during the above ℓ₁ minimization problem. The model approximation error is given by ${\mid \mid \Gamma -{\mathbf{U}}_{\lambda }{\mathbf{V}}_{\mathbf{us}}\mid \mid }_F^2$.

Comparison of the algorithms

We estimate the parameters S₀, T_1ρ and T₂ by fitting the mono-exponential model

$$M\left(p\right)=S_0.\exp \left(\frac{-\mathrm{TE}\left(c\right)}{T_2}\right).\exp \left(\frac{-\mathrm{TSL}\left(c\right)}{T_{1\rho }}\right)$$ [13]

to the reconstructed images on a pixel by pixel basis using a linear least-squares algorithm. The mean square error (MSE) of the parameter maps obtained from the BCS, CS and kt-PCA algorithms are compared to the ones obtained from the fully-sampled data. We mask the reconstructed images before computing the parameter maps to limit our evaluation of T_1ρ, T₂ and S₀ to the brain tissue.

The performance of the reconstruction scheme at higher acceleration was assessed by retrospectively under-sampling the dataset at acceleration factors of 6, 8, 10, 12 & 15 using the sampling scheme shown in Fig. 2(b). To determine the robustness of the proposed scheme to motion, we constructed a simulated dataset with inter-frame motion by adding translational motion resulting in 1 pixel shift and rotational motion of 1 degree to frames 16-21 of the 2D dataset, out of 24 frames. The reconstructed images are aligned to compensate for inter frame motion, prior to fitting. To demonstrate the advantage of acquiring multiple parameters over single parameter, we compared the T_1ρ maps obtained by applying BCS, kt-PCA and CS schemes on the combined dataset (T_1ρ + T₂) and the T_1ρ only dataset.

Validation of the BCS algorithm using prospective 3D acquisition

The prospectively under sampled 3-D dataset is recovered using the BCS scheme. The dataset was undersampled on a Cartesian grid with a acceleration factor of R=8 using the under-sampling scheme 2. Each of the 128 slices in the dataset are recovered independently using BCS. The parameter maps are estimated from the pixels by fitting the mono-exponential model to the data. The MSE metric could not be used for the 3D experiments as the fully-sampled ground truth was not available. Hence, we determine the regularization parameter λ using the L-curve strategy (38).

RESULTS

Fully sampled 2D Acquisition

The comparisons of the two under-sampling patterns at acceleration factor of 8 is shown in Fig. 2. The MSE values and the error images in third column show that sampling scheme 2 (shown in Fig. 2(b)) provides better reconstructions. Sampling scheme 2 samples outer k-space more than sampling scheme 1 (shown in Fig. 2(a)), which reduces blurring of the high frequency edges. In other words, the sampling scheme 2 is both randomly and uniformly distributed in k-space making it suitable for multi-channel compressed sensing applications. The aliasing introduced by the 2×2 uniform grid in sampling scheme 2 is resolved using information from multiple coils. Using different sampling patterns for different frames increases incoherency and thus helps in better reconstructions. We use sampling scheme 2 for all the subsequent experiments.

We demonstrate the choice of the parameters in BCS and k-t PCA schemes in Fig. 3 using 8 fold retrospectively under sampled data. The comparisons were done in two regimes: one where the subject was still, and one with head motion during part of the scan. In Fig. 3(a)&(b), we show the model approximation error as a function of number of non-zero coefficients per pixel while representing the 2D dataset without and with motion for BCS and kt-PCA using learned basis functions respectively. In case of BCS scheme, the basis functions learned from BCS reconstruction of 6-fold under-sampled data were used whereas in case of kt-PCA, basis functions estimated from center k-space of the fully sampled data were used. We observe that BCS provides better compression capabilities than kt-PCA. In other words, the model fitting error in BCS is lower with less number of non-zero coefficients per pixel as compared to kt-PCA. We observe from Fig. 3(c)&(d) that the better signal representation offered by BCS translates to better reconstruction. Specifically, the optimal number of non-zero coefficients that yield minimum reconstruction errors in the kt-PCA model (10 in case without motion and 14 for case with motion) is considerably higher than that of BCS model (≈4 in case without motion and ≈5 in case with motion).

Fig. 3.

Comparison of BCS and kt-PCA model representation: (a) and (b) show the model approximation error against the number of non-zero coefficients per pixel of BCS and kt-PCA without and with motion respectively. (c) and (d) show the reconstruction error against the average number of non-zero model coefficients per pixel of BCS and kt-PCA models on the 2D dataset without and with motion respectively. We observe that BCS gives better reconstructions with less number of non-zero model coefficients than kt-PCA both in case of with and without motion. In other words the degree of freedom of BCS is less than that of kt-PCA. BCS model gives better compression than kt-PCA model as seen from (a) & (b). Note: For (a)&(b), the basis functions in case of BCS were estimated from 6 fold under-sampled data and the basis functions of kt-PCA were estimated from center of k-space of the fully sampled data.

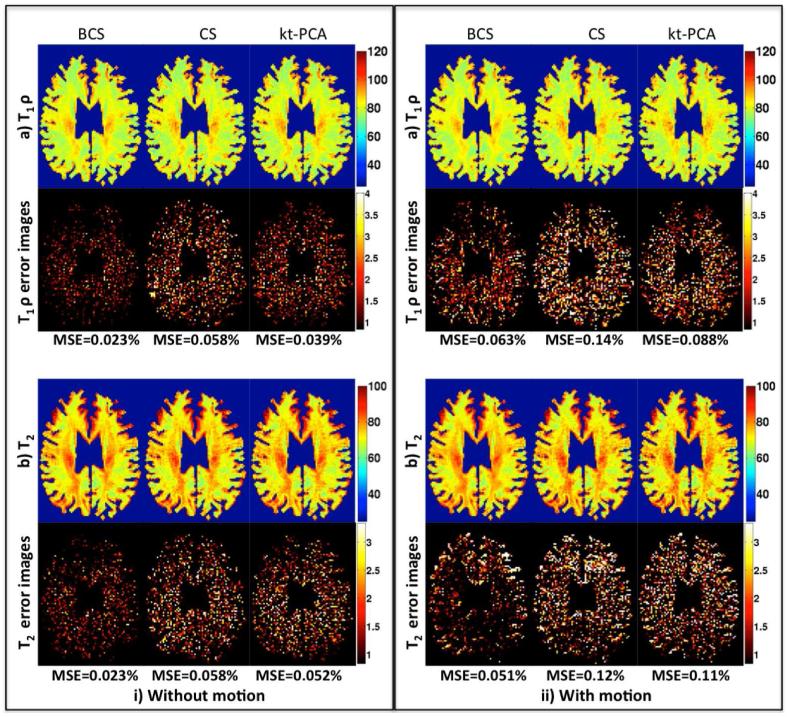
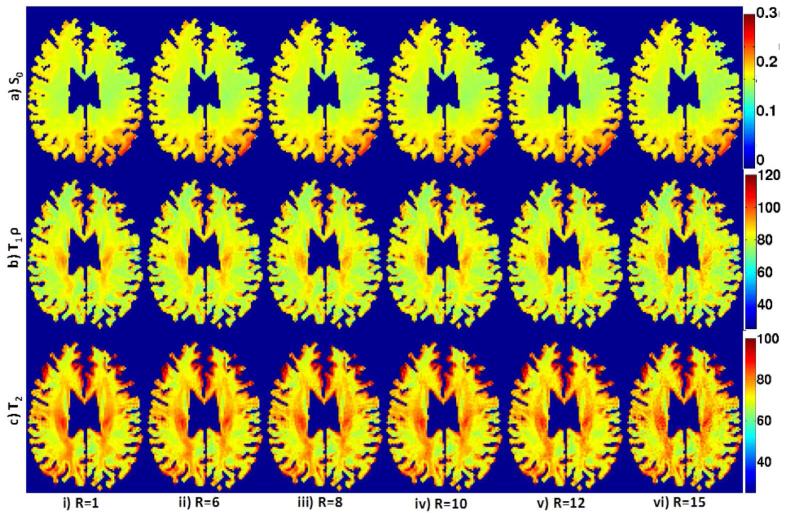
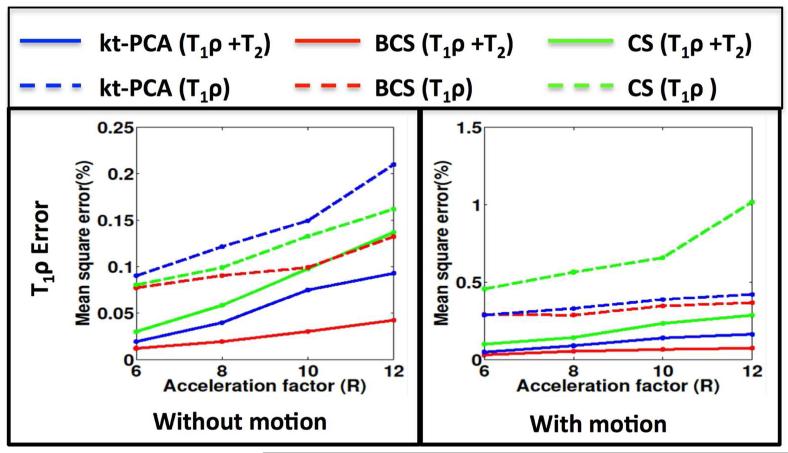
In Fig. 4, we compare the performance of BCS against k-t PCA scheme with and without sparsity constraint and CS schemes for different acceleration factors without motion (right) and in the presence of motion (left). We observe that BCS is capable of providing reconstructions with lower errors, compared with CS and k-t PCA schemes with and without sparsity constraint. The better performance of BCS in cases without and with motion can be attributed to the richer dictionary and lower degrees of freedom over other methods. The ℓ₁ norm on the coefficients and Frobenius norm constraint on the dictionary attenuate the insignificant basis functions which model the artifacts and noise as shown in Fig. 5(a) and thereby minimize noise amplification. In contrast, since the model order (number of non-zero coefficients) in kt-PCA without sparsity constraint is fixed a priori, basis functions modeling noise are also learned, especially in the case with motion. This is demonstrated in Fig. 5(c). Imposing a sparsity constraint on U in kt-PCA method improves the results over kt-PCA without regularization. This scheme can be seen as the first iteration of the BCS scheme. The results in the paper clearly demonstrate the benefit in re-estimating the basis functions. Specifically, the BCS scheme enables the learning of non-orthogonal basis functions, which provide sparser coefficients. The CS method on the other hand exhibited motion artifacts as the dictionary is learned from the data model which does not contain signal prototypes that account for patient-specific motion fluctuations. The comparison of T_1ρ and T₂ parameter maps at acceleration factor of 8 are shown in Fig. 6. We observe that BCS provides superior reconstructions which translate into better parameter maps as compared to other two schemes in both with and without motion datasets. Fig. 7 shows the parameter maps for different acceleration factors. Acceleration factors up to 15 were achieved with minimal degradation. All the schemes yield better T_1ρ maps in case of the combined (T_1ρ + T₂) dataset as compared to the only T_1ρ dataset as seen in Fig. 8. In addition, we observe that BCS gives better performance than other schemes, thus confirming that combining T_1ρ and T₂ datasets does not affect the reconstructions, instead it enables to achieve higher acceleration and improves the specificity of T_1ρ.

Fig. 5.

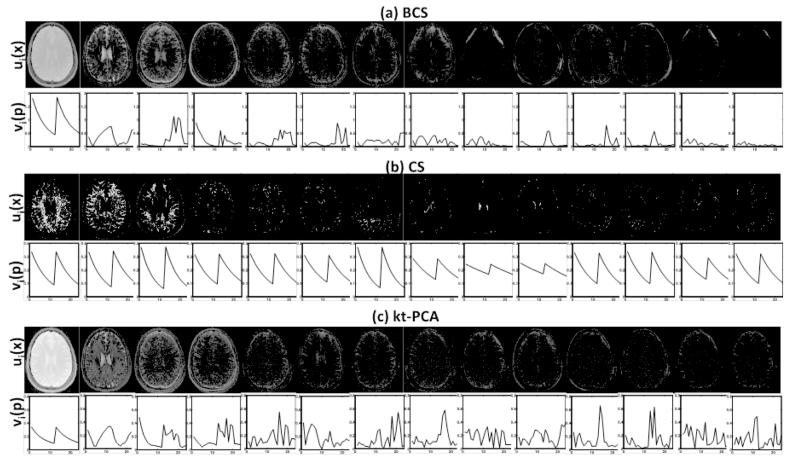
Model Coefficients and dictionary basis functions for the 2D data with motion: Few spatial coefficients u_i(x) and their corresponding basis functions v_i(p) for BCS, CS and kt-PCA schemes are shown in (a-c) respectively. The product entries u_i(x)v_i(p) are sorted according to Frobenius norm and first 14 entries are shown here. Since the Frobenius norm constraint attenuates the insignificant basis functions BCS reconstructions have less noise amplification whereas the basis functions estimated using kt-PCA scheme are noisy.

Fig. 6.

T_1ρ and T₂ parameter maps for retrospectively under-sampled 2D dataset: The T_1ρ and T₂ parameter maps obtained using BCS, CS and kt-PCA schemes on the 2D dataset with and without motion are shown in (i) and (ii) respectively. The maps are obtained at acceleration factor of 8. We observe that BCS scheme performs better than CS and kt-PCA schemes in both cases with and without motion. The noise in reconstructions using the kt-PCA and CS schemes propagates to the parameter maps and hence the degradation is higher in case of kt-PCA and CS as compared to BCS.

Fig. 7.

Parameter maps of a retrospectively under-sampled 2D dataset at different acceleration factors: S₀, T_1ρ and T₂ parameter maps (a-c) at acceleration factors R=1, 6, 8, 10, 12 and, 15 are shown in (i-vi). We observe reasonable reconstructions for acceleration factors up to 15 with minimal degradation in contrast.

Fig. 8.

Comparison of T_1ρ maps errors obtained from reconstructions of combined (T_1ρ + T₂) dataset and the T_1ρ only dataset: The T_1ρ maps errors at different accelerations for all the schemes on the combined dataset (solid lines) and only T_1ρ dataset (dotted lines) are shown. The plot on left shows comparisons for the datasets without any motion and the plot on the right shows comparisons for datasets with motion. We observe in both cases that BCS performs better than CS and kt-PCA schemes. In other words combining the datasets improves the reconstructions.

Prospective 3D Acquisition

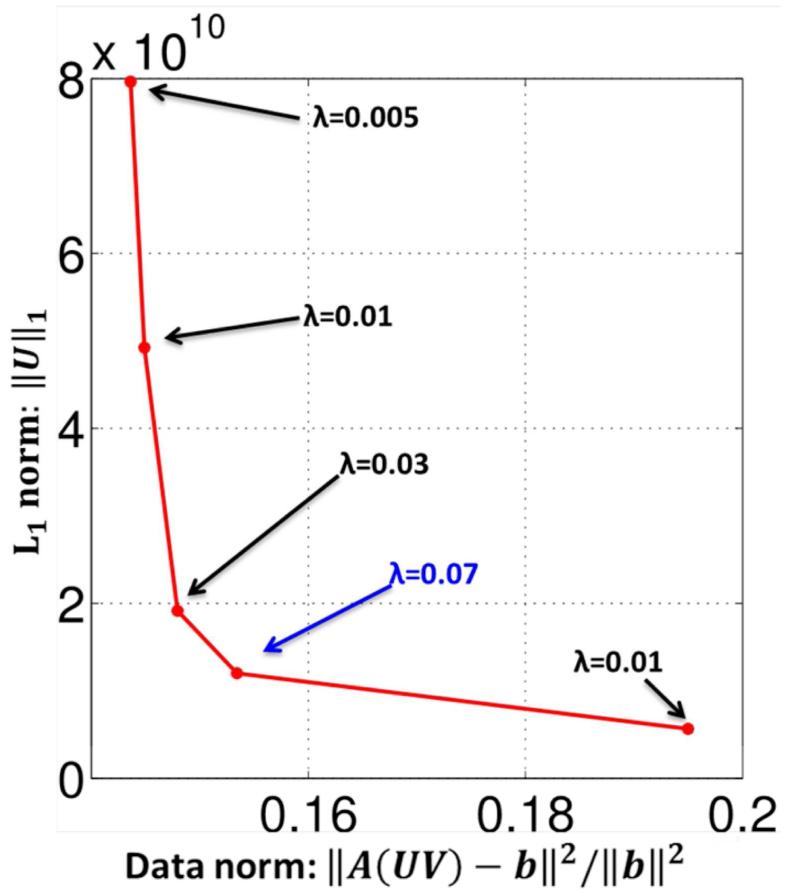
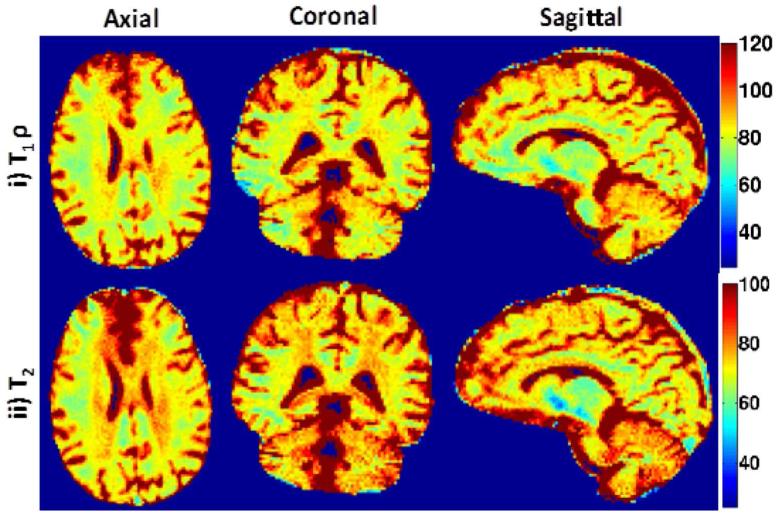
The optimal regularization parameter is chosen using the L- curve method as shown in Fig. 9. The λ value of 0.07 is then used to recover all the slices. The parameter maps for the prospectively under-sampled 3D dataset recovered using the BCS scheme are shown in Fig. 10. These results demonstrate that the BCS scheme yields good parameter maps with reasonable image quality. The acceleration factor of R=8 enables us to obtain reliable T_1ρ, T₂ and S₀ estimates from the entire brain within a reasonable scan time (20 min).

Fig. 9.

Choice of regularization parameter λ: The λ parameter was optimized using the L- curve strategy (38). We change λ and plot the data consistency error against the smoothness penalty. λ value of 0.07 was chosen as the regularizing parameter for the 3D dataset.

Fig. 10.

Parameter maps for 3D prospective under-sampled data at R=8: Axial, Coronal and Sagittal T_1ρ and T₂ parameter maps are shown in (i)-(ii). With the acceleration of R=8, the scan time was reduced to 20 min. Note: All 128 slices were processed slice by slice to reconstruct the 3D parameter maps

DISCUSSION

We have introduced a blind compressed sensing framework to accelerate multi-parameter mapping of the brain. The fundamental difference between CS schemes and the proposed framework is that BCS learns a dictionary to represent the signal, along with the sparse coefficients from the under-sampled data. This approach enables the proposed scheme to account for motion-induced signal variations. Since the number of different tissue types in the specimen is finite, this approach also enables use of smaller dictionaries, resulting in a computationally efficient algorithm. The main difference of the proposed scheme vs. k-t PCA scheme is the non-orthogonality of the basis functions and the sparsity of the coefficients. The richer model and the fewer degrees of freedom due to the sparsity of the coefficients translate to lower artifacts at high acceleration factors.

Since the kt-PCA basis functions are estimated from the center 9×9 kspace of the fully sampled data, it does not exploit the redundancy due to parallel MRI. The kt-PCA performance may be further improved by a pre-reconstruction step, where the missing k-space data is interpolated from the known samples using GRAPPA (39) or SPIRiT (40), prior to estimating the basis functions. However, no such pre-reconstruction is necessary in BCS since the dictionary is updated iteratively with the coefficients in the reconstruction process. The kt-PCA reconstructions, specially in presence of motion can be improved by using the model consistency condition (MOCCO) technique (41) introduced recently. Such a model consistency relaxation could also be realized with the BCS model, which is yet to explored.

Our comparisons with kt-PCA and CS schemes in the case of subjects experiencing head motion shows that BCS is more robust to motion. This behavior can be attributed to the ability of the BCS scheme to learn complex basis functions that capture the motion-induced signal variations. The ability to be robust to motion induced signal variations is especially important in high-resolution whole-brain parameter mapping experiments, where the acquisition time can be significant.

Based on our work that combined low-rank and spatial smoothness priors (28), we observed that the use of spatial smoothness priors along with low-rank priors as in Zhao et. al, ISMRM, 2012 can provide better reconstructions. While spatial smoothness priors can be additionally included with BCS to improve performance, this is beyond the scope of this paper.

The proposed method can only compensate for inter-frame motion. We correct for the motion using registration of the images in the time series, prior to estimation of the parameter maps. An alternative to this approach is the joint estimation of motion and the low-rank dataset as in (42). The improvement in the results comes from superior reconstruction of the image series, which translates into good quality parameter maps.

The quality of the reconstructions depends on the regularization parameter λ. We used the L-curve method to optimize λ. We observed that the value of λ did not vary much across different datasets acquired with the same protocol. Therefore, in the practical setting, once the λ is tuned for one dataset, it could be used to recover other datasets that are acquired using the same protocol. In order for the majorize-minimize algorithm to converge, β should tend to infinity, and convergence of the algorithm is slow at higher values of β. Thus the continuation method plays a significant role in providing faster convergence. Currently, the reconstruction time for one slice is about 40 min on the GPU. We observed that the CG steps required to solve the quadratic sub-problems are time consuming. These CG steps can be avoided by additional variable splitting in the data consistency term as shown in (43, 44), which is a subject of further investigation.

The proposed scheme can be extended in several directions. First, in the current setting, we reconstruct the 3D data slice by slice, but the algorithm can be further modified to reconstruct the entire 3D data at once, thus exploiting the redundancies across slices. However, this will be computationally expensive. Second, additional constraints such as total variation penalty on the coefficients and sparsity of the basis functions (45) can be added to further improve the results. Third, spatial patches can be used to construct dictionaries to exploit the redundancies in the spatial domain (46, 47). Lastly, we use a single exponential model to estimate the parameter maps. However several other models like multi-exponential model (48) which will accommodate for partial volume effects or a Bloch equation simulation based approach can be used for parameter fitting. Since, these extensions are beyond the scope of this paper, we plan to investigate these in future.

CONCLUSION

We introduced a blind compressed sensing framework, which learns an over-complete dictionary and sparse coefficients from under-sampled data, to accelerate MR multi-parameter brain mapping. The proposed scheme yields reasonable parameter estimates at high acceleration factors, thereby considerably reducing scan time. The robustness of the BCS scheme to motion makes it well suited for multi-parameter mapping in a setting with high probability of patient-specific motion or in a dynamic setting like in cardiac applications.