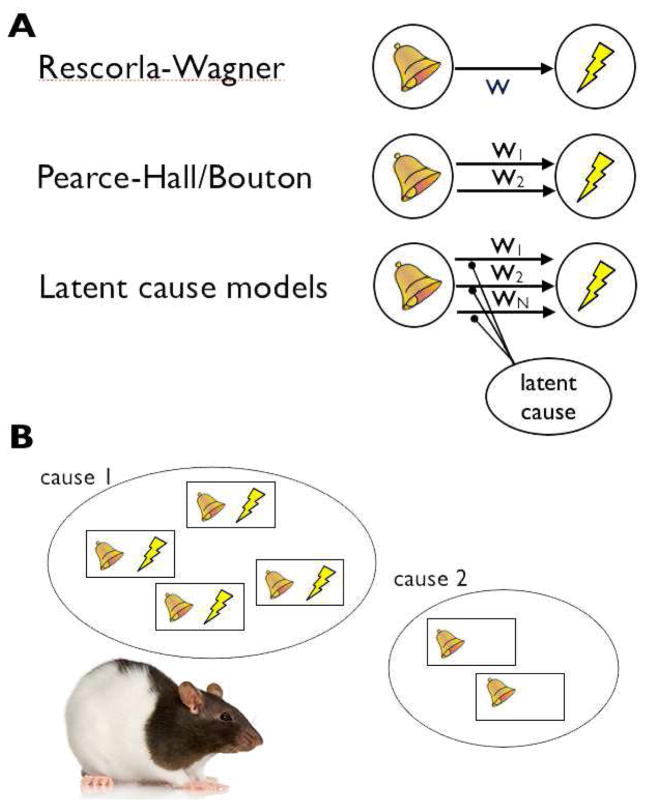
Figure 1. Simplified illustration of theoretical models of extinction.

Different theoretical models of associative learning imply different processes in extinction. A. In the Rescorla-Wagner model (top), associative weights (w) between CSs and USs can increase and decrease based on prediction errors. Here acquisition involves a neutral weight (w=0) acquiring value (e.g., w = 1) over time. Extinction in this model causes ‘unlearning’ as the negative prediction errors due to the omission of the expected US decrease w back to zero. In contrast, in the Pearce-Hall or Bouton models (middle), extinction training causes learning of a new association, here denoted by a new weight w₂ that predicts the absence of the US. Thus extinction does not erase the value that w₁ acquired during the original training. The latent cause model (bottom) formalizes and extends this latter idea—here multiple associations (denoted by the arbitrary number N) can exist between a CS and a US, and inference about which latent cause is currently active affects how learning from the prediction error is distributed among these associations. In particular, the theory specifies the statistical conditions under which a new association (weight) is formed, and how learning on each trial is distributed among all existing weights. B. Another way to view the latent cause framework is as imposing a clustering of trials, before applying learning. Similar trials are clustered together (i.e., attributed to the same latent cause), and learning of weights occurs within a latent cause (that is, each latent cause has its own weight). Note that while the illustration suggests that each trial (tone and shock, or tone alone) resides in one cluster only, this is an oversimplification. In practice, the model assigns trials to latent causes probabilistically (e.g., 90% to cause 1 and 10% to cause 2). Since on every trial there is some probability that a new latent cause has become active, the total number of clusters is equal to the number of trials so far; however, many clusters are effectively empty.