Abstract
Purpose:
X-ray computed tomography (CT) is widely used, both clinically and preclinically, for fast, high-resolution anatomic imaging; however, compelling opportunities exist to expand its use in functional imaging applications. For instance, spectral information combined with nanoparticle contrast agents enables quantification of tissue perfusion levels, while temporal information details cardiac and respiratory dynamics. The authors propose and demonstrate a projection acquisition and reconstruction strategy for 5D CT (3D + dual energy + time) which recovers spectral and temporal information without substantially increasing radiation dose or sampling time relative to anatomic imaging protocols.
Methods:
The authors approach the 5D reconstruction problem within the framework of low-rank and sparse matrix decomposition. Unlike previous work on rank-sparsity constrained CT reconstruction, the authors establish an explicit rank-sparse signal model to describe the spectral and temporal dimensions. The spectral dimension is represented as a well-sampled time and energy averaged image plus regularly undersampled principal components describing the spectral contrast. The temporal dimension is represented as the same time and energy averaged reconstruction plus contiguous, spatially sparse, and irregularly sampled temporal contrast images. Using a nonlinear, image domain filtration approach, the authors refer to as rank-sparse kernel regression, the authors transfer image structure from the well-sampled time and energy averaged reconstruction to the spectral and temporal contrast images. This regularization strategy strictly constrains the reconstruction problem while approximately separating the temporal and spectral dimensions. Separability results in a highly compressed representation for the 5D data in which projections are shared between the temporal and spectral reconstruction subproblems, enabling substantial undersampling. The authors solved the 5D reconstruction problem using the split Bregman method and GPU-based implementations of backprojection, reprojection, and kernel regression. Using a preclinical mouse model, the authors apply the proposed algorithm to study myocardial injury following radiation treatment of breast cancer.
Results:
Quantitative 5D simulations are performed using the MOBY mouse phantom. Twenty data sets (ten cardiac phases, two energies) are reconstructed with 88 μm, isotropic voxels from 450 total projections acquired over a single 360° rotation. In vivo 5D myocardial injury data sets acquired in two mice injected with gold and iodine nanoparticles are also reconstructed with 20 data sets per mouse using the same acquisition parameters (dose: ∼60 mGy). For both the simulations and the in vivo data, the reconstruction quality is sufficient to perform material decomposition into gold and iodine maps to localize the extent of myocardial injury (gold accumulation) and to measure cardiac functional metrics (vascular iodine). Their 5D CT imaging protocol represents a 95% reduction in radiation dose per cardiac phase and energy and a 40-fold decrease in projection sampling time relative to their standard imaging protocol.
Conclusions:
Their 5D CT data acquisition and reconstruction protocol efficiently exploits the rank-sparse nature of spectral and temporal CT data to provide high-fidelity reconstruction results without increased radiation dose or sampling time.
Keywords: 4D CT, spectral CT, microCT, retrospective gating, rank-sparsity
1. INTRODUCTION
X-ray computed tomography (CT) is ubiquitous, both clinically and preclinically, for fast, high-resolution anatomic imaging. However, compelling opportunities exist to expand its use in functional imaging applications by exploring the spectral and temporal dimensions. The simplest implementation of spectral CT, dual-energy (DE) CT, scans the same subject with two different x-ray spectra, allowing separation of two materials. We have demonstrated preclinical, functional imaging applications of DE-CT to separate iodine and calcium or iodine and gold nanoparticles, including classification of atherosclerotic plaque composition,1 noninvasive measurement of lung2 and myocardial perfusion,3 and the classification of tumor aggressiveness and response to therapy in primary lung cancers4 and in primary sarcomas.5,6 Our group has also pioneered preclinical 4D (3D + time) cardiac and perfusion imaging.7–10 Other groups have designed and implemented algorithms for 4D cardiac microCT using retrospective, cardiorespiratory projection gating.11,12
Binning retrospectively gated projections to cardiac phases results in random angular undersampling. The reconstruction problem for each cardiac phase is very poorly conditioned, requiring high-fidelity regularization to minimize variability in the results. Two primary strategies exist for regularizing reconstructions from binned projection data: spatiotemporal total variation (4D-TV)13 and prior image constrained compressed sensing (PICCS).14 4D-TV enforces spatiotemporal gradient sparsity between the reconstructions of adjacent cardiac phases, resulting in piecewise constant reconstruction results that are consistent in time. PICCS enforces gradient sparsity relative to a prior reconstruction, such as a well-sampled temporal average reconstruction, recognizing that most image features are static (redundant) in time. A third technique, robust principal component analysis,15 effectively combines redundancy (i.e., low rank) and sparsity constraints within a single framework. Algorithms for rank-sparsity constrained spectral16 and temporal17 CT reconstruction have been derived and demonstrated in simulations.
The novelty in the work presented here comes from a synergy between a hierarchical projection sampling strategy, a deterministic rank and sparsity pattern, and a regularization approach which exploits both, enabling simultaneous temporal and spectral CT reconstructions of in vivo data while maintaining or even lowering the associated radiation dose. In a preliminary investigation of this problem, we work with dual-energy microCT of the mouse combined with retrospectively gated cardiac CT. While the results we present use dual-energy CT exclusively to emphasize that the majority of our approach extends to an arbitrary number of spectral samples (i.e., >2),18,19 we call our combination of spectral and temporal CT reconstructions 5D CT. High-fidelity 5D CT reconstruction can reveal the dynamic range of cardiac and respiratory motion (temporal contrast) in the context of information such as vascular density and perfusion quantified by the concentrations of spectrally differentiable contrast agents (spectral contrast and material decomposition).
As a motivating example, we apply our low-dose 5D CT imaging and reconstruction protocol to study myocardial injury following radiation therapy (RT). RT can be combined with surgery to treat breast cancer, improving rates of local control, and for some subgroups of patients, rates of survival.20,21 However, RT to the chest, which includes exposure of the heart to radiation, can cause radiation-related heart disease (RRHD) and death.20,22–25 Radiation dose to the heart has been reported to correlate with the risk of RRHD,25 though identifying patients who will develop RRHD remains challenging.
In a previous microCT study of myocardial injury following partial heart irradiation in a mouse model,26 CT data were acquired 4 and 8 weeks after 12 Gy partial heart irradiation. An additional microSPECT scan was acquired following the 8-week time point. Concerns over potential compounding effects between the treatment dose and the imaging doses constrained the CT data acquisition protocol. Specifically, instead of acquiring a full prospective data set at two energies (dose: ∼1300 mGy), a single prospectively gated data set was acquired with dual energy (dose: ∼130 mGy) to allow accurate measurement of perfusion defect (myocardial injury) size and extent based on its accumulation of gold nanoparticles. A second, somewhat lower quality, retrospectively gated 4D (3D + time) data set was acquired to enable quantification of left ventricle functional metrics (dose: ∼290 mGy). While the total dose associated with these two image acquisitions was a fraction of the total dose associated with a prospectively gated 5D acquisition (1300 vs 420 mGy), the two acquired data sets were highly redundant.
This scenario raises questions regarding the expectation of reliable material decomposition results and high temporal resolution from a predetermined amount of retrospectively gated projection data. More specifically, if we are willing to take on the computational burden associated with solving several iterative reconstruction problems in tandem, can we exploit the redundancy between each phase and energy to greatly reduce the amount of projection data and the scanning time required for reliable 5D reconstruction results? Using the methods proposed in Sec. 2, we believe the answer is yes.
2. METHODS
To develop the proposed algorithm for 5D CT reconstruction, the general rank-sparse signal model and its application to CT reconstruction are first presented (Secs. 2.A and 2.B). Data fidelity constraints enforced by residual weighting are then outlined (Sec. 2.C). Methods and motivations for enforcing gradient sparsity and low rank via rank-sparse kernel regression (RSKR) are detailed in Secs. 2.D–2.F. The presented concepts are then related through pseudocode for the proposed algorithm (Sec. 2.G). Section 2.H discusses the example application, the investigation of cardiac injury following partial heart irradiation. Finally, details of simulation and in vivo experiments are presented in Secs. 2.I and 2.J.
2.A. Sparsity-constrained CT reconstruction
To set up the problem of rank-sparsity constrained CT reconstruction, we begin with a general expression for sparsity-constrained CT reconstruction,
| (1) |
In solving this problem, X, the proposed solution, is projected through the imaging system, A (AT, backprojection) and is compared with the system calibrated and log-transformed projection data, Y. The optimal solution minimizes the sum of these residuals and the absolute sum of intensity gradients in X as weighted by the regularization parameter, λ. Common choices for the gradient operator, W, include total variation27 and the piecewise-constant B-spline tight frame transform.28 Section 2.D details the gradient operator used in this work, bilateral total variation (BTV).
The matrix X consists of several columns, each representing the reconstructed result at a given temporal phase (t) and energy (e),
| (2) |
where NT is the total number of time points (cardiac phases) and NE is the total number of energies to be reconstructed. As each column of X represents an independent volume, the dimensions of X are the number of voxels per volume (rows) by time and energy (columns, NE ⋅ NT). When retrospective projection sampling is used (as it is here), Y consists of NE columns,
| (3) |
Each column of Y has NY rows (number of detector elements times the number of projections per energy). Given these definitions for X and Y, Eq. (1) is shorthand notation for a series of temporal and energy selective reconstruction problems,
| (4) |
Equivocating Eqs. (1) and (4), A and AT are defined to apply to all columns of X and Y independently, with the total cost being the summation of all temporal and energy selective costs. Furthermore, A and AT are energy selective (e subscript) to match the angular sampling of Ye. The time and energy selective, diagonal weighting matrix, Q, noted by an L2-norm subscript in Eq. (1), is the product of a weighted least squares penalty term and a time point selective weighting term. These weights are detailed in Sec. 2.C. Nominally, the gradient operator, W, is defined to apply to each column of X independently; however, within the context of joint, low rank and gradient sparsity constraints, enforcing regularity between the columns of X can be highly efficacious.
2.B. Rank-sparsity constrained CT reconstruction
To develop this joint regularization strategy, we begin by defining rank-sparse solutions to the CT reconstruction problem as those that adhere to the following signal model:
| (5) |
In other words, X is exactly represented as the sum of two matrices which have the same number of rows and columns as X: one with low column rank (XL) and one with sparse nonzero entries (XS). Low column rank implies that the number of independent columns of XL is less than its total number of columns.
Thanks to the work of Candès et al.,15 we know that if a meaningful rank-sparse decomposition exists, it can be very generally estimated through convex optimization (robust principal component analysis, RPCA),
| (6) |
subject to
‖XL‖* is referred to as the nuclear norm and represents the sum of singular values of the matrix XL. Minimizing this sum is a convex proxy for minimizing matrix rank. Similarly, the L1-norm is a convex proxy for enforcing gradient sparsity within the columns of XS.
Combining Eqs. (1) and (6) yields a new expression for rank-sparsity constrained CT reconstruction,
| (7) |
In other words, Eq. (7) expresses that we wish to find a reconstruction that is closely related to the acquired projection data and that has a rank-sparse decomposition. Depending on the projection sampling strategy and the rank and sparsity pattern of the columns of X, enforcing regularity on the rank-sparse decomposition of X in lieu of its independent columns can substantially improve the conditioning of the inverse problem. In Secs. 2.C–2.F, we discuss the specifics of our data fidelity weighting and regularization strategies for rank-sparsity constrained (5D) CT reconstruction. Following previously published work,16,29 we then solve a modified version of Eq. (7) using the split Bregman method and the add-residual-back strategy (Sec. 2.G).
2.C. Data fidelity weighting
The data fidelity residuals in Eqs. (1) and (7) are weighted by the time and energy selective diagonal matrix, Q. For our implementation of 5D CT reconstruction,
| (8) |
The Q matrix is, itself, the product of two diagonal matrices (each with dimension NY ⋅ NY): the time point (phase) selective matrix, T, and the energy selective matrix, Σ. Σ weights each individual line integral using a weighted least squares approach,30
| (9) |
| (10) |
where i indexes all detector pixels and projections acquired at a single energy (i.e., i = 1 : NY). The relationship between the measured projection data, Y, and the measurement variance, σ2, is modeled as Gaussian [Eq. (10)], given a constant parameter, η, relating the two. Physically, this relationship recognizes that highly attenuated measurements are the least reliable. Within the context of sparsity-constrained CT reconstruction [Eqs. (1) and (7)], highly attenuating features are more heavily regularized, while low contrast features are better resolved. We note that using a diagonal covariance matrix implies (assumes) that the projection measurements are spatially uncorrelated.
The temporal weights, T, are redundant for all line integrals within a single projection and are determined using Gaussian basis functions. The complete set of basis functions (here, 10) spans the R–R interval of the cardiac cycle. To reconstruct a given phase, a weight is assigned to each projection based on the normalized difference between the time point to be reconstructed and the time at which each projection was acquired. Once assigned, the weights for each phase are normalized such that they sum to one. Given these weights, enforcing data fidelity for a given cardiac phase amounts to interpolating the reconstruction of that phase from among the acquired temporal samples. More details on the computation of the temporal weights are provided in Subsection 1 of the Appendix.
Further regarding temporal weighting and the work presented here, we assume that the temporal sampling is only loosely correlated with projection angle and cardiac phase so that the overall sampling pattern is effectively random. This assumption holds true for the in vivo results presented here (Sec. 2.J); however, additional delays in the projection acquisition sequence may be required to decorrelate temporal samples in future work. To deal with respiratory motion in the in vivo data, the respiratory cycle was retrospectively divided into ten phases of equal length (starting and ending at end inspiration). Projections acquired during the outlying respiratory phases (8 and 9) were given a temporal weight of zero prior to normalization of the temporal weights. Additional details of the respiratory gating are provided in Sec. 2.J.
2.D. Bilateral total variation
For the proposed 5D reconstruction algorithm, we use bilateral filtration (BF) to enforce image domain, intensity gradient sparsity. The bilateral filter is an edge-preserving, smoothing filter,31
| (11) |
As before, Xt,e denotes the column of X corresponding to time point t and energy e, while dt,e denotes the corresponding filtered result. The variable l indexes the voxel within Xt,e to which the filter is applied. The variable m indexes a complete set of 3D voxel offsets from l at which filtration weights are computed to perform weighted averaging. Combined represents the image intensity at position l − m within reconstructed volume Xt,e. Specific to our implementation of BF,18 the domain (D) and range (R) kernels used to compute the filtration weights are defined as follows:
| (12) |
| (13) |
The filtration domain [Eq. (12)] is spatially invariant, depending only on the position offset. The domain radius, b, defines the scales of image derivatives given equal, nonzero weight within the filtration domain (here, b = 6). The Gaussian range weights [Eq. (13)] are scaled by a user-defined scalar multiplier, h, which controls the degree of smoothing (h ≈ 2.5), and the noise standard deviation, σt,e, measured in Xt,e prior to filtration.
In the original implementation of BF from the work of Tomasi and Manduchi,31 the range weights are centered on the intensity of the voxel being filtered,
| (14) |
Notably, this is also a generic definition for the intensity gradient operator referred to in the sparsity-constrained CT reconstruction problem [Eqs. (1) and (7)]. However, we have previously demonstrated that resampling Xt,e to the 10% cutoff of the modulation transfer function of the imaging system greatly improves denoising performance without substantially compromising image resolution,6 leading to a modified definition specific to our implementation of BF,
| (15) |
The K subscript of W denotes that the filtration domain is resampled with a spatially invariant, 2nd order, classic kernel,6,32 denoted by K, prior to the computation of the intensity gradient. The n index is equivalent to, but independent of, m.
Building on a previous derivation33 and practical applications,18,34 it can be shown that BF reduces BTV subject to data fidelity,
| (16) |
| (17) |
As with Eqs. (1) and (7), the columnwise evaluation of Eq. (16) is implied. Additional details on the origins of Eqs. (16) and (17) can be found in Subsection 3 of the Appendix. The significance of Eq. (16) to the problem of 5D CT reconstruction and the split Bregman method will be discussed in Secs. 2.F and 2.G. Here, we compare Eq. (11) (BF) and 17 (BTV) and see that BTV applies the BF weights to the magnitude of the intensity gradients. Summing over all spatial positions (l), energies (e), and time points (t) yields the cost associated with BTV.
Enforcing gradient sparsity with BTV provides several specific advantages over total variation based approaches. Much like the B-spline tight frame transform, BTV considers multiple scales of image derivatives, minimizing gradients between distant neighbors and, potentially, preventing over smoothing relative to localized total variation.34 Unlike tight frame transforms, however, BTV abstracts image intensities to probabilities in the form of spatially localized range weights. When several images share the same underlying image structure, weights at the same spatial position in each image can be multiplied to substantially improve denoising performance in each individual image, regardless of differences in or lack of image contrast. We have previously applied this approach for postreconstruction denoising of spectral CT data.18 We call this approach joint bilateral filtration (joint BF) because it treats the intensity in each spectral dimension as an independent (jointly) Gaussian random variable,
| (18) |
where n is a generic index for N total volumes. The resulting range kernel, , replaces in Eq. (11) for the filtration of each component volume, reducing BTV in a way that promotes consistency between each component image and greatly improving the fidelity of postreconstruction material decomposition.18
For temporal reconstruction, we further extend the minimization of BTV to the temporal dimension. Specifically, we extend the image domain by one cardiac phase preceding and following the cardiac phase to which the filter is being applied (Sec. 2.F). Given the inherent edge-preserving nature of the bilateral filter, temporal “edges” are preserved between cardiac phases based on the assigned range weights. Note that we are not the first to apply bilateral filtration to the problem spatiotemporal CT reconstruction;35 however, we are the first to integrate it into the split Bregman method for explicit minimization of BTV (Sec. 2.G).
2.E. Rank-sparse signal model
Sections 2.A and 2.B reviewed the application of RPCA to CT reconstruction based on previous work.16 In Sec. 2.D, we reviewed our own contrast and noise independent scheme for enforcing image-domain gradient sparsity. In Secs. 2.E and 2.F, we combine the robustness of rank-sparse representation with the joint regularity enforced by BF to create a new regularization strategy we refer to as RSKR.
We begin by noting that, despite its ease of application, RPCA can require tens or even hundreds of singular value decomposition operations to converge to an exact solution, limiting its practicality in real-world CT reconstruction problems. Luckily, by exploiting additional constraints inherent in the problems of temporal and spectral CT reconstruction, we can take advantage of rank-sparse representation without explicitly performing RPCA. Said in another way, if we know, a priori, what rank and sparsity pattern to expect, we can regularize the reconstruction problem in such a way that the solution adheres to the expected pattern.
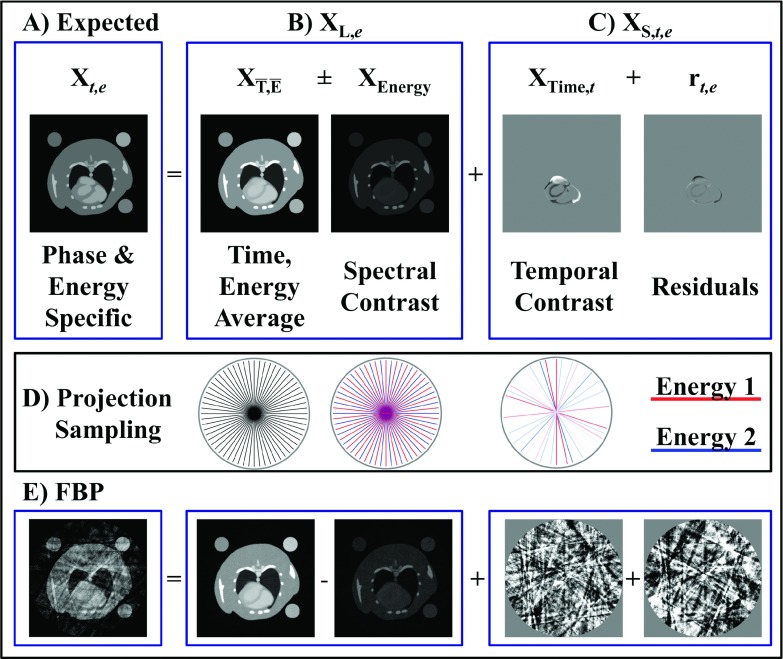
For the sample problem of dual energy reconstruction (NE = 2) at 10 time points (NT = 10), we model the reconstruction at a given phase and energy, Xt,e, as the sum of the following components (Fig. 1):
| (19) |
The second expression relates Xt,e to the general rank-sparse signal model [Eq. (5)]. This problem specific variant of the rank-sparse signal model highlights that the NT ⋅ NE columns of X are described by a low-rank basis, XL,e, which depends on energy, and spatially sparse components, which depend on both time and energy, XS,t,e. is shorthand notation for the time () and energy () average reconstruction which consists of a single column,
| (20) |
When reconstructed from angularly interleaved spectral projection data acquired over a full rotation, represents a high-fidelity reconstruction with minimal undersampling artifacts, even when each individual energy is angularly undersampled. For the case of dual energy, the spectral contrast, XEnergy, is then a single column,
| (21) |
where is the temporal average reconstruction at energy 1. In relation to the general rank-sparse decomposition [Eq. (5)] and the definition of X in Eq. (2), the spectral dimension is then represented as follows for the dual energy case:
| (22) |
XL,e=1 and XL,e=2 represent the static portions of the volume at each energy and form a rank 2 basis for approximating all NT ⋅ NE columns of X.
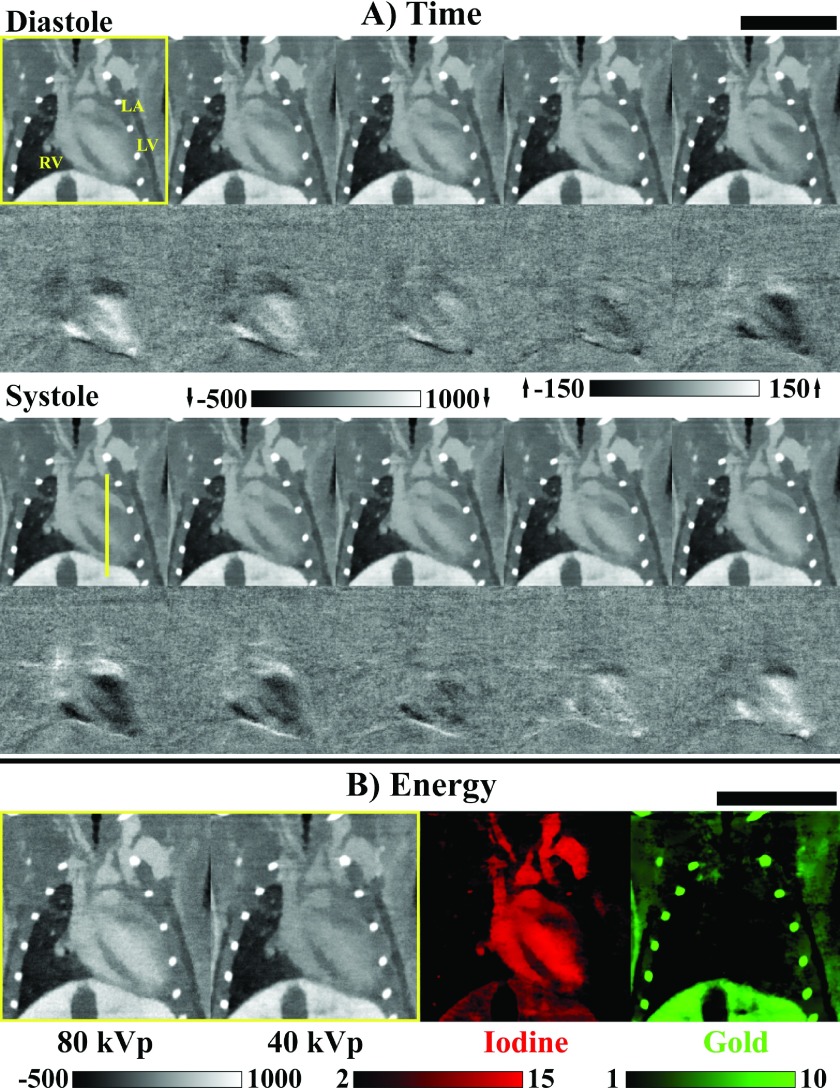
FIG. 1.
Rank-sparse signal model. (A) The expected reconstruction at a given time point and energy, Xt,e, is modeled as the sum of low-rank basis functions describing the energy dimension, XL,e, and sparse columns describing the spectrotemporal contrast, XS,t,e [Eq. (19)]. The independent columns of XL,e are chosen to correspond with the time and energy average reconstructions () and the spectral (“energy”) contrast (XEnergy). The sparse columns of XS represent the temporal contrast (XTime) and additional energy-dependent spectrotemporal contrast (rt,e). For dual energy CT using energy integrating detectors, the magnitude of rt,e is comparatively small, leading to a separable approximation by which the time and energy dimensions are regularized independently [Eq. (25)]. (D) The average reconstruction is regularly and densely sampled. The energy dimension is deterministically undersampled, while the time dimension is randomly sampled (projection intensity ∝ assigned weights). (E) Projection undersampling leads to noise and shading artifacts in FBP reconstructions; however, complementary image structure between each component can be exploited for high-fidelity regularization.
By definition, XL,e=1 and XL,e=2 [Eq. (22)] are simply the time average reconstructions at each energy (i.e., ); however, within the context of RSKR, stratifying noise and undersampling artifacts to XEnergy will prove significant (Sec. 2.F). Beyond dual energy, decomposition of into and XEnergy can be generalized to an arbitrary number of energies by performing principal component decomposition of , increasing the number of columns of XEnergy to NE − 1. Singular value decomposition to find principal components seems inefficient given the previous observation that RPCA may be impractical for real-world CT reconstruction problems. Here, however, the energy dimension will generally be much smaller than the dimensionality of X (i.e., NE < NT ⋅ NE), reducing computation time. Furthermore, the proposed algorithm converges after a very small number of regularization steps (Sec. 3.C). We discuss future adaptation of the proposed model to an arbitrary number of energies in Sec. 4.
Similar to the spectral contrast, the temporal contrast, XTime, is computed as follows:
| (23) |
where is the energy average reconstruction at time point t. The NT total columns of XTime are energy independent. The temporal contrast is included in the NT ⋅ NE columns of XS in the general rank-sparse signal model [Eq. (5)],
| (24) |
Referring back to Eq. (19), the only time and energy dependent component is the spectrotemporal contrast, rt,e, which represents the residual in approximating Xt,e as the sum of separable time (XTime) and energy (, XEnergy) components. Figure 1 illustrates each component of our problem specific, rank-sparse signal model.
2.F. Rank-sparse kernel regression
Given retrospective projection sampling along the time dimension, the problem of reconstructing each phase of the cardiac cycle at each energy is poorly conditioned. To overcome this poor conditioning, our implementation of RSKR approximates each column of Xt,e using only its separable components (Fig. 1),
| (25) |
The extent to which this separable approximation holds informs the potential for projection undersampling in solving the 5D reconstruction problem, since the same projections are used to solve two separate subproblems. Separability also partially alleviates poor conditioning, since the temporal contrast is recovered using angularly interleaved projections from each sampled energy.
Despite these features, substantial regularization is still required to minimize variability in reconstructions from undersampled, retrospectively gated projection data. To this end, RSKR exploits the well-sampled time and energy average reconstruction () as a template for regularizing energy and time resolved reconstructions within the framework of joint BF [Eq. (18)]. Specifically, to regularize the spectral contrast, the following joint BF operation is performed,
| (26) |
BF() is shorthand for joint filtration between and each column of XEnergy, and and dEnergy are defined as the filtered analogs of and XEnergy, respectively. For the dual energy case where XEnergy is a single column, Eq. (26) is equivalent to the following evaluated at all voxel coordinates, l,
| (27) |
| (28) |
In other words, a single joint range kernel, , is computed [Eq. (28)] and then used to filter each column of the input [Eq. (27)]. Because is well sampled compared with XEnergy, the range weights associated with primarily determine the joint range weights (), and the image structure is copied from to the columns of XEnergy while preserving the contrast in XEnergy. After applying the filter, the regularized, low-rank components are recovered as follows for the dual energy case:
| (29) |
Because of the complementary structure enforced between each component, and dEnergy add (subtract) constructively in recovering dL,e. In the multienergy case, dL would be recovered from , the filtered principal components (i.e., filtered columns of dEnergy) and the component coefficients. For convenience, we denote the factorization of X into [Eq. (20)] and XEnergy [Eq. (21)], the application of the filter [Eq. (26)], the recovery of the filtered, low-rank components [Eq. (29)], and the replication of the low-rank components NT times to represent all NT ⋅ NE columns of X [Eq. (2)] as a single operation,
| (30) |
To regularize each component of the temporal contrast, the following joint filtration operation is performed at all voxel coordinates, l, and time points (columns of XTime), t,
| (31) |
| (32) |
Analogous to the spectral filtration operation, and XTime are used to construct the joint range kernel, RT [Eq. (32)], with the objective of copying image structure from to each column of XTime. Since is already computed in the spectral filtration operation and included in dL, only XTime is filtered with the joint kernel, yielding its regularized analog, dS [Eq. (31)]. Specific to the temporal filtration operation, the filtration domain is circularly extended along the time dimension to enforce spatiotemporal gradient sparsity between neighboring time points. To filter phase t, we choose to include one phase prior to the phase being filtered (q = t − 1) and one phase after the phase being filtered (q = t + 1) in addition to the phase being filtered (q = t). The voxel coordinates, l − m, are time point invariant, meaning that all voxels across time and space which are within the filtration domain contribute equally to the weighted average which updates the intensity of voxel l at time point t [Eq. (31)]. Given the extended domain, the gradient operator [Eq. (15)] is modified to the following:
| (33) |
In other words, only the time point being filtered, t, is resampled. The resampled intensity is then used to compute intensity differences within the extended filtration domain.
As with the spectral filtration operation [Eq. (30)], we define the following shorthand notation for the temporal filtration operation:
| (34) |
This notation represents factorization of X to and XTime [Eqs. (20) and (23)], joint filtration of and each column of XTime at each spatial location [Eq. (31) evaluated for all l], and replication of the filtered result NE times to match all NT ⋅ NE columns of X [Eq. (2)]. Because both the spectral and temporal contrast images are filtered relative to the same well-sampled time and energy average image [Eqs. (27) and (31)], they add constructively to form d, the regularized approximation of X,
| (35) |
Because of the separable approximation [Eq. (25)], we note that d does not include the regularized analog of the spectrotemporal contrast, r.
2.G. Rank-sparsity constrained 5D reconstruction
To perform 5D reconstruction, we revisit the equation for rank-sparsity constrained CT reconstruction [previously, Eq. (7)],
| (36) |
Following from our separable approximation [Eq. (25)], which enforces low-rank spectral contrast and sparse temporal contrast, we modify Eq. (36) to include BTV as reduced by the BFEnergy [Eq. (30)] and BFTime [Eq. (34)] filtration operations discussed in Sec. 2.F,
| (37) |
The subscripts Energy and Time denote the range weights for which BTV is reduced [RE, Eq. (28) and RT, Eq. (32)]. It is possible to minimize BTV for the time and energy dimensions independently; however, because the range weights are bounded by the same time and energy average range weights in both cases and because the data fidelity depends on the sum of both components, it is convenient (and effective) to combine them into a single expression,
| (38) |
Equation (38) is, in fact, a general expression for sparsity-constrained CT reconstruction which minimizes BTV [compare with Eq. (1)]. It is the choice of range weights and the factorization of X prior to regularization which change as a function of the dimensionality of the problem. In this way, Eq. (38) applies to rank-sparsity constrained 5D reconstruction as well as to any problems which include a subset of the space, time, and energy dimensions (e.g., 3D + time and 3D + energy).
Following previously published work, we solve Eq. (38) using the split Bregman method with the add-residual-back strategy.16,29 We replace the singular value thresholding (rank reduction) and soft thresholding (gradient sparsity) of the prior rank, intensity, and sparsity model [PRISM (Ref. 16)] with RSKR, obtaining a revised algorithm for rank-sparsity constrained spectrotemporal CT reconstruction (i.e., “5D reconstruction,” Fig. 2). Each L2-norm minimization subproblem (steps 1 and 8) is solved using the previously discussed data fidelity weighting (Sec. 2.C) and five iterations of the biconjugate gradient stabilized method.36 The minimization for each phase and energy in step 1 is initialized with unweighted filtered backprojection (FBP) using all available projection data acquired at the matching energy. The minimization for each phase and energy in step 8 is initialized with the result from step 1 (first iteration) or with the estimate from the previous iteration (subsequent iterations). As previously discussed, the algorithm readily handles the limiting cases of temporal reconstruction at a single energy and spectral reconstruction at a single time point. We note that the name kernel regression in our newly proposed regularization strategy, RSKR, is derived from the overlap between the add-residual-back strategy used with the split Bregman method29 and a denoising technique known as kernel regression,32 both of which iteratively refine the residuals associated with noise (v; Fig. 2, steps 3–6). Bilateral filtration with the reintroduction of residuals is a form of kernel regression for piecewise constant signals.32 A detailed derivation of the 5D reconstruction algorithm can be found in Subsection 2 of the Appendix.
FIG. 2.
5D CT reconstruction using the split Bregman method and rank-sparse kernel regression. (1) Weighted least squares initialization of each time point and energy to be reconstructed. Note that each column of X is updated independently [Eqs. (1) and (4)]. (2) Initialization of the regularization (v) and data fidelity (f) residual terms. (3–6) A single iteration of rank-sparse kernel regression (Sec. 2.F). (7 and 8) Data-fidelity updates for each time point and energy. Convergence of steps 3–8 is declared when the magnitude of the residual updates falls below a specified tolerance (∼3 iterations, Sec. 3.C). A detailed derivation of this algorithm can be found in Subsection 2 of the Appendix.
In the case of spectral CT reconstruction, we use the reconstructed results at each energy to perform postreconstruction material decomposition,
| (39) |
M is a system calibrated and optimized material sensitivity matrix which converts between material concentrations, C, and x-ray attenuation, X. Because material concentrations cannot be negative, an additional non-negativity constraint (C ≥ 0) is enforced by performing subspace projection on the least squares decomposition of each image voxel. We have detailed our material decomposition approach in previous work.18 As discussed in this previous work, an approximation is required to separate two exogenous contrast agents using dual energy data. Tissues denser than water (e.g., muscle) appear to be composed of low concentrations of the two contrast materials; however, these concentrations are generally lower than the sensitivity of the decomposition method and can be factored out by windowing for visualization (used for the in vivo data here, Sec. 2.J) and by subtracting out the apparent tissue concentrations when making quantitative measurements. Bone appears to be composed of gold, but can easily be ignored or segmented out as needed. While not performed here, we note that projection-based beam hardening correction prior to reconstruction could improve material decomposition accuracy.
2.H. Cardiac injury data
To illustrate the potential of our newly proposed spectrotemporal CT reconstruction scheme, we revisit the study outlined in Sec. 1. This previous study used cardiac microCT to assess a preclinical model of cardiac injury following radiotherapy (12 Gy partial heart irradiation).26 The study concluded that Tie2Cre; p53FL/− mice with both alleles of p53 deleted in endothelial cells developed substantial myocardial perfusion defects and left ventricle hypertrophy within 8 weeks of partial heart irradiation, while Tie2Cre; p53FL/+ mice with a working copy of p53 did not. Furthermore, a highly significant correlation (p = 0.001) was established between the accumulation of gold nanoparticles within the myocardium assessed by dual energy microCT and perfusion defects within the myocardium measured with microSPECT.
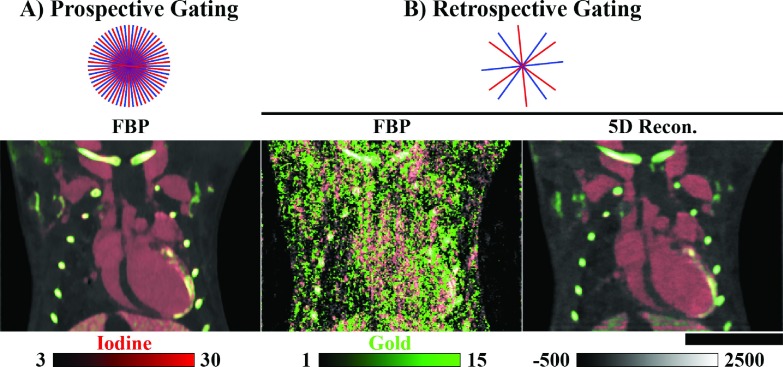
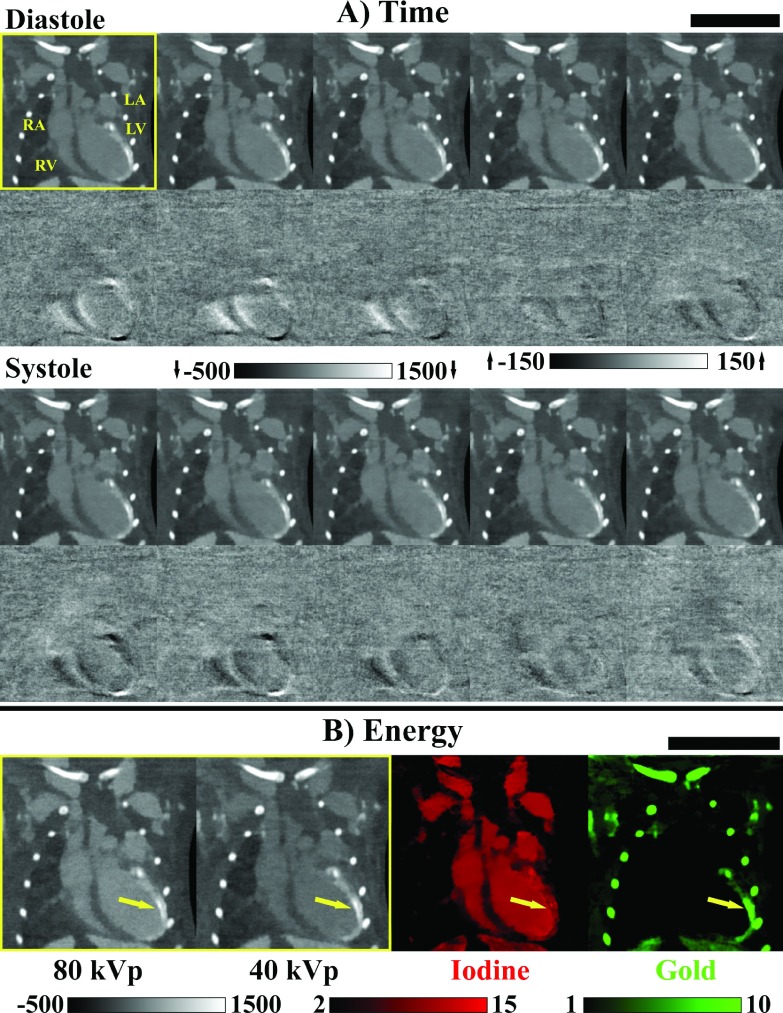
Representing these previous findings, the imaging results presented here were acquired 4 (Tie2Cre; p53FL/+) and 8 (Tie2Cre; p53FL/−) weeks after partial heart irradiation. Three days prior to imaging, gold nanoparticles were injected into the vasculature (0.004 ml/g AuroVist; Nanoprobes, Yaphank, NY). Three days was adequate for these nanoparticles to accumulate at the site of myocardial injury and then to clear from the vasculature. Immediately prior to imaging, liposomal iodine nanoparticles37 were injected into the vasculature (0.012 ml/g) to allow measurement of cardiac functional metrics. Figure 3 compares prospectively gated in vivo microCT data used in this previous study (A) with a weighted filtered backprojection reconstruction of a second set of retrospectively gated projection data used in this paper (B). A single phase (ventricular diastole) was imaged using prospective gating and regular angular sampling (300 projections/energy). Additional data acquisitions details are provided in Sec. 2.J.
FIG. 3.
Prospective vs retrospective projection gating. (A) Results of in vivo dual energy microCT reconstruction in the mouse. Three hundred projections were acquired at each of two energies (80 kVp, shown; 40 kVp) using prospective cardiorespiratory gating [end diastole, 300 projections/energy/phase] (Ref. 26). Reconstruction of each data set was performed using FBP followed by joint BF prior to material decomposition (red, iodine; green, gold). (B) Comparable reconstruction results using retrospective projection gating followed by time-weighted FBP (Sec. 2.C) and by 5D reconstruction with rank-sparse kernel regression [22.5 projections/energy/phase; Fig. 2]. Approximate relative projection sampling densities are as shown by energy for one cardiac phase and for dual source acquisition. Iodine and gold concentrations are shown in mg/ml. CT data are scaled in Hounsfield units. Scale bar: 1 cm.
2.I. Simulations
To validate the convergence of the proposed algorithm given random temporal sampling and to illustrate the effectiveness of RSKR, we conducted a 5D cone-beam CT simulation experiment using our dual source system geometry38 and realistic spectral and noise models. Mimicking the cardiac injury model discussed in Sec. 2.H, the MOBY mouse phantom39 (400 × 400 × 160, 88 μm, isotropic voxels) was modified to include 3 mg/ml of gold in the myocardium and 12 mg/ml of iodine in the blood pool. The simulation experiment included data acquired at two energies (40 and 80 kVp; tungsten anode; filtration: 0.7 mm Al and 3 mm PMMA), allowing postreconstruction material decomposition of iodine and gold [Eq. (39)]. Identical to the in vivo data discussed in Sec. 2.J, the simulation was initialized with 225 projections/energy with interleaved regular angular sampling over a single 360° rotation [Fig. 1(D)]. Each projection was acquired by selecting a random subphase from 1 to 100 representing the complete cardiac cycle and then by averaging the closest ten subphases, representing a 10 ms projection integration time and a heart rate of 600 beats/min. The MOBY phantom simulation experiment did not include respiratory motion. Prior to reconstruction, a realistic level of Poisson noise was added to the projection data (expected noise standard deviation: ∼80 HU in water). Using the previously described temporal basis functions to weight projections, the objective was to reconstruct ten phases of the cardiac cycle at two energies.
2.J. In vivo data
All in vivo data sets were acquired with our dual source microCT system,38 which consists of two identical imaging chains offset by 90°. Each chain consists of an Epsilon high frequency x-ray generator (EMD Technologies, Saint-Eustache, QC), a G297 x-ray tube (Varian Medical Systems, Palo Alto, CA; fs = 0.3/0.8 mm; tungsten rotating anode; filtration: 0.7 mm Al and 3 mm PMMA), and a XDI-VHR CCD x-ray detector (Photonic Science Limited, Robertsbridge, UK; 22 μm pixels) with a Gd2O2S scintillator. All in vivo experiments were approved by the Institutional Animal Care and Use Committee at Duke University.
The prospectively gated Tie2Cre; p53FL/− mouse data set [end diastole, Fig. 3(A)] was acquired with cardiorespiratory gating8 using 40 kVp, 250 mA, and 16 ms per exposure for one x-ray source and 80 kVp, 160 mA, and 10 ms for the second x-ray source. In previous work, these sampling kVps were found to be optimal for separating iodine and gold contrast.40 The free-breathing animal was scanned while under anesthesia induced with 1% isoflurane delivered by nose cone. Both x-ray tubes were triggered simultaneously at the coincidence of end diastole and end-expiration. The ECG signal was recorded with BlueSensor electrodes (Ambu A/S, Ballerup, DK) taped to the front footpads. Body temperature was maintained at 38 °C with heat lamps connected to a rectal probe and a Digi-Sense feedback controller (Cole-Parmer, Vernon Hills, IL). A pneumatic pillow on the thorax was used to monitor respiration. Three hundred equiangular projections (1002 × 667, 88 μm pixels) were acquired per x-ray source/detector. The dual source scan required about 5 min to complete. Reconstruction was performed using the Feldkamp algorithm41 and resulted in reconstructed 40 and 80 kVp volumes with isotropic 88 μm voxels. The estimated radiation dose was 130 mGy.
The same mouse [Fig. 3(B)] and a second Tie2Cre; p53FL/+ mouse were used to acquire 5D data sets to test the proposed algorithm. The 5D data sets were acquired with retrospective cardiac gating.42 Projection images were acquired at 80 kVp, 100 mA, 10 ms per exposure and 40 kVp, 200 mA, 10 ms per exposure without waiting for cardiac and respiratory coincidence. Respiratory and ECG signals were recorded in synchrony with the acquisition of the projections. During the acquisitions, the mice were free breathing (p53FL/− mouse: 46 breaths/min, 425 heart beats/min; p53FL/+ mouse: 44 breaths/min, 415 heart beats/min). Sampling involved a single rotation of the animal (360 ˚), resulting in 225 projections per imaging chain (per energy). A total of 450 projections (1002 × 667, 88 μm pixels) were acquired with an acquisition time of less than 1 min per animal. The final angular pitch, including the projections from both energies, was 0.8°. 5D reconstruction resulted in 20 3D volumes corresponding to ten phases of the cardiac cycle sampled at two energies. The reconstructed matrix size was 768 × 768 × 250 with isotropic 88 μm voxels. The estimated radiation dose was 60 mGy.
Prior to reconstruction, the distribution of sampled cardiac phases was confirmed to be approximately uniform, with minimal correlation between projection angle and cardiac phase. As previously discussed in Sec. 2.C, respiratory gating was enforced retrospectively by excluding (i.e., assigning a zero weight to) projections acquired during respiratory phases 8 and 9 of 10 total respiratory phases. As expected, this reduced the number of projections used for reconstruction by ∼20% (225 projections/energy to ∼180 projections/energy). The relationship between this respiratory gating strategy and the rank-sparse signal model (Fig. 1) is analyzed in Sec. 4.
Following 5D reconstruction of the Tie2Cre; p53FL/− and Tie2Cre; p53FL/+ data sets, automated segmentation of the left ventricle was performed using methods outlined in previous work,43 including label smoothing with Atropos.44 We note that Atropos exploited the spectral contrast, using both sampled energies in the label smoothing process. The spectral contrast facilitated the separation of iodine in the blood pool from gold at the site of myocardial injury in the Tie2Cre; p53FL/− mouse data set. Following label smoothing, the left ventricle label was used to measure end diastolic volume (EDV), end systolic volume (ESV), stroke volume (SV = EDV − ESV), ejection fraction (100 * SV/EDV), and cardiac output (heart rate * SV).
3. RESULTS
3.A. Simulations
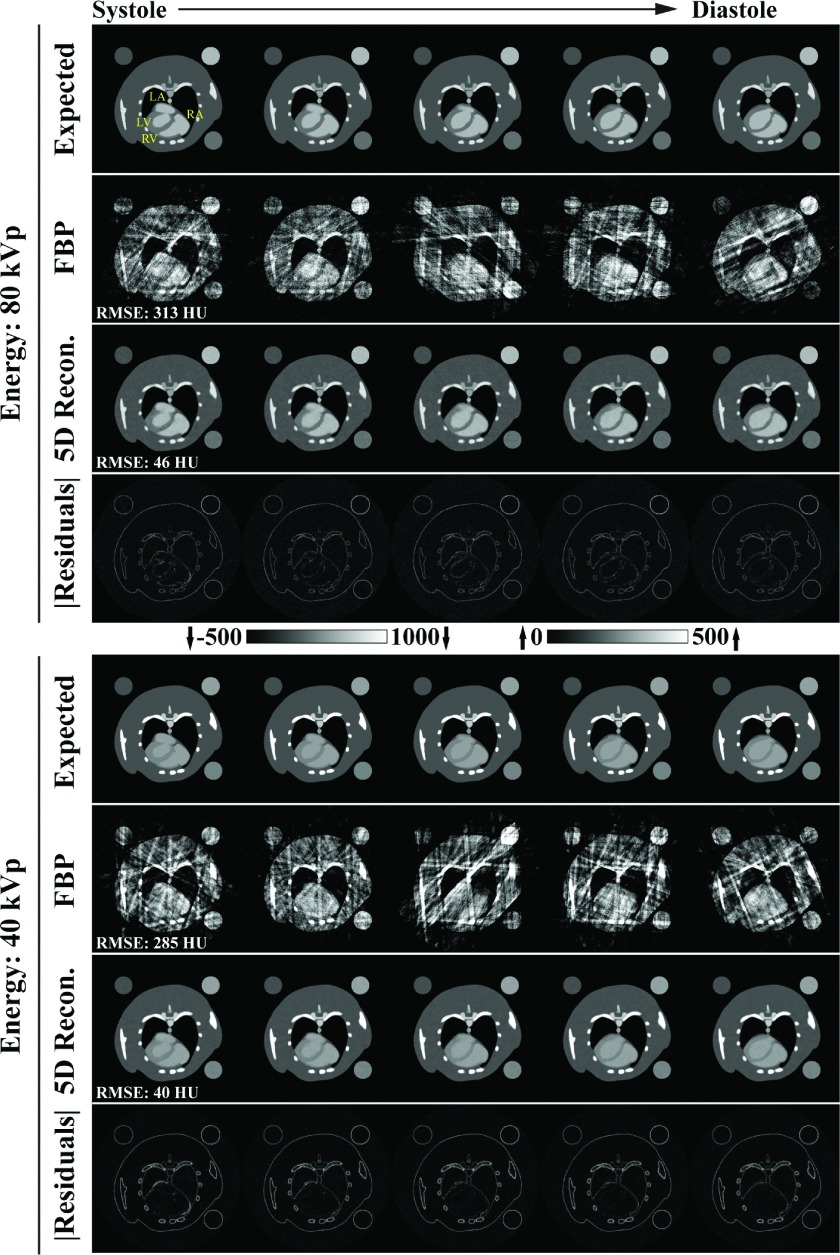
Figure 4 summarizes the results of the 5D MOBY phantom simulation experiment, comparing the expected reconstruction results with temporally weighted filtered backprojection reconstructions (Sec. 2.C) and the results obtained with the proposed 5D reconstruction algorithm (Fig. 2). 5D reconstruction with RSKR provides a 7-fold reduction in root-mean-square error (RMSE, averaged over all phases) over the FBP reconstructions for both energies. As a point of reference, the RMSE values for 5D reconstruction (80 kVp: 46 HU; 40 kVp: 40 HU) are well below even the expected error due to noise in a regularly sampled FBP reconstruction (RMSE = expected noise standard deviation: ∼80 HU). Furthermore, the absolute residual images, which compare the 5D reconstruction results with the expected reconstruction results, show highly accurate recovery of the atria and ventricles at each cardiac phase shown (systole through diastole). This observation is quantitatively verified in Fig. 5 which compares matching line profiles taken through the left atrium, myocardium, left ventricle, and the liver for the 80 kVp data in the coronal orientation. Comparing weighted FBP reconstruction results with the 5D reconstruction results, the RMSE associated with the dynamic line profile is reduced from 320 to 53 HU at ventricular systole and from 286 to 41 HU at ventricular diastole.
FIG. 4.
Summary of results from the 5D MOBY mouse phantom simulation experiment. A spatially matching 2D slice is shown in each panel. (Columns) First 5 of 10 cardiac phases spanning ventricular systole through diastole (yellow labels: LA, left atrium; RA, right atrium; LV, left ventricle; RV, right ventricle). (Rows) “Expected” reconstruction results including the 10 ms integration time, weighted “FBP” reconstruction results, 5D reconstruction (“5D Recon.”) results using the proposed algorithm (Fig. 2), and absolute residuals (“|Residuals|”) for the 5D reconstruction results. The CT data are scaled in HU as shown. Note that, as shown, the residuals are amplified by a factor of three relative to the grayscale data. RMSE: Root-mean-square error metric averaged over all ten phases.
FIG. 5.
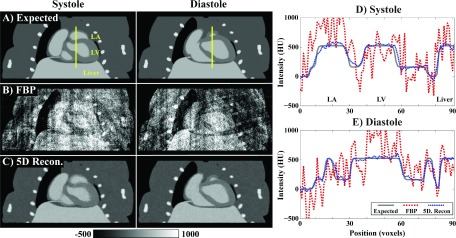
Recovery of spatiotemporal resolution in the 5D MOBY mouse phantom simulation experiment. (A) Spatially matching, coronal, 2D slices through the expected reconstruction results for ventricular diastole and systole at 80 kVp. The expected reconstructions are averaged over the 10 ms projection integration time. Yellow vertical lines denote spatially matching line profiles plotted in (D) and (E). The line profiles extend through the left atrium (LA) and left ventricle (LV) and then through the liver. (B) Corresponding temporally weighted FBP reconstruction results. (C) Corresponding 5D reconstruction results (Fig. 2). CT data are scaled in HU as denoted by the calibration bar (bottom, left). (D) Line profile from (A) plotted for each reconstruction result at ventricular systole. Line profile RMSE: FBP, 320 HU; 5D Recon., 53 HU. (E) Line profile from (A) plotted for each reconstruction result at ventricular diastole. Line profile RMSE: FBP, 286 HU; 5D Recon., 41 HU.
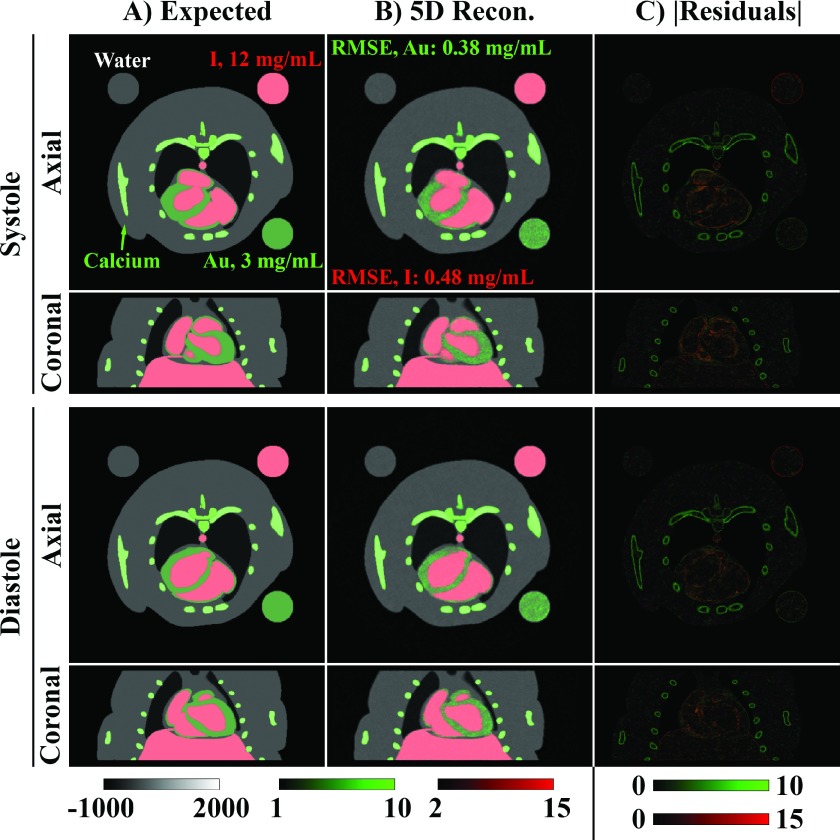
Figure 6 compares the expected material decomposition (A) with the material decomposition results following 5D reconstruction (B) overlaid on the reconstructed 80 kVp data. Given realistic concentrations of iodine (I, 12 mg/ml) in the blood pool and gold (Au, 3 mg/ml) in the myocardium, the temporal resolution and the accuracy of the material decomposition are seen to be high enough to differentiate the two materials in both the axial and coronal orientations. Specifically, the RMSE of the material decomposition is seen to be 13% of the gold concentration in the myocardium (RMSE: 0.38 mg/ml) and 4% of the iodine concentration in blood pool (RMSE: 0.48 mg/ml). Absolute residual images for the CT data at each energy (Fig. 4) and, correspondingly, for the material decompositions [Fig. 6(C)] localize the largest errors to edge features which are slightly smoothed relative to the expected discretized phantom; however, the errors do not appear to be strongly correlated with the dynamic portion of the reconstruction, denoting accurate recovery of the temporal resolution.
FIG. 6.
5D MOBY phantom material decomposition results for matching 2D slices in coronal and axial orientations for ventricular systole and diastole. (A) Expected reconstruction results including the 10 ms integration time. For context, the iodine (I, red) and gold (Au, green) material maps are overlaid on the corresponding 80 kVp grayscale data. Calcium (bone) appears as gold in the decomposed images. (B) Corresponding 5D reconstruction results produced with the proposed algorithm (Fig. 2). (C) Gold and iodine absolute residual images. Iodine and gold concentrations are scaled as shown in mg/ml. RMSE: Root-mean-square error metric for the material decompositions averaged over all ten phases. CT data are scaled in Hounsfield units.
3.B. In vivo data
Figure 7 compares analytical reconstruction results using weighted FBP with corresponding reconstruction results produced by the proposed 5D algorithm for the p53FL/− mouse and the p53FL/+ mouse. The proposed algorithm not only removes a substantial amount of noise from the time average reconstructions at each energy (noise standard deviation: FBP, ∼130 HU; 5D Recon., ∼30 HU) but also does so in such a way that the joint image structure at each energy is emphasized, preconditioning the results for material decomposition. The static portions of the time-resolved reconstructions at each energy, which are regularized jointly with the time and energy averaged reconstruction, are seen to become highly redundant. Based on the prior expectation that the temporal contrast is spatially sparse, this is the expected outcome (Fig. 1). Within the heart, the nonzero temporal contrast is seen to clearly differentiate ventricular systole from ventricular diastole in the healthy p53FL/+ mouse.
FIG. 7.
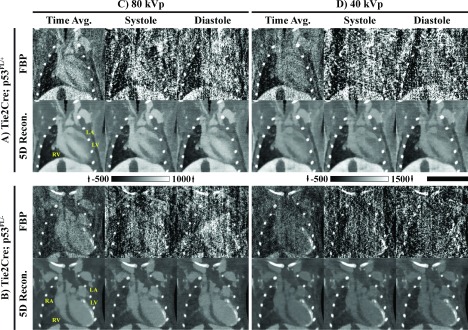
In vivo 5D reconstruction results. Rows: Reconstruction results for the (A) Tie2Cre; p53FL/+ mouse and for the (B) Tie2Cre; p53FL/− mouse. Results consist of matching weighted FBP reconstructions and 5D reconstructions using the proposed algorithm (Fig. 2). Columns: Reconstructions at (C) 80 kVp and (D) 40 kVp. Time-averaged reconstructions as well as reconstructions at end systole and end diastole are shown for matching 2D slices. Yellow, anatomic labels: RA, right atrium; LA, left atrium; RV, right ventricle; LV, left ventricle. CT data are scaled in Hounsfield units with a different scaling for (A) and (B) as shown. Scale bar: 1 cm.
Figure 8(A) (p53FL/+) and 10(A) (p53FL/−) expand the energy average temporal dimension, showing the reconstruction at each temporal phase, as well as the recovered spatially sparse temporal contrast images (i.e., columns of XS; Fig. 1). For the p53FL/+ animal, cardiac function of the left and right ventricles (LV and RV) and the left atrium (LA) appears normal, with clear differences in volume between ventricular diastole and systole. This observation is verified by the line profiles plotted in Fig. 9 which highlight the differences between ventricular diastole and systole in the left atrium and left ventricle. Furthermore, the reconstruction of the liver is seen to remain consistent in time. By contrast, contraction of the LV is clearly compromised in the p53FL/− animal, consistent with the reduction in left ventricle ejection fraction and stroke volume previously observed in five p53FL/− animals (relative to five p53FL/+ animals) 8 weeks after partial heart irradiation.26 For the results in this paper, these observations are supported by the left ventricle functional metrics summarized in Table I and derived by automated segmentation of the 5D reconstruction results. Expanding ventricular diastole along the energy dimension [yellow boxes, Figs. 8(B) and 10(B)] allows material decomposition into iodine (red) and gold (green) maps. In the p53FL/− animal, which is susceptible to the development of perfusion defects,26 a high concentration of gold is seen to have accumulated at the site of myocardial irradiation [yellow arrows, Fig. 10(B)], positively identifying and outlining a myocardial perfusion defect.
FIG. 8.
In vivo 5D reconstruction results for the Tie2Cre; p53FL/+ mouse (Ref. 45). (A) Energy averaged reconstruction results at each of ten cardiac phases, including difference images between each phase and the time-averaged reconstruction. Anatomic labels (upper, left): LA, left atrium; RV, right ventricle; LV, left ventricle. (B) End diastole at 80 and 40 kVp followed by postreconstruction material decomposition results (red, iodine; green, gold). CT data and difference images are scaled in Hounsfield units as shown. Iodine and gold concentrations are scaled as shown in mg/ml. Scale bars: 1 cm.
FIG. 10.
In vivo 5D reconstruction results for the Tie2Cre; p53FL/− mouse (Ref. 45). (A) Energy average reconstruction results at each of ten cardiac phases, including difference images between each phase and the time-averaged reconstruction. Anatomic labels (upper, left): RA, right atrium; LA, left atrium; RV, right ventricle; LV, left ventricle. (B) End diastole at 80 and 40 kVp followed by postreconstruction material decomposition results (red, iodine; green, gold). Arrows denote the center of a perfusion defect caused by partial heart irradiation. CT data and difference images are scaled in Hounsfield units as shown. Iodine and gold concentrations are scaled as shown in mg/ml. Scale bars: 1 cm.
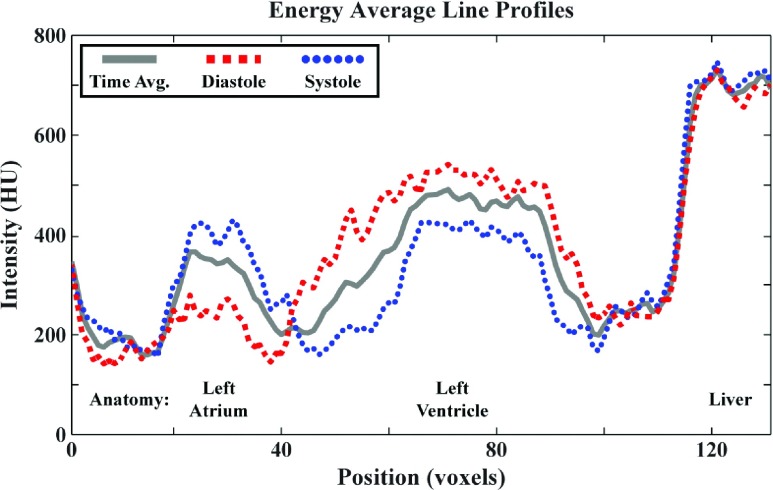
FIG. 9.
Spatially matching line profiles generated from the energy average, in vivo 5D reconstruction results for the Tie2Cre; p53FL/+ mouse [Fig. 8(A)]. The line profile is illustrated in yellow on the systole panel of Fig. 8(A). Here, the line profile is plotted for the energy average reconstruction at diastole and systole as well as for a corresponding line profile in the time and energy average (“Time Avg.”) reconstructions (solid gray). Peaks corresponding to the spatial positions of the left atrium, left ventricle, and the liver are marked at the bottom of the plot.
TABLE I.
Cardiac functional metrics (left ventricle).
| Genotype | End diastolic volume (μl) | End systolic volume (μl) | Stroke volume (μl) | Ejection fraction (%) | Respiratory rate (breaths/min) | Heart rate (beats/min) | Cardiac output (ml/min) |
|---|---|---|---|---|---|---|---|
| Tie2Cre; p53FL/+ | 49.15 | 18.28 | 30.87 | 62.81 | 44 | 415 | 12.81 |
| Tie2Cre; p53FL/− | 103.46 | 85.89 | 17.57 | 16.89 | 46 | 425 | 7.47 |
Referring back to Fig. 3(B), we see that these retrospective reconstruction results for end diastole in the p53FL/− mouse compare favorably with prospectively gated reconstruction results acquired for the same phase and in the same animal. Comparing the “prospective” imaging protocol with the “low-dose retrospective” protocol (Table II) used to produce the results in Fig. 3(B), we see a 92.5% reduction in the amount of projection data acquired per cardiac phase and energy, a 95% reduction in radiation dose per cardiac phase and energy, and a 40-fold decrease in the projection sampling time. As mentioned in Sec. 1, due to the excessive dose associated with the prospective imaging protocol, only a single phase was acquired at two energies using this protocol (dose: ∼130 mGy); even so, the results in this paper represent a 25% reduction in the total number of projections used (600 vs 450) to reconstruct 10 times the amount of data. As a point of reference, Table II also includes the “retrospective” imaging protocol used to measure cardiac functional metrics in previous work26 where it was referred to as “4D-microCT.”
TABLE II.
CT imaging protocols.
| Projection gating | Cardiac phases | Energies | Projection No. | Sampling time (min) | mAs/projection (80, 40 kVp) | Approximate dose (mGy) |
|---|---|---|---|---|---|---|
| Prospective | 10 | Dual | 6000 | 40 | 1.6, 4 | 1300 |
| Retrospective | 10 | Single | 2250 | 5 | 1, 2 | 290 |
| Low dose retrospective | 10 | Dual | 450 | <1 | 1, 2 | 60 |
3.C. Computational considerations
As previously discussed in Sec. 2.J, the in vivo reconstruction results presented in this paper (Figs. 3, 7, 8, and 10) consist of 20 768 × 768 × 250 volumes reconstructed with 88 μm isotropic voxels (10 phases × 2 energies = 20 volumes) from 450 projections acquired across two imaging chains. All computations were performed on a stand-alone workstation with a 6-core Intel Core i7 processor clocked at 4.0 GHz, 64 GB of system RAM, and a GeForce GTX 780 graphics card with 3 GB of dedicated onboard RAM. Iterative reconstruction was performed using GPU-based implementations of voxel-driven backprojection and ray-driven reprojection.42 All BF operations were also performed on the GPU. All GPU codes were compiled and executed using NVIDIA’s CUDA libraries (toolkit: v6.0, compute capability: 3.5). All geometric calculations were performed in double precision. All other computations were performed in single precision. The total computation time to execute three iterations of the proposed algorithm, including least squares initialization (Fig. 2, step 1), was ∼5.5 h [16.5 min/phase/energy], with no perceptible changes in image quality resulting from additional iterations. All simulations and in vivo results in this work are converged and are shown after three iterations of the proposed algorithm.
4. DISCUSSION AND CONCLUSIONS
In Sec. 1, we raised the question of whether or not 5D reconstruction from a limited (and perhaps even predetermined) amount of projection data can be a tractable inverse problem. As outlined in Fig. 1, we have set up the reconstruction problem as follows. Globally, we acquire our projection data with regular angular sampling suitable for high-fidelity reconstruction with an analytical method (i.e., filtered backprojection). For the spectral dimension, this global projection distribution is subdivided into two (or more) angularly interleaved subsets of projections. For the temporal dimension, we assume that the temporal sampling is uncorrelated with projection angle and approximately uniform across the cardiac cycle. We also assume that any dynamic motion is cyclic (e.g., cardiac cycle and respiratory cycle) such that it sums to zero over time. Intuitively, if these conditions are met, the spectral and temporal reconstruction problems are approximately independent [Eq. (25)]. For the spectral reconstruction problem, we are attempting to recover dense, but gradient sparse, spectral contrast with a dimensionality equal to one less than the number of energies we are attempting to reconstruct [Eq. (21)]. For the temporal reconstruction problem, we must recover a larger number of temporal contrast images, but each image is more heavily constrained to be spatially sparse and to be consistent with its neighbors [Eq. (23)]. In both cases, we are enforcing gradient sparsity relative to the same high-fidelity template through RSKR, meaning that the spectral contrast and the temporal contrast images we recover exhibit coherent image structure. In summary, if these assumptions hold, we can share projections between the temporal and spectral dimensions, enabling us to solve the 5D reconstruction problem from highly undersampled data.
The results presented in this work address the most common spectral sampling case, dual energy CT data acquired with energy integrating detectors; however, the proposed 5D CT reconstruction algorithm (Fig. 2) extends to an arbitrary number of spectral samples. Specifically, the data-fidelity update steps (Fig. 2, steps 1 and 8) apply to each time point and energy independently [Eqs. (1) and (4)], and, therefore, innately handle an arbitrary number of spectral samples. Regarding spectral regularization (Fig. 2, step 3), the decomposition of the spectral dimension into the time and energy average image, , and the spectral contrast, XEnergy, is equivalent to principal component decomposition, where XEnergy has NE − 1 independent columns (Sec. 2.E). Joint BF is then applied between and the columns of XEnergy. We have previously demonstrated effective joint BF of multiple spectral samples using 3 kVps sampled with an energy integrating detector18 and using full-spectrum CT data acquired with a photon counting x-ray detector.19 The only caveat in applying the proposed algorithm to generic spectral reconstruction problems is that the proposed separable approximation [Fig. 1; Eqs. (19) and (25)] will break down when the magnitude of the spectrotemporal contrast, rt,e, becomes significant relative to the magnitude of the temporal contrast, XTime. This will happen, for instance, when performing K-edge imaging of a dynamic feature using a photon counting x-ray detector. Nominally, this 5D reconstruction problem can be handled by performing explicit 5D BF, extending the spectral filtration operation along the temporal dimension; however, this approach sacrifices the approximate independence of the time and energy dimensions. In future work, we will attempt to extend our separable approximation to handle arbitrary spectral sampling cases by further exploiting the redundancy in image structure which persists regardless of differences in contrast.
For applications where the number of spectral samples is small (e.g., dual energy) and the separable approximation holds, the temporal reconstruction problem will determine the amount of projection data needed for accurate reconstruction. Given any reasonable number of projections, we expect to make progress with the temporal reconstruction problem because of the broad base of support of the temporal basis functions and the availability of a high-fidelity temporal average image. For highly undersampled cases [here, 22.5 projections/energy/phase] where the initialization inadequately recovers the temporal resolution (Fig. 2, step 1), a balance must be struck between enforcing regularity relative to the temporal average and recovering temporal resolution during the data-fidelity update step (Fig. 2, step 8). Over regularizing causes underestimation of the temporal resolution, while under regularizing leaves noise and shading artifacts in the reconstructed result. In future work, we will investigate this relationship more thoroughly by quantifying the tradeoff between projection number and recovered temporal resolution. Potential metrics for this purpose include temporal modulation transfer measurements and the reproducibility of derived cardiac functional metrics. We will also investigate methods to decorrelate the projection angular sampling from specific cardiac phases to avoid inconsistent reconstruction results between phases.
Further regarding the temporal reconstruction problem and given the application of partial heart irradiation, we have focused on the recovery of cardiac motion. For the MOBY phantom experiments presented in this work, no respiratory motion was modeled. For the in vivo experiments, respiratory motion was recorded using a pneumatic pillow. The recorded respiratory signal was then used retrospectively to assign zero weights to projections recorded during respiratory phases 8 and 9 (of ten phases of equal length starting and ending at end inspiration). These phases were determined to be outliers by looking at the reprojection residuals following initialization of the algorithm (Fig. 2, step 1) without respiratory gating, and then by correlating the largest residuals with respiratory phase. Consistent with previous work,46 gating for respiratory phase had little impact on the recovered cardiac motion; however, the absence of respiratory gating did result in shading artifacts near the diaphragm and liver which were inconsistent between the reconstructed cardiac phases. Given that the primary objective of this work was to derive an algorithm that provides reliable results from randomly sampled projection data, we chose to assign zero weights to projections acquired during respiratory phases 8 and 9. Based on the temporal contrast images shown in Figs. 8 and 10 and the line profiles in Fig. 9, this approach worked well for the two in vivo data sets presented in this work. Strictly speaking, however, removing projections diverges from the hierarchical sampling strategy outlined in Fig. 1, since projections are indirectly removed from the well-sampled time and energy averaged data. In future work, we propose to investigate the use of nonzero respiratory weights, perhaps assigned based on the reprojection residuals following unweighted initialization, to strike a balance between consistent reconstruction results and ideal projection sampling.
Assuming we can reliably undersample the projection data to control radiation dose and imaging time without sacrificing reconstructed image quality, the required computation time for 5D reconstruction could still be a significant issue. For the in vivo results presented here, the projection acquisition time was <1 min vs ∼5.5 h for reconstruction [16.5 min/phase/energy]. Thanks to a GPU-based implementation and the separability of the temporal and spectral problems, regularization with BF (RSKR) is quite efficient (∼10 min/iteration). In other words, the data-fidelity update steps dominated the total computation time (Fig. 2, steps 1 and 8). The use of broad temporal basis functions notably increases the computation time when every projection has a nonzero contribution to the reconstruction of each temporal phase. In future work, it may be possible to reduce the computation time by truncating the temporal basis functions and relaxing the constraint that the temporal basis functions exactly sum to a uniform distribution. More interesting, however, is the promise of parallelizing the GPU code across multiple GPUs. The split Bregman method inherently subdivides the reconstruction problem into highly parallelizable subproblems. Since all of the BF steps and then all of the data-fidelity update steps can be run in parallel, the algorithm could scale almost linearly with the available number of GPUs. We look to take advantage of parallelization across multiple GPUs in future work.
In conclusion, we have outlined and demonstrated a complete algorithm for 5D CT reconstruction from retrospectively gated projection data. By following fairly general guidelines for the data acquisition, we have argued that the problem of 5D CT reconstruction from undersampled projection data is not only possible but also reasonably well conditioned when the low-rank nature of the spectral reconstruction problem and the sparse nature of the temporal reconstruction problem are exploited in tandem. In addition to preclinical applications of 5D CT like the one presented here, we believe our methods could find clinical application, particularly in intraoperative C-arm CT reconstruction from retrospectively gated projection data. In the more distant future, the continued development of photon counting x-ray detectors as a supplement, or even replacement, for traditional energy-integrating detectors will make 5D CT data acquisition and reconstruction routine, as dynamic data sets will inherently be supplemented with spectral information. We look forward to applying our methods to these and other 5D CT imaging applications.
ACKNOWLEDGMENTS
All the work was performed at the Duke Center for In Vivo Microscopy, a NIH/NIBIB National Biomedical Technology Resource Center (No. P41 EB015897). This research was supported by a grant from Susan G. Komen for the Cure® (No. IIR13263571) and by NIH funding through the National Cancer Institute (No. R01 CA196667). Additional support was provided by an American Heart Association predoctoral fellowship (No. 12PRE10290001). The authors have no conflicts of interest.
APPENDIX: SUPPLEMENTAL DERIVATIONS
1. Data fidelity weighting for temporal reconstruction
The temporally selective weights, T, [Eq. (8)] are redundant for all line integrals within a single projection. The weight for a given projection is determined by the time point to be reconstructed, t, and the time during the cardiac, R–R interval at which the projection was acquired, u,
| (A1) |
| (A2) |
| (A3) |
As shown in Eq. (A1), T consists of Gaussian temporal weights computed from the minimum cyclic distance in time between t and u [Eq. (A2)]. NU is the R–R interval in milliseconds (cardiac R–R interval of a mouse: ∼100 ms). NT is chosen to be ten phases. As a result [Eq. (A3)], the expected full width at half maximum of 10 ms matches the projection integration time (Secs. 2.I and 2.J). To assign equal a prior weight to all possible temporal samples (i.e., to make the basis functions sum to a uniform distribution in time), a small correction factor is applied to each temporal basis function, yielding corrected weights, T′,
| (A4) |
In other words, Eq. (A4) equalizes the mean of the Gaussian basis functions at every possible time, u. For each time point, these corrected weights are then normalized such that they sum to one. Given these weights, enforcing data fidelity for a given cardiac phase amounts to interpolating the reconstruction of that phase from among the acquired temporal samples.
2. The split Bregman method for rank-sparsity constrained CT reconstruction
The 5D reconstruction algorithm outlined in Sec. 2.G and Fig. 2 solves the following optimization problem [previously, Eq. (38)]:
| (A5) |
As in the text [Eq. (4)], the data fidelity term implies columnwise evaluation, including the time point and energy dependent weighting matrix, Q [Eq. (8)]. For brevity, we work with a single BTV regularization term as previously defined in Eq. (17); however, the derivation can be readily extended to include additional BTV terms with variable range weighting schemes [Eq. (37)]. Following the approach in the PRISM algorithm,16 the dummy variable, d, is introduced,
| (A6) |
Note that Eq. (A6) is equivalent to Eq. (A5) when X = d. Introducing this dummy variable ultimately allows the data fidelity term and the BTV term to be minimized in separate substeps. As in the split Bregman method29 and the alternating direction method of multipliers,47 the conditioning and convergence of Eqs. (A5) and (A6) is improved by constructing and evaluating the Lagrangian function, L, with Lagrange multipliers (residuals), f and v,
| (A7) |
The f multiplier (NY rows and NE ⋅ NT columns) is introduced to minimize the time and energy specific data fidelity residuals. The v multiplier (NX rows and NE ⋅ NT columns) and μ regularization parameter are introduced to minimize X − d and thus equate Eqs. (A5) and (A6). The notation is introduced to denote inner products computed between and summed over time points and energies,
| (A8) |
Updating each variable in the Lagrangian function in turn [Eq. (A7)] solves the original optimization problem [Eq. (A5)].48 Following the update steps in the algorithm pseudocode (Fig. 2) and the order of the variables in the definition of L [Eq. (A7)], the d variable is first updated, while the v, f, and X variables are held constant (Fig. 2, steps 3–5),
| (A9) |
where the n superscript denotes variables which are held constant and which has not yet been updated during the current iteration. This expression reduces to the following:
| (A10) |
which is equivalent to Eq. (16). Consistent with both the add-residual-back strategy29 and kernel regression,32 we apply BF to Xn + vn to yield dn+1. We note that several iterations of BF could be required to strictly minimize Eq. (A10); however, for the work presented here, a single iteration of BF per iteration of the split Bregman method proved adequate for the algorithm to converge in ∼3 iterations (Sec. 3.C). In Subsection 3 of the Appendix, we revisit Eq. (A10) and previous work which relates it to several popular denoising schemes.33
Next, the multiplier variable, v, is updated by gradient ascent (Fig. 2, step 6),47
| (A11) |
| (A12) |
| (A13) |
where δ1 is the product of the regularization parameter μ and a new rate constant. When δ is chosen to equal 1 (as in Fig. 2), the dual definition of v as a Lagrange multiplier variable and a residual in the add-residual-back strategy is clear, since vn+1 is set equal to the residual computed between the input, Xn + vn, and output, dn+1, of the regularization operation [Eq. (A10)]. A similar update is applied to f,
| (A14) |
Again, δ2 is chosen to equal 1 (Fig. 2, step 7).
The last step of each Bregman iteration updates the estimate of the reconstructed image, X, at each time point and energy (Fig. 2, step 8),
| (A15) |
| (A16) |
where L in Eq. (A15) evaluates and reduces to the expression in Eq. (A16). Taking the derivative of Eq. (A16) and setting it equal to zero yields the following:
| (A17) |
which we solve for X using the biconjugate gradient stabilized method36 to yield Xn+1. We note that Eq. (A17) suggests appropriate values for the user-specified regularization parameter, μ. Specifically, effective values of μ are a small fraction (here, ∼2%) of for each time point and energy. As shown in Fig. 2, the four update steps [Eqs. (A10), (A13), (A14), and (A16)] are iterated until convergence.
3. Bilateral total variation
As defined in this work, several applications of the bilateral filter to Xn + vn minimizes the following cost function:
| (A18) |
This equation is derived in previous work from a general expression for a single iteration of weighted least squares solved with the Jacobi method.33 Here, we adapt the notation and assume that X, v, and d have a single column for simplicity,
| (A19) |
E(l, m) represents the weight assigned to the squared intensity difference between d(l) and d(l − m) computed within the valid domain of the offsets, m, and at all spatial positions, l. Depending on the domain size and the choice of weights, Eq. (A19) describes the first iteration of several popular denoising algorithms (weighted least squares, anisotropic diffusion, and robust estimation).33 When the weights are chosen to be
| (A20) |
Equation (A19) reduces to the following:
| (A21) |
The second term of Eq. (A21) is equivalent to our definition of BTV [Eq. (17)] for a single column, aside from the absence of our resampling kernel in the gradient computation [Eq. (14) vs Eq. (15)]. We note that the computation of BTV with a resampling kernel can cause the denominator of BTV (BF) to approach zero, resulting in numerical instability. In practice, this is not an issue since RSKR is applied once per iteration of the split Bregman method, immediately after the noise residuals (v) are added back in. In general, however, instability can be addressed by introducing a constant additive term into the denominator as in the Jacobi method.33 We call our approach BTV after previously published work which used a similar weighted intensity gradient penalty.34
REFERENCES
- 1.Bhavane R., Badea C., Ghaghada K. B., Clark D., Vela D., Moturu A., Annapragada A., Johnson G. A., and Willerson J. T., “Dual-energy computed tomography imaging of atherosclerotic plaques in a mouse model using a liposomal-iodine nanoparticle contrast agent,” Circ.: Cardiovasc. Imaging 6, 285–294 (2013). 10.1161/CIRCIMAGING.112.000119 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Badea C. T., Guo X., Clark D., Johnston S. M., Marshall C. D., and Piantadosi C. A., “Dual-energy micro-CT of the rodent lung,” Am. J. Physiol.: Lung Cell. Mol. Physiol. 302, L1088–L1097 (2012). 10.1152/ajplung.00359.2011 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Ashton J. R., Befera N., Clark D., Qi Y., Mao L., Rockman H. A., Johnson G. A., and Badea C. T., “Anatomical and functional imaging of myocardial infarction in mice using micro-CT and eXIA 160 contrast agent,” Contrast Media Mol. Imaging 9, 161–168 (2014). 10.1002/cmmi.1557 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Ashton J. R., Clark D. P., Moding E. J., Ghaghada K., Kirsch D. G., West J. L., and Badea C. T., “Dual-energy micro-CT functional imaging of primary lung cancer in mice using gold and iodine nanoparticle contrast agents: A validation study,” PLoS One 9, e88129 (2014). 10.1371/journal.pone.0088129 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Moding E. J., Clark D. P., Qi Y., Li Y., Ma Y., Ghaghada K., Johnson G. A., Kirsch D. G., and Badea C. T., “Dual-energy micro-computed tomography imaging of radiation-induced vascular changes in primary mouse sarcomas,” Int. J. Radiat. Oncol., Biol., Phys. 85, 1353–1359 (2013). 10.1016/j.ijrobp.2012.09.027 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Clark D. P., Ghaghada K., Moding E. J., Kirsch D. G., and Badea C. T., “In vivo characterization of tumor vasculature using iodine and gold nanoparticles and dual energy micro-CT,” Phys. Med. Biol. 58, 1683–1704 (2013). 10.1088/0031-9155/58/6/1683 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Badea C. T., Hedlund L. W., Cook J., Berridge B. R., and Johnson G. A., “Micro-CT imaging assessment of dobutamine-induced cardiac stress in rats,” J. Pharmacol. Toxicol. Methods 63, 24–29 (2011). 10.1016/j.vascn.2010.04.002 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Badea C. T., Hedlund L. W., and Johnson G. A., “Micro-CT with respiratory and cardiac gating,” Med. Phys. 31, 3324–3329 (2004). 10.1118/1.1812604 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Badea C. T., Johnston S. M., Qi Y., and Johnson G. A., “4D micro-CT for cardiac and perfusion applications with view under sampling,” Phys. Med. Biol. 56, 3351–3369 (2011). 10.1088/0031-9155/56/11/011 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Badea C. T., Schreibmann E., and Fox T., “A registration-based approach for cardiac micro-CT using combined prospective and retrospective gating,” Med. Phys. 35, 1170–1179 (2008). 10.1118/1.2868778 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Armitage S. E. J., Pollmann S. I., Detombe S. A., and Drangova M., “Least-error projection sorting to optimize retrospectively gated cardiac micro-CT of free-breathing mice,” Med. Phys. 39, 1452–1461 (2012). 10.1118/1.3681949 [DOI] [PubMed] [Google Scholar]
- 12.Bartling S. H., Stiller W., Grasruck M., Schmidt B., Peschke P., Semmler W., and Kiessling F., “Retrospective motion gating in small animal CT of mice and rats,” Invest. Radiol. 42, 704–714 (2007). 10.1097/RLI.0b013e318070dcad [DOI] [PubMed] [Google Scholar]
- 13.Ritschl L., Sawall S., Knaup M., Hess A., and Kachelrieß M., “Iterative 4D cardiac micro-CT image reconstruction using an adaptive spatio-temporal sparsity prior,” Phys. Med. Biol. 57, 1517–1525 (2012). 10.1088/0031-9155/57/6/1517 [DOI] [PubMed] [Google Scholar]
- 14.Chen G. H., Tang J., and Leng S., “Prior image constrained compressed sensing (PICCS): A method to accurately reconstruct dynamic CT images from highly undersampled projection data sets,” Med. Phys. 35, 660–663 (2008). 10.1118/1.2836423 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Candès E. J., Li X., Ma Y., and Wright J., “Robust principal component analysis?,” J. ACM 58, 1–37 (2011). 10.1145/1970392.1970395 [DOI] [Google Scholar]
- 16.Gao H., Yu H., Osher S., and Wang G., “Multi-energy CT based on a prior rank, intensity and sparsity model (PRISM),” Inverse Probl. 27, 115012 (2011). 10.1088/0266-5611/27/11/115012 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Gao H., Cai J.-F., Shen Z., and Zhao H., “Robust principal component analysis-based four-dimensional computed tomography,” Phys. Med. Biol. 56, 3181–3198 (2011). 10.1088/0031-9155/56/11/002 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Clark D. P. and Badea C. T., “Spectral diffusion: An algorithm for robust material decomposition of spectral CT data,” Phys. Med. Biol. 59, 6445–6466 (2014). 10.1088/0031-9155/59/21/6445 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Clark D., Touch M., Barber W., and Badea C., “Simultaneous imaging of multiple contrast agents using full-spectrum micro-CT,” Proc. SPIE 9412, 941222 (2015). 10.1117/12.2081049 [DOI] [Google Scholar]
- 20.EBCTCG, “Favourable and unfavourable effects on long-term survival of radiotherapy for early breast cancer: An overview of the randomised trials,” Lancet 355, 1757–1770 (2000). 10.1016/S0140-6736(00)02263-7 [DOI] [PubMed] [Google Scholar]
- 21.Fisher B., Anderson S., Bryant J., Margolese R. G., Deutsch M., Fisher E. R., Jeong J. H., and Wolmark N., “Twenty-year follow-up of a randomized trial comparing total mastectomy, lumpectomy, and lumpectomy plus irradiation for the treatment of invasive breast cancer,” N. Engl. J. Med. 347, 1233–1241 (2002). 10.1056/NEJMoa022152 [DOI] [PubMed] [Google Scholar]
- 22.Darby S. C., McGale P., Taylor C. W., and Peto R., “Long-term mortality from heart disease and lung cancer after radiotherapy for early breast cancer: Prospective cohort study of about 300,000 women in US SEER cancer registries,” Lancet Oncol. 6, 557–565 (2005). 10.1016/S1470-2045(05)70251-5 [DOI] [PubMed] [Google Scholar]
- 23.Cuzick J. et al. , “Cause-specific mortality in long-term survivors of breast cancer who participated in trials of radiotherapy,” J. Clin. Oncol. 12, 447–453 (1994). [DOI] [PubMed] [Google Scholar]
- 24.EBCTCG, “Effects of radiotherapy and surgery in early breast cancer. An overview of the randomized trials,” N. Engl. J. Med. 333, 1444–1455 (1995). 10.1056/NEJM199511303332202 [DOI] [PubMed] [Google Scholar]
- 25.Darby S. C., Ewertz M., McGale P., Bennet A. M., Blom-Goldman U., Bronnum D., Correa C., Cutter D., Gagliardi G., Gigante B., Jensen M. B., Nisbet A., Peto R., Rahimi K., Taylor C., and Hall P., “Risk of ischemic heart disease in women after radiotherapy for breast cancer,” N. Engl. J. Med. 368, 987–998 (2013). 10.1056/NEJMoa1209825 [DOI] [PubMed] [Google Scholar]
- 26.Lee C.-L., Min H., Befera N., Clark D., Qi Y., Das S., Johnson G. A., Badea C. T., and Kirsch D. G., “Assessing cardiac injury in mice with dual energy-microCT, 4D-microCT, and microSPECT imaging after partial heart irradiation,” Int. J. Radiat. Oncol., Biol., Phys. 88, 686–693 (2014). 10.1016/j.ijrobp.2013.11.238 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Rudin L. I., Osher S., and Fatemi E., “Nonlinear total variation based noise removal algorithms,” Physica D 60, 259–268 (1992). 10.1016/0167-2789(92)90242-F [DOI] [Google Scholar]
- 28.Daubechies I., Han B., Ron A., and Shen Z., “Framelets: MRA-based constructions of wavelet frames,” Appl. Comput. Harmonic Anal. 14, 1–46 (2003). 10.1016/S1063-5203(02)00511-0 [DOI] [Google Scholar]
- 29.Goldstein T. and Osher S., “The split Bregman method for L1-regularized problems,” J. Imaging Sci. 2, 323–343 (2009). 10.1137/080725891 [DOI] [Google Scholar]
- 30.Wang J., Li T., Lu H., and Liang Z., “Penalized weighted least-squares approach to sinogram noise reduction and image reconstruction for low-dose x-ray computed tomography,” IEEE Trans. Med. Imaging 25, 1272–1283 (2006). 10.1109/tmi.2006.882141 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Tomasi C. and Manduchi R., “Bilateral filtering for gray and color images,” in Sixth International Conference on - Computer Vision, Sponsored by the IEEE Computer Society, Bombay, India Narosa, January 4-7, 1998 (Narosa Publishing House, New Delhi, Madras, Bombay, Calcutta, London, 1998), pp. 839–846. [Google Scholar]
- 32.Takeda H., Farsiu S., and Milanfar P., “Kernel regression for image processing and reconstruction,” IEEE Trans. Image Process. 16, 349–366 (2007). 10.1109/TIP.2006.888330 [DOI] [PubMed] [Google Scholar]
- 33.Elad M., “On the origin of the bilateral filter and ways to improve it,” IEEE Trans. Image Process. 11, 1141–1151 (2002). 10.1109/TIP.2002.801126 [DOI] [PubMed] [Google Scholar]
- 34.Farsiu S., Robinson M. D., Elad M., and Milanfar P., “Fast and robust multiframe super resolution,” IEEE Trans. Image Process. 13, 1327–1344 (2004). 10.1109/TIP.2004.834669 [DOI] [PubMed] [Google Scholar]
- 35.Sawall S., Bergner F., Lapp R., Mronz M., Karolczak M., Hess A., and Kachelriess M., “Low-dose cardio-respiratory phase-correlated cone-beam micro-CT of small animals,” Med. Phys. 38, 1416–1424 (2011). 10.1118/1.3551993 [DOI] [PubMed] [Google Scholar]
- 36.Van der Vorst H. A., “Bi-CGSTAB: A fast and smoothly converging variant of Bi-CG for the solution of nonsymmetric linear systems,” J. Sci. Stat. Comput. 13, 631–644 (1992). 10.1137/0913035 [DOI] [Google Scholar]
- 37.S. Mukundan, Jr., Ghaghada K. B., Badea C. T., Kao C. Y., Hedlund L. W., Provenzale J. M., Johnson G. A., Chen E., Bellamkonda R. V., and Annapragada A., “A liposomal nanoscale contrast agent for preclinical CT in mice,” Am. J. Roentgenol. 186, 300–307 (2006). 10.2214/AJR.05.0523 [DOI] [PubMed] [Google Scholar]
- 38.Badea C. T., Johnston S., Johnson B., Lin M., Hedlund L. W., and Johnson G. A., “A dual micro-CT system for small animal imaging,” Proc. SPIE 6913, 691342 (2008). 10.1117/12.772303 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Segars W. P., Tsui B. M. W., Frey E. C., Johnson G. A., and Berr S. S., “Development of a 4-D digital mouse phantom for molecular imaging research,” Mol. Imaging Biol. 6, 149–159 (2004). 10.1016/j.mibio.2004.03.002 [DOI] [PubMed] [Google Scholar]
- 40.Badea C., Johnston S., Qi Y., Ghaghada K., and Johnson G., “Dual-energy micro-CT imaging for differentiation of iodine-and gold-based nanoparticles,” Proc. SPIE 7961, 79611X (2011). 10.1117/12.878043 [DOI] [Google Scholar]
- 41.Feldkamp L. A., Davis L. C., and Kress J. W., “Practical cone-beam algorithm,” J. Opt. Soc. Am. A 1, 612–619 (1984). 10.1364/JOSAA.1.000612 [DOI] [Google Scholar]
- 42.Johnston S. M., Johnson G. A., and Badea C. T., “Temporal and spectral imaging with micro-CT,” Med. Phys. 39, 4943–4958 (2012). 10.1118/1.4736809 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Clark D., Badea A., Johnson G. A., and Badea C. T., “Constructing a 4D murine cardiac micro-CT atlas for automated segmentation and phenotyping applications,” Proc. SPIE 8669, 86691P (2013). 10.1117/12.2007043 [DOI] [Google Scholar]
- 44.Avants B. B., Tustison N. J., Wu J., Cook P. A., and Gee J. C., “An open source multivariate framework for n-tissue segmentation with evaluation on public data,” Neuroinformatics 9, 381–400 (2011). 10.1007/s12021-011-9109-y [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.See supplementary material at http://www.civm.duhs.duke.edu/5D_recon2015/ for animated 5D reconstruction results for the in vivo data sets (Figs. 8 and 10).
- 46.Guo X., Johnston S. M., Qi Y., Johnson G. A., and Badea C. T., “4D micro-CT using fast prospective gating,” Phys. Med. Biol. 57, 257–271 (2012). 10.1088/0031-9155/57/1/257 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Gabay D. and Mercier B., “A dual algorithm for the solution of nonlinear variational problems via finite element approximation,” Comput. Math. Appl. 2, 17–40 (1976). 10.1016/0898-1221(76)90003-1 [DOI] [Google Scholar]
- 48.Cai J.-F., Osher S., and Shen Z., “Split Bregman methods and frame based image restoration,” Multiscale Model. Simul. 8, 337–369 (2009). 10.1137/090753504 [DOI] [Google Scholar]