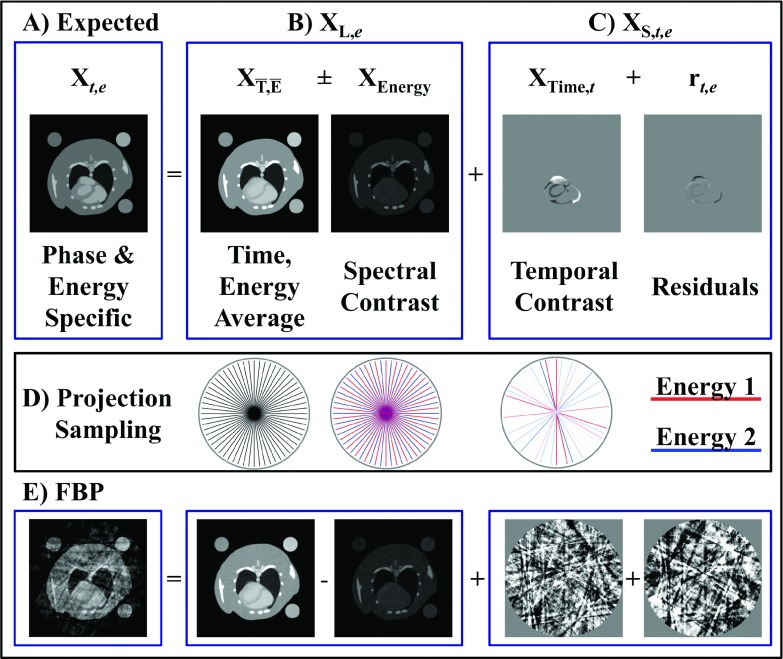
FIG. 1.
Rank-sparse signal model. (A) The expected reconstruction at a given time point and energy, Xt,e, is modeled as the sum of low-rank basis functions describing the energy dimension, XL,e, and sparse columns describing the spectrotemporal contrast, XS,t,e [Eq. (19)]. The independent columns of XL,e are chosen to correspond with the time and energy average reconstructions () and the spectral (“energy”) contrast (XEnergy). The sparse columns of XS represent the temporal contrast (XTime) and additional energy-dependent spectrotemporal contrast (rt,e). For dual energy CT using energy integrating detectors, the magnitude of rt,e is comparatively small, leading to a separable approximation by which the time and energy dimensions are regularized independently [Eq. (25)]. (D) The average reconstruction is regularly and densely sampled. The energy dimension is deterministically undersampled, while the time dimension is randomly sampled (projection intensity ∝ assigned weights). (E) Projection undersampling leads to noise and shading artifacts in FBP reconstructions; however, complementary image structure between each component can be exploited for high-fidelity regularization.