Significance
Gel electrophoresis is a ubiquitous biophysical technique. It consists of dragging charged biopolymers through a porous gel, by applying an electric field. Because the migration speed depends on topology, this method can be used to classify DNA knots. Currently, electrophoresis relies on empirical observations, and its theoretical understanding is limited. No theory can explain why knot mobility under strong fields depends nonmonotonically on complexity. Our study reveals a possible reason: Although complex knots have a smaller size, and hence move faster through the gel, they can become severely entangled with the gel, causing longer pauses. Our results can improve the design of future electrophoresis experiments.
Keywords: DNA knots, topology, gel electrophoresis
Abstract
Gel electrophoresis is a powerful experimental method to probe the topology of DNA and other biopolymers. Although there is a large body of experimental work that allows us to accurately separate different topoisomers of a molecule, a full theoretical understanding of these experiments has not yet been achieved. Here we show that the mobility of DNA knots depends crucially and subtly on the physical properties of the gel and, in particular, on the presence of dangling ends. The topological interactions between these and DNA molecules can be described in terms of an “entanglement number” and yield a nonmonotonic mobility at moderate fields. Consequently, in 2D electrophoresis, gel bands display a characteristic arc pattern; this turns into a straight line when the density of dangling ends vanishes. We also provide a novel framework to accurately predict the shape of such arcs as a function of molecule length and topological complexity, which may be used to inform future experiments.
Topology plays a key role in the biophysics of DNA and is intimately related to its functioning. For instance, transcription of a gene redistributes twist locally to create what is known as supercoiling, whereas catenanes or knots can prevent cell division; hence they need to be quickly and accurately removed by specialized enzymes known as topoisomerases. How can one establish experimentally the topological state of a given DNA molecule? By far the most successful and widely used technique to do so is gel electrophoresis (1, 2). This method exploits the empirical observation that the mobility of a charged DNA molecule under an electric field depends on its size, shape, and topology (2). Gel electrophoresis is so reliable that it can be used, for instance, to map replication origins and stalled replication forks (3), to separate plasmids with different amount of supercoiling (3, 4), and to identify DNA knots (5, 6). The most widely used variant of this technique nowadays is 2D gel electrophoresis, where a DNA molecule is subjected to a sequence of two fields, applied along orthogonal directions (2). The two runs are characterized by different field strengths and sometimes also gel concentrations (4); with suitable choices, the joint responses lead to increased sensitivity.
Although gel electrophoresis is used very often, and is extremely well characterized empirically, there is still no comprehensive theory to quantitatively understand, or predict, what results will be observed in a particular experiment. Some aspects are reasonably well established. For instance, it is now widely accepted that the physics of the size-dependent migration of linear polymers can be explained by the theory of biased polymer reptation (7–12). Likewise, the behavior of, for example, nicked, torsionally relaxed, DNA knots in a sparse gel and under a weak field is analogous to that of molecules sedimenting under gravity (13–15). The terminal velocity can be estimated via a balance between the applied force and the frictional opposing force, which is proportional to the average size of the molecule; as a result, more-complex knots, which are smaller, move faster under the field. However, the mechanisms regulating the electrophoretic mobility of DNA knots at intermediate fields, and in more-concentrated agar gels, are much less understood (4, 13, 16). Here, experiments suggest that the mobility of knots is usually a nonmonotonic function of the knot complexity, or, more precisely, of their average crossing number (5, 17) (ACN): Initially, knots move more slowly as their ACN increases, whereas, past a critical ACN, more-complex knots move faster. The combination of the responses to external fields directed along two perpendicular directions leads to a characteristic electrophoretic arc, which allows separation of the first simple knots more clearly in a 2D slab (4, 6, 18, 19). To our knowledge, there is currently no theoretical framework that quantitatively explains the nonmonotonic behavior at intermediate or large fields and the consequent formation of arc patterns.
To address this issue, here we present large-scale Brownian dynamics simulations of knotted DNA chains migrating through a gel, and subjected to a sequence of fields of different strength and direction, as in 2D gel electrophoresis experiments (see cartoon in Fig. 1A). We model the gel as an imperfect cubic mesh (20), where some of the bonds have been cut (see Materials and Methods) to simulate the presence of open strands, or dangling ends, which have been observed in physical agarose gels (21–27). Our results confirm the linear relation of the electrophoretic mobility with ACN for the first simple knots (we study ACN up to 12) in a sparse gel and under a weak field. However, our simulations also suggest that, due to a nonnegligible probability of forming “impalements” where a dangling end of the gel pierces a knot, the response of the chain to stronger fields is different. We suggest that, in this regime, the sole radius of gyration is not enough to explain the observed dynamics, and we introduce an average “entanglement number” that increases with the ACN and provides a measure of the likelihood of forming an impalement. The time needed by a knot to disentangle from the gel increases with its average entanglement number (AEN), or knot complexity, and this slows down the motion, thus competing with the Stokes friction, which leads to an increase of mobility with ACN. As a result of this contest, one typically gets a nonmonotonic behavior of the terminal speed with ACN, and an electrophoretic arc in two dimensions.
Fig. 1.
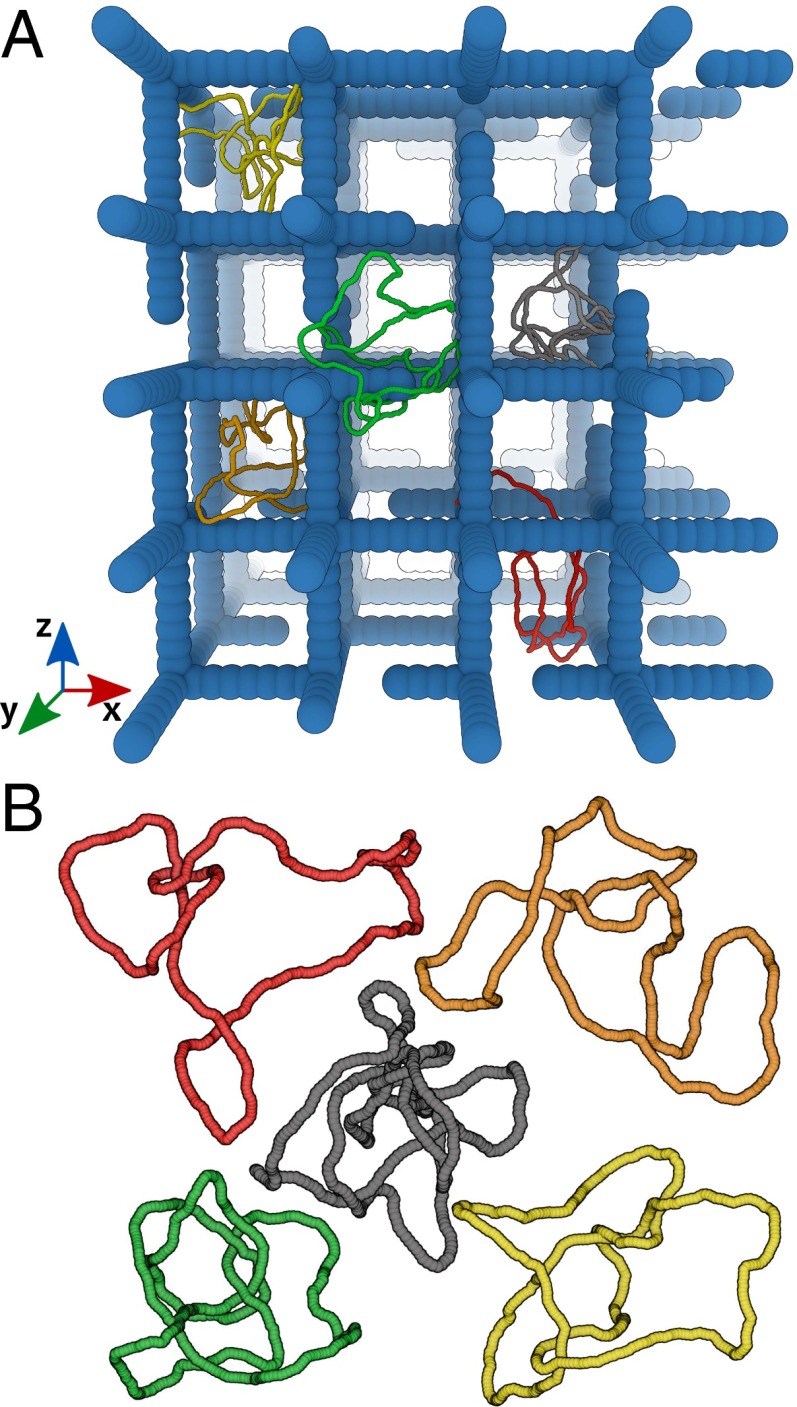
(A) Snapshot (to scale) of the model gel with some examples of knotted configurations. Note that, to model a physical gel, a simple cubic structure is randomly cut to create dangling ends. (B) Equilibrium configurations of some of the knots considered; it can be readily seen that the size tends to be smaller as the knot becomes more complex. The knots pictured in A and B are trefoil (), red; figure of eight (), orange; pentafoil (), yellow; Stevedore’s (), green; and nonafoil (), gray.
We also provide a simple model, based on a mapping between the DNA knot dynamics and a biased continuous-time random walk, which faithfully reproduces our Brownian dynamics simulations starting from a minimal number of assumptions. This approach can then be used to predict how the shape of the electrophoretic arc should depend on system parameters such as the average lattice spacing (pore size) of the gel and the contour length of DNA knots; as we shall see, the predicted trends are in agreement with existing 2D electrophoresis data. This constitutes, to our knowledge, the first example of a quantitative prediction of 2D electrophoretic diagrams; hence we suggest that the approach we present could potentially lead to even more accurate and targeted experiments to separate topoisomers in DNA or other polymers.
DNA Knots Form an Electrophoretic Arc only in Irregular Gels
The system we studied, sketched in Fig. 1 (see also Materials and Methods and Supporting Information), consists of 10 nicked, i.e., torsionally relaxed, DNA loops of kilobase pairs (kbp) within a model agarose gel with dangling ends. These loops are either unknotted or form one of the first few simple knots [with up to nine crossing in their minimal projection (28)]. The loops were first equilibrated within the gel (see Supporting Information) and then subjected to an in silico gel electrophoresis process where a weak electric field is first applied ( V/cm) along the vertical (z) direction, followed by a stronger field ( V/cm) along a transversal, say y, direction. We refer to these two fields as “weak” and “stronger,” or “moderate,” in what follows. The complete equations of motions and force fields used in our Brownian dynamics simulations are detailed in Supporting Information.
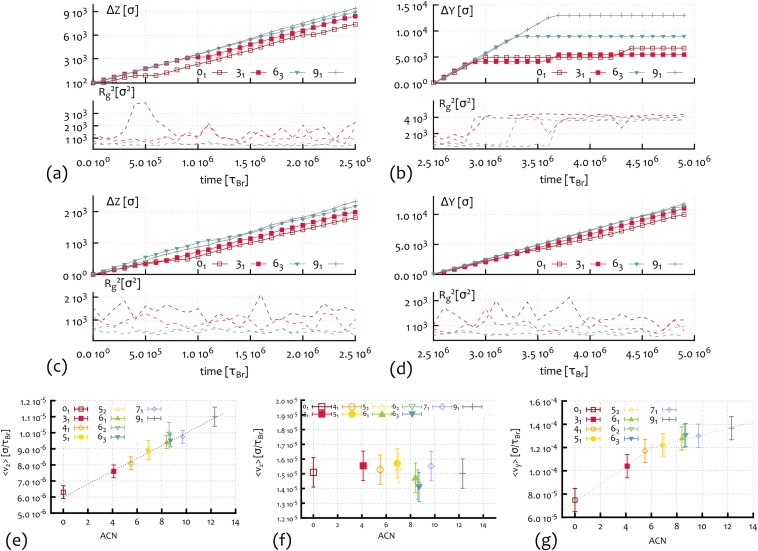
By monitoring the trajectories of the knots through the gel, we computed the average speed of their center of mass along each of the field directions (see Supporting Information and Fig. 2 A and B). As expected, the mobility along the direction of the weak field increases with the topological complexity of the configurations. Along the direction of the moderate field, however, the mobility of the knots displays a nonmonotonic behavior. In particular, the unknot now moves faster than either the trefoil or the twist knot, and has an average speed similar to the knot. This nonmonotonic behavior of the knot mobility, as a function of the ACN, was previously observed in typical experiments with torsionally relaxed DNA knots (4, 6, 18, 19, 29). It is worth noticing that, within the five-crossings family, the torus knot moves more slowly than the twist knots. This is similar to what was observed in the weak field case (although much less enhanced) but different from what is observed in experiments of sedimentation (15).
Fig. 2.
In silico 2D gel electrophoresis for knotted DNA loops. (A) Average velocity of different types of knotted polymers along the direction of the weak electric field: V/cm. The dotted line indicates the linear increase with the ACN. (B) Average velocity of different types of knotted polymers along the direction of the moderate field V/cm. (C) A 2D reconstruction of the spatial distribution of the knots as Gaussian probability distributions centered in [,], where and are the average speeds along, respectively, the weak and stronger field direction of knot type K, as found by Brownian dynamics simulations. The electrophoretic run times correspond to min and min. The spread of each spot has been estimated by looking at the SD of and . (Examples of single trajectories along the z and y directions are reported in Fig. S1). (D) Outcome of a 2D gel electrophoresis experiment performed on P4 viral DNA (10 kbp) at 0.4% agarose concentration [reprinted with permission from ref. 6 (Arsuaga et al.)].
To better compare our findings with experiments, we report, in Fig. 2C, the spatial distribution of the knots as Gaussians centered in [,] where and are the velocities along z (weak field direction) and y (stronger field direction) of knot K, and and are the electrophoretic run times. The width of the Gaussians is set to be proportional to the SD of the velocities. The resulting spots can be seen as the in silico analog of the ones observed in gel electrophoretic experiments. Note that the combination of a monotonic behavior along the weak field direction with a nonmonotonic one along the stronger field gives rise to the arc-shaped distribution of the spots characteristic of 2D electrophoresis experiments run either on knotted configurations or on supercoiled plasmids (4) (see Fig. 2D).
It is interesting to ask whether one can observe the electrophoretic arc also in simulations where the gel is a regular cubic mesh, i.e., a mesh with no dangling ends, as this has been, so far, the typical way to model an agarose gel (16). Remarkably, unlike the case of gel with dangling ends, also called “irregular” hereafter, no example of nonmonotonic behavior of the knot mobility is found for regular gels (for comparison, see Fig. 2C and Fig. S1). This result is in line with previous simulations based on lattice knots in regular gels (16) and persists for different field strengths ( V/cm) and gel pore sizes ( nm) (see Supporting Information). [We note that physical gels also have an inhomogeneous pore size; although considering this aspect will affect our results quantitatively, the common understanding is that the knot speed should depend monotonically on size (1). This is qualitatively different from the case of dangling ends, where the gel–polymer interactions strongly depend on topological complexity as well.] Hence our simulations strongly suggest that the causes for the nonmonotonic behavior, observed in the case of irregular gels, are to be sought in the interaction between the knots and the gel dangling ends.
Fig. S1.
(A and B) Ttrajectory and squared radius of gyration vs. time for some knotted DNA loops subject to weak (50 V/cm) (A) and moderate (150 V/cm) (B) electric fields and moving through an irregular gel, i.e., with dangling ends. C and D refer to the case in which the knots travel through a regular gel at weak and moderate electric fields, respectively. Note that, for high fields and in gel with dangling ends, the knotted loops are trapped (zero velocity) for a long time in states with large radius of gyration, suggesting an entangled or impalement state, whereas, in a regular gel, the difference between the trajectories at weak and moderate fields is very small. (E) The velocity of knotted polymers in regular gels, i.e., without dangling ends, displays a monotonic behavior as a function of the ACN. For dense enough gels ( nm), the contribution coming from the interaction with the structure is observed to be sufficient to recover the linear electrophoretic separation as a function of the ACN at weak fields ( V/cm). This is, however, not observed in the case of sparser gels ( nm), where we recover no electrophoretic separation (F). We observed a deviation from the linear trend only at stronger fields and denser gels ( V/cm, nm), although we never observed a field inversion or nonmonotonic behavior (G).
This conjecture is also supported by the fact that linear (open) DNA samples are frequently observed to migrate faster than covalently closed (unknotted) ones in gel electrophoresis experiments performed in both strong and weak fields (4, 6, 18, 29). This is in line with the outcome of a recent computer experiment probing the dynamics of linear and unknotted circular molecules through an irregular gel (20).
DNA Samples Become Severely Entangled with the Dangling Ends
Having established that the presence of dangling ends in gels severely affect the transport properties of the knotted DNA loops under moderate electric fields, it is natural to look at the possible mechanisms ruling this phenomenon.
The typical trajectories and average extension of some knotted loops as they move through a regular model gel and a gel with dangling ends are markedly different at moderate fields (see Fig. S1). In a regular gel, knots respond to the field, by shrinking their size so as to channel through the pores of the gel more efficiently. This mechanism, also known as “channeling,” in which polymers squeeze through the gel pores, has already been observed in previous works (30, 31), and it was previously conjectured to play a role in the nonmonotonic separation of DNA knots in gels, as more-complex knots could have a different ability in deforming their overall shape when squeezing through the pores (4). On the other hand, as discussed in DNA Knots Form an Electrophoretic Arc, we find that this behavior is not sufficient to explain the electrophoretic arc, as, for regular gels, we always observe a monotonic separation of the knots as a function of the ACN (see Fig. S1). Conversely, in the case of irregular gels, knotted loops are much more prone to entangle with one (or more) dangling ends (see Insets of Fig. 2C for some examples). These entangled states (or impalements) require some time to be unraveled, and this is the reason for the anomalously long pauses observed in the knot trajectories (see, in particular, Fig. S1). Clearly, as the DNA gets longer, impalements, which can either be parallel or perpendicular with respect the direction of the field, become progressively more likely. As a matter of fact, this could be one of the reasons why it is, in practice, unfeasible to perform efficient gel electrophoresis experiments with circular DNA longer than 10 kbp (32): At these sizes, impalements are so frequent that they may cause DNA breakage.
In analogy with the phenomenon of threading, which slows down the dynamics of unknotted loops either in a melt or in a gel (20, 33, 34), and that of “crawling” of knots around obstacles (35), it is reasonable to expect that more-complicated knots will take longer to disentangle themselves from an impalement. We argue that this mechanism, when competing with the reduced Stokes drag of more-complex knots in gels, is ultimately responsible for producing a nonmonotonic dependence as a function of their complexity, i.e., their ACN.
More-Complex Knots Have Smaller Size but Larger Entanglement Number
Given that impalement events are key factors in determining the mobility of DNA knots within gels with dangling ends, it is important to find a way to define and measure this entanglement. Impalement may occur with dangling ends oriented along several directions (see examples in Fig. 2C), but it is reasonable to expect that all these events involve a similar mechanism in which, i.e., one dangling end “pierces through” the knot.
To quantify the degree of knot–gel entanglement, we consider an equilibrated knot configuration in the gel, and project it on the plane perpendicular to the field direction. We then choose randomly a base point P, at a distance from the projection plane that is much bigger than the radius of gyration of the projected configuration, . Starting from P, we draw an arc that pierces only once the projection plane at a point, Q, chosen randomly, with uniform probability within a disk of radius and centered in the center of mass of the projected configuration. The arc and the plane define a semispace, and we close the path with a second arc connecting Q and P and living in the other semispace (see Fig. 3A). To assess whether this circular path interacts topologically with the knotted configuration, we compute the absolute value of the linking number, , between the circular path and the knot. Fig. 3 B and C shows the result of this procedure when applied to two different knotted loops. By averaging over several circular paths with different Q, and over different knot configurations, we define the AEN, , as the measure of the degree of entanglement between the knotted loops and the surrounding gel.
Fig. 3.
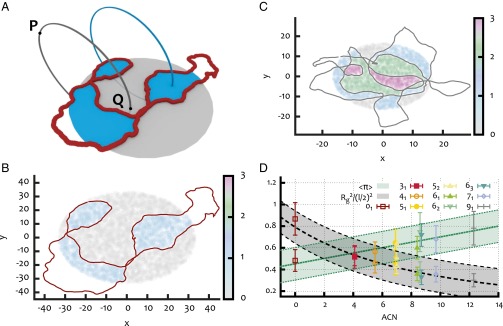
(A) Sketch of the procedure used to define the piercing, or entanglement number: For a given projection of the configuration, the crossings define a set of regions whose intersections with the disk of radius are highlighted in blue. Starting from different points P far away from the projections, closed paths (two in the example) that pierce the disk once at different locations Q are built at random. The absolute value of the linking number is then computed between the knot configuration and each closed path. The average over the set of closed paths is finally taken: This is the AEN. B and C show the results of the procedure described in A for a configuration with knot type (C) and for an unknotted configuration (B). The regions are colored according to the computed absolute value of the linking number (see color map at left). Note that for the case, there are regions of high (3), which are more prone to become entangled with the dangling ends of the gel. (D) The AEN and the mean squared radius of gyration divided by (l is the gel pore size) for different knot types classified in terms of ACN.
From Fig. 3D, we see that grows approximately linearly with can; as one would expect, more-complex knots can, on average, become more entangled with the surrounding irregular gel. It is interesting to compare this behavior with that of the mean squared radius of gyration normalized with respect to half the gel pore size (see Fig. 3D): Unlike the AEN, the average extension of the loop is, to a good approximation, inversely proportional to the ACN, i.e., to the knot complexity. This corresponds to the well-known fact that, for a given loop contour length, more-complex knots are on average less extended (5, 15) (see also the equilibrium configurations in Fig. 1).
The plots in Fig. 3D suggest a possible interpretation of the nonmonotonic mobility of the knots in irregular gels based on the interplay between the average size and the degree of entanglement with the gel. On one hand, more-complex knots, being smaller in size, experience less frequent collision with the gel and hence should travel more easily through it; this is just another variant of the Stokes friction argument discussed previously. On the other hand, once knot–gel collisions occur, more-complex knots experience a more intricate entanglement with the gel (higher values of AEN are more probable) that will take longer to unravel (5, 14, 16, 35).
The above argument suggests the existence of two time scales in the process: one is the time between two successive knot–gel collisions yielding a local entanglement; the other, , is the time needed by the knotted loop to fully disentangle from the impalement. The time scale increases as the knot average size decreases, and hence increases with knot complexity (ACN). In other words, more-complex knots experience, on average, less collisions with the gel than their simpler counterpart. The second time scale, , is instead an increasing function of (see Fig. 3D) and hence of the knot complexity (measured in terms of ACN). According to this picture, the slowest topoisomer in an irregular gel with a given lattice spacing will be the one with the best compromise between a high rate of collisions, and a sufficiently high value .
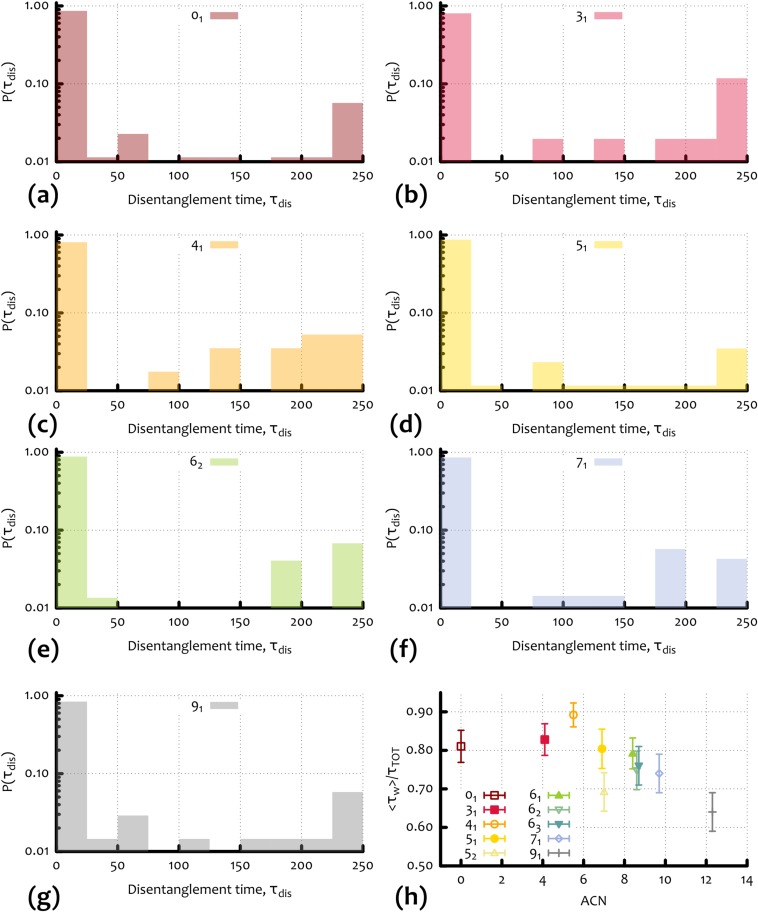
To investigate more quantitatively the dependence of and on the knot type (ACN), we analyze the trajectories of the knotted loops in the gel by computing (i) the average number of times a knot arrests its motion in the gel (entanglement event), , and (ii) the distribution of the duration of these entanglement events.
As specified in Supporting Information, the duration of the entanglement events can be identified as the time intervals where the spatial position of the center of mass of the configuration deviates significantly from the expected collision-free field-driven linear motion with speed .
As reported in Supporting Information (Fig. S2), the average fraction of time in which the knot is trapped, ( is the time of the full trajectory), is a nonmonotonic function of the ACN, in line with the result on the mobility under moderate field (Fig. 2B). In Fig. 3A, we show that the average number of entanglement events decreases with the knot complexity (i.e., ACN). On the other hand, the distribution of the duration of these events displays an intriguing bimodal shape, with two peaks occurring respectively at short and very long times (see Fig. S3). The peak at long times can be interpreted as the signature of head-on collisions with the gel, where the dangling ends involved are opposite to the direction of the knot motion. The resulting entanglement is, in this case, very difficult to unravel, especially in the presence of a strong electric field (see, for instance, Inset of Fig. 2 for the unknot). Nonetheless, whether or not we exclude from the statistic the entanglement events corresponding to the peak at long times, the characteristic disentanglement time turns out to increase (linearly) with the knot complexity, i.e., with ACN (see Fig. 4B).
Fig. S2.
(A–G) Waiting time distribution for different knot types and in units of simulation Brownian time : knot types 01 (A), 31 (B), 41 (C), 51 (D), 62 (E), 71 (F), and 91 (G). One can notice that the distribution shows peaks at short and large times that correspond to transverse or head-on interactions, respectively. (H) Total amount of time spent in an entangled state as a function of the ACN. This quantity reflects the fact that slower knots spend more time in entangled states (compare with Fig. 2).
Fig. S3.
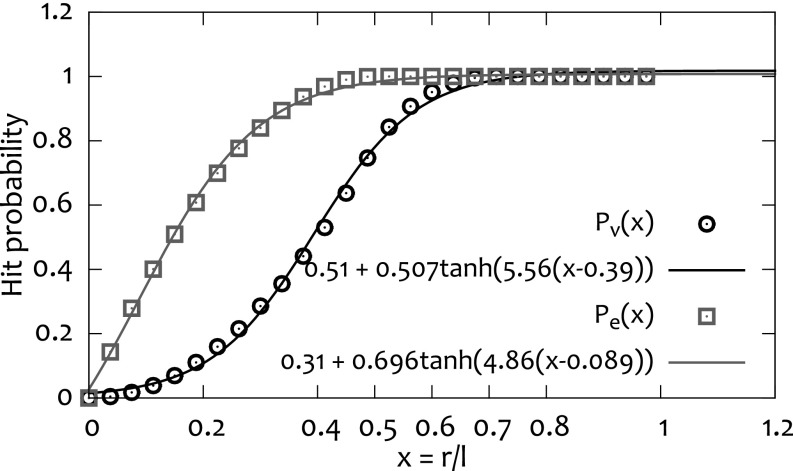
Probability for a circle of radius r drawn randomly on a square lattice with lattice spacing l to encircle a lattice vertex (, black circles) and to overlap over a lattice edge (, gray squares). The two quantities reach 1 for () and for (). The functions and parameters used to fit the data are also shown.
Fig. 4.
(A) Average number of events in which the knot is entangled with the surrounding gel (entanglement events) as a function of ACN. (B) Average disentanglement time as a function of ACN. In these estimates, only entanglement events with duration shorter than 200 are considered.
We assume that this bimodal shape is due to a shift in the energy barrier that the knots have to overcome to disentangle from the dangling ends. In particular, one can think of this process as an Arrhenius process, where the energy barrier is a function of the length (projected along the field direction) of the dangling end, the knot complexity, and, more importantly, the magnitude of the external field. When the external bias is too strong, disentanglement events are very rare, and all knots will end up being permanently entangled with the gel structure; on the other hand, when it is too weak, the typical disentanglement time is very short, and the dependence of as a function of the ACN dominates the motion of the polymers, reestablishing the usual linear relationship.
Random Walk Model with Topology-Dependent Rates Captures the Observed Nonmonotonic Behavior
As shown in DNA Knots Form an Electrophoretic Arc only in Irregular Gels, 2D electrophoresis experiments and Brownian dynamics simulations of knotted loops in irregular gels are in qualitative agreement in many aspects. In this section, we propose a simple model that reproduces the main findings of the simulations and furnishes a simple but accurate way to predict the arc shapes of the experimental patterns as a function both of the knot complexity and of the loop contour length.
In this model, we describe the knotted loop moving within the irregular gel as a biased random walk on a 1D lattice, i.e., a random walk that moves to the right (direction of the external field) unless it is trapped into an entangled state (due to impalement), with probability (see Supporting Information for more details). Once in the entangled state, the walker has to wait a given amount of time that is picked randomly from a bimodal distribution consisting of an exponential decay, modeling the short time disentanglement, and a smaller probability peak at large times, describing the long disentanglement time from a head-on collision (see Supporting Information for the details). In this simple description, the only relevant parameters are the hitting rate and the parameters characterizing the bimodal distribution of waiting (i.e., disentanglement) times.
Once the values of these parameters are set to reproduce the data reported in Fig. 3 (see also Supporting Information), the model can be used to predict the mobility of the electrophoretic arc as a function of ACN. As shown in Fig. 5, this procedure reproduces with remarkably good agreement the simulation data, and, in particular, it captures the physical mechanism leading to the nonmonotonic mobility at moderate field. Note that, as the random walker solely moves to the right, the field strength enters into the model only through the waiting times and the hitting rates.
Fig. 5.
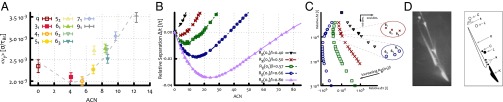
(A) Average speed along the direction of the moderate field from Fig. 2B. The dashed line is obtained from the biased continuous random walk model, and corresponds to the (shifted and rescaled) red curve in B. (B) Average relative separation (in units of lattice spacing over time) of the knots as a function of the ACN for different parameters, as predicted by the continuous random walk model. The gray dashed line in A is obtained by shifting the red curve in B by the value of and rescaling it by the free velocity . (C) Reconstruction of a 2D gel electrophoresis experiment from the data in B and zoom over the relative position of the family of six-crossings knots for two cases in which the minimum of the arc is at their left and their right. (D) Outcomes of a 2D gel electrophoresis experiments performed on P4 viral DNA with different lengths, respectively 4.7 (black) and 10 (white) kbp at equal agarose concentration (0.4%) [reprinted with permission from ref. 29 (Trigueros and Roca)].
More importantly, once the parameter values of the biased random walk model are set for a given pore size of the gel, , their values for a different pore size, , can be estimated from general arguments (see Supporting Information). We can therefore use this simplified model to predict the moderate field mobility and the shape of the electrophoretic arcs of DNA knots in gels of variable pore size, e.g., tuned via agarose concentration (36) or nanowire growth cycle (37).
The plots presented in Fig. 5B and Fig. S4 suggest that tighter gels give rise to more curved (or deeper) arcs where the slowest knot has a higher ACN with respect to sparser gels. Moreover, because the entanglement rate and the disentanglement time (both of these relative to the same quantities for the unknot) should depend only on the ratio between the knot extension and the gel pore size l, a similar trend should also be observed by increasing the DNA loop contour length by keeping fixed l (see Supporting Information). This is in qualitative agreement with experiments, as electrophoretic arcs are straighter for shorter DNA molecules (Fig. 5D). A further quantitative prediction we can draw from our arguments is that the relative position of the three six-crossing knots can be controlled by tuning the pore size (Fig. 5) of the gel. Indeed, the size of the pores determines whether the Stevedore’s knot is to the left or to the right of the minimum of the mobility curve: In the former case, will moves faster in the gel than the and knots (which, having higher can, also have higher AEN), whereas, in the latter case, it will move more slowly. This detailed prediction could be tested in future electrophoresis experiments with knotted DNA loops moving within different gels.
Fig. S4.
Average relative separation over time (in units of lattice spacing over time) of the knots as a function of the ACN obtained from the simple CTRW model described in Random Walk Model with Topology-Dependent Rates Captures the Observed Nonmonotonic Behavior. (A) For weak fields (for which the disentanglement time is quick ), the linear relationship is reestablished for , whereas, in the two limiting cases and , we do not observe a clear separation, as expected. (B) The nonmonotonic behavior of the separation is reestablished when a topology-dependent disentanglement time is introduced in the model. The typical electrophoretic arc crucially depends on the ratio . (See Biased Continuous-Time Random Walk Model for details).
Conclusions
We have studied the role of topology in the gel electrophoretic mobility of DNA knots by means of Brownian dynamics simulations and a minimal model of biased random walk. We showed that, when the knots are driven through a physical gel, i.e., one possessing dangling ends, the knots’ mobility, as a function of their ACN, depends on the strength of the external field.
At weak fields, we recover the well-known linear relationship between migrating speed and knot type; at stronger fields, we observe instead a nonmonotonic behavior. We argue that this puzzling feature, routinely observed in experiments but not yet fully explained, can be better understood by taking into account the topological interactions, or entanglements, of the knots with the irregularities of the surrounding gel. Although more-complex knots assume more-compact configurations, and hence smaller Stokes friction than simpler knots, they also experience more-complex entanglements with the gel and, hence, longer disentanglement times. These two competing effects give rise to the nonmonotonic speed of the knots observed in the experiments, a feature that, remarkably, is absent for knotted loops moving in a regular gel (i.e., no dangling ends). Although most of our simulations were performed with a rigid gel, we tested that the results are qualitatively unchanged for gels with flexible dangling ends (see Materials and Methods and Supporting Information and Fig. S5).
Fig. S5.
(A) Picture of the gel with flexible dangling ends (light gray) anchored to the rigid structure (dark gray). (B and C) Average velocity of some knots under weak (50 V/cm) (B) and moderate (150 V/cm) (C) field. (D) Snapshots (not to scale) of entanglement events of (Top) and (Bottom) knots corresponding to stalling points in their trajectories and large values of .
We also propose a model that describes the motion of knotted DNA loops as a biased continuous-time random walk. This model, although minimal, by focusing on the competition between Stokes friction and topological entanglements highlighted by the simulations, is able to predict the shape of electrophoretic patterns of DNA knots of different contour length observed in gels with tunable physical properties. In particular, we predict that, by changing the ratio between the radius of gyration of the unknot and the gel pore size, 2D gel electrophoresis experiments should lead to deep electrophoretic arcs for tight gels (or long knots), and shallow ones for sparse gels (or short knots).
We hope that our results will prompt further experimental and numerical verification of the role of topology in the anomalous electrophoretic mobility of knotted polymers and, consequently, suggest new and more accurate setups to separate biopolymers of different topology. Lastly, we highlight that it may be possible to understand the patterns of DNA molecules with different densities of supercoiling within the presented framework as a similar competition between loop size and loop–gel interactions may be responsible for their characteristic behavior.
Materials and Methods
Double-stranded (ds) and nicked, i.e., torsionally relaxed, DNA (dsDNA) knots are modeled as closed and knotted semiflexible bead-spring chains (38), with beads of diameter nm, which reflects the thickness of hydrated B-DNA near physiological conditions (39). The persistence length is set to nm, and the chosen contour length corresponds to DNA loops of length kbp μm.
The gel is modeled as an imperfect and rigid cubic mesh, with lattice spacing nm compatible with the average pore size of agarose gels at 5% and artificial gels made of solid nanowires (36, 37) (for more details on the model and comparison with the case of flexible dangling ends, see Supporting Information). The irregularities, or dangling ends, of the gel are created by starting from a regular cubic mesh and then halving some of the edges randomly, with probability . Although this probability is chosen arbitrarily, it is possible to map it to a real value of disorder found in an agarose gel at a given concentration by comparing the mobility of linear and ring polymers running through it, similarly to what was done in ref. 20. The edges of the mesh are discretized with beads of size nm, which is compatible with the observed diameter of agarose bundles (36, 40, 41). For simplicity and computational efficiency, we model the gel as a static mesh, meaning that the mesh structure is not deforming under either thermal of mechanical strains. This is an approximation for an agarose gel, whose bundles are generally, at the concentrations used in gel electrophoresis, found to be made of tens of fibers whose persistence length has been observed to be around nm (40). In light of this, a conservative estimation of the persistence length of an agarose bundle is comparable with that of DNA, i.e., nm (this assumes weak attraction between the fibers; see Supporting Information). In this case, whose analysis is detailed in Supporting Information, we do not observe significant deviations from the results presented here in DNA Knots Form an Electrophoretic Arc only in Irregular Gels. It is also worth noticing that this perfectly rigid environment closely resembles artificial gels made of solid nanowires (37), which possess a much higher Young modulus and have been found to be optimal media for gel electrophoresis experiments.
The external field is modeled as a force acting on each bead forming the polymers. Assuming that, in physiological conditions, half of the charges from the phosphate groups are screened by counter ions (42), one can think that each bead ( nm bp) contains a total charge of , where is the electron charge. Within this assumption, we can map the external force applied onto each bead to an effective electric field . Although this mapping is a crude approximation of the Coulomb interaction between the charged DNA, the ions in solution, and the applied electric field, we find that we can recover a weak field behavior of the knotted samples, i.e., linear increase of the speed as a function of their ACN, up to V/cm, which is roughly comparable with the field intensity used in experiments. In this work, we used field intensities in the range from V/cm to V/cm.
The ACNs used in this work were obtained from ref. 43, where the authors computed the ACN corresponding to Möbius energy minimizing knotted configurations. The thermally averaged ACN of the samples used in this work has been computed from equilibrated configurations and has been found to be in a one-to-one correspondence to the values in ref. 43, confirming the linear relationship between the ACN of ideal and thermally agitated configurations (17).
The hydrodynamics is here considered only implicitly, as is customary for Brownian dynamics simulations. This means that the polymers do not feel one another via hydrodynamical interactions but are subject to thermal fluctuations due to a surrounding bath at fixed temperature T (see Supporting Information for more details).
The simulation time scale is given in terms of the Brownian time, which corresponds to the time taken by a bead of size σ to diffuse its own size, i.e., , where is the diffusion coefficient of one bead and cP (centipoise) is the solution (water) viscosity. From this, we obtain ns.
Model and Computational Details
Nicked DNA knotted loops are modeled as coarse-grained bead-and-spring circular chains with a knot manually tied in. Let and be, respectively, the position of the center of the ith bead and the vector of length between beads i and j.
The connectivity of the chain is treated within the finitely extensible nonlinear elastic model (38) with potential energy,
for and , otherwise; here we chose σ and , and the thermal energy is set to ε. The bending rigidity of the chain is captured with a standard Kratky–Porod potential,
where nm is the known Kuhn length of unconstrained DNA. The steric interaction between beads belonging to the polymers or the gel is taken into account by a truncated and shifted Lennard–Jones potential
where is the Heaviside function and can be, depending on the case, (diameter of the chain beads) and σ where is the diameter of the beads forming the gel. Notice that steric interactions between beads of the gel are excluded from the computation because we consider the gel as a static mesh. This mimics artificial gels made of solid nanowires, which have Young modulus times larger than that of agarose (37).
Denoting by U the total potential energy, the dynamic of the beads forming the rings is described by the following Langevin equation:
| [S1] |
where ξ is the friction coefficient and η is the stochastic delta-correlated noise. The variance of each Cartesian component of the noise, , satisfies the usual fluctuation dissipation relationship .
As customary (38), we set , with and the Brownian time , with as the characteristic simulation time step. From the Stokes friction coefficient of spherical beads of diameters σ, we have , where is the solution viscosity. By using the nominal water viscosity, and setting K and nm, one has ns. Note that, being the gel structure static for all times, no evolution equations for the beads belonging to the mesh are considered. The numerical integration of Eq. S1 is performed by using a standard velocity Verlet algorithm with time step ns and is implemented in the Large-scale Atomic/Molecular Massively Parallel Simulator (LAMMPS) engine.
The whole system is contained within a box of linear dimension with periodic boundary conditions in all three directions. The irregularities of a physical gel are created by starting from a regular cubic mesh and then halving some of the edges randomly, with probability . The lattice spacing is set to nm, which is typical for an agarose gel at 5% (36), and the edges of the mesh are discretized with beads of size nm, again compatible with the size of the agarose bundles (36, 40).
By considering the beads as cylinders with height and diameter equal to σ, the system volume fraction results , much smaller than the value at which the chains start to overlap (). In other words, the systems are in the dilute limit, and interchain interactions occur rarely in the simulations.
The starting point of the various simulations is a configuration in which simple knotted configurations are placed outside the box. We then slowly pull the rings inside the gel structure, avoiding any impalement. Finally, we place the boundaries of the simulation box so as to match the boundaries of the gel structure and impose periodicity along all of the three coordinate directions. To allow the equilibration of the system from this initial state, we first run time steps, which are disregarded before the external force is switched on. The mean and SE of various properties, as the mean displacement along , are calculated by averaging over the rings in the system and over different runs starting from different (equilibrated) initial conditions.
The magnitude of the force f acting on the beads is expressed as a multiple of the system units . The force acting on the beads can therefore be expressed as the resultant of an electric field kV/cm. In this work, we have used forces f in the range between and 5 , which can then be mapped to electric fields roughly between 1.25 V/cm and 625 V/cm, compatible with the values used in standard DNA gel electrophoresis (4, 12, 21, 22).
We compute the mobility of knotted polymers by measuring the center of mass displacement along the direction of the applied field. In Fig. S1, we show single example trajectories of the knots and their relative change of radius of gyration during in silico gel electrophoresis experiments. In Fig. S1, we also compare trajectories and speed of knots traveling in regular and irregular gels. As one can notice, whereas, in irregular gels (Fig. S1 A and B), the motion of the knots under weak (50 V/cm) and moderate (150 V/cm) fields displays a rather different behavior, in regular gels (Fig. S1 C and D), knots that are driven by the same external fields display similar trajectories. In particular, we do not observe a field inversion at any field or gel density (Fig. S1 E–G).
Role of Hydrodynamics
The Brownian dynamics scheme allows us to introduce an implicit solvent, i.e., there is no explicit hydrodynamics taken into account during the simulations. We made this choice assuming that, in the case of dense gels, the contribution coming from hydrodynamics would be negligible compared with the interactions of the polymers with the environment. This is confirmed in Fig. S1, where we show the linearly increasing speed of knots traveling through a regular gel at weak and strong fields. In both cases, even without the presence of hydrodynamics or rescaling, we recover the expected linear relationship between speed and ACN. In ref. 16, the authors rescaled the final velocities of the knots by using the Kirkwood–Risenman formula, thereby accounting for hydrodynamics. In this work, we observed that such rescaling does not affect the final functional form of the results; consequently, we did not introduce such rescaling. We argue that the contribution from hydrodynamics becomes relevant when sparser gels are considered. In this case, we observed that the rescaling operated in ref. 16 is necessary to recover the experimental observations, as no electrophoretic separation is observed (see Fig. S1F).
Waiting Times
To quantify the time taken by the rings to disentangle from the impalements, we analyze the single trajectories (reported, for example, in Fig. S1) and compute the amount of time each knot is moving slower than it would if it were free, i.e., . From this, we can quantify the total amount of time each knot is stuck in an entangled state. This is found to be a nonmonotonous function of the ACN (see Fig. S2H) and is in line with the nonmonotonic average speed of the knots and the relative separation in gel electrophoresis experiments as a function of their ACN.
Each time a knot is stalled, it takes a certain amount of time to reestablish its motion. We report the distribution of these waiting times () in Fig. S2 A–G for several knots. As one can notice, the distribution is bimodal, i.e., shows two distinct peaks at short and long times. We interpret the peak at short time scales as transversal impalements or crawling around the gel structure, whereas the peak at long times is interpreted as the fact that, sometimes, knots interact via a head-on collision with the gel open strands. This immobilizes the knots for a long time, because the only way to reestablish the motion is by moving against the field for a length of at least half lattice spacing.
Biased Continuous-Time Random Walk Model
Here we detail the biased continuous-time random walk (CTRW) model, whose results are reported in Random Walk Model with Topology-Dependent Rates Captures the Observed Nonmonotonic Behavior.
We start by noticing that the simulations suggest the existence of two important time scales in the dynamics: and , respectively regulating the frequency of entangling events and the time required to disentangle from the impalements with the dangling ends. First, we address the situation in which . In this case, the knots disentangle quickly, and we can think of the whole process as random walks biased in the opposite (the DNA is negatively charge) direction of the field. Due to topological interactions with the gel, the biased random walkers eventually stop with a rate . We expect that this rate should be described by the probability of a circle of radius r to overlap onto an edge of 2D square mesh with lattice spacing l, i.e.,
| [S2] |
where . Note that this rate is normalized with respect to the empirical value observed in the Brownian dynamics simulations for the unknot () at weak fields.
We can obtain the value of as a function of the ratio , with l as the gel lattice spacing from Fig. S2, where we simulated the deposition of a circle of radius r onto a 2D mesh with lattice spacing l and calculated the probability of overlapping over a strand [] or to encircle a vertex [] of the grid.
The knots moving in the gel are therefore viewed as random walkers on a lattice. They can jump one site to their right (broadly, this corresponds to one unit cell of the gel), or are required to stop for one time step (because ) with rate . This is equivalent to a Poisson process whose probability of getting entangled after t time steps is given by
| [S3] |
where we stress the dependence of on the knot type via its size . The average time between interactions is given by , and the average number of stops on a time t is . The relative separation between two knots can be expressed as
| [S4] |
where is the velocity of the knots when no interactions occur (when hydrodynamics is negligible this is the same for all knots), t is the observation time, and . From this, it is clear that the separation between knots and is proportional to the difference of their entanglement rates, as expected. Given that our model relies on the hitting probability between a knot and its environment, it is clear that, if the knot size is either much larger or much smaller than the gel lattice spacing, the electrophoretic separation is not as good as in the case where the two are comparable. Within our simple model, we recover good linear relationship within the range , meaning that short samples (or large gel pores compared with the gyration radius of the knots) work better than small pores (or very large ) for the electrophoretic separation at weak fields (32) (see Fig. S4A). This is compatible with the fact that it is often impractical to perform gel electrophoresis with very large samples. In fact, for other cases outside this range, we observe essentially no spatial separation of the knots (see Fig. S4A).
We now introduce a topology-dependent disentanglement time: Every time that the Random Walker undergoes a “stop,” we require that it has to wait an amount of time that increases proportionally to its AEN (see in Fig. 3). We pick the disentanglement time from an exponential distribution with characteristic time given by the empirical one observed in the molecular dynamics (MD) simulations (see Fig. 4), i.e.,
| [S5] |
where r is a random number and . As observed in More-Complex Knots Have Smaller Size but Larger Entanglement Number, the disentanglement time is expected to be a function of , i.e., to increase linearly with the ACN. We therefore use
| [S6] |
where is an empirical parameter fitted from the simulations and is the empirical average disentanglement time of the unknot. In addition, long waiting times, which are typical of head-on impalements, are taken into account by adding a small probability (, compatible with the bimodal distribution in Fig. 4) and conditioned to the fact that an entanglement event happened. For this, we set . Thus, the average disentanglement time from a head-on impalement is still knot-dependent but is much longer than any characteristic disentanglement time for other types of entanglements.
Within this model, we recover the electrophoretic arc in Fig. S4B. In addition, the shape of the arc can be finely tuned to obtain different depths of the arc and different slowest knots. This is mainly controlled via the ratio (we here assume that the external field is neither too weak or too strong). In Fig. 5, we show that, within this model, we can accurately recover the electrophoretic speed of the knots observed in the MD simulations by shifting the curve obtained with the CTRW model setting (as in the MD simulation) to the observed speed of the unknot and by rescaling it by the free speed at which the knots travel between two planes of the gel, i.e., two lattice sites in the CTRW model. It is worth noting also that this model allows us to predict the mobility of knots that were not probed by Brownian dynamics, by making use of the empirical functional forms of and derived from these simulations. It is also worth stressing that the only real free parameter of this model is the lattice spacing l, whereas the value of , , and are input parameters needed to calibrate the model to a target case.
Gel with Flexible Dangling Ends
Although the assumption that the gel is perfectly rigid is only an approximation for agarose gels, several experiments reported values for the persistence length of single agarose fibers in the range of nm; in particular, ref. 40 reports nm (the same work also presents evidence of the presence of dangling ends in the gel). Furthermore, each agarose bundle (or “fibril”) is formed by a number of fibers, with ranging between 10 and 20 (36, 40), and has a diameter nm (41). The persistence length of a full fibril might depend linearly or quadratically on (depending on the structure of the bundle and strength of interfiber interactions; see ref. 44). Therefore, a conservative estimate of the persistence length of an agarose bundle is attained if a linear scaling is assumed (corresponding to weak attractive interactions between the fibers (see ref. 44) leading to nm. To probe the effect of fibers’ flexibility on the entanglement/disentanglement process experienced by the knots traveling through the gel, we therefore modify the gel structure to accommodate flexible dangling ends (see Fig. S5A) described as semiflexible polymers with persistence length equal to that of dsDNA, and anchored to cross-links that are still modeled as rigid and static. This choice corresponds to flexible agarose bundles clamped at right angles at crosslinks, and avoids the unphysical scenario in which the moving molecule would drag the gel along. [The simulations in Fig. S5 consider flexible bundles with fixed angles at cross-link, i.e., the clamping at the cross-links is infinitely strong. For the case of the unknot, we checked that replacing this right-angle constraint with a soft angular potential keeps the dynamics qualitatively unchanged (we still observe entanglements or impalements).] As one can see from Fig. S5 B and C, the qualitative behavior of knots dynamics does not change with respect to the fully rigid gel. In particular, as soon as the external electric field assumes moderate values, the nonmonotonic behavior of the average velocity is recovered. In Fig. S5, we also show some snapshots of knots with relatively large values of (instantaneous) that become entangled with the flexible dangling ends; correspondingly, their trajectories stall. From the above analysis, we conclude that, although adding flexibility to the gel network might change the numerical values of, for instance, the disentanglement time of the knots, the qualitative nonmonotonic response as a function of their ACN, when driven by a moderate field, is not substantially changed.
Acknowledgments
D. Michieletto acknowledges support from the Complexity Science Doctoral Training Centre at the University of Warwick with funding provided by the Engineering and Physical Sciences Research Council (EPSRC) (EP/E501311). The computing facilities were provided by the Centre for Scientific Computing of the University of Warwick with support from the Science Research Investment Fund. D. Marenduzzo thanks EPSRC Grant EP/I034661/1 for support. E.O. acknowledges support from the Italian Ministry of Education Grant PRIN 2010HXAW77.
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1506907112/-/DCSupplemental.
References
- 1.Calladine CR, Drew H, Luisi FB, Travers AA. Understanding DNA: The Molecule and How It Works. Elsevier; New York: 1997. [Google Scholar]
- 2.Bates A, Maxwell A. DNA Topology. Oxford Univ Press; New York: 2005. [Google Scholar]
- 3.Olavarrieta L, et al. Supercoiling, knotting and replication fork reversal in partially replicated plasmids. Nucleic Acids Res. 2002;30(3):656–666. doi: 10.1093/nar/30.3.656. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Cebrián J, et al. Electrophoretic mobility of supercoiled, catenated and knotted DNA molecules. Nucleic Acids Res. 2014;43(4):e24. doi: 10.1093/nar/gku1255. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Stasiak A, Katritch V, Bednar J, Michoud D, Dubochet J. Electrophoretic mobility of DNA knots. Nature. 1996;384(6605):122. doi: 10.1038/384122a0. [DOI] [PubMed] [Google Scholar]
- 6.Arsuaga J, et al. DNA knots reveal a chiral organization of DNA in phage capsids. Proc Natl Acad Sci USA. 2005;102(26):9165–9169. doi: 10.1073/pnas.0409323102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.de Gennes PG. Scaling Concepts in Polymer Physics. Cornell Univ Press; Ithaca, NY: 1979. [Google Scholar]
- 8.Rubinstein M. Discretized model of entangled-polymer dynamics. Phys Rev Lett. 1987;59(17):1946–1949. doi: 10.1103/PhysRevLett.59.1946. [DOI] [PubMed] [Google Scholar]
- 9.Duke TA. Tube model of field-inversion electrophoresis. Phys Rev Lett. 1989;62(24):2877–2880. doi: 10.1103/PhysRevLett.62.2877. [DOI] [PubMed] [Google Scholar]
- 10.Viovy JL, Duke T. DNA electrophoresis in polymer solutions: Ogston sieving, reptation and constraint release. Electrophoresis. 1993;14(4):322–329. doi: 10.1002/elps.1150140155. [DOI] [PubMed] [Google Scholar]
- 11.Barkema GT, Marko JF, Widom B. Electrophoresis of charged polymers: Simulation and scaling in a lattice model of reptation. Phys Rev E Stat Phys Plasmas Fluids Relat Interdiscip Topics. 1994;49(6):5303–5309. doi: 10.1103/physreve.49.5303. [DOI] [PubMed] [Google Scholar]
- 12.Viovy J. Electrophoresis of DNA and other polyelectrolytes: Physical mechanisms. Rev Mod Phys. 2000;72(3):813–872. [Google Scholar]
- 13.Vologodskii AV, et al. Sedimentation and electrophoretic migration of DNA knots and catenanes. J Mol Biol. 1998;278(1):1–3. doi: 10.1006/jmbi.1998.1696. [DOI] [PubMed] [Google Scholar]
- 14.Weber C, Carlen M, Dietler G, Rawdon EJ, Stasiak A. Sedimentation of macroscopic rigid knots and its relation to gel electrophoretic mobility of DNA knots. Sci Rep. 2013;3:1091. doi: 10.1038/srep01091. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Piili J, Marenduzzo D, Kaski K, Linna RP. Sedimentation of knotted polymers. Phys Rev E Stat Nonlin Soft Matter Phys. 2013;87(1):012728. doi: 10.1103/PhysRevE.87.012728. [DOI] [PubMed] [Google Scholar]
- 16.Weber C, Stasiak A, De Los Rios P, Dietler G. Numerical simulation of gel electrophoresis of DNA knots in weak and strong electric fields. Biophys J. 2006;90(9):3100–3105. doi: 10.1529/biophysj.105.070128. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Katritch V, et al. Geometry and physics of knots. Nature. 1996;384:142–145. [Google Scholar]
- 18.Trigueros S, Arsuaga J, Vazquez ME, Sumners DW, Roca J. Novel display of knotted DNA molecules by two-dimensional gel electrophoresis. Nucleic Acids Res. 2001;29(13):E67. doi: 10.1093/nar/29.13.e67. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Arsuaga J, Vázquez M, Trigueros S, Sumners D, Roca J. Knotting probability of DNA molecules confined in restricted volumes: DNA knotting in phage capsids. Proc Natl Acad Sci USA. 2002;99(8):5373–5377. doi: 10.1073/pnas.032095099. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Michieletto D, Baiesi M, Orlandini E, Turner MS. Rings in random environments: Sensing disorder through topology. Soft Matter. 2015;11(6):1100–1106. doi: 10.1039/c4sm02324b. [DOI] [PubMed] [Google Scholar]
- 21.Mickel S, Arena V, Jr, Bauer W. Physical properties and gel electrophoresis behavior of R12-derived plasmid DNAs. Nucleic Acids Res. 1977;4(5):1465–1482. doi: 10.1093/nar/4.5.1465. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Levene SD, Zimm BH. Separations of open-circular DNA using pulsed-field electrophoresis. Proc Natl Acad Sci USA. 1987;84(12):4054–4057. doi: 10.1073/pnas.84.12.4054. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Turmel C, Brassard E, Slater GW, Noolandi J. Molecular detrapping and band narrowing with high frequency modulation of pulsed field electrophoresis. Nucleic Acids Res. 1990;18(3):569–575. doi: 10.1093/nar/18.3.569. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Åkerman B, Cole KD. Electrophoretic capture of circular DNA in gels. Electrophoresis. 2002;23(16):2549–2561. doi: 10.1002/1522-2683(200208)23:16<2549::AID-ELPS2549>3.0.CO;2-Q. [DOI] [PubMed] [Google Scholar]
- 25.Cole KD, Åkerman B. The influence of agarose concentration in gels on the electrophoretic trapping of circular DNA. Sep Sci Technol. 2003;38(10):2121–2136. [Google Scholar]
- 26.Robertson RM, Smith DE. Strong effects of molecular topology on diffusion of entangled DNA molecules. Proc Natl Acad Sci USA. 2007;104(12):4824–4827. doi: 10.1073/pnas.0700137104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Stellwagen NC, Stellwagen E. Effect of the matrix on DNA electrophoretic mobility. J Chromatogr A. 2009;1216(10):1917–1929. doi: 10.1016/j.chroma.2008.11.090. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Adams CC. The Knot Book: An Elementary Introduction to the Mathematical Theory of Knots. Freeman; New York: 1994. [Google Scholar]
- 29.Trigueros S, Roca J. Production of highly knotted DNA by means of cosmid circularization inside phage capsids. BMC Biotechnol. 2007;7:94. doi: 10.1186/1472-6750-7-94. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Mohan A, Doyle PS. Stochastic modeling and simulation of DNA electrophoretic separation in a microfluidic obstacle array. Macromolecules. 2007;40(24):8794–8806. [Google Scholar]
- 31.Mohan A, Doyle PS. Effect of disorder on DNA electrophoresis in a microfluidic array of obstacles. Phys Rev E Stat Nonlin Soft Matter Phys. 2007;76(4 Pt 1):040903. doi: 10.1103/PhysRevE.76.040903. [DOI] [PubMed] [Google Scholar]
- 32.Dorfman KD. DNA electrophoresis in microfabricated devices. Rev Mod Phys. 2010;82(4):2903–2947. [Google Scholar]
- 33.Michieletto D, Marenduzzo D, Orlandini E, Alexander G, Turner M. Threading dynamics of ring polymers in a gel. ACS Macro Lett. 2014;3:255–259. doi: 10.1021/mz500060c. [DOI] [PubMed] [Google Scholar]
- 34.Michieletto D, Marenduzzo D, Orlandini E, Alexander GP, Turner MS. Dynamics of self-threading ring polymers in a gel. Soft Matter. 2014;10(32):5936–5944. doi: 10.1039/c4sm00619d. [DOI] [PubMed] [Google Scholar]
- 35.Weber C, De Los Rios P, Dietler G, Stasiak A. Simulations of electrophoretic collisions of DNA knots with gel obstacles. J Phys Condens Matter. 2006;18(14):S161–S171. [Google Scholar]
- 36.Pernodet N, Maaloum M, Tinland B. Pore size of agarose gels by atomic force microscopy. Electrophoresis. 1997;18(1):55–58. doi: 10.1002/elps.1150180111. [DOI] [PubMed] [Google Scholar]
- 37.Rahong S, et al. Ultrafast and wide range analysis of DNA molecules using rigid network structure of solid nanowires. Sci Rep. 2014;4:5252. doi: 10.1038/srep05252. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Kremer K, Grest GS. Dynamics of entangled linear polymer melts: A molecular-dynamics simulation. J Chem Phys. 1990;92(8):5057. [Google Scholar]
- 39.Rybenkov VV, Cozzarelli NR, Vologodskii AV. Probability of DNA knotting and the effective diameter of the DNA double helix. Proc Natl Acad Sci USA. 1993;90(11):5307–5311. doi: 10.1073/pnas.90.11.5307. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Guenet JM, Rochas C. Agarose sols and gels revisited. Macromol Symp. 2006;242(1):65–70. [Google Scholar]
- 41.Sugiyama J, Rochas C, Turquois T, Taravel F, Chanzy H. Direct imaging of polysaccharide aggregates in frozen aqueous dilute systems. Carbohydr Polym. 1994;23(4):261–264. [Google Scholar]
- 42.Maffeo C, et al. DNA–DNA interactions in tight supercoils are described by a small effective charge density. Phys Rev Lett. 2010;105(15):158101. doi: 10.1103/PhysRevLett.105.158101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Kusner R, Sullivan J. Möbius energies for knots and links, surfaces and submanifolds. In: Kazez WH, editor. Geometric Topology: Proceedings of the 1993 Georgia International Topology Conference. Am Math Soc; Cambridge, MA: 1994. pp. 570–604. [Google Scholar]
- 44.Mogilner A, Rubinstein B. The physics of filopodial protrusion. Biophys J. 2005;89(2):782–795. doi: 10.1529/biophysj.104.056515. [DOI] [PMC free article] [PubMed] [Google Scholar]