Figure 4.

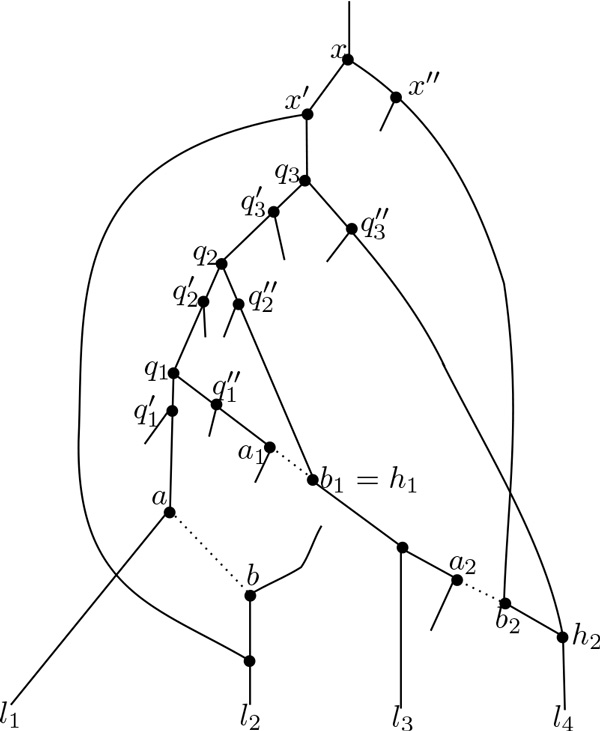
An illustration for the proof of Lemma 7. In this example: L = {l₁, l₂, l₃, l₄}, Q = {q₁, q₂, q₃}, L^* = {l₁, l₃, l₄}, L₃ = {l₄}, L₂ = {l₃}, and L₁ = ∅. For i = 1, let l(q₁) = l₃; thus, we have c(1) = 2 and the path p₁ starts from q₁, passes through $q_{\mathsf{\text{1}}}^{″}$, b₁ to l₃, while the path $p_1^{\prime }$ starts from q₂, passes through $q_2^{″}$, b₁ to l₃. In this case, we have h₁ = b₁. For i = 2, let l(q₂) = l₃; thus we have c(2) = 3 and the path p₂ starts from q₂, passes through $q_2^{″}$, b₁, b₂, h₂ to l₄, while the path $p_2^{\prime }$ starts from q₃ passes through $q_3^{″}$ to l₄. Let x be a node in ${\mathcal{M}}_{N^{\prime }}\left(L\right)$, then x is also in ${\mathcal{M}}_{N^{″}}\left(L\right)$ where N" is obtained from N' by removing all edges (a_i, b_i).