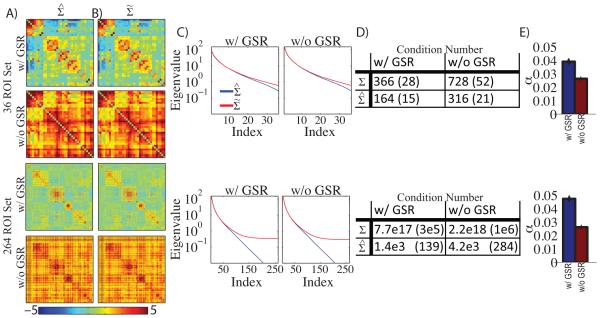
Figure 1. Matrix conditioning significantly improves the condition number of BOLD covariance matrices.

A: BOLD covariance matrices (Σ) calculated in the 36 and 264 ROI set with and without global signal regression (GSR). Matrices with GSR exhibit familiar block organization representing resting-state networks (RSNs). Matrices without GSR exhibit similar organization biased towards positive values. B: Conditioned BOLD covariance matrices ($\widehat{\Sigma }$) in the same configuration as A. Notably, there is no visual difference between matrices in A and B. C: Mean eigenspectra of matrices in A and B. The blue line indicates the eigenspectra corresponding to Σ and the red lines indicates the eigenspectra corresponding to $\widehat{\Sigma }$. The eigenvalues of Σ decay towards zero but the eigenvalues of $\widehat{\Sigma }$ plateau at a non-zero constant. D: Quantification of matrix invertibility by mean condition number. The condition number is defined as the ratio of the largest eigenvalue to the smallest. E: mean shrinkage coefficient (α) in each ROI set with and without global signal regression. Error bars indicate standard error of the mean estimated across subjects.